Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Jahangir, Adnan; Dar, Adiya; Othman, Mohamed I. A.

doi:10.21595/jets.2021.22166

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 11 November 2021

Check for updates

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Adnan Jahangir¹

Adiya Dar²

Mohamed I. A. Othman³

^{1, 2}Department of Mathematics, COMSATS University Islamabad, Wah Campus, Islamabad, Pakistan

³Department of Mathematics, Faculty of Science, Zagazig University, P.O. Box 44519, Zagazig, Egypt

Corresponding Author:

Adnan Jahangir

Cite the article Download PDF

Downloads 515

CrossRef Citations 1

Abstract

In this paper, estimation is made to investigate the influence of thermal loading due to laser pulse on elastic waves. The material through which the waves are propagating is homogeneous and isotropic in nature. Heat conduction through the media is analyzed by the model proposed by dual-phase-lag theory (DPL). The governing non-dimensional equations are solved by using the approximated harmonic solution. The expression for the field variables is obtained generally and represented graphically for a particular medium.

1. Introduction

Very rapid thermal processes under the action of an ultra-short laser pulse are interesting from the standpoint of thermoelasticity because they require deformation fields and an analysis of the coupled temperature. This means that the laser pulse energy absorption results in a localized temperature increase, which causes thermal expansion and generates rapid movements in the structure elements, thus causing the rise in vibrations. These effects make materials susceptible to the diffusion of heat by conduction.

The ultra-short lasers are those with the pulse duration ranging from nanoseconds to femtoseconds. The high intensity, energy flux, and ultra-short duration laser beam have studied situations where very large thermal gradients or an ultra-high heating rate may exist on the boundaries, this in the case of ultra-short-pulsed laser heating [1, 2]. The microscopic two-step models that are parabolic and hyperbolic are useful for modifying the material as thin films. When a metal film is heated by a laser pulse, a thermoelastic wave is generated due to thermal expansion near the surface. The stress wave induced by pico and femtosecond laser pulses in a semi infinite metal by expressing the laser pulse energy as a Fourier series was studied by Wang and Xu [3]. The effect of rotation on a fiber-reinforced on the generalized magneto-thermoelasticity subject to thermal loading due to the laser pulse was studied by [4]. The effect of Thomson and initial stress in a thermo-porous elastic solid under G-N electromagnetic theory was discussed by [5]. The effect of the laser pulse on transient waves in a nonlocal thermoelastic medium under G-N theory was explained by [6].

A unified filed approach for heat conduction from macro to macro scales was investigated by [7]. A simplest thermoelasticity theory with microtemperatures that takes under consideration many new variables was presented by [8]. Quintanilla and Rache [9] pointed out a note on stability in dual-phase-lag heat conduction. The propagation of harmonic plane waves with assigned frequency by employing the thermoelasticity theory with DPL model was presented by [10]. The problems related with DPL model heat conduction model were considered by [11-13] and many others.

The heat conduction in materials with micro-temperatures was discussed by [14]. He has examined his theoretical results, with excellent agreement, by comparing them with the experimental data. The effect of initial stress and hall current on a magneto-thermoelastic porous medium with micro-temperatures was presented by [15]. The theory of heat conduction in micromorphic continua with micro-temperatures was developed by [16]. Some, boundary value problems of the linear theory of thermoelasticity with micro-temperatures for different structures with applications are constructed by many investigators. The propagation of Rayleigh waves in a microstretch thermoelastic half-space with microtemperatures in context of L-S [17] theory of thermoelasticity was presented by [18]. The effect of initial stress on a porous thermoelastic medium with micro-temperatures was discussed by [19]. The magneto-thermoelastic solid with micro-temperatures and voids was studied by [20]. The relaxation effects of the volume properties of electrically conducting viscoelastic material were explained by [21]. The effect of Thomson and thermal loading due to laser pulse in a magneto-thermoelastic porous medium with energy dissipation was studied by [22]. Othman and Abouelregal [23] explained the effect of pulsed laser radiation on a thermo-visco-elastic semi-infinite solid under two-temperature theory. The effect of laser pulse and gravity field on thermoelastic medium under Green-Naghdi theory was studied by [24].

In this chapter we have considered a special type of heat source responsible of wave generation in thermoelastic medium. We have designed a thermoelastic medium model and the material is a homogeneous isotropic heated by laser pulse. To analyze the problem and get the numerical solutions for the temperature distribution, displacement function, stress components, normal mode analysis method is used. Finally, the theoretical results obtained are represented graphically for particular medium.

2. Problem formulation and basic equations

We have considering a generalized homogeneous isotropic thermoelastic medium with micro temperature and without any body-force while laser pulse is considered as the heat source. The rectangular Cartesian coordinates $(x, y, z)$ are used to represent the geometry of the half-space medium $z \geq 0$ , with $z$ axis vertically into the medium. All the quantities in the problem will be in form of coordinates $x$ and $z$ and time $t$ as variable function.

The set of constitutive equations are:

1

\{\begin{array}{l} σ_{i j} = λ δ_{i j} e_{κ κ} + 2 μ e_{i j} - β θ δ_{i j}, \\ q_{i j} = - k_{4} w_{r, r} δ_{i j} - k_{5} w_{i, j} - k_{6} w_{j, i}, \\ Q_{i} = (K - k_{3}) θ_{, i} + (k_{1} - k_{2}) w_{i}, \\ q_{i} = K θ_{, i} + k_{1} w_{i}, \end{array}

where $Q$ is heat input on laser pulse effects on heat equation and is representing, heat input in form of beam or laser-pulse [1]. We suppose that all functions are differentiable and continuous in the defined domain:

2

Q = \frac{I_{0} γ^{*} t}{2 π r^{2} t_{0}^{2}} e x p (- \frac{x^{2}}{r^{2}} - \frac{t}{t_{0}}) + γ^{*} y,

where $I_{0}$ is heat absorbed $t_{0}$ is pulse rise, $r$ is radius of beam, $γ^{*}$ is depth of absorbing heat energy and with $t$ time variable. The system of governing equations can be represented as:

3

μ \nabla^{2} u + (λ + μ) \nabla (\nabla . u) - β \nabla θ = ρ \frac{\partial^{2} u}{\partial t^{2}},

4

k_{6} \nabla^{2} w + (k_{4} + k_{5}) \nabla (\nabla \cdot w) - k_{3} \nabla θ - k_{2} w - b \frac{\partial w}{\partial t} = 0,

5

(1 + τ_{Τ} \frac{\partial}{\partial t}) θ_{, i i} + \frac{k_{1}}{K} (\nabla \cdot w) = (1 + τ_{q} \frac{\partial}{\partial t}) (\frac{ρ c_{e}}{K} \frac{\partial θ}{\partial t} + \frac{β θ_{0}}{K} \frac{\partial e_{k k}}{\partial t} - \frac{ρ Q}{K}) .

Introducing the following variables to dimensionless the governing system of equation:

6

{x^{'}}_{i} = \frac{x_{i}}{l_{0}}, t^{'} = \frac{c_{1} t}{l_{0}}, u'_{i} = \frac{u_{i}}{l_{0}}, θ^{'} = \frac{θ}{θ_{0}}, {w^{'}}_{i} = w_{i} l_{0},

{τ^{'}}_{Τ} = \frac{c_{1}}{l_{0}} τ_{Τ}, τ_{q}^{'} = \frac{c_{1}}{l_{0}} τ_{q}, \nabla^{2} = \frac{1}{l_{0}^{2}} {\nabla'}^{2}, Q^{'} = \frac{l_{0} Q}{c_{1} θ_{0} C_{e}} .

where, $l_{0}$ is standard length and $c_{1}$ is the standard velocity given by $c_{1} = \sqrt{(λ + 2 μ / ρ)}$ . After non dimensional the governing equations can be represented as, (primes are dropped for simplicity):

7

α_{0} \nabla^{2} u + α_{1} \nabla (\nabla . u) - H \nabla θ = \frac{\partial^{2} u}{\partial t^{2}},

8

β_{0} \nabla^{2} w + β_{1} \nabla (\nabla \cdot w) - β_{2} \nabla θ - β_{3} w - β_{4} \frac{\partial w}{\partial t} = 0,

9

α_{2} (1 + τ_{Τ} \frac{\partial}{\partial t}) θ_{, i i} + α_{3} (\nabla \cdot w) = (1 + τ_{q} \frac{\partial}{\partial t}) (\frac{\partial θ}{\partial t} + α_{4} \frac{\partial e_{k k}}{\partial t} - Q),

where:

10

α_{0} = \frac{μ}{ρ c_{1}^{2}}, α_{1} = \frac{(λ + μ)}{ρ c_{1}^{2}}, α_{2} = \frac{K}{l_{0} ρ c_{e} c_{1}}, α_{3} = \frac{k_{1}}{l_{0} ρ θ_{0} c_{e} c_{1}}, α_{4} = \frac{β}{ρ c_{e}},

H = \frac{β^{'} θ_{0}}{ρ c_{1}^{2}}, β_{0} = \frac{k_{6}}{l_{0}^{3}}, β_{1} = \frac{(k_{4} + k_{5})}{l_{0}^{3}}, β_{2} = \frac{k_{3}}{l_{0}}, β_{3} = \frac{k_{2}}{l_{0}}, β_{4} = \frac{b}{l_{0}^{2}} .

Displacement and micro-temperature functions could be converted in terms of potential function by following expression [18]:

11

u_{1} = (\frac{\partial R}{\partial x} + \frac{\partial ψ}{\partial z}), u_{3} = (\frac{\partial R}{\partial z} - \frac{\partial ψ}{\partial x}), w = \nabla ν,

where, $R$ and $ν$ are scalar potentials functions, and vector potential is representing by $ψ$ . After some algebraic calculations the above equations become:

12

(α_{0} + α_{1}) \nabla^{2} R - H ϕ = \frac{\partial^{2} R}{\partial t^{2}},

13

α_{0} \nabla^{2} ψ = \frac{\partial^{2} ψ}{\partial t^{2}},

14

σ \nabla^{2} v - β_{2} ϕ - β_{3} v - β_{4} \frac{\partial v}{\partial t} = 0,

15

α_{2} (1 + τ_{Τ} \frac{\partial}{\partial t}) \nabla^{2} θ + α_{3} \nabla^{2} v - (1 + τ_{q} \frac{\partial}{\partial t}) (\frac{\partial θ}{\partial t} + α_{4} \nabla^{2} \frac{\partial R}{\partial t} - Q) = 0 .

2.1. Harmonic solution of the problem

Now let us consider that each field variable is propagating through the medium in terms of harmonic waves as:

16

{R, ϕ, v, ψ} (x, z, t) = {R^{*}, ϕ^{*}, v^{*}, ψ^{*}} (z) e x p (ω t + i a x),

where $ω$ is the angular frequency $i = \sqrt{- 1}$ , $a$ is the wave number in the $z$ -direction and $R^{*}$ , $ϕ^{*}$ , $v^{*}$ , $ψ^{*}$ are the amplitudes in the field quantity. By using Eq. (15) in Eqs. (11)-(14) can be represented as:

17

(α D^{2} + A_{1}) R^{*} - H θ^{*} = 0,

18

(α_{0} D^{2} + A_{3}) ψ^{*} = 0,

19

(σ D^{2} - A_{7}) v^{*} - β_{_{2}} θ^{*} = 0,

20

(α_{2} D^{2} π_{1} + A_{5}) θ^{*} + α_{3} (D^{2} - a^{2}) v^{*} + (- α_{4} D^{2} π_{2} + A_{6}) R^{*} = [- t Q_{0} - τ_{q} Q_{0} (1 - \frac{t}{t_{0}}) e x p (- ω t - i a x)],

where:

21

A_{1} = - α a^{2} - w^{2}, A_{3} = - α_{0} a^{2} - w^{2},

π_{1} = (1 + τ_{Τ} ω), π_{2} = (ω + τ_{q} ω^{2}), Q_{0} = \frac{I_{0} γ^{*}}{2 π r^{2} t_{0}^{2}} e x p (- \frac{x^{2}}{r^{2}} - \frac{t}{t_{0}} + γ^{*} z) .

For nontrivial solution the determinant of the above system of equations need to be zero, it implies:

22

[D^{6} - A D^{4} + B D^{2} - C] {θ^{*}, v^{*}, R^{*}} (z) = (L_{1}, L_{2}, L_{3}) f^{*} (x, t) e x p (γ^{*} z),

where:

A = - \frac{A_{1}}{g_{6}} - g_{8} + g_{9} - g_{10} + g_{21}, B = g_{11} - g_{12} - g_{13} - g_{14} + g_{15} + g_{16} + g_{17},

C = g_{18} + g_{19} + g_{20}, L_{1} = \frac{γ^{*^{4}}}{g_{2}} + \frac{A_{1} γ^{*^{2}}}{g_{2} g_{6}} + \frac{A_{7} γ^{*^{2}}}{g_{2} g_{3}} - \frac{A_{1} A_{7}}{g_{1}},

L_{2} = \frac{β_{2} γ^{*^{2}}}{g_{2} g_{3}} + \frac{A_{1} β_{2}}{g_{1}}, L_{3} = \frac{H γ^{*^{2}}}{g_{2} g_{6}} + \frac{H A_{7}}{g_{1}},

f^{*} (x, t) = \frac{I_{0} γ^{*}}{2 π r^{2} t_{0}^{2}} e x p (- \frac{x^{2}}{r^{2}} - \frac{t}{t_{0}}) [- t - τ_{q} e x p (ω t + i a x) + \frac{t}{t_{0}} e x p (ω t + i a x)],

g_{1} = α α_{2} π_{1} σ, g_{2} = α_{2} π_{1}, g_{3} = σ, g_{4} = α_{3} β_{2}, g_{5} = α_{4} π_{2} β,

g_{6} = α, g_{7} = α α_{2} π_{1}, g_{8} = \frac{A_{5}}{g_{2}}, g_{9} = \frac{A_{7}}{g_{3}}, g_{10} = \frac{g_{4}}{g_{2} g_{3}},

g_{11} = \frac{A_{1} g_{8}}{g_{6}}, g_{12} = \frac{A_{1} g_{9}}{g_{6}}, g_{13} = \frac{A_{5} A_{7}}{g_{7}}, g_{14} = g_{10} a^{2}, g_{15} = g_{10} A_{1},

g_{16} = \frac{A_{6} β}{g_{7}}, g_{17} = \frac{g_{5} A_{7}}{g_{1}}, g_{18} = \frac{A_{1} g_{7} g_{13}}{g_{1}}, g_{19} = \frac{g_{14}}{g_{1}},

g_{20} = \frac{A_{6} g_{16}}{g_{1}}, g_{21} = \frac{g_{5}}{g_{1}}, D = \frac{d}{d z} .

Now Eq. (22) can be factored as:

23

(D^{2} - k_{1}^{2}) (D^{2} - k_{2}^{2}) (D^{2} - k_{3}^{2}) θ^{*} (z) = L_{1} f^{*} (x, t) e x p (γ^{*} z) .

Whereas, the roots of characteristic equation are $k_{i}^{2}$ , $i = 1,2, 3$ . The general solution of the problem is given by:

24

θ (x, z, t) = \sum_{n = 1}^{3} M_{n} e x p (- k_{n} z + ω t + i a x) + N_{1} L_{1} f^{*} (x, t) e x p (γ^{*} z),

25

ψ (x, z, t) = M_{4} e x p (- k_{4} z + ω t + i a x),

26

v (x, z, t) = \sum_{n = 1}^{3} H_{1 n} M_{n} e x p (- k_{n} z + ω t + i a x) + N_{1} L_{2} f^{*} (x, t) e x p (γ^{*} z),

27

R (x, z, t) = \sum_{n = 1}^{3} H_{2 n} M_{n} e x p (- k_{n} z + ω t + i a x) + N_{1} L_{3} f^{*} (x, t) e x p (γ^{*} z),

where $k_{4}^{2} = - A_{3} / α_{0}$ are roots of the characteristic Eq. (23) and $M_{n}$ are some coefficients to be find:

28

N_{1} = \frac{1}{γ^{*^{6}} - A γ^{*^{4}} + B γ^{*^{2}} - C}, H_{1 n} = \frac{β_{2}}{(σ k_{n}^{2} - A_{7})}, H_{2 n} = \frac{H}{(σ k_{n}^{2} + A_{1})},

f^{*} (x, t) = \frac{I_{0} γ^{*}}{2 π r^{2} t_{0}^{2}} e x p (- \frac{x^{2}}{r^{2}} - \frac{t}{t_{0}}) [- t - τ_{q} + \frac{t}{t_{0}}] .

Using the relation of potential functions we get:

29

u_{1} = [\sum_{n = 1}^{3} i a M_{n} H_{2 n} e x p (- k_{n} z) - k_{4} M_{4} e x p (- k_{4} z)] e x p (i a x + ω t) - \frac{2 x}{r^{2}} N_{1} L_{3} f^{*} (x, t) e x p (γ^{*} z),

30

u_{3} = [\sum_{n = 1}^{3} (- k_{n}) M_{n} H_{2 n} e x p (- k_{n} z) - i a M_{4} e x p (- k_{4} z)] e x p (i a x + ω t) + γ^{*} N_{1} L_{3} f^{*} (x, t) e x p (γ^{*} z),

31

w_{1} = \sum_{n = 1}^{3} i a H_{1 n} M_{n} e x p (- k_{n} z + ω t + i a x) - (\frac{2 x}{r^{2}}) N_{1} L_{2} f^{*} (x, t) e x p (γ^{*} z),

32

w_{3} = \sum_{n = 1}^{3} - k_{n} H_{1 n} M_{n} e x p (- k_{n} z + ω t + i a x) + (γ^{*}) N_{1} L_{2} f^{*} (x, t) e x p (γ^{*} z) .

The components of stress are:

33

σ_{z z} = [\sum_{n = 1}^{3} M_{n} H_{5 n} e x p (- k_{n} z) + N_{7} M_{4} e x p (- k_{4} z)] e x p (i a x + ω t) + N_{8} f^{*} (x, t) e x p (γ^{*} z),

34

σ_{x z} = [\sum_{n = 1}^{3} M_{n} H_{3 n} e x p (- k_{n} z) + N_{2} M_{4} e x p (- k_{4} z)] e x p (i a x + ω t) + N_{3} f^{*} (x, t) e x p (γ^{*} z),

where:

35

H_{3 n} = - 2 i a α_{0} k_{n} H_{2 n}, N_{2} = α_{0} ({k_{4}}^{2} + a^{2}), N_{3} = \frac{- 4 x α_{0} γ^{*}}{r^{2}} L_{3} N_{1},

H_{5 n} = [α (k_{n}^{2} - a^{2}) - 2 i a μ k_{n}] H_{2 n} - β θ_{0},

N_{7} = 2 μ a^{2}, N_{8} = N_{1} [\frac{- 2 λ L_{3}}{r^{2}} + \frac{4 λ x^{2}}{r^{4}} L_{3} + λ L_{3} γ^{*^{2}} - \frac{4 x μ γ^{*}}{r^{2}} L_{3} - β θ_{0}] .

2.2. Boundary conditions

The boundary conditions assumed at the surface $z = 0$ to find the remaining unknown constants used in above exponential solution of the problem are,

1) Time dependent periodic force with magnitude $f (x, 0, t)$ is assumed to be acting normally on the medium, while tangentially the medium is considered as isolated from the surrounding:

36

σ_{z z} (x, 0, t) = f_{0} e x p (ω t + i a x),

37

σ_{x z} (x, 0, t) = 0,

where $f_{0}$ is an arbitrary constant function.

2) From condition on thermal boundary condition, the surface of half space is at some fixed temperature:

38

θ (x, 0, t) = θ_{0} e x p (ω t + i a x) .

3) Normal component of heat flux moment vector is zero:

39

q_{z z} = 0 .

By applying the above obtained solutions in boundary conditions, we get:

40

\sum_{n = 1}^{3} M_{n} H_{5 n} + N_{7} M_{4} = f_{0},

41

\sum_{n = 1}^{3} M_{n} H_{3 n} + N_{2} M_{4} = 0,

42

\sum_{n = 1}^{3} M_{n} = θ_{0},

43

\sum_{n = 1}^{3} π_{7 n} H_{1 n} M_{n} = 0,

where, $π_{7 n} = [k_{4} a^{2} + (k_{4} + k_{5} + k_{6}) k_{n}^{3}] .$

To find the values of $M_{n}$ , $n = 1,2, 3$ , and $M_{4}$ we will apply matrix inversion method on system of equations:

44

[\begin{array}{l} M_{1} \\ M_{2} \\ M_{3} \\ M_{4} \end{array}] = {[\begin{matrix} H_{51} & H_{52} & H_{53} & N_{7} \\ H_{31} & H_{32} & H_{33} & N_{2} \\ 1 & 1 & 1 & 0 \\ π_{71} H_{11} & π_{72} H_{12} & π_{73} H_{13} & 0 \end{matrix}]}^{- 1} [\begin{matrix} f_{0} \\ 0 \\ θ_{0} \\ 0 \end{matrix}] .

Hence, we obtain the solution of each field variable.

2.3. Numerical results and discussion

The evaluated theoretical results are computed numerically by using the relevant parameters for the case of magnesium crystal. The relevant physical values of elastic constants and micro-temperatures as [20]: $ρ =$ 1.74×10³ kgm^-3, $λ =$ 9.4×10¹⁰ Nm^-2, $μ =$ 4.0×10¹⁰ Nm^-2, $β =$ 7.779×10^-8 N, $C_{e} =$ 1.04×10³ NmKg^-1 K^-1, $θ_{0} =$ 0.298, $b =$ 0.15×10⁹ N.

The micro-temperature parameters are, $k_{1} =$ 0.0035 Ns^-1, $k_{2} =$ 0.045 Ns^-1, $k_{3} =$ 0.055 NK^-1 s^-1, $k_{4} =$ 0.064 Ns^-1 m², $k_{5} =$ 0.075 Ns^-1 m², $k_{6} =$ 0.096 Ns^-1 m².

The computations of figure (a) are carried out for different values of the time parameter $t,$ to see the variations because of different time for laser pulse while $t_{τ} =$ 0.015 sec and $t_{q} =$ 0.02 sec. In the figures (part-b) is representing the variations because of $t_{τ}$ and $t_{q}$ and $t =$ 0.1 sec. Graphical representation is made for low values for wave number $a =$ 0.001 cycle/secon the plane $x =$ 1. The non-dimensional field variables as, the temperature, displacement components, micro-temperature components, normal stress and tangential stress distribution functions are represented graphically for different values of time parameter $t .$

Fig. 1 depicts the behavior of heat propagating through the medium under different conditions of times. From part-a, it can be analyzed that the maximum value of the amplitude increases as the value of time $t$ increases. Part-b indicates the absolute value of the temperature gradient and heat fluxes are directly proportional to all the three-time lags. The curves converge to zero as the vertical distance from the surface increases indicating the waves to be surface waves in nature.

Fig. 1θ against z for different time

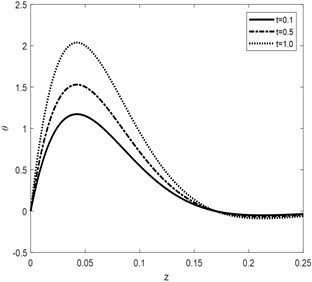
a)

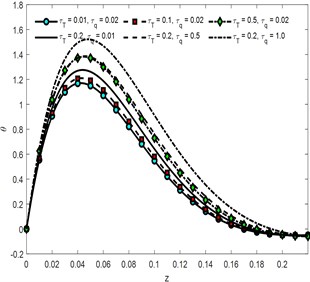
b)

Fig. 2u1 against depth for different values of time

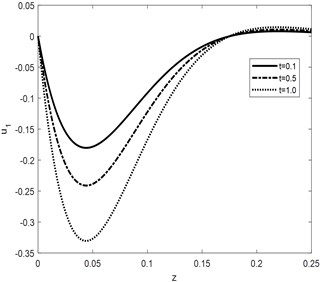
a)

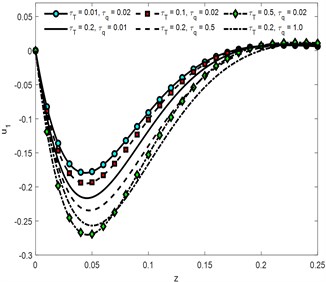
b)

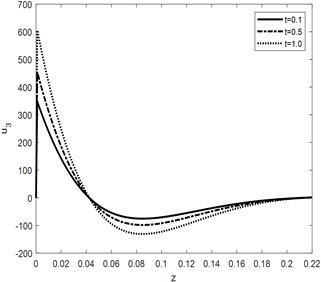
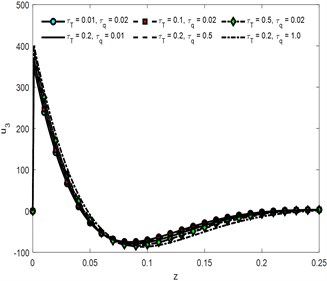
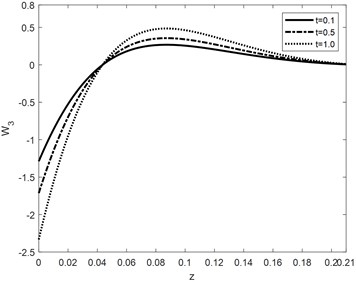
Fig. 3u3 against depth for different values of t

a)

b)

Fig. 2 represents the behavior of horizontal component of displacement against vertical component of distance. It can be analyzed that the absolute value of the curves increases by increasing the time parameter involved in the model of the system. Similarly, phase lags are directly proportional to the absolute value of the amplitude of wave propagating through the medium. Graphical analysis of vertical component of displacement is represented in Fig. 3.

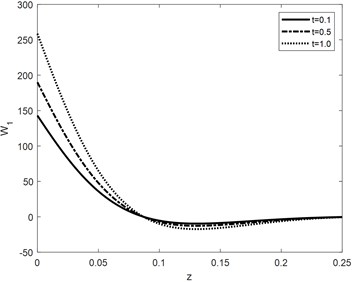
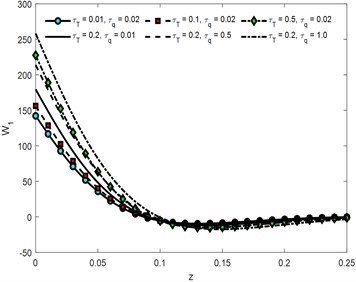
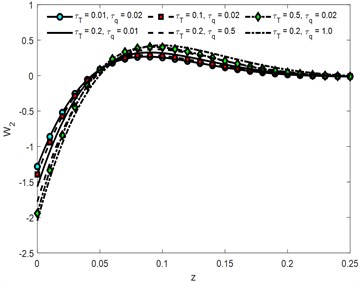
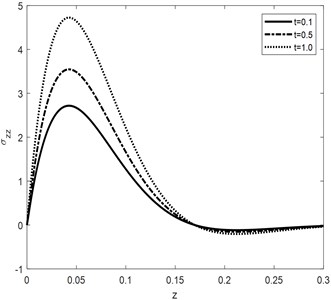
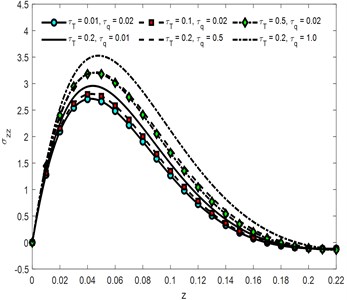
The curves for vertical components of displacement are responding to time parameter same as $u_{1}$ and the cases the curves for $t =$ 0.1 converge to zero first. Phase lags $τ_{T}$ and $τ_{q}$ are having decreasing effect for some initial values of vertical distance but for depth > 0.075 the behavior reversed. Convergence of curve toward zero reduces as the times increases. Micro-temperature components against vertical component of distance are shown in Fig. 4 and Fig. 5. Time parameter is having increasing effect on absolute values of the amplitude of waves generated because of non-dimensional components of micro-temperature. It can be analyzed that the convergence rate of the curve is inversely proportional to the times. Greater the value of time lag $τ_{q}$ higher the amplitude of the curve, it also reduces the convergence rate of the particle toward equilibrium. Similarly, the influence of $τ_{T}$ is directly proportional to the amplitude of waves propagating through the medium. The curves in context of $τ_{q} =$ 0.02, $τ_{T} =$ 0.01 damped to zero faster than all the other conditions. Variation in Normal component of stress distribution function against time parameter is graphically represented in Fig. 6. Over all curves are having increasing effect of stress wave. The amplitude increases for $0 \leq z \leq 0.042$ and decreasing for the other values of vertical component of distance. The curves for $t =$ 0.01 converge to zero earlier than the curves for higher value of time parameter.

Fig. 4Micro-temperature 1st component against different values of time

a)

b)

Fig. 5Micro-temperature 2nd component against different values of time

a)

b)

Propagation of shear stress along the material is presented in the Fig. 7. Just like all other field variables the tangential component of stress has the same response against time parameter of laser pulse. Influences of both the phase-lags $τ_{T}$ and $τ_{q}$ are directly proportional to the wave propagating through the medium. Highest amplitude is obtained for the value $τ_{T} =$ 0.2 and $τ_{q} =$ 1.0.

Fig. 6Normal stress σzz component against depth for different values of t

a)

b)

Fig. 7Tangential stress σzx component against depth for different values of t

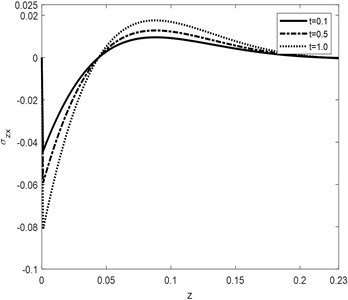
a)

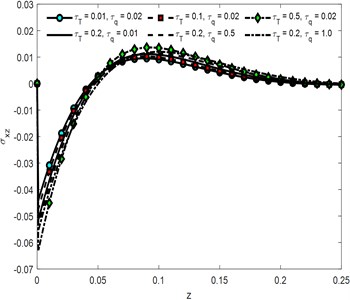
b)

3. Conclusions

Following are some main points which could be concluded after considering the solutions of the problem:

1) Harmonic solution used in Eq. (16) to find the solution of field variables gives analysis of surface waves propagating in the medium. All curves obtained are having non-zero values only in a bounded domain along depth of medium i.e., outside this domain the effects of the waves vanish or converge to zero.

2) The curves obtained during the case of non-dimensional temperature distribution function starts from same initial value depending on selection of $θ_{0}$ in boundary condition. Similarly curves for non-dimensional normal component of stress, and non-dimensional tangential stress starts from zero. These are fully agreement with the physical interpretation of boundary conditions.

3) Time parameter is having decreasing effect on the factor responsible for damping of wave.

4) The phase-lags $τ_{T}$ and $τ_{q}$ are increasing the amplitude of each wave propagating through the medium and having decreasing effect on the damping factor.

5) Curves representing the amplitude of non-dimensional field variables are directly proportional to time parameter. Indicating that greater the value of time parameter, higher the amplitude of wave propagating through the medium. Signifying the fact that laser pulse is having increasing effect on plane wave generated in homogeneous thermoelastic medium in context of dual-phase-lag heat conduction model as in representation of [25, 26].

References

M. I. A. Othman and E. M. Abd-Elaziz, “Dual-phase-lag model on micropolar thermoelastic rotating medium under the effect of thermal load due to laser pulse,” Indian Journal of Physics, Vol. 94, No. 7, pp. 999–1008, Jul. 2020, https://doi.org/10.1007/s12648-019-01552-1

Publisher
M. I. A. Othman, W. M. Hasona, and E. M. Abd-Elaziz, “The influence of thermal loading due to laser pulse on generalized micropolar thermoelastic solid with comparison of different theories,” Multidisciplinary Modeling in Materials and Structures, Vol. 10, pp. 328–345, 2014.

Publisher
X. Wang and X. Xu, “Thermoelastic wave in metal induced by ultrafast laser pulses,” Journal of Thermal Stresses, Vol. 25, No. 5, pp. 457–473, May 2002, https://doi.org/10.1080/01495730252890186

Publisher
M. I. A. Othman, W. M. Hasona, and E. M. Abd-Elaziz, “The effect of rotation on the problem of fiber-reinforced under generalized magnetothermoelasticity subject to thermal loading due to laser pulse: a comparison of different theories,” Canadian Journal of Physics, Vol. 92, No. 9, pp. 1002–1015, Sep. 2014, https://doi.org/10.1139/cjp-2013-0321

Publisher
E. Abd-Elaziz, M. Marin, and M. Othman, “On the effect of Thomson and initial stress in a thermo-porous elastic solid under G-N electromagnetic theory,” Symmetry, Vol. 11, No. 3, p. 413, Mar. 2019, https://doi.org/10.3390/sym11030413

Publisher
N. Sarkar, S. Mondal, and M. I. A. Othman, “Effect of the laser pulse on transient waves in a non – local thermoelastic medium under Green-Naghdi theory,” Structural Engineering and Mechanics, Vol. 74, No. 4, pp. 471–479, 2020.

Search CrossRef
D. Y. Tzou, “A unified field approach for heat conduction from macro – to micro-scales,” Journal of Heat Transfer, Vol. 117, No. 1, pp. 8–16, Feb. 1995, https://doi.org/10.1115/1.2822329

Publisher
S. Chiriţă, M. Ciarletta, and C. D. ’Apice, “On the theory of thermoelasticity with microtemperatures,” Journal of Mathematical Analysis and Applications, Vol. 397, No. 1, pp. 349–361, Jan. 2013, https://doi.org/10.1016/j.jmaa.2012.07.061

Publisher
R. Quintanilla and R. Racke, “A note on stability in dual-phase-lag heat conduction,” International Journal of Heat and Mass Transfer, Vol. 49, No. 7-8, pp. 1209–1213, Apr. 2006, https://doi.org/10.1016/j.ijheatmasstransfer.2005.10.016

Publisher
R. Prasad, R. Kumar, and S. Mukhopadhyay, “Propagation of harmonic plane waves under thermoelasticity with dual-phase-lags,” International Journal of Engineering Science, Vol. 48, No. 12, pp. 2028–2043, Dec. 2010, https://doi.org/10.1016/j.ijengsci.2010.04.011

Publisher
M. I. A. Othman and E. M. Abd-Elaziz, “The effect of thermal loading due to laser pulse in generalized thermoelastic medium with voids in dual phase lag model,” Journal of Thermal Stresses, Vol. 38, No. 9, pp. 1068–1082, Sep. 2015, https://doi.org/10.1080/01495739.2015.1073492

Publisher
B. Singh, “Wave propagation in dual-phase-lag anisotropic thermoelasticity,” Continuum Mechanics and Thermodynamics, Vol. 25, No. 5, pp. 675–683, Sep. 2013, https://doi.org/10.1007/s00161-012-0261-x

Publisher
H. M. Youssef and A. A. El-Bary, “Two-temperature generalized thermo-elastic medium thermally excited by time exponentially decaying laser pulse,” International Journal of Structural Stability and Dynamics, Vol. 16, No. 3, p. 1450102, Apr. 2016, https://doi.org/10.1142/s0219455414501028

Publisher
P. Říha, “On the microcontinuum model of heat conduction in materials with inner structure,” International Journal of Engineering Science, Vol. 14, No. 6, pp. 529–535, Jan. 1976, https://doi.org/10.1016/0020-7225(76)90017-3

Publisher
M. I. A. Othman and E. M. Abd-Elaziz, “Effect of initial stress and Hall current on a magneto-thermoelastic porous medium with microtemperatures,” Indian Journal of Physics, Vol. 93, No. 4, pp. 475–485, Apr. 2019, https://doi.org/10.1007/s12648-018-1313-2

Publisher
D. Iasan, “On a theory of micromorphic elastic solids with microtemperatures,” Journal of Thermal Stresses, Vol. 24, No. 8, pp. 737–752, Aug. 2001, https://doi.org/10.1080/014957301300324882

Publisher
H. W. Lord and Y. Shulman, “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, pp. 299–309, Sep. 1967, https://doi.org/10.1016/0022-5096(67)90024-5

Publisher
Arvind Kumar, Rajneesh Kumar, and S. M. Abo-Dahab, “Mathematical model for Rayleigh waves in microstretch thermoelastic medium with microtemperatures,” Journal of Applied Science and Engineering, Vol. 20, No. 2, pp. 149–156, Jun. 2017, https://doi.org/10.6180/jase.2017.20.2.02

Publisher
M. I. A. Othman, R. S. Tantawi, and E. M. Abd-Elaziz, “Effect of initial stress on a porous thermo-elastic medium with microtemperatures,” Journal of Porous Media, Vol. 19, No. 2, pp. 155–172, 2016.

Publisher
M. I. A. Othman and E. M. Abd-Elaziz, “Plane waves in a magneto-thermoelastic solids with voids and microtemperatures due to hall current and rotation,” Results in Physics, Vol. 7, pp. 4253–4263, 2017, https://doi.org/10.1016/j.rinp.2017.10.053

Publisher
M. A. Ezzat, “The relaxation effects of the volume properties of electrically conducting viscoelastic material,” Materials Science and Engineering: B, Vol. 130, No. 1-3, pp. 11–23, Jun. 2006, https://doi.org/10.1016/j.mseb.2006.01.020

Publisher
E. M. Abd‐Elaziz and M. I. A. Othman, “Effect of Thomson and thermal loading due to laser pulse in a magneto‐thermo‐elastic porous medium with energy dissipation,” ZAMM – Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 99, No. 8, Aug. 2019, https://doi.org/10.1002/zamm.201900079

Publisher
M. I. Othman and A. E. E. Abouelregal, “The effect of pulsed laser radiation on a thermoviscoelastic semi-infinite solid under two-temperature theory,” Archives of Thermodynamics, Vol. 38, No. 3, pp. 77–99, Sep. 2017, https://doi.org/10.1515/aoter-2017-0017

Publisher
M. I. A. Othman and R. S. Tantawi, “The effect of a laser pulse and gravity field on a thermoelastic medium under Green–Naghdi theory,” Acta Mechanica, Vol. 227, No. 12, pp. 3571–3583, Dec. 2016, https://doi.org/10.1007/s00707-016-1683-5

Publisher
H. Steeb, J. Singh, and S. K. Tomar, “Time harmonic waves in thermoelastic material with microtemperatures,” Mechanics Research Communications, Vol. 48, pp. 8–18, Mar. 2013, https://doi.org/10.1016/j.mechrescom.2012.11.006

Publisher
S. Deswal, S. S. Sheoran, and K. K. Kalkal, “A two-dimensional problem in magnetothermoelasticity with laser pulse under different boundary conditions,” Journal of Mechanics of Materials and Structures, Vol. 8, No. 8-10, pp. 441–459, Dec. 2013, https://doi.org/10.2140/jomms.2013.8.441

Publisher

Cited by

Modal Analysis and Structural Optimization of MEMS Acoustic Emission Sensing Micro-elements with Variable Area for Improved Anti-interference Capability

Ning Su

(2024)

About this article

Received

02 August 2021

Accepted

02 October 2021

Published

11 November 2021

DOI

https://doi.org/10.21595/jets.2021.22166

Keywords

thermoelastic wave

thermal loading

micro-temperature

DPL model

harmonic solution

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 23

Plane waves in an isotropic thermoelastic diffusive material using strain gradient theory

Baljeet Singh, Himanshu Singla

Research article

2023 05 01

Wave propagation in different theories of fractional thermoelasticity

Baljeet Singh

Research article

2022 10 25

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Hamdy M. Youssef, Raafat A. A. Salem

Research article

2022 06 30

Dual-phase-lag model on microelongated thermoelastic rotating medium

Mohamed I. A. Othman, Sarhan Y. Atwa, E. E. M. Eraki, Mohamed F. Ismail

A. Jahangir, A. Dar, and M. I. A. Othman, “Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model,” Journal of Engineering and Thermal Sciences, Vol. 1, No. 2, pp. 54–64, Nov. 2021, https://doi.org/10.21595/jets.2021.22166

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2021.22166
UR  - https://doi.org/10.21595/jets.2021.22166
TI  - Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model
T2  - Journal of Engineering and Thermal Sciences
AU  - Jahangir, Adnan
AU  - Dar, Adiya
AU  - Othman, Mohamed I. A.
PY  - 2021
DA  - 2021/11/11
PB  - JVE International Ltd.
SP  - 54-64
IS  - 2
VL  - 1
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Jahangir_2021,
	doi = {10.21595/jets.2021.22166},
	url = {https://doi.org/10.21595/jets.2021.22166},
	year = 2021,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {1},
	number = {2},
	pages = {54--64},
	author = {Adnan Jahangir and Adiya Dar and Mohamed I. A. Othman},
	title = {Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the {DPL} model},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]A. Jahangir, A. Dar, and M. I. A. Othman, “Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model,” Journal of Engineering and Thermal Sciences, vol. 1, no. 2, pp. 54–64, Nov. 2021, doi: 10.21595/jets.2021.22166.

Copy IEEE

Copied to clipboard!

Jahangir, Adnan, Adiya Dar, and Mohamed I. A. Othman. “Influence of Laser Pulse on Plane Waves Propagating in a Thermoelastic Medium with Micro-Temperature under the DPL Model.” Journal of Engineering and Thermal Sciences 1, no. 2 (November 11, 2021): 54–64. https://doi.org/10.21595/jets.2021.22166.

Copy Chicago

Copied to clipboard!

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Abstract

1. Introduction

2. Problem formulation and basic equations

2.1. Harmonic solution of the problem

2.2. Boundary conditions

2.3. Numerical results and discussion

3. Conclusions

References

Cited by

About this article

Related Articles