Abstract
The large engineering building structures are costly and thus complex to maintain due to their chances of failure under various hazardous conditions. These buildings are needed to be protected against the damage due to the hazards like earthquake, wind, seismic waves, etc. This article focuses on the investigation of vibration mechanism and control strategies for protection of buildings from the hazardous situations. The article presents a robust solution of utilization of magnetorheological dampers for vibration control applications in complex structures. It aims at developing a reliable decentralized model to track and monitor the building structures and control them before the earthquake actions are encountered. This article develops a novel dynamically optimized and decentralized mechanism using the PID controller for the self-regulation of conventional PID controller-based method. The major goal of decentralization is to ensure that each of the subsystem is compatible with one another and can also work independently with a higher efficiency at the time of fault. The combination of decentralization and self-regulation is tested for a tall building structural model with 10 floors. The proposed approach is compared with the conventional PID based mechanism under the faulty condition in order to illustrate its dynamism and usefulness for practical implementation. The proposed simulated model provides 95.54 % earthquake tracking precision and can be used for developing the earthquake protective schemes for the adequate survivability of tall building structures as well as to safeguard the human occupant in it.
Highlights
- It aims at developing a reliable earthquake protection system for safeguarding the survivability of tall building structures.
- A novel dynamically decentralized approach is developed in this work using the PID controller for the self-regulation of conventional PID controller-based mechanisms.
- The major goal is to ensure that each of the subsystem is compatible with one another and can also work independently with a higher efficiency.
- The ant colony optimization (ACO) methodology has been used for self-regulatory optimization of the differential as well as integral values before processing them through the PID controller.
- The advantages of decentralization as well as self-regulation is combined in the proposed methodology and numerical simulation of a tall building structural model with 10 floors is done.
- The proposed approach is also compared with the conventional PID based mechanism is illustrate its dynamism and usefulness for practical implementation.
1. Introduction
The manufacturing technology has made several advancements by emerging the usage of new construction materials which have higher strength, better performance and is light weight at the same time. When this construction mechanism is integrated with the high-quality controlling mechanisms during the manufacturing and construction process, lead to the complex structures which are computationally efficient [1, 2]. The rise in structure complexity has increased the construction cost as well as the requirement of safety for these structures during the hazardous conditions like earthquake, wind induction, etc. the protection of such tall building structures as well as the occupants is necessary area of research nowadays [3]. The random occurrence of earthquakes can propagate the ground motion that may arise the seismic waves bringing the vibration mechanism on the earth. The major drawbacks of unpredictable earthquakes, winds and other natural hazardous condition can occasionally be seen on the buildings which threatens the human lives. Thus, it is required to engage effectual vibration control mechanisms for protection of building structures against such calamities [4, 5]. Various types of vibration control mechanisms for earthquake protection are depicted in Fig. 1.
Fig. 1Different types of vibration control mechanisms for earthquake protection
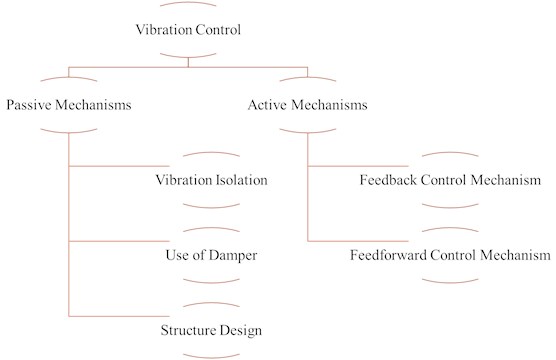
Significant research work is going on in this field for protecting the tall building infrastructures from various natural load conditions like wind and earthquake. However, it should be noted that the building structures cannot be designed such that they withstand all the possible external load conditions and provide damage control [6, 7]. It is notices that the damping characteristics of the building structures plays a vital role in rising the distress during the unpredictable environmental load condition resulting in unacceptable failure. Various structure control technologies have been incorporated for such controlling mechanisms in the past few decades [8]. The major controlling strategies adopted for structural vibration control are active control by providing the counter forces, passive control by involving energy dissipation and other semi-active controlling mechanisms [9, 10]. The passive control mechanisms do not require any external energy and therefore, are commonly used. But the drawback is that they cannot be adjusted and tuned for external loading conditions. The active control systems however, require the external energy supply and are thus used in active mass driver, mass damper, etc. however they also possess a drawback of power failure under the extreme load conditions. The semi active control is however applicable for practical implementation due to their inherent reliability and versatile nature. The recent research work going in this field use to combine the hybrid mechanism for structural protection and control. The hybrid control systems improve the performance of both active as well as passive system by reducing the energy requirements as well as creating a fail-safe system.
This article aims at developing a reliable earthquake protection system for safeguarding the survivability of tall building structures. Various efforts have been made by the researchers in providing a centralized control strategy ensuring least displacement of the building structures during the earthquake. A novel dynamically decentralized approach is developed in this work using the PID controller for the self-regulation of conventional PID controller-based mechanisms. The major goal is to ensure that each of the subsystem is compatible with one another and can also work independently with a higher efficiency. The ant colony optimization (ACO) methodology has been used for self-regulatory optimization of the differential as well as integral values before processing them through the PID controller. The advantages of decentralization as well as self-regulation is combined in the proposed methodology and numerical simulation of a tall building structural model with 10 floors is done. Additionally, the proposed approach is also compared with the conventional PID based mechanism is illustrate its dynamism and usefulness for practical implementation. The proposed methodology outperforms the other controlling mechanisms in its dynamic decentralized mode yielding in superior and reliable outcomes.
The rest of this paper is organized as follows. Section 2 provides the basic methodologies being utilized for vibration analysis of the building structures. Section 3 presents the development of a new method for controlling the undesirable vibrations causes in the tall building structures. The simulation outcomes are illustrated in Section 4 and the effectiveness of the proposed methodology is justified. Finally, the major conclusions drawn from the study are portrayed in Section 5.
2. Literature review
The past few decades have motivated the researchers in including a variety of techniques for vibration control and to save the large structural buildings from severe damage. The methods may include the linear quadratic regulation [11], neural networks [12], application of fuzzy methodology [13], proportional integral derivative (PID) based disturbance rejection [14] and many other algorithms [15]. The authors in [16] proposed a two-look sliding system that can dynamically predict the state of the controlling device in the high-rise buildings. The neural network-based vibration reduction mechanism was proposed by [17] for protecting the large building structured from earthquakes and the real earthquake testing of this method is done at Tohoku 2011 and Boumerdès 2003 earthquakes. A controller model was proposed by the authors in [18] by combining the tan hyperbolic function and the sliding mode terminal in order to obtain stabilized outcomes while avoiding chattering. The PID controllers have widely being used in the practical practices of earthquake vibration monitoring due to simplicity in structure and ease of implementation. However, researchers observed that the dynamic requirements vibration analysis cannot be dealt using the conventional PID approaches. For such application, neither PD or PID controllers provides satisfactory outcomes. In order to improve the performance of these controllers, some of the authors presented the fractional order based PID controllers [19]. This methodology was used for motor controlling mechanism [20], for the control of mechanical magnetic bearings [21], robotic control [22], control of tall building structures [23] and several other applications [24-26]. However, there are several shortcomings of these methods which are needed to be further improved for dealing with the complex systems.
There have been several advancements in using the hybrid control practices for the vibration analysis as they have the advantages of both active and passive controlling mechanisms. The major advantage lies in its compactness, efficiency and practical ability to work under real controlling conditions. But the drawback with these methods is the need of external power source for active control purposes. The recent development in the utilization of dampers for controlling strategies has also grabbed the attention of the researchers. The majority of dampers are used for friction analysis, analysis of stiffness, extrusion detection and other purposes. High-capacity oil dampers have also been introduced along with friction dampers, hysteric dampers, semi-active oil dampers and many more [27]. The authors in [28] introduced a novel strategy by re-setting the semi-active stiffness of the dampers being utilized for the base isolation of non-linear buildings in order to provide the information of near field earthquake conditions. Big data analytics have also been frequently used in the complex heterogeneous environment for getting insight of the data. Authors in [29] provided a review of utilization of big data in the construction sector for data processing, storage and data distribution. Various methodologies involve data mining, statistics, clustering, regression, classification and natural language processing for big data evaluation [29, 30]. In the recent years, the new strategies have been adopted for overcoming the big data complexities like probabilistic graphics, support vector machines, and various other regression, clustering and data mining methods [31-33].
From the existing literature review, it is observed that for the big data based tall structural analysis, there is a need to propose novel mechanisms to reduce the complexity of data processing/analysis and reduce time consumption complexities as well. An effective approach is required in the construction sector for the controlling mechanism of tall buildings from natural calamities like earthquake, winds, etc.
3. Material and Methods
In this article initially the horizontal vibration mechanism of the 10-floor tall building structure is analysed and an actively dynamic strategy is adopted for the analysis of conventional control strategy. The MATLAB/Simulink platform was utilized for simulation and investigation of the tall building structures. There are various earthquake mitigation aspects considered for designing the proposed model which are detailed as follows:
1) Stiffness and strength of building: While designing a control mechanism for earthquake resistant, the safety aspect of lateral stiffness and strength is taken into account. This is a very important aspect which should be kept in mind while building a control mechanism as building shifts left or right vertically during the occurrence of earthquake.
2) Regularity: The regularity aspect is also considered as it refers to the building movement when earthquake occurs. If during an earthquake the building become irregular, it will lead to weakness and may lead to concentrated damage to the entire structure.
3) Redundancy: Redundancy ensures that there can be multiple earthquake control strategies that fails which may add on to the building cost. Thus, it is advised by the earthquake professional to learn from redundancies and built an effective earthquake control mechanism.
4) Foundation: The major important building characteristic for tall building structure is its foundation which should be resistant of natural risk disasters. This characteristic is necessary for the long term survival of building structures and leads to the stability of a building design.
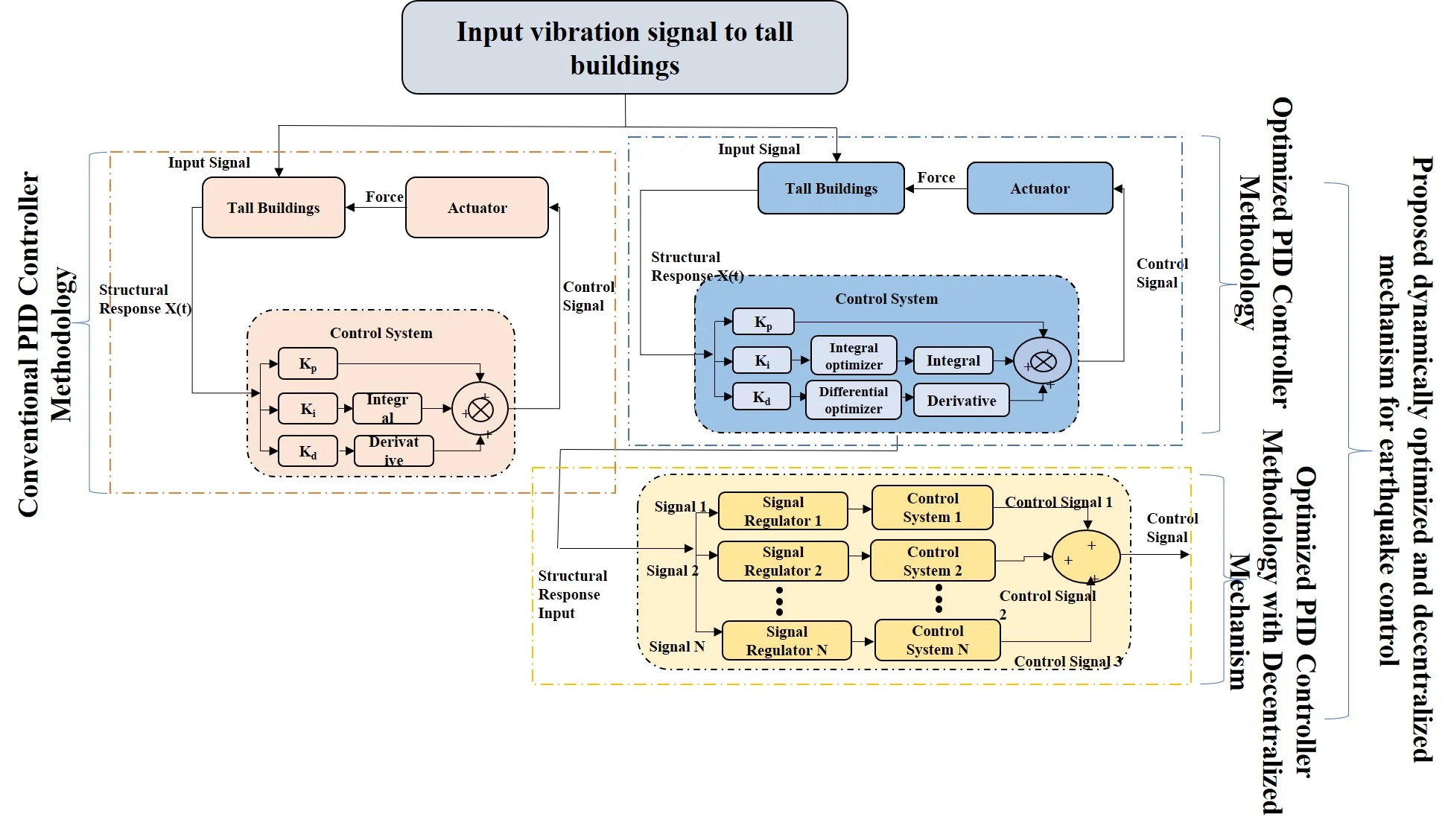
All of these measures are considered building the dynamic optimization strategy for earthquake control and the input vibration signal from buildings is considered as an input for the proposed design scheme. The methodology for the design scheme of proposed dynamically optimized and decentralized mechanism for earthquake control is shown in Fig. 2.
Fig. 2Design scheme of the proposed control mechanism
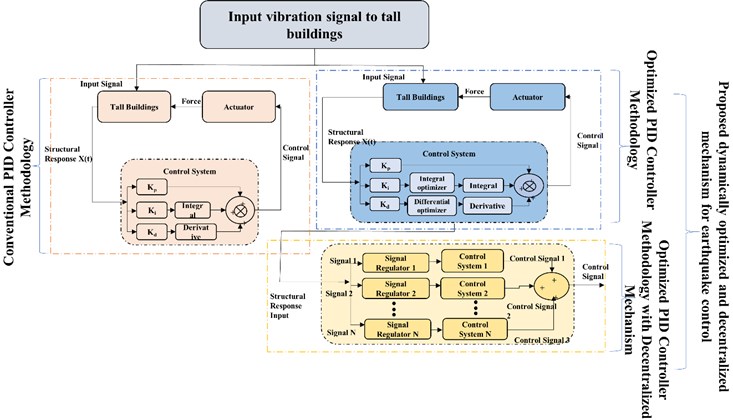
The design scheme of the proposed control mechanism consists of an input vibration signal which is provided to the conventional PID controller and the proposed optimization-based model. A decentralization aspect is also introduced in the proposed PID control-based method which provides a self-regulatory mechanism and optimal parameters for earthquake control. The proposed dynamically optimized and decentralized mechanism for earthquake provides an efficient combination of decentralization and self-regulation for the faulty condition as well, illustrating its dynamism and usefulness for practical implementation. The submodules for the design scheme are detailed in the following subsections.
3.1. Conventional PID controller methodology
The conventional PID control system for tall building structure is schematized in Fig. 3.
Fig. 3Schematics of conventional PID control system for tall building structure
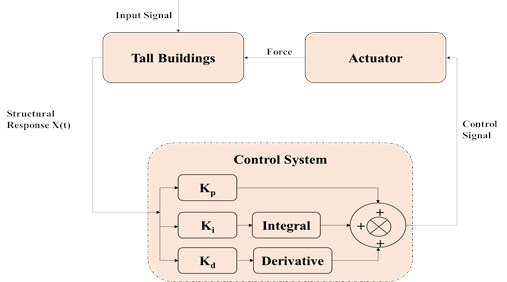
The acceleration produces by the seismic waves is considered as the input for the simulation and the actuator output force is further processed and controlled as per the corresponding displacement signal. The combined structural response of the seismic wave acceleration and actuator is further processed through the PID control system. For structural vibration control, the dynamic model is denoted by Eq. (1):
where, denoting the unit vector, structural mass, seismic wave acceleration. and denotes damping and stiffness matrix parameters, denotes the actuator location matrix, signifies the actuator control vector, represents the external excitation vector. are the acceleration, velocity and the displacement vectors. This dynamic model is transformed into the state space as indicated in Eq. (2):
where the represents , here represents the seismic wave acceleration, p is the column position vector for acting of force which is generated by actuator.
3.2. Optimized PID controller methodology
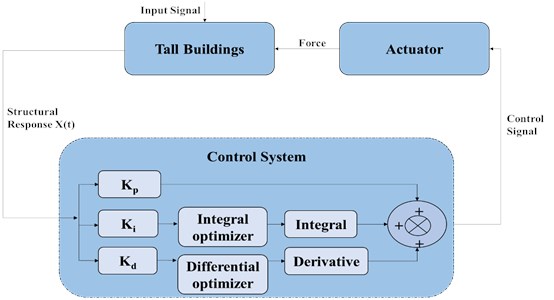
An optimized PID controller mechanism for earthquake control is proposed in this article which utilizes the ACO optimization module for integral and differential optimizer before processing it through the PID control system. This modification makes it self-regulatory and helps in optimizing and controlling the parameters as compared to the conventional PID controller method. The schematic of proposed earthquake control model for tall building structures is presented in Fig. 4.
The proposed earthquake control model for tall building structures provides improved performance by utilization of an integral and a differential order optimizer which allow the time varying optimization comparative to the fixed control in case of conventional PID controller. The proposed control system utilizes a controlling unit, an actuator unit and an optimization unit to continuously detect the occurrence of an earthquake load event. However, it was noted, that this system may not provide exact controlling mechanism in case of sudden earthquake events, thus the safety issue emerges.
Fig. 4Schematic of proposed earthquake control model for tall building structures
3.3. Optimized PID controller methodology with decentralized mechanism
Further the proposed approach is modified by integrating it with a decentralized mechanism. The decentralization is employed in order to increase the system reliability by separating the control system into different sub-systems. Each of these subsystems comprises of several regulators and various control systems. The decentralized approach of the proposed system is depicted in Fig. 5.
Fig. 5Decentralized approach of the proposed system
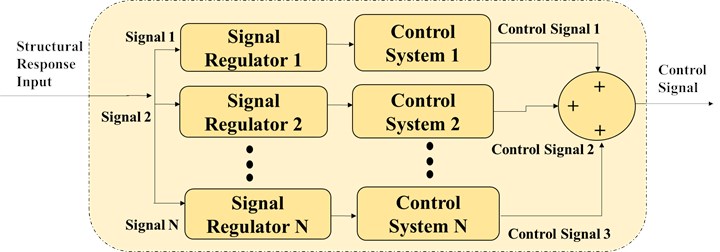
In the decentralization case, when any of the controller subsystem fails, the remaining takes the load and guarantees the controlling mechanisms and therefore provide some of the relevant control action, without completely shutting down the system in case of centralized controlling approach. The signal amplitude is regulated using a separate regulator module in which ACO optimization is accomplished. Further, the optimized signal is carried to the corresponding control systems. In case of fault detection in any one of the decentralized sub-system, the self-regulation strategy works out and the optimal parameters are updated for the control system. The proposed self-regulatory control mechanism for earthquake occurrence situation involves a quality check for all the controlling sub-system. If the fault in any of the subsystem occurs, the control system parameters are immediately updated as per the fault situation. Further, the control system generates the corresponding regulatory action plan. This methodology provides reliable and optimal outcomes for structural vibrations occurring due to earthquake excitation.
4. Results and discussion
The outcomes of the proposed approach are analysed for 10-floor tall building under the convention PID mechanism, the proposed optimized control system and the optimized control system with decentralization. The outcomes are obtained for the acceleration earthquake signal tracking and control. The reliability of the system is also checked under the faulty decentralized condition when the one of the sub-systems in the complete set fails and other take the charge of optimization.
4.1. Outcomes of proposed optimized PID controller methodology
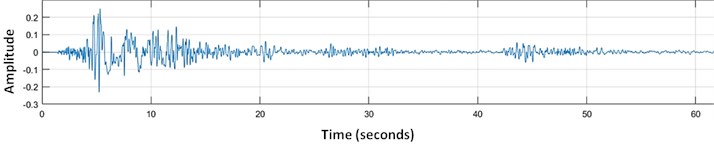
The vibration analysis of a 10-floor tall building is done using the acceleration signal during the occurrence of earthquake. The slightest of the accelerations are noticed by the control system. The vibration signal acceleration amplitude vs time graph is shown in Fig. 6.
Fig. 6Accelerated vibration signal during earthquake
The conventional PID control was tested initially for the checking the reference tracking mechanism of earthquake monitoring and control system and the outcomes when compared with the ideal control are depicted in Fig. 7.
From the outcomes obtained for the conventional methodology it can be seen that there is a lot of gap between the ideal control mechanism and the convention PID one. Due to this limitation, an optimization approach is proposed in this work which initially optimizes the deferential and integral values before passing it to the control system. From the outcomes obtained for this modification, it can be seen that a lot of improvement is witnessed for the control mechanism tracking and the comparison can be realized from Fig. 8.
The ACO optimization approach when integrated at the initial stage, before passing the signal through the control system much better outcomes are obtained than the conventional PID controller. Fig. 8 provides the reference tracking comparison of the ideal control with the proposed PID methodology with ACO optimization.
Fig. 7Outcomes obtained for conventional PID controller
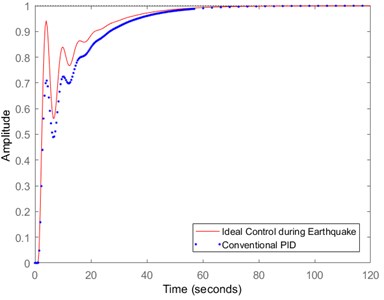
Fig. 8Comparison of ideal control with proposed optimized (ACO) PID controller methodology
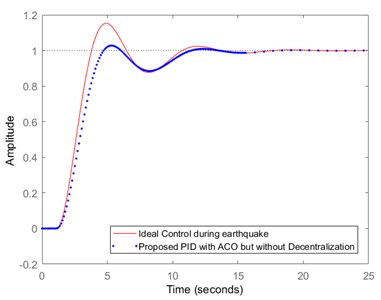
The proposed ACO optimization system may not provide exact controlling mechanism in case of sudden earthquake events and the safety issue emerges. Thus, for further improvement in the system reliability and to counter the sudden earthquake events, decentralization mechanism is added in the proposed optimized (ACO) PID Controller Methodology.
4.2. Outcomes of the proposed PID method with ACO optimization and decentralized mechanism
The decentralization feature when combined with the ACO optimization utilizes a series of sub-system so that when any of the controller subsystem fails, the remaining takes the load and guarantees the controlling mechanism. Thus, this leads to an advantage of providing the relevant control action, without completely shutting down the system. The comparison of the outcomes obtained for ideal control and the proposed optimized PID controller with decentralized mechanism is depicted in Fig. 9.
In the decentralization mechanism, a series of subsystem are used which consists of separate regulator module with ACO optimizer and separate control system for each of the sub-system. Experimentation also reveals that the proposed approach provides 99.27 % tracking precision comparative to the ideal control during the earthquake.
Fig. 9Comparison of ideal control with proposed optimized PID controller and decentralized mechanism
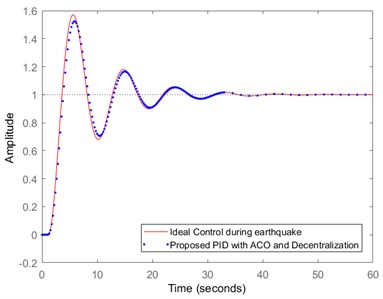
Fig. 10Comparison of ideal control with proposed optimized PID controller and decentralized mechanism during fault condition
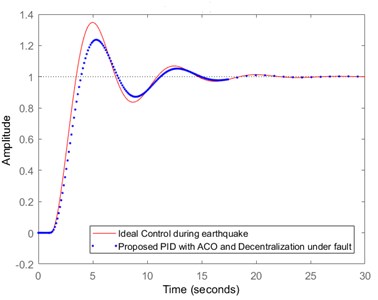
4.3. Outcomes of the proposed optimization and decentralized mechanism under faulty condition
The earthquake tracking precision is also evaluated for the fault condition when any of the sub-system in the decentralized control mechanism is at fault. In this case, the self-regulation strategy of the system is triggered and the optimal parameters are immediately updated for the control system while excluding the faulty sub-system. The control mechanism in this case is not as accurate as that of the complete decentralized methodology but the corresponding parameters are nearly optimized and the regulatory action plan is initiated. The outcomes obtained for the proposed optimization and decentralized mechanism under faulty condition is compared with the ideal control case and it is depicted in Fig. 10.
The outcomes obtained reveals that during the faulty condition, the proposed methodology provides 95.54 % of tracking precision comparative to the ideal control during the earthquake. The optimized methodology provides reliable and dynamic results for the tall structural vibrations which occurs due to the earthquake excitation.
5. Conclusions
In this article, a reliable earthquake protection system is developed using ACO optimization and decentralization mechanism in order to provide the protective scheme for tall building survivability as well as to safeguard the occupants. A dynamically decentralized approach is proposed in this work using the PID controller for the self-regulation during the faulty condition in case, any of the sub-system goes down. This work aims at ensuring that each of the subsystem is compatible with one another and can also work independently and higher tracking precision during the faulty conditions as well. The combination of optimization, decentralization and self-regulation provides better outcomes for the numerical simulation of tracking and control mechanism during the earthquake scenario. The tracking precision of 99.27 % is witnessed for no fault decentralized mechanism and during the faulty condition the proposed simulated model provides 95.54 % earthquake tracking precision. The proposed optimization methodology outperforms the other controlling mechanisms in its dynamic decentralized mode providing superior and reliable outcomes establishing its usefulness for practical implementation.
References
-
B. Kavyashree, S. Patil, and V. S. Rao, “Review on vibration control in tall buildings: from the perspective of devices and applications,” International Journal of Dynamics and Control, Vol. 9, No. 3, pp. 1316–1331, Sep. 2021, https://doi.org/10.1007/s40435-020-00728-6
-
Z. Rahimi, W. Sumelka, S. R. Ahmadi, and D. Baleanu, “Study and control of thermoelastic damping of in-plane vibration of the functionally graded nano-plate,” Journal of Vibration and Control, Vol. 25, No. 23-24, pp. 2850–2862, Dec. 2019, https://doi.org/10.1177/1077546319861009
-
H. Sun, M. Fan, and A. Sharma, “Design and implementation of construction prediction and management platform based on building information modelling and three‐dimensional simulation technology in industry 4.0,” IET Collaborative Intelligent Manufacturing, Mar. 2021, https://doi.org/10.1049/cim2.12019
-
W. Cai, B. Yu, F. Wu, and J. Shao, “Seismic response and vibration reduction analysis of suspended structure under wave passage excitation,” Advances in Civil Engineering, Vol. 2020, pp. 1–13, Jul. 2020, https://doi.org/10.1155/2020/6468181
-
X. Ren et al., “Design of multi-information fusion based intelligent electrical fire detection system for green buildings,” Sustainability, Vol. 13, No. 6, p. 3405, Mar. 2021, https://doi.org/10.3390/su13063405
-
R. Chen and A. Sharma, “Construction of complex environmental art design system based on 3D virtual simulation technology,” International Journal of System Assurance Engineering and Management, Apr. 2021, https://doi.org/10.1007/s13198-021-01104-z
-
K. Xu, L. Chen, M. Wang, A. M. Lopes, J. A. Tenreiro Machado, and H. Zhai, “Improved decentralized fractional PD control of structure vibrations,” Mathematics, Vol. 8, No. 3, p. 326, Mar. 2020, https://doi.org/10.3390/math8030326
-
G. Dhiman et al., “MOSOA: A new multi-objective seagull optimization algorithm,” Expert Systems with Applications, Vol. 167, p. 114150, Apr. 2021, https://doi.org/10.1016/j.eswa.2020.114150
-
A. Jajarmi, M. Hajipour, S. S. Sajjadi, and D. Baleanu, “A robust and accurate disturbance damping control design for nonlinear dynamical systems,” Optimal Control Applications and Methods, Vol. 40, No. 3, pp. 375–393, May 2019, https://doi.org/10.1002/oca.2480
-
M. Fan and A. Sharma, “Design and implementation of construction cost prediction model based on SVM and LSSVM in industries 4.0,” International Journal of Intelligent Computing and Cybernetics, Vol. 14, No. 2, pp. 145–157, Apr. 2021, https://doi.org/10.1108/ijicc-10-2020-0142
-
Q. Sun, X. Wang, and Y.-H. Chen, “Adaptive robust control for dual avoidance-arrival performance for uncertain mechanical systems,” Nonlinear Dynamics, Vol. 94, No. 2, pp. 759–774, Oct. 2018, https://doi.org/10.1007/s11071-018-4392-x
-
J. Wang et al., “Neural terminal sliding-mode control for uncertain systems with building structure vibration,” Complexity, Vol. 2019, pp. 1–9, Apr. 2019, https://doi.org/10.1155/2019/1507051
-
R. Guclu and H. Yazici, “Vibration control of a structure with ATMD against earthquake using fuzzy logic controllers,” Journal of Sound and Vibration, Vol. 318, No. 1-2, pp. 36–49, Nov. 2008, https://doi.org/10.1016/j.jsv.2008.03.058
-
S. Thenozhi and W. Yu, “Stability analysis of active vibration control of building structures using PD/PID control,” Engineering Structures, Vol. 81, pp. 208–218, Dec. 2014, https://doi.org/10.1016/j.engstruct.2014.09.042
-
X.-Y. Zhang, S.-Q. Zhang, Z.-X. Wang, X.-S. Qin, R.-X. Wang, and R. Schmidt, “Disturbance rejection control with H∞ optimized observer for vibration suppression of piezoelectric smart structures,” Mechanics and Industry, Vol. 20, No. 2, p. 202, 2019, https://doi.org/10.1051/meca/2019015
-
M. Soleymani, A. H. Abolmasoumi, H. Bahrami, A. Khalatbari-S., E. Khoshbin, and S. Sayahi, “Modified sliding mode control of a seismic active mass damper system considering model uncertainties and input time delay,” Journal of Vibration and Control, Vol. 24, No. 6, pp. 1051–1064, Mar. 2018, https://doi.org/10.1177/1077546316657477
-
K. Zizouni, L. Fali, Y. Sadek, and I. K. Bousserhane, “Neural network control for earthquake structural vibration reduction using MRD,” Frontiers of Structural and Civil Engineering, Vol. 13, No. 5, pp. 1171–1182, Oct. 2019, https://doi.org/10.1007/s11709-019-0544-4
-
J. Maruani, I. Bruant, F. Pablo, and L. Gallimard, “Active vibration control of a smart functionally graded piezoelectric material plate using an adaptive fuzzy controller strategy,” Journal of Intelligent Material Systems and Structures, Vol. 30, No. 14, pp. 2065–2078, Aug. 2019, https://doi.org/10.1177/1045389x19853628
-
S. Etedali, A.-A. Zamani, and S. Tavakoli, “A GBMO-based PI λ D μ controller for vibration mitigation of seismic-excited structures,” Automation in Construction, Vol. 87, pp. 1–12, Mar. 2018, https://doi.org/10.1016/j.autcon.2017.12.005
-
A. Coronel-Escamilla, F. Torres, J. F. Gómez-Aguilar, R. F. Escobar-Jiménez, and G. V. Guerrero-Ramírez, “On the trajectory tracking control for an SCARA robot manipulator in a fractional model driven by induction motors with PSO tuning,” Multibody System Dynamics, Vol. 43, No. 3, pp. 257–277, Jul. 2018, https://doi.org/10.1007/s11044-017-9586-3
-
J. Zhong and L. Li, “Fractional-order system identification and proportional-derivative control of a solid-core magnetic bearing,” ISA Transactions, Vol. 53, No. 4, pp. 1232–1242, Jul. 2014, https://doi.org/10.1016/j.isatra.2014.05.008
-
M. F. Silva, J. A. T. Machado, and A. M. Lopes, “Fractional order control of a hexapod robot,” Nonlinear Dynamics, Vol. 38, No. 1-4, pp. 417–433, Dec. 2004, https://doi.org/10.1007/s11071-004-3770-8
-
A.-A. Zamani, S. Tavakoli, and S. Etedali, “Fractional order PID control design for semi-active control of smart base-isolated structures: A multi-objective cuckoo search approach,” ISA Transactions, Vol. 67, pp. 222–232, Mar. 2017, https://doi.org/10.1016/j.isatra.2017.01.012
-
G. Baruah, S. Majhi, and C. Mahanta, “Auto-tuning of fractional order PID controller for a class of processes and experimental validation using a coupled tank system,” Journal of Control and Systems Engineering, Vol. 4, No. 1, pp. 121–140, Dec. 2016, https://doi.org/10.18005/jcse0401012
-
J. Yang and X. Hou, “Robust stability analysis of fractional-order linear systems with polytopic uncertainties,” in the 3rd International Conference, Vol. 257, pp. 274–284, 2018, https://doi.org/10.1145/3265639.3265646
-
L. Chen, J. Cao, R. Wu, J. A. Tenreiro Machado, A. M. Lopes, and H. Yang, “Stability and synchronization of fractional-order memristive neural networks with multiple delays,” Neural Networks, Vol. 94, pp. 76–85, Oct. 2017, https://doi.org/10.1016/j.neunet.2017.06.012
-
Y. Ikeda, M. Yamamoto, T. Furuhashi, and H. Kurino, “Recent research and development of structural control in Japan,” Japan Architectural Review, Vol. 2, No. 3, pp. 219–225, Jul. 2019, https://doi.org/10.1002/2475-8876.12081
-
K. K. Walsh, G. Sallar, and E. P. Steinberg, “Hybrid base-isolation of a nonlinear building using a passive resettable stiffness damper,” Engineering Structures, Vol. 178, pp. 206–211, Jan. 2019, https://doi.org/10.1016/j.engstruct.2018.10.037
-
S. K. Vavilala, V. Thirumavalavan, R. Thota, and S. Natarajan, “Design of the fractional order internal model controller using the swarm intelligence techniques for the coupled tank system,” Turkish Journal of Electrical Engineering and Computer Sciences, Vol. 29, No. 2, pp. 1207–1225, 2021, https://doi.org/10.3906/elk-2005-17
-
A. Entezami, H. Sarmadi, B. Behkamal, and S. Mariani, “Big data analytics and structural health monitoring: A statistical pattern recognition-based approach,” Sensors, Vol. 20, No. 8, p. 2328, Apr. 2020, https://doi.org/10.3390/s20082328
-
C. Cremona and J. Santos, “Structural health monitoring as a big-data problem,” Structural Engineering International, Vol. 28, No. 3, pp. 243–254, Jul. 2018, https://doi.org/10.1080/10168664.2018.1461536
-
A. Javidialesaadi and N. E. Wierschem, “Energy transfer and passive control of single-degree-of-freedom structures using a one-directional rotational inertia viscous damper,” Engineering Structures, Vol. 196, p. 109339, Oct. 2019, https://doi.org/10.1016/j.engstruct.2019.109339
-
A. Jegatheesh and C. Agees Kumar, “Novel fuzzy fractional order PID controller for non linear interacting coupled spherical tank system for level process,” Microprocessors and Microsystems, Vol. 72, p. 102948, Feb. 2020, https://doi.org/10.1016/j.micpro.2019.102948
