Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition

Chen, Yongqi; Chen, Yang; Dai, Qinge

doi:10.21595/jve.2021.21896

Journal of Vibroengineering

Browse Journal

Submit article

Published: 11 August 2021

Check for updates

Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition

Yongqi Chen¹

Yang Chen²

Qinge Dai³

^{1, 2, 3}College of Science and Technology, Ningbo University, Ningbo, 315211, P. R. China

Corresponding Author:

Yang Chen

Cite the article Download PDF

Downloads 661

WoS Core Citations 6

CrossRef Citations 5

Abstract

The traditional multiscale entropy algorithm shows inconsistency because some points are ignored when the signal is coarsened. To solve this problem, this paper proposes an improved multiscale permutation entropy (IMSPE). Firstly, the fault signal is decomposed into several product functions (PF) by local mean decomposition (LMD). Secondly, IMSPE is proposed to extract fault features of product functions. IMSPE integrates the information of multiple coarse sequences and solves problems of entropy inconsistency. Finally, the proposed method based on LMD and IMSPE is applied into gear fault diagnosis system. The experiment shows the proposed method can distinguish different gear fault types with a higher accuracy than traditional methods.

Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition

Highlights

IMSPE is proposed to extract gear fault features.
IMSPE integrates the information of multiple coarse sequences and solves problems of entropy inconsistency.
IMSPE, LMD and LSSVM are applied into gear fault diagnosis system can distinguish different gear fault types with a higher accuracy than traditional methods.

1. Introduction

Gear box is an important mechanical part which is used to transfer power and movement. However, due to the poor working environment, gearbox is prone to various compound faults. Therefore, it is necessary to propose a fault diagnosis method for gearbox faults. For these years, vibration signal detection and diagnosis method is the most widely used gear fault detection method [1]. Short time Fourier transform method can effectively detect the local frequency characteristics of fault signal by inner product. Bao et al. [2] proposed an adaptive short time Fourier transform based on fast path optimization, and applied the method to the fault detection of planetary gearbox. This method can adaptively change time window length in the short-time Fourier transform process. Experimental results show that the adaptive short-time Fourier transform method is effective in planetary gearbox fault diagnosis. Chen [3] proposed a gear tooth fault diagnosis based on wavelet transform. This method successfully extracted fault signal from vibration waveform signal of gear box system. However, there are still some shortcomings of wavelet function, such as the base function is difficult to match with the extracted fault features. Empirical mode decomposition method (EMD) has a good analysis effect on the time-varying nonlinear signals. It has some ability to characterize the local instantaneous characteristics effectively [4]. Tang et al. [5] applied EMD signal decomposition and SVM pattern recognition method in the gear fault diagnosis system. It shows this method accurately identify the gears with different crack depths. In view of the nonstationary characteristics of gear vibration signal, Zhang [6] proposed a fault detection method based on EEMD and SVM for gears. The experimental shows this method is effectively applied to gear fault detection. Although EMD has significant advantages of high time-frequency resolution and strong adaptability compared with other time-frequency analysis methods, there are some defects of EMD, for example: mode aliasing, over envelope which will reduce the fault detection accuracy. LMD can adaptively decompose a chaotic and irregular signal into many PF with physical significance [7]. Cheng et al. [8] proved that LMD method can largely eliminate the endpoint effect and preserve the information contained in the signal more completely. For these advantages, this paper applies LMD in gear compound faults signal decomposition. Wang et al. [9] introduced the mask method into the LMD method, and a LMD-MS method combining the mask signal method was proposed. LMD was used to decompose the signal, and then the mask signal method was used to process the PF component to reduce the noise and eliminate the mode aliasing.

After LMD decomposition, the entropy should be obtained to reflect different fault status from PF components of LMD. sample entropy (SE), approximate entropy (AE) and fuzzy entropy (FE) are often used to obtain the information entropy of vibration signals [10-12]. Now, permutation entropy, an effective method for identifying abrupt change points, is often applied to extract the features of different faults. Landauskas constructed the patterns of permutation entropy by using non-uniform embedding of the vibration signal and detected the early faults of rolling bearing [13]. Sharma combined permutation entropy and variation mode decomposition to detect gear faults effectively [14]. However, the above methods can only extract the entropy in a single scale. Multiscale analysis can reflect the complexity characteristics and obtain more characteristic information of signals [15,16]. Gao et al. applied multiscale permutation entropy (MPE) and tensor nuclear norm canonical polybasic decomposition in the fault detection of gears [17]. It shows this method can accurately identify the different faults of gear. However, the traditional MPE shows inconsistency since some points in the signals are ignored when the original signal is coarsened. [18]. For this reason, the error and fluctuation of entropy will appear with the increasing of scale factor. IMSPE is proposed to solve the existing shortcomings in this paper. The proposed IMSPE is improved from two aspects based on the MPE: the process of coarsening and the definition of entropy. On this basis, the IMSPE method can be effectively utilized to measure the complexity of gear and extract the key feature vector which contained in PF components of LMD.

The proposed method has some advantages. (1) The comparison and analysis of the IMSPE method with the SE, AE, PE method proves IMSPE has obvious advantages in gearbox fault type recognition. The main reason is that multiscale entropy extraction method can improve the effectiveness of sample features compare with single scale entropy methods. (2) The proposed IMSPE solves the errors and fluctuations of the traditional multiscale entropy through the process of coarsening. For this reason, IMSPE can obtain more effective signal features to distinguish different fault types and extract gearbox fault information more accurately compared with MSE, MFE and MPE.

The structure of this paper is presented as follows: Section 2 introduces LMD signal decomposition method. Section 3 proposes the IMSPE feature extraction method. Section 4 analyzes experiment classification results of IMSPE. Section 5 gives the concludes of this paper.

2. Principle of LMD

LMD is an adaptive decomposition method. The LMD method can decompose the non-stationary signal into a series of PF components and a residual component R. each PF component is the product of an envelope signal and a FM signal. The PF component of any original signal $x (t)$ after decomposition can be expressed as follows:

1) Given any $x (t)$ , find out all the maximum and minimum points $n_{i}$ , and calculate the local mean points $m_{i}$ as follows:

1

m_{i} = \frac{(n_{i + 1} + n_{i})}{2} .

All the local mean points $m_{i}$ are connected by straight lines, and then the moving average method is used to smooth for many times, then, mean function $m_{11} (t)$ can be calculated.

2) All envelope estimation points $a_{i}$ are calculated by Eq. (2), and the envelope estimation function $a_{11} (t)$ can be calculated as in step (1):

2

a_{i} = \frac{(n_{i + 1} - n_{i})}{2} .

3) A new signal $h_{11} (t)$ is calculated when $m_{11} (t)$ is subtracted from the given signal $x (t)$ , as shown in Eq. (3):

3

h_{11} (t) = x (t) - m_{11} (t) .

By dividing $a_{11} (t)$ , we can get $s_{11} (t)$ as follows:

4

s_{11} (t) = \frac{h_{11} (t)}{a_{11} (t)} .

Judge whether the obtained signal $s_{11} (t)$ is pure FM signal. If the envelope function $a_{1 n} (t) = 1$ is satisfied, it means that the obtained signal $s_{11} (t)$ is a pure FM signal. Otherwise, the $s_{11} (t)$ is regarded as the $x (t)$ and steps (1)-(3) until the envelope estimation function $a_{1 (n + 1)} (t) = 1$ of $s_{1 n} (t)$ , that is to say, to ensure $s_{1 n} (t)$ as a pure FM signal:

5

\{\begin{array}{l} h_{11} (t) = x (t) - m_{11} (t), \\ h_{12} (t) = s_{11} (t) - m_{12} (t), \\ ⋮ \\ h_{1 n} (t) = s_{1 (n - 1)} (t) - m_{1 n} (t), \end{array}

\{\begin{array}{l} s_{11} (t) = \frac{h_{11} (t)}{a_{11} (t)}, \\ s_{12} (t) = \frac{h_{12} (t)}{a_{12} (t)}, \\ ⋮ \\ s_{1 n} (t) = \frac{h_{1 n} (t)}{a_{1 n} (t)} . \end{array}

4) The envelope estimation function $a (t)$ of component can be obtained by multiplying all envelope estimation functions obtained in iteration process, as shown in Eq. (6):

6

a_{1} (t) = a_{11} (t) a_{12} (t) \dots a_{1 n} (t) = \prod_{q = 1}^{n} a_{1 q} (t) .

5) The first PF component can be obtained by multiplying the envelope estimation function $a_{1} (t)$ with pure FM signal, which is called PF1 component:

7

P F_{1} (t) = a_{1} (t) s_{1 n} (t) .

6) The PF1 component is subtracted from the original signal $x (t)$ to get a new signal $u_{1} (t)$ . Repeat steps (1)-(5) until the residual component $u_{k}$ is a single component signal:

8

\{\begin{array}{l} u_{1} (t) = x_{1} (t) - P F_{1} (t), \\ u_{2} (t) = u_{1} (t) - P F_{2} (t), \\ ⋮ \\ u_{k} (t) = u_{k - 1} (t) - P F_{k} (t) . \end{array}

After LMD decomposition, the original signal is reconstructed as follows:

9

x (t) = \sum_{p = 1}^{k} P F_{k} (t) + u_{k} (t) .

3. The IMSPE method

3.1. Multiscale PE

PE can effectively measure the complexity of signal. When the signal is no regular, the value of PE is high; otherwise, the value is small. For example, the permutation entropy of white noise is the largest while that of sinusoidal signal is the smallest. MPE is an improvement of PE. It decomposes time series into multi sequence, and then calculate PE of each scale subsequence, and then describe the complexity of signals from multiple dimensions. Given time series $x (i)$ , one can decompose it into the multiple scales according to the Eq. (10):

10

y^{s} (j) = \frac{1}{s} \sum_{i = (j - 1) s + 1}^{j s} x_{i} .

In this Formula: $s$ is the scale factor, $1 \leq j \leq n / s$ , $y^{s}$ is a sub-sequence under scale $s$ . For any sub-sequences $y^{s}$ , the MPE is calculated by the following steps:

1) The phase space is reconstructed according to the following formula:

11

Y^{s} = [\begin{array}{l} y^{s} (1) & y^{s} (1 + τ) & \dots & y^{s} (1 + (m - 1) τ) \\ y^{s} (2) & y^{s} (2 + τ) & \dots & y^{s} (2 + (m - 1) τ) \\ y^{s} (3) & y^{s} (3 + τ) & \dots & y^{s} (3 + (m - 1) τ) \\ ⋮ & ⋮ & ⋮ & ⋮ \\ y^{s} (K) & y^{s} (K + τ) & \dots & y^{s} (K + (m - 1) τ) \end{array}] .

In this formula: $Y^{s}$ is the reconstruction matrix. $K = \frac{n}{s} - (m - 1) τ$ , $τ$ is time delay, $m$ is the embedding dimension.

2) Each row $Y^{s} (i)$ of the reconstructed matrix $Y^{s}$ is arranged by ascending order. PE of sub-sequence under the scale $s$ is calculated according the following Eq. (9).

Each row $Y^{s} (i)$ of the reconstructed matrix $Y^{s}$ is presented as follows:

12

y^{s} (i + (j_{1} - 1) τ) \leq y^{s} (i + (j_{2} - 1) τ) \leq \dots \leq y^{s} (i + (j_{m} - 1) τ) .

Therefore, a set of symbolic sequences $S (i)$ can be obtained:

13

S (i) = (j_{1}, j_{2}, \dots, j_{m}) .

In the formula, the $m$ kinds of symbol sequences $j_{1}, j_{2}, \dots, j_{m}$ have $m!$ combinations in total. The sequence of symbols $S (i)$ is one of the permutations of species. By calculating the probability of the occurrence $p_{1}, p_{2}, \dots, p_{k}$ , $k \leq m!$ , the entropy of $k$ different symbol sequences of time series can be defined as permutation entropy as follows:

14

H_{p} (x) = \sum_{j = 1}^{k} - p_{j} l n p_{j} .

3) By calculating the probability of the occurrence of each symbol sequence $p_{1}, p_{2}, \dots, p_{k}$ , $k \leq m!$ , the entropy of $k$ different symbol sequences of time series can be defined as permutation entropy as follows:

15

H_{p} (x) = \sum_{j = 1}^{k} - p_{j} l n p_{j} .

4) Further, the multiscale permutation entropy of the original time series can be obtained by calculating the permutation entropy of the subsequences under other scales according to the above steps.

3.2. The proposed IMSPE

In fact, the multiscale permutation entropy method is widely used in many fields because it can extract the effect feature to represent the state of the system. However, this method still has some drawbacks [17], especially: when the original signal is coarsened, the traditional multiscale permutation entropy algorithm shows inconsistency. For example, when the time scale is 2, the computational model is the same for non-overlapping data points $(x_{1}, x_{2})$ and $(x_{3}, x_{4})$ , but there is no overlapping point such as point $(x_{2}, x_{3})$ . Because there is no calculation model for overlapping cases, it is equivalent to form a breakpoint at this point, which causes a sudden change in the calculation results. In order to solve the above problems, the classical multiscale permutation method is improved from two aspects: the coarsening process and the definition of sample entropy, and then IMSPE is developed to describe the complexity of the signal. The improved coarsening process is shown:

1) Establish a new time series set $z_{i}^{(s)} = \{y_{i, 1}^{(s)}, y_{i, 2}^{(s)}\}$ according to Eq. (16). For each scale factor $s$ , different time series $z_{i}^{(s)} | (i = 1,2, \dots, s)$ can be generated as the Eq. (13), which can optimize the stability of the entropy value at the breakpoint in the traditional method. Since $z_{i}^{(s)}$ is only set as $y_{i, 1}^{(s)}$ , a certain mutation is likely to take place at the breakpoint, which leads to the unstable result of the entropy value in the traditional MPE:

16

z_{i}^{(s)} = \{y_{i, 1}^{(s)}, y_{i, 2}^{(s)}\},

y_{i, 1}^{(s)} = \frac{\sum_{k = (j - 1) s + 1}^{j s} x_{k}}{s},

y_{i, 2}^{(s)} = \frac{\sum_{k = (j - 1) s + 2}^{j s - 1} x_{k}}{s}, i = 1,2, \dots s, j = 1,2, \dots, \frac{n}{s} .

2) In the range $1 \leq i \leq s$ , the probability of each symbol sequence $p_{^{1, i}}^{1}, p_{^{2 i}}^{1}, \dots, p_{_{m!, i}}^{1}$ and $p_{^{1, i}}^{2}, p_{^{2 i}}^{2}, \dots, p_{_{m!, i}}^{2}$ .

3)The IMSPE algorithm is defined as:

17

H_{p}^{i} (x) = \frac{\sum_{f = 1}^{2} \sum_{j = 1}^{m!} - p_{j, i}^{f} l n p_{j, i}^{f}}{2}, 1 \leq i \leq s .

The proposed IMSPE algorithm can solved the problem of non-overlapping data points effectively due to the above improvement.

4. Experiment

4.1. Introduction to the experiment

The gear fault vibration signals are collected through QPZZ-II gear fault test platform which is shown in Fig. 1. This experimental system consists of AC motor, gearbox, loading device, data acquisition system et al. The motor drives the driving shaft in the gearbox. The speed is set at 880 r/min and the sampling frequency is 5120 Hz. In this gearbox, there are two gears meshing with each other, the number of teeth for the small gear is 55, and the number of teeth for the big gear is 75. The small gear is connected with the driving shaft, and the big gear is connected with the driven shaft through the key. The small gear is the driving wheel, and the big gear is the driven wheel. The driven shaft is connected with the magnetic powder brake through the coupling, and the motor speed and load of the magnetic powder brake are controlled by the console. The data acquisition system is composed of acceleration sensor and acquisition instrument.

Fig. 1QPZZ-II gear fault test platform

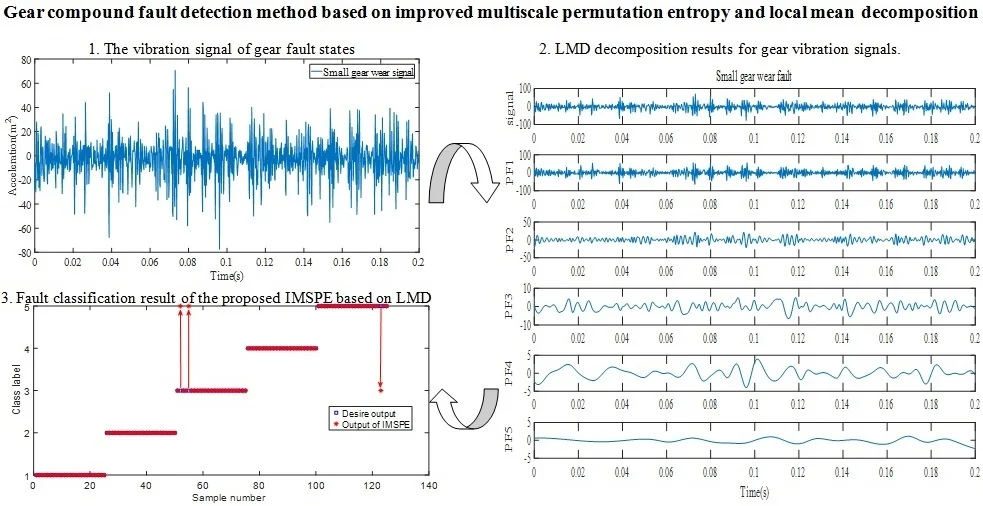
In this experiment, there are five fault types including small gear wear fault, big gear pitting fault, big gear broken tooth fault, big gear pitting+small gear wear fault, big gear broken tooth+small gear wear fault. The latter two faults are compound faults. Two fault gears are presented as in Fig. 2. Vibration signals of five different operating states are shown in Fig. 3.

Fig. 2a) The broken tooth gear and b) wear gear

a)

b)

Due to the influence of random factors such as noise in the signal, the signal component is complex and the fault characteristics are not obvious. It is impossible to distinguish the different gears by directly observing the original time-domain signal type. Based on the proposed IMSPE and LMD, the process of gearbox fault type identification method is presented as follows:

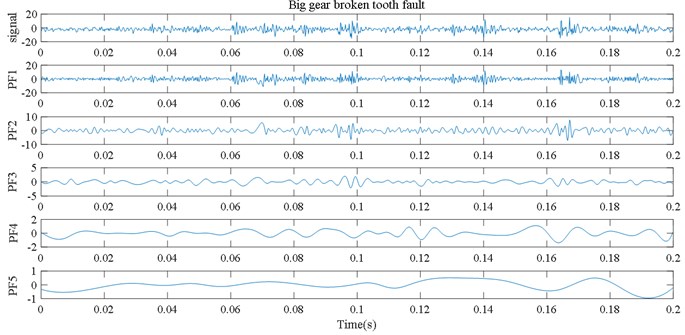
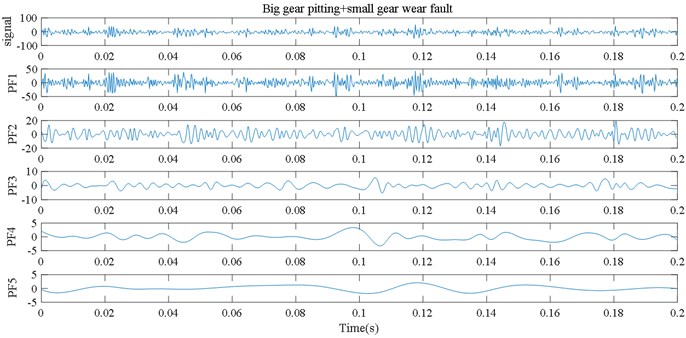
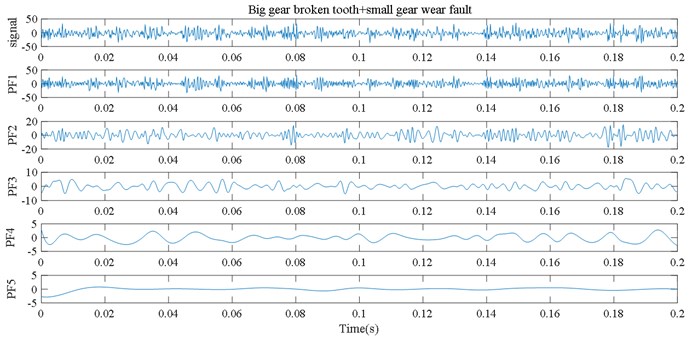
(1) The collected gear fault signals are randomly divided into training set and test set, and a series of PF components are obtained by LMD decomposition. The PF components under five fault states are shown in Fig. 4.

(2) The IMSPE values are calculated from the PF components. In this paper, three parameters of IMSPE are set as follows: data length is $n = 1024$ , embedding dimension $m = 4$ and time delay $τ = 1$ , Scale factor $s = 10$ .

(3) The feature vector obtained from the training set is input into Least squares support vector machines (LSSVM) [19] for training, and the fault type recognition model is obtained. Then, the feature vector obtained from the test set is input LSSVM for fault type identification.

Fig. 3The vibration signal of five fault states

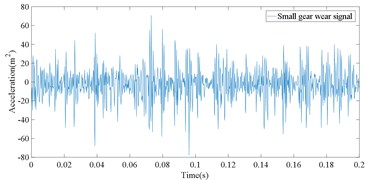
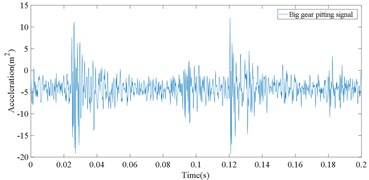
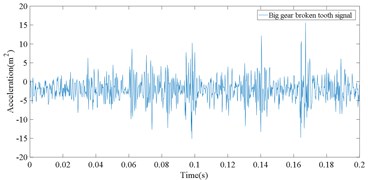
Fig. 4LMD decomposition results for five kinds of gear vibration signals

4.2. Comparative analysis of MSE, MFE, MPE and the proposed IMSPE based on LMD

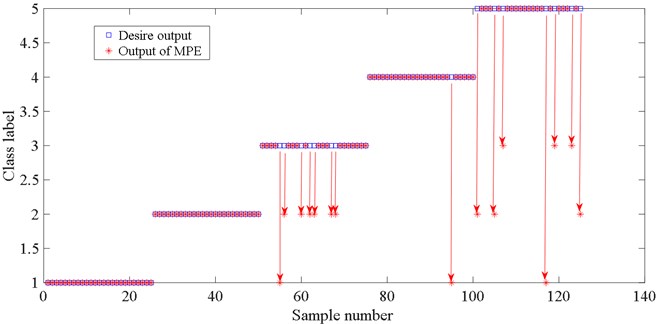
In order to verify the superiority of the proposed IMSPE in feature extraction, some multi scale feature extraction methods, such as multiscale sample entropy (MSE), multiscale permutation entropy (MPE), multiscale fuzzy entropy (MFE), are used to extract the fault features. The scale factor of all these methods is also set 10. For each fault type, there are 40 samples for each fault type. 50 % of the samples were randomly selected for training and the rest for testing. The recognition results based on LSSVM are shown in Figs. 5-8. As can be seen from Fig. 5, only 3 test samples of the proposed IMSPE are misclassified: Two big gear broken tooth faults are mistakenly classified as big gear broken tooth+small gear wear compound faults. One big gear broken tooth+small wear compound fault is wrongly classified as big gear broken tooth fault. All five faults classification results are presented in Table 1.

Table 1Gear fault classification accuracy comparison of four methods

Fault type	Fault output	LMD_MSE	LMD_MFE	LMD_MPE	LMD_IMSPE
Small gear wear fault	1	100 %	96 %	100 %	1000 %
Big gear pitting fault	2	92 %	92 %	100 %	100 %
Big gear broken tooth fault	3	80 %	88 %	72 %	92 %
Big gear pitting +small gear wear fault	4	92 %	96 %	96 %	100 %
Big gear broken tooth+ small gear wear fault	5	72 %	80 %	72 %	96 %

The recognition rate based on IMSPE feature extraction method is 100 %, 100 %, 92 %, 100 %, 96 % for five gear fault samples. Fig. 6 shows the fault classification result of MSE based on LMD. There are 16 test samples of MSE are misclassified. Especially, six big gear broken tooth+small gear wear compound faults are wrongly classified big gear broken tooth faults. One big gear broken tooth+small gear wear compound fault is wrongly classified small gear wear fault. The recognition rate based on MSE feature extraction method is only 100 %, 92 %, 80 %, 100 %, 72 % for five gear fault samples. Fig. 7 shows the fault classification result of MFE based on LMD. There are 12 test samples of MFE are misclassified. Five big gear broken tooth+small gear wear compound faults are wrongly classified big gear broken tooth faults. The recognition rate based on MFE feature extraction method is only 96 %, 92 %, 88 %, 96 %, 80 % for five gear fault samples. Fig. 8 shows the fault classification result of MPE based on LMD. there are 15 test samples of MFE are misclassified. The recognition rate based on MPE feature extraction method is only 96 %, 92 %, 88 %, 96 %, 80 % for five gear fault samples. Through the above comparative analysis, the proposed IMSPE feature extraction method obtain the highest recognition rate. The main reasons is that the traditional multiscale entropy algorithm, such as MPE, MFE, MSE, shows inconsistency since some points in the signals are ignored. The proposed IMSPE solves the errors and fluctuations of MPE, MFE, MSE through the process of coarsening. The fault features, which are obtained by IMSPE, can reflect different fault states of rolling bearing more clearly, so it has higher fault diagnosis accuracy.

Fig. 5Fault classification result of the proposed IMSPE based on LMD

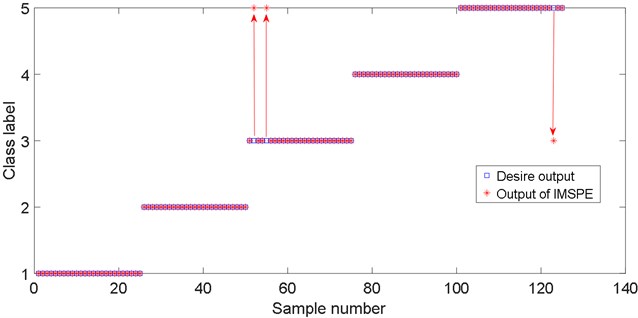
Fig. 6Fault classification result of MSE based on LMD

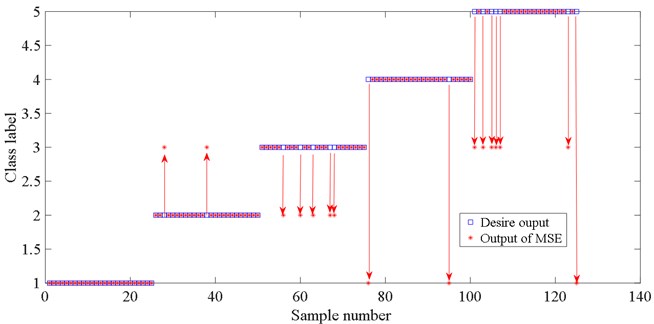
Fig. 7Fault classification result of MFE based on LMD

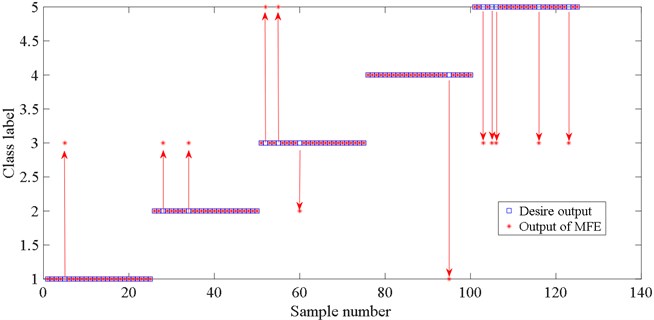
Fig. 8Fault classification result of MPE based on LMD

4.3. Comparative analysis of IMSPE based on LMD and IMSPE for original signal

In order to further verify the necessity of LMD vibration signal decomposition method, the IMSPE value of each PF component obtained by LMD decomposition is compared with the IMSPE value directly calculated from the original signal. The classification results of the five fault types are shown in Fig. 9 and Table 2. The results obtained by directly calculating the IMSPE entropy of the original signal can’t effectively distinguish five types faults of the gearbox. Fig. 9 shows that there are 14 test samples of IMSPE of original signal are misclassified. However, Fig. 3 shows only 3 test samples of IMSPE based on LMD are misclassified. The main reason is that the LMD method decomposes the complex gear non-stationary signal into the sum of several PF components, which highlights the local signal of all kinds of faults, so it can effectively extract the fault features of acoustic emission signal of bearing fault.

Fig. 9Fault classification result of IMSPE value from the original signal

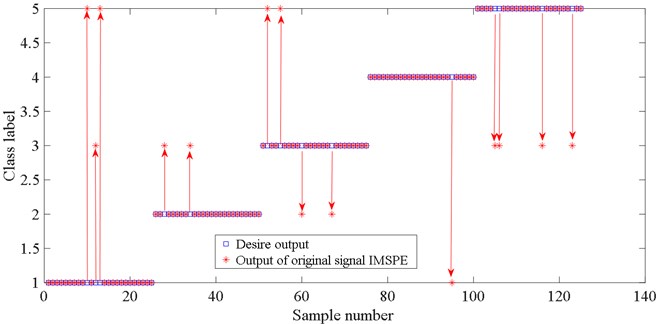
Table 2Gear fault classification accuracy comparison of LMD_IMSPE and Orig_IMSPE

Fault type	Fault output	Orig_IMSPE	LMD_IMSPE
Small gear wear fault	1	88 %	1000 %
Big gear pitting fault	2	92 %	100 %
Big gear broken tooth fault	3	84 %	92 %
Big gear pitting + small gear wear fault	4	96 %	100 %
Big gear broken tooth + small gear wear fault	5	84 %	96 %

4.4. Comparative analysis of SE, AE, PE and the proposed IMSPE based on LMD

In order to verify the advantages of multiscale entropy for IMSPE, single scale entropy methods, such as sample entropy (SE), approximate entropy (AE), permutation entropy (PE) are used to extract the fault features of PF components and input it into the LSSVM for pattern recognition. The number of training samples and test samples is consistent with the IMSPE method, and the entropy of the first five PF components is considered. The classification results of the above five types are shown in Table 3. As can be seen from Table 3, compared with SE, AE and PE, the proposed IMSPE is superior to other three methods and can more accurately distinguish different fault types of gearbox. the main reason is that the multiscale entropy extraction method can improve the effectiveness of sample features compare single scale entropy methods.

Table 3Gear fault classification accuracy comparison of LMD_SE, LMD_AE, LMD_PE and the proposed LMD_IMSPE

Fault type	Fault output	LMD_SE	LMD_AE	LMD_PE	LMD_IMSPE
Small gear wear fault	1	68 %	64 %	84 %	1000 %
Big gear pitting fault	2	80 %	80 %	88 %	100 %
Big gear broken tooth fault	3	60 %	72 %	56 %	92 %
Big gear pitting + small gear wear fault	4	68 %	60 %	100 %	100 %
Big gear broken tooth + small gear wear fault	5	88 %	92 %	60 %	96 %

5. Conclusions

In this paper, a feature extraction method based on LMD and IMSPE is proposed for different fault types of gearbox vibration signals. Compared with MSE, MFE and MPE, the proposed method can extract gear fault information more accurately. In addition, combined with the LSSVM algorithm, the proposed method is realized the fault classification of gear faults. The effectiveness of the method is verified by experiments. The achievements are presented as follows:

1) The proposed IMSPE solves the errors and fluctuations of the traditional multiscale entropy through the process of coarsening. For this reason, IMSPE can obtain more effective signal features to distinguish different fault types and extract gearbox fault information more accurately compared with MSE, MFE and MPE.

2) By studying the five kinds of fault of rolling bearing, it proves that the proposed IMSPE based on LMD can be effectively applied in the compound fault diagnosis of gear.

3) Although with higher fault diagnosis accuracy, the new method still in the experimental verification stage based on the gear experiment system. In terms of this problem, the ability to resist noise should be further improved to make this method more effective in the actual working environment in the future.

References

Y. Lei, J. Lin, M. J. Zuo, and Z. He, “Condition monitoring and fault diagnosis of planetary gearboxes: a review,” Measurement, Vol. 48, pp. 292–305, Feb. 2014, https://doi.org/10.1016/j.measurement.2013.11.012

Publisher
W. J. Bao, X. T. Tu, and F. C. Li, “The adaptive short-time Fourier transform method based on fast path optimization and its application for fault diagnosis of planetary gearbox,” Journal of Vibration Measurement and Diagnosis, Vol. 40, pp. 105–120, 2020, https://doi.org/10.16450/j.cnki.issn.1004-6801.2020.02.009.

Publisher
X. Chen, “Gear tooth fault diagnosis by using order cyclostationary demodulating approach based on chirplet path pursuit,” Journal of Mechanical Engineering, Vol. 48, No. 3, p. 95, 2012, https://doi.org/10.3901/jme.2012.03.095

Publisher
N. E. Huang et al., “The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis,” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, Vol. 454, No. 1971, pp. 903–995, Mar. 1998, https://doi.org/10.1098/rspa.1998.0193

Publisher
Q. Zhao, N. Ye, L. Li, and F. Yan, “Oxalate coprecipitation process synthesis of 5 V cathode material LiNi0.5Mn1.5O4 and its performance,” Rare Metal Materials and Engineering, Vol. 39, No. 10, pp. 1715–1718, Oct. 2010, https://doi.org/10.1016/s1875-5372(10)60130-0

Publisher
J. Wang, P. Jin, P. L. Bishop, and F. Li, “Upgrade of three municipal wastewater treatment lagoons using a high surface area media,” Frontiers of Environmental Science and Engineering, Vol. 6, No. 2, pp. 288–293, Apr. 2012, https://doi.org/10.1007/s11783-011-0280-z

Publisher
J. S. Smith, “The local mean decomposition and its application to EEG perception data,” Journal of The Royal Society Interface, Vol. 2, No. 5, pp. 443–454, Dec. 2005, https://doi.org/10.1098/rsif.2005.0058

Publisher
J.-T. Yuan and T.-C. Lin, “Effects of source distributions on CMA and MMA using symmetric two-dimensional signal constellations,” in MILCOM 2009 – 2009 IEEE Military Communications Conference, Vol. 28, pp. 13–16, Oct. 2009, https://doi.org/10.1109/milcom.2009.5379889

Publisher
Z. J. Wang, W. X. Wu, and W. J. Ma., “Fault signal extraction method of rolling bearing weak fault based on LMd-ms,” Journal of Vibration Measurement and Diagnosis, Vol. 38, pp. 1014–1019, 2018.

Search CrossRef
Z. X. Zhou, Z. J. He, “Fault diagnosis of roller bearings based on ELMD sample entropy and boosting – SVM,” Journal of Vibration and Shock, Vol. 35, No. 18, pp. 190–195, Sep. 2016.

Search CrossRef
S. M. Pincus, “Approximate entropy as a measure of system complexity.,” Proceedings of the National Academy of Sciences, Vol. 88, No. 6, pp. 2297–2301, Mar. 1991, https://doi.org/10.1073/pnas.88.6.2297

Publisher
H. Liu, H. B. Xie, and W. X. He, “Characterization and classification of sleep stage based on fuzzy entropy,” Journal of Data Acquisition and Processing, Vol. 25, pp. 484–489, 2010.

Search CrossRef
M. Landauskas, M. Cao, and M. Ragulskis, “Permutation entropy-based 2D feature extraction for bearing fault diagnosis,” Nonlinear Dynamics, Vol. 102, No. 3, pp. 1717–1731, Nov. 2020, https://doi.org/10.1007/s11071-020-06014-6

Publisher
V. Sharma, “Gear fault detection based on instantaneous frequency estimation using variational mode decomposition and permutation entropy under real speed scenarios,” Wind Energy, Vol. 24, No. 3, pp. 246–259, Mar. 2021, https://doi.org/10.1002/we.2570

Publisher
J. D. Zheng, J. S. Cheng, and S. Y. Hu, “Multiscale entropy based rotor fault diagnosis,” Journal of Vibration Measurement and Diagnosis, Vol. 33, pp. 294–297, 2018.

Search CrossRef
J. D. Zheng, H. Y. Pan, and J. S. Cheng, “Composite Multiscale fuzzy entropy based rolling bearing fault diagnosis method,” Journal of Vibration and Shock, Vol. 35, p. 116, 2016.

Search CrossRef
M. Ge, Y. Lv, C. Yi, Y. Zhang, and X. Chen, “A joint fault diagnosis scheme based on tensor nuclear norm canonical polyadic decomposition and multi-scale permutation entropy for gears,” Entropy, Vol. 20, No. 3, p. 161, Mar. 2018, https://doi.org/10.3390/e20030161

Publisher
X. L. Chen, B. Z. Zhang, and F. Z. Feng, “Fault feature extraction of rolling bearings based on an improved permutation entropy,” Journal of Vibration Engineering, Vol. 31, pp. 902–908, 2018.

Search CrossRef
J. A. K. Suykens, L. Lukas, and J. Vandewalle, Least Squares Support Vector Machines. Singapore: World Scientific, 2002, pp. 757–760.

Publisher

Cited by

Gearbox Fault Diagnosis Based on Refined Time-Shift Multiscale Reverse Dispersion Entropy and Optimised Support Vector Machine

Xiang Wang | Han Jiang

(2023)

Research on fault diagnosis of a railway point machine based on a multi-entropy feature extraction method and support vector machine

Yunting Zheng | Shaohua Chen | Zhiyong Tan | Yongkui Sun

(2023)

Fault Diagnosis of Hydroelectric Units Based on a Novel Multiscale Fractional-Order Weighted Permutation Entropy

Wenjing Zhang | Yuanchen Gao | Shizhe Peng | Dongdong Zhou | Bin Wang

(2022)

Fault Diagnosis Method Based on AUPLMD and RTSMWPE for a Reciprocating Compressor Valve

Meiping Song | Jindong Wang | Haiyang Zhao | Xulei Wang

(2022)

State of the art on vibration signal processing towards data‐driven gear fault diagnosis

(2022)

About this article

Received

29 January 2021

Accepted

03 May 2021

Published

11 August 2021

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2021.21896

Keywords

fault diagnosis

entropy

IMSPE

LMD

Acknowledgements

This research is supported by Public Projects of Zhejiang Province (LGF18F030003) and sponsored by K.C. Wong Magna Fund in Ningbo University.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 01 21

A gear fault diagnosis method based on variational mode decomposition and multi-scale discrete entropy

Tao Zhang, Yongqi Chen, Yang Chen, Qian Shen, Qinge Dai

Research article

2021 03 25

Gearbox fault diagnosis method based on the fusion of EEMD and improved Elman-NN

Xiaobo Zhang

Research article

2019 11 15

Fault diagnosis using an improved fusion feature based on manifold learning for wind turbine transmission system

Ping Ma, Hongli Zhang, Wenhui Fan, Cong Wang

Research article

2018 06 30

The correlation analysis of gear tooth broken-pitting compound fault and single fault based on Laplacian Eigenmaps

Guangbin Wang, Yinghang He, Xiaoyang Du, Long Li, Wenhui Deng

Y. Chen, Y. Chen, and Q. Dai, “Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition,” Journal of Vibroengineering, Vol. 23, No. 5, pp. 1171–1183, Aug. 2021, https://doi.org/10.21595/jve.2021.21896

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2021.21896
UR  - https://doi.org/10.21595/jve.2021.21896
TI  - Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition
T2  - Journal of Vibroengineering
AU  - Chen, Yang
AU  - Chen, Yongqi
AU  - Dai, Qinge
PY  - 2021
DA  - 2021/08/11
PB  - JVE International Ltd.
SP  - 1171-1183
IS  - 5
VL  - 23
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Chen_2021,
	doi = {10.21595/jve.2021.21896},
	url = {https://doi.org/10.21595/jve.2021.21896},
	year = 2021,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	number = {5},
	pages = {1171--1183},
	author = {Yang Chen and Yongqi Chen and Qinge Dai},
	title = {Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Chen, Y. Chen, and Q. Dai, “Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition,” Journal of Vibroengineering, vol. 23, no. 5, pp. 1171–1183, Aug. 2021, doi: 10.21595/jve.2021.21896.

Copy IEEE

Copied to clipboard!

Chen, Yang, Yongqi Chen, and Qinge Dai. “Gear Compound Fault Detection Method Based on Improved Multiscale Permutation Entropy and Local Mean Decomposition.” Journal of Vibroengineering 23, no. 5 (August 11, 2021): 1171–83. https://doi.org/10.21595/jve.2021.21896.

Copy Chicago

Copied to clipboard!

Gear compound fault detection method based on improved multiscale permutation entropy and local mean decomposition

Abstract

Highlights

1. Introduction

2. Principle of LMD

3. The IMSPE method

3.1. Multiscale PE

3.2. The proposed IMSPE

4. Experiment

4.1. Introduction to the experiment

4.2. Comparative analysis of MSE, MFE, MPE and the proposed IMSPE based on LMD

4.3. Comparative analysis of IMSPE based on LMD and IMSPE for original signal

4.4. Comparative analysis of SE, AE, PE and the proposed IMSPE based on LMD

5. Conclusions

References

Cited by

About this article

Related Articles