Abstract
This paper studies the problem of sound propagation above a finite impedance plane. For this purpose, a spherical wave based half-space transfer function with velocity is derived and then is applied in the equivalent source method (ESM) to consider the influence of reflections caused by the finite impedance plane. With the half-space transfer function matching the surface velocity to the equivalent sources, the ESM is applied to estimate the sound filed above a finite impedance plane. Through two numerical simulation experiments, in which two vibrating objects, e.g., an oscillating sphere and a simply supported plate, are respectively used, the proposed model is examined. The results validate that the proposed model is feasible and effective to estimate the sound field above a finite impedance plane.
Highlights
- Equivalent Source Method is used to simulate the sound propagation above a finite impedance plane.
- A spherical wave based half-space velocity transfer function is applied in Equivalent Source Method.
- Half-space Equivalent Source Method can estimate the sound filed above a finite impedance plane exactly.
1. Introduction
Generally, wave propagation types can be examined in different ways. These are: mechanically, acoustically and electromagnetically [1-9]. This work will focus on acoustic waves propagation. A number of scholars had done research on acoustic waves propagation in different environments. Chobeau [1] studied sound propagation through forested areas. In the study, he evaluated the ability of the Transmission Line Matrix method to model sound scattering by cylindrical scatterers. Rabisse [2] simulated sound propagation in a confined environment with the presence of geometrical relief on the room surfaces by combining the Adaptive Rectangular Decomposition method and the Finite-Difference Time-Domain method. Duan [3] proposed an equivalent source formulation of Closed Virtual Impedance Surface (CVIS) and calculated the radiated SPL of a spherical shell in shallow and deep sea. The results verified the efficiency of the model when eliminating the irregular frequency problem in ocean acoustic environment. Avital [4] analysed the sound scattering by an elastic spherical shell and canceled the sound scattering by using multi-pole sources located at the centre of the shell. Li [5] developed an approximate analytical solution of the blasting seismic wave in viscoelastic half space based on the reflection coefficients of plane waves.
These researches developed numerical models while taking account of reflections, scatterings, diffractions, or transmissions under various complex boundary conditions or in complicated acoustic environment. Accordingly, the models are a little or quite complicated. This paper is going to apply a simple model, Equivalent Source Method-based Near-field Acoustic Holography (ESM-NAH) [10-12], to simulate the sound propagation above a finite impedance plane. The NAH is a useful tool to visualize the three-dimensional sound field and the ESM is a method with simple principle and fast calculation speed. The boundary condition involved here is different from the ideal rigid boundary and pressure release boundary, but a very general boundary condition with the acoustic impedance rate between zero and positive infinity in engineering applications.
However, the conventional NAH is only applied to the free sound field. To extend the NAH to a wider range of practical applications, more and more researchers are considering the reflections, transmissions or scatterings in NAH. Kim [13] has done a great deal of research on sound propagation and studied how sound waves are reflected and transmitted when they meet a surface of discontinuity in space. To consider the problem of separating and reconstructing the sound field radiated by a vibrating plate that faces a parallel reflector, Zea [14-15] proposes a Fourier-based technique to process near-field microphone array measurements that are performed on a single plane between the plate and the reflector. Through applying a half-space transfer function to the conventional NAH, Wu [16] used the Inverse Boundary Element Method (IBEM) and Bi [17] used the ESM to realize the reconstruction of the vibrating structures in half space, and Pan [18] reconstructed the transient half-space sound field. These models are based on the plane wave assumption, resulting that it obtains a reasonable accuracy in describing the sound field only when the measuring point is at least half a wavelength away from the impedance plane. Then Bi and Jing [19-20] introduced a spherical wave based half-space transfer function [21-22] which is the exact solution of the sound pressure of a monopole source in the half space into the ESM to reconstruct the normal velocity on the surface of a spherical source and a plate source. Since the spherical wave based half-space transfer function satisfies the boundary impedance condition of the plane automatically, the spherical wave based half-space ESM model shows an excellent performance on reconstructing the vibrating objects.
Inspired by the researches above, this paper is going to develop the application of the spherical wave based half-space transfer function to simulate the sound propagation above a finite impedance plane based on the surface velocity by using the ESM. For simplicity, this model is named half-space ESM.
The procedure of simulating the sound propagation above a finite impedance plane by the half-space ESM can be described as following:
(1) Measure the surface velocity of the source above a finite impedance plane;
(2) Arrange the equivalent sources forming the fictitious surface;
(3) Construct the half-space transfer function between the surface velocity and the equivalent sources on the fictitious surface;
(4) Obtain the strength of the equivalent sources from the surface velocity and the transfer function constructed in step (3);
(5) Construct the half-space transfer function between the sound pressure and the equivalent sources on the fictitious surface;
(6) Estimate the sound pressures in the half-space sound field from the equivalent source strength and the transfer function constructed in step (5).
2. Theoretical background of the half-space ESM
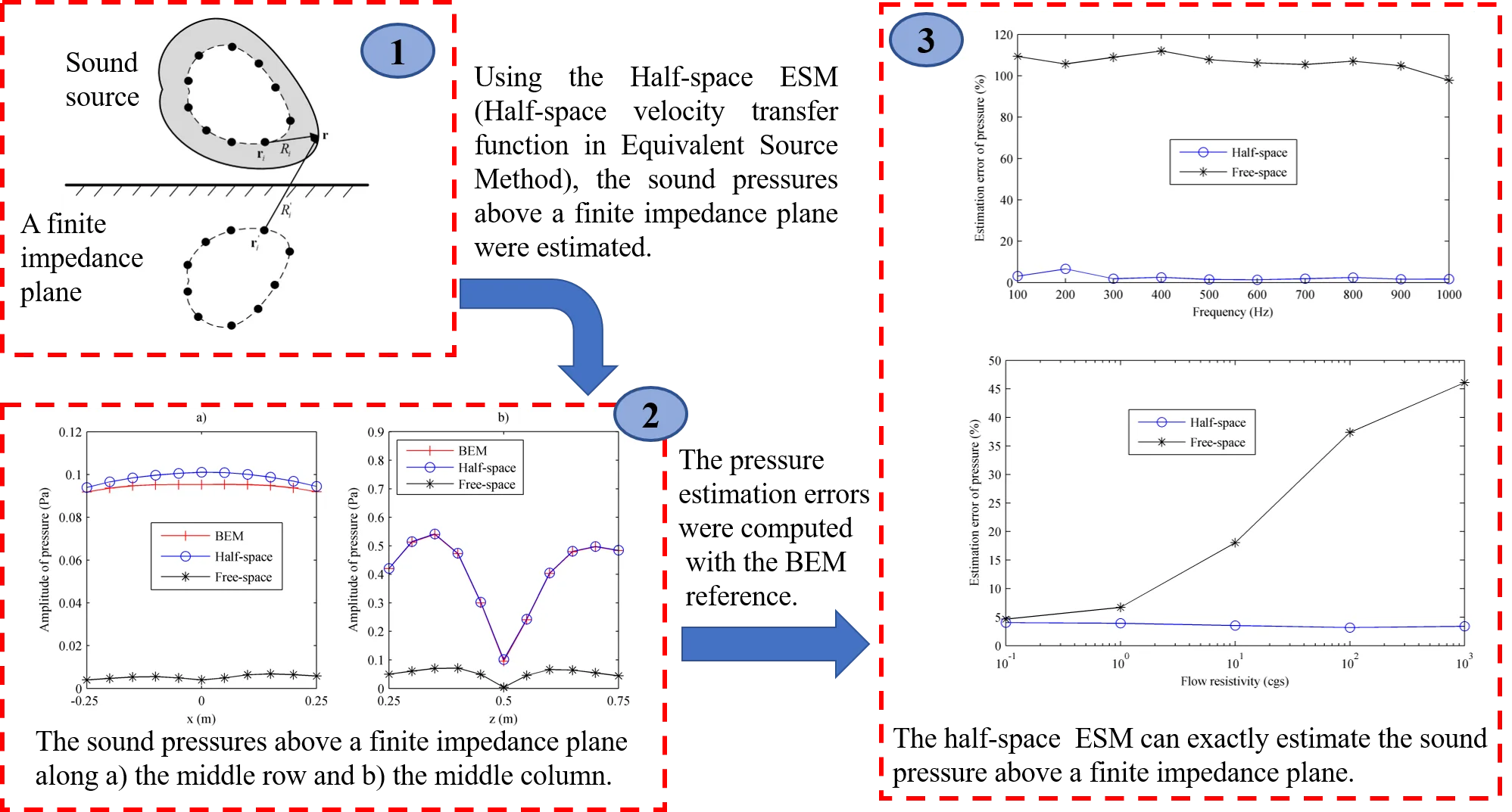
Assuming that a sound source is located above a finite impedance plane, the surface velocity can be expressed as the superposition of sound fields radiated by the equivalent sources arranged within the sound source. Given a surface node of the source indicated in Fig. 1, the normal velocity can be formulated with the equivalent sources and the half-space transfer function with velocity as following:
where and are respectively the strength and location of the th equivalent source, and equivalent sources are arranged within the sound source to form the fictitious surface. The half-space transfer function with velocity, , can be derived by taking the derivative of the half-space transfer function with pressure, which is formulated as [21-22]:
where “” is the imaginary unit with , is the wave number, is the normalized impedance, , , and are the coordinates of the surface node , the th equivalent source , the th image source and the th complex image source , respectively. For more detail, please refer to Ref. s [21-22]. Then the half-space transfer function with velocity can be formulated as:
where “” represents the dot product operator, and represents the unit normal vector on the source surface.
Fig. 1The schematic diagram of the half-space ESM
Considering a series of surface nodes, the normal velocities in Eq. (1) would be a vector and can be formulated as:
where is the transfer function matrix between the surface velocities and the equivalent sources with each element expressed with Eq. (3), and is the source strength vector. With the known surface velocity, the source strength vector can be solved by regularization as:
where is the unit matrix, represents the regularization parameter, “” represents the Hermitian transpose operator, and “–1” represents the inverse operator.
Having obtained the vector , the strength of each equivalent source is available, and then the sound pressure generated by the sound source above a finite impedance plane can be estimated by:
where is a field point in the half-space, and the is the angular frequency. According to Eq. (2), the half-space transfer function with pressure can be formulated easily with replaced with .
3. Numerical simulation experiments
In the numerical simulation experiments, an oscillating sphere and a simply supported plate were used to validate the effectiveness of the proposed half-space ESM model in estimating the sound propagation above a finite impedance plane, respectively. Assuming that the finite impedance plane is the type of Delany and Bazley [23], the normalized impedance would be formulated as:
where is the analysis frequency under research, is the flow resistivity of the finite impedance plane, and is presented in cgs units here.
3.1. An oscillating sphere
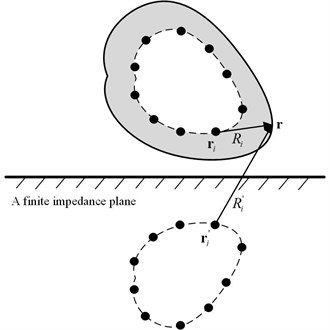
With the finite impedance plane as the plane, a Cartesian coordinate system was established, as shown in Fig. 2. An oscillating sphere with a radius of 0.1 m was located 0.5 m above the impedance plane. The surface of the oscillating sphere was evenly divided into 42 nodes with the interval of /6 and /4 in the polar and azimuth angle direction, respectively. The normal velocity at each node of the oscillating sphere surface was given as:
where is the radial velocity, is the oscillating sphere radius, is the coordinate of the oscillating sphere center, and is the coordinate of the surface node. Here 1 m/s, 0.1 m, 0.5 m. In order to simulate the reality, the Gaussian white noise of 30 dB was brought in the theoretical velocity computed with Eq. (8).
Provided that the finite impedance plane is a patch of grass, the flow resistivity of the finite impedance plane can be set as 35 cgs units. Then the normalized impedance of the plane can be obtained from Eq. (7), and the half-space transfer functions formulated by Eq. (2-3) is available.
To validate the effectiveness of the proposed model, the pressure in the half-space sound field radiated by the oscillating sphere was estimated. The grid points where the pressures were under estimation were distributed on an array , which was perpendicular to the impedance plane and parallel to the plane, as shown in Fig. 2. The central point of the array was in the same horizontal position with the center of the oscillating sphere, and the two center points were 0.2 m apart. The array covered the area of (-0.25 0.25 m, 0.25 0.75 m) with the interval of 0.05 m in both directions.
The equivalent sources were arranged on a concentric spherical surface with a radius of 0.02 m inside the oscillating sphere, as shown in Fig. 2, and the distribution interval was the same as that of nodes on the oscillating sphere surface in angle.
Fig. 2Location of the oscillating sphere and the array F above a finite impedance plane
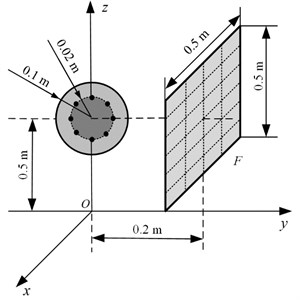
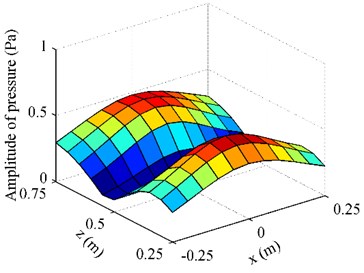
Fig. 3The pressure on F radiated by the oscillating sphere above a finite impedance plane at 500 Hz: a) obtained by using BEM; b) obtained by using half-space ESM; c) obtained by using free-space ESM
a)
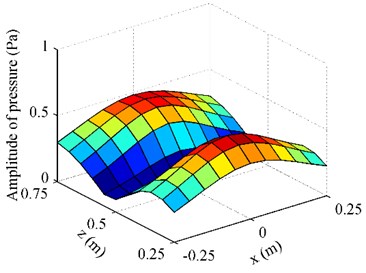
b)
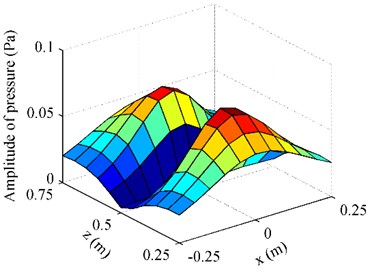
c)
Fig. 3 gives the pressure on radiated by the oscillating sphere above a finite impedance plane at 500 Hz. To examine the performance of the proposed half-space ESM model, the radiation results obtained by using the BEM codes [24-25] were also given in Fig. 3, acting as the reference. Besides,the conventional ESM, i.e. the free-space ESM without consideration the reflection of the impedance plane, was also used to estimate the radiation pressure. From Fig. 3, it can be found that the pressure map obtained by using the half-space ESM was consistent with the reference and the amplitudes of them two were very close, while the pressure map and amplitudes obtained by using the free-space ESM were far from the reference. To show the difference between the three results more clearly, Fig. 4 gives the pressure on along the middle row and the middle column. It can be found that the pressure obtained from the half-space ESM agrees very well with the reference, while the pressure obtained from the free-space ESM is quite different from the reference. These illustrate that the reflection caused by the finite impedance plane should be taken into account and the half-space ESM is feasible and effective to estimate the pressure radiated by the oscillating sphere above a finite impedance plane.
Fig. 4The pressure on F radiated by the oscillating sphere above a finite impedance plane at 500 Hz along a) the middle row and b) the middle column
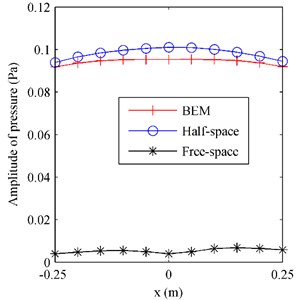
a)
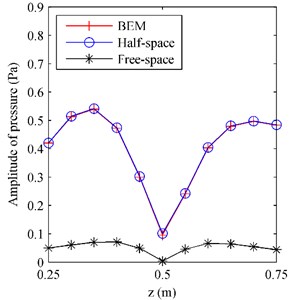
b)
Furthermore, Fig. 5 gives the estimation error of pressure versus the frequency. Here, the estimation error was defined as:
where is the radiation pressure estimated by using the half-space or the free-space ESM and is the reference pressure which is obtained by using the BEM codes. From Fig. 5, it can be seen that the estimation error obtained by using the half-space ESM is quite small, less than 7 %, but the error obtained by using the free-space ESM is very large, above 97 %.
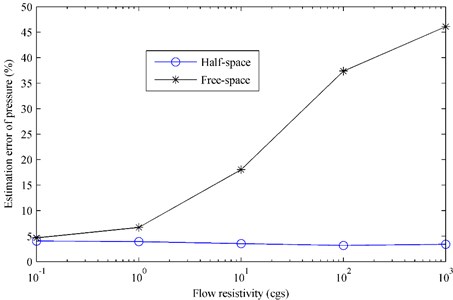
Moreover, Fig. 6 gives the estimation error of pressure in different flow resistivity of the finite impedance plane. It can be found that the estimation error obtained by using the free-space ESM increases as the flow resistivity increases. When the flow resistivity is small, the impedance plane is strongly absorptive, causing little reflection. Under this condition, the influence of the reflection caused by the impedance plane can be neglected, i.e. the sound field can be regard as a free field, thus the free-space ESM can show a good performance. However, the impedance plane becomes less absorptive as the flow resistivity increases, and the reflection grows more and more. Finally, the free-space ESM is gradually failing. By comparison, the half-space ESM always performs well with the estimation errors around 3 % in the whole flow resistivity range.
Both Figs. 5 and 6 verify that it is necessary to consider the reflections caused by the impedance plane and the half-space ESM is able to predict the sound field radiated by an oscillating sphere above a finite impedance plane exactly.
Fig. 5The estimation error of pressure radiated by the oscillating sphere above a finite impedance plane versus the frequency
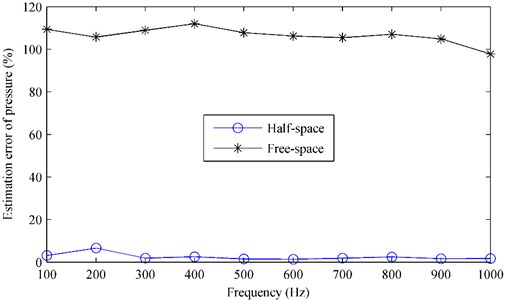
Fig. 6The estimation error of pressure radiated by the oscillating sphere above a finite impedance plane versus the flow resistivity
3.2. A simply supported plate
A simply supported plate was also used to validate the effectiveness of the proposed half-space ESM model. The plate was made of aluminum with the size of 0.3 m×0.3 m and the thickness of 0.005 m. At the center, an incentive force of 10 N was used to drive the plate to cause it vibrate. If the plate instead of the oscillating sphere was putted in Fig. 2, the surface of the plate was exactly in the plane and the center of plate was 0.3 m above the finite impedance plane. According to Ref. [12], the Rayleigh’s integral can be used to compute the normal velocity on the plate surface.
Similarly, the flow resistivity of the impedance plane was still set as 35 cgs units. And the pressure radiated by the plate above the impedance plane was estimated. The array was 0.1 m away from the surface of plate with the same height of the plate center. And the array covered the area of (-0.25 0.25 m, 0.05 0.55 m) with the interval of 0.05 m in both directions.
The equivalent sources were arranged on a planar surface which –0.05 m away from the surface of plate. The planar surface covered the area of (-0.15 0.15 m, 0.15 0.45 m) with the interval of 0.03 m in both directions.
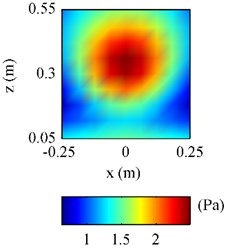
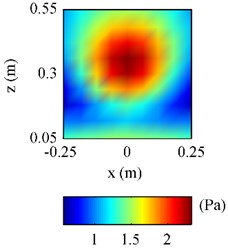
The half-space ESM as well as the free-space ESM was used to estimate the pressure on radiated by the plate above the finite impedance plane at 500 Hz, and the results were given in Figs. 7 and 8. To examine the effectiveness of the half-space ESM, the Rayleigh’s integral was also used to formulated the pressure on , which acted as the reference.
Fig. 7The pressure on F radiated by the plate above a finite impedance plane at 500 Hz: a) obtained by using Rayleigh’s integral; b) obtained by using half-space ESM; c) obtained by using free-space ESM
a)
b)
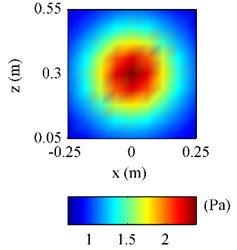
c)
Fig. 8The pressure on F radiated by the plate above a finite impedance plane at 500 Hz along a) the middle row and b) the middle column
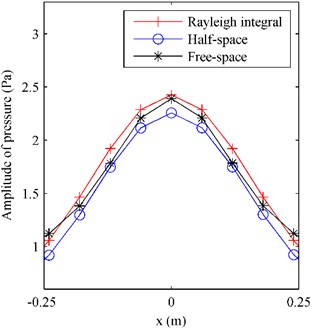
a)
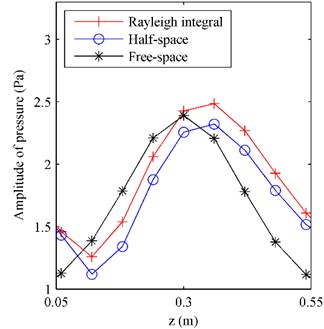
b)
From Fig. 7(a), it can be seen that there are fluctuations at the bottom of reference pressure map, showing that the pressure at the area close to the impedance plane, i.e. 0.1 m, was influenced by the reflections caused by the impedance plane. Observing Fig. 7(b) and 7(c), it can be found the half-space ESM gave a reasonable pressure map showing the influence of the reflections, while the free-space ESM missed the influence of the reflections giving a smooth pressure map. And Fig. 8(b) further verifies that the pressure obtained by using the half-space ESM is much closer to the reference than the pressure obtained by using the free-space ESM.
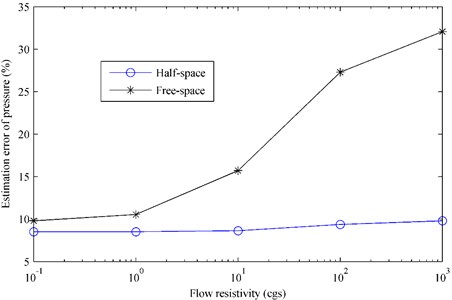
Moreover, Fig. 9 gives the estimation error of pressure versus the frequency and Fig. 10 gives the estimation error versus the flow resistivity. From Fig. 9, it can be seen that the estimation error based on the half-space ESM increases slightly with the increase of frequency but less than 22 %, while the error based on the free-space ESM is much larger, ranging from 30 % to 48 %. Similar to Fig. 6, Fig. 10 also shows that the half-space ESM performs well in the whole flow resistivity range with the errors around 9 %, while the free-space ESM gives larger and larger error as the flow resistivity increases.
These results illustrate that the reflections caused by the finite impedance plane should be taken into account and the half-space ESM is feasible and effective to estimate the sound pressure radiated by a plate source in the half-space field.
Fig. 9The estimation error of pressure radiated by the plate above a finite impedance plane versus the frequency
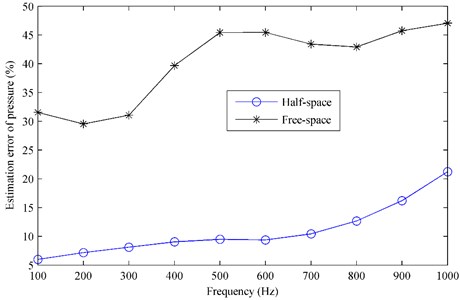
Fig. 10The estimation error of pressure radiated by the plate above a finite impedance plane versus the flow resistivity
4. Conclusions
This paper proposed a half-space ESM model to estimate the sound propagation above a finite impedance plane. In this model, the half-space transfer function which relates the surface velocity or the sound pressure to the equivalent sources was used to consider the influence of reflections caused by the impedance plane. To validate the effectiveness of the proposed model, two numerical simulation experiments were carried out with an oscillating sphere and a simply supported plate respectively used. The results of both experiments suggest that it is necessary to consider the reflections caused by the finite impedance plane and verify that the half-space ESM is able to estimate the sound propagation produced by a source above a finite impedance plane exactly.
Due to limited experimental conditions, this paper did not carry out practicality experimental research. At the moment, the author is trying to join a new laboratory which can provide a wide variety of experimental conditions. Then some practicality experiments would be conducted to do further research about the proposed model.
References
-
P. Chobeau, G. Guillaume, J. Picaut, D. Ecotière, and G. Dutilleux, “A Transmission line matrix model for sound propagation in arrays of cylinders normal to an impedance plane,” Journal of Sound and Vibration, Vol. 389, pp. 454–467, Feb. 2017, https://doi.org/10.1016/j.jsv.2016.11.005
-
K. Rabisse, J. Ducourneau, A. Faiz, and N. Trompette, “Numerical modelling of sound propagation in rooms bounded by walls with rectangular-shaped irregularities and frequency-dependent impedance,” Journal of Sound and Vibration, Vol. 440, pp. 291–314, Feb. 2019, https://doi.org/10.1016/j.jsv.2018.08.059
-
D. Jia-Xi, Z. Lin, S. Xue-Hai, C. Wen-Jing, and D. Liang-Long, “An equivalent source CVIS method and its application in predicting structural vibration and acoustic radiation in ocean acoustic channe,” Ocean Engineering, Vol. 222, p. 108570, Feb. 2021, https://doi.org/10.1016/j.oceaneng.2021.108570
-
E. J. Avital, N. D. Bholah, G. C. Giovanelli, and T. Miloh, “Sound scattering by an elastic spherical shell and its cancellation using a multi-pole approach,” Archives of Acoustics, Vol. 42, No. 4, pp. 697–705, Dec. 2017, https://doi.org/10.1515/aoa-2017-0072
-
Z. Li, H. Li, L. Liu, and H. Zuo, “Propagation of blasting seismic wave in viscoelastic full space and half space under infinitely long cylindrical charge,” Journal of Applied Geophysics, Vol. 181, p. 104137, Oct. 2020, https://doi.org/10.1016/j.jappgeo.2020.104137
-
A. N. Basmact, “Characteristics of electromagnetic wave propagation in a segmented photonic waveguide,” Journal of Optoelectronics and Advanced Materials, Vol. 22, No. 9-10, pp. 452–560, 2020.
-
A. N. B. Filiz, “Solution of Helmholtz equation using finite differences method in wires have different properties along x-axis,” Journal of Electrical Engineering, Vol. 6, No. 4, pp. 206–211, 2018.
-
A. Khurana and S. K. Tomar, “Propagation of plane elastic waves at a plane interface between two electro-microelastic solid half-spaces,” International Journal of Solids and Structures, Vol. 44, No. 11-12, pp. 3773–3795, Jun. 2007, https://doi.org/10.1016/j.ijsolstr.2006.10.018
-
H. Xu and J. Yang, “New design of AOTF using ZnO/LiNbO3 thin-plating surface acoustical waveguide,” Journal of Optoelectronics and Advanced Materials, Vol. 12, No. 7, pp. 1463–1465, 2010.
-
M. R. Bai, J.-H. Lin, and K.-L. Liu, “Optimized microphone deployment for near-field acoustic holography: To be, or not to be random, that is the question,” Journal of Sound and Vibration, Vol. 329, No. 14, pp. 2809–2824, Jul. 2010, https://doi.org/10.1016/j.jsv.2010.01.027
-
G. H. Koopmann, L. Song, and J. B. Fahnline, “A method for computing acoustic fields based on the principle of wave superposition,” The Journal of the Acoustical Society of America, Vol. 86, No. 6, pp. 2433–2438, Dec. 1989, https://doi.org/10.1121/1.398450
-
E. G. Williams, Fourier Acoustics: Sound Radiationand Nearfield Acoustical Holography. San Diego: Academic Press, 1999.
-
Y. H. Kim, Sound Propagation: an Impedance Based Approach. Singapore: Wiley, 2010.
-
E. Zea and I. Lopez Arteaga, “Single layer planar near-field acoustic holography for compact sources and a parallel reflector,” Journal of Sound and Vibration, Vol. 380, pp. 129–145, Oct. 2016, https://doi.org/10.1016/j.jsv.2016.06.012
-
E. Zea and I. L. Arteaga, “Sound field separation for planar sources facing a parallel reflector,” Applied Acoustics, Vol. 149, pp. 181–191, Jun. 2019, https://doi.org/10.1016/j.apacoust.2019.01.030
-
X. Zhao and S. F. Wu, “Reconstruction of vibroacoustic fields in half-space by using hybrid near-field acoustical holography,” The Journal of the Acoustical Society of America, Vol. 117, No. 2, pp. 555–565, Feb. 2005, https://doi.org/10.1121/1.1847994
-
C. X. Bi, X. Z. Chen, R. Zhou, and J. Chen, “Reconstruction and separation in a semi-free field by using the distributed source boundary point method-based nearfield acoustic holography,” Journal of Vibration and Acoustics, Vol. 129, No. 3, pp. 323–329, Jun. 2007, https://doi.org/10.1115/1.2731403
-
S. Pan, W. Jiang, H. Zhang, and S. Xiang, “Modeling transient sound propagation over an absorbing plane by a half-space interpolated time-domain equivalent source method,” The Journal of the Acoustical Society of America, Vol. 136, No. 4, pp. 1744–1755, Oct. 2014, https://doi.org/10.1121/1.4895705
-
C.-X. Bi, W.-Q. Jing, Y.-B. Zhang, and W.-L. Lin, “Reconstruction of the sound field above a reflecting plane using the equivalent source method,” Journal of Sound and Vibration, Vol. 386, pp. 149–162, Jan. 2017, https://doi.org/10.1016/j.jsv.2016.09.029
-
W.-Q. Jing, H. Wu, and J.-Q. Nie, “Optimization of equivalent source configuration for an independent-equivalent source method in half-space sound field,” Shock and Vibration, Vol. 2020, pp. 1–9, Mar. 2020, https://doi.org/10.1155/2020/6029393
-
X. Di and K. E. Gilbert, “An exact Laplace transform formulation for a point source above a ground surface,” The Journal of the Acoustical Society of America, Vol. 93, No. 2, pp. 714–720, Feb. 1993, https://doi.org/10.1121/1.405435
-
M. Ochmann, “The complex equivalent source method for sound propagation over an impedance plane,” The Journal of the Acoustical Society of America, Vol. 116, No. 6, pp. 3304–3311, Dec. 2004, https://doi.org/10.1121/1.1819504
-
M. E. Delany and E. N. Bazley, “Acoustical characteristics of fibrous absorbent material,” The Journal of the Acoustical Society of America, Vol. 48, No. 2A, pp. 434–434, Aug. 1970, https://doi.org/10.1121/1.1912158
-
H. Brick and M. Ochmann, “A half‐space BEM for the simulation of sound propagation above an impedance plane,” The Journal of the Acoustical Society of America, Vol. 123, No. 5, pp. 3418–3418, May 2008, https://doi.org/10.1121/1.2934160
-
S. Marburg, B. Nolte, R. Bernhard, and S. Wang, Computational Acoustics of Noise Propagation in Fluids: Finite and Boundary Element Methods. Berlin, Heidelberg: Springer-Verlag, 2008.
About this article
This work was supported by the National Natural Science Foundation of China (Grant No. 11704110), Hubei Superior and Distinctive Discipline Group of “Mechatronics and Automobiles” (XKQ2021011).
