Abstract
In order to improve the stability of the belt conveyor system, its lumped parameters are analyzed and controlled based on the belt conveyor model and the adaptive control algorithm of the fuzzy control. The effect of the parameters on the running deviation mechanism of the belt conveyor is evaluated. Then, the eccentricity of the platen roller () is controlled to reduce the horizontal force and horizontal velocity of the belt conveyor. The research results show that the stability of the belt conveyor is greatly influenced by the eccentricity of the platen roller, especially with the high load and velocity of the belt conveyor. Additionally, with the eccentricity of the platen roller controlled by the fuzzy control, both the horizontal force and horizontal velocity are insignificantly changed when increasing the eccentricity of the platen roller, especially at 0-6°, Therefore, the stability of the belt conveyor system is obviously improved by using the fuzzy control.
Highlights
- The lumped parameters of the belt conveyor system are analyzed and controlled based on the belt conveyor model and the adaptive control algorithm of the fuzzy control to improve the stability of the belt conveyor system.
- The eccentricity of the platen roller (α) is controlled to reduce the horizontal force and horizontal velocity of the belt conveyor.
- The research results show that the stability of the belt conveyor is greatly influenced by the eccentricity of the platen roller.
- Additionally, with the eccentricity of the platen roller controlled by the fuzzy control. both the horizontal force and horizontal velocity are insignificantly changed when increasing the eccentricity of the platen roller, especially at α = 0 - 6 degree.
1. Introduction
To strongly promote green development, belt conveyor systems are widely used in the fields of transporting goods and construction materials in factories, factories, especially the transport of single materials. At present, higher capacity, longer distance, higher speed, and higher precision are the main development direction of the belt conveyor systems. With the increase in transport distance, velocity, and load, the eccentricity problems of the belt conveyor become more serious. The eccentricity of the belt conveyor is the phenomenon of the belt conveyor’s centerline in the direction of the conveyor length deviating from the centerline of the platen roller [1-3]. This is the most common problem during the operation process of the belt conveyor. It can increase the operating resistance and make the material to be damaged. When there is a serious deviation, it can tear the belt conveyor and must stop the production, so it has a significant impact on economic efficiency [1, 3]. A model of horizontal dynamics of the belt conveyor is established to study the deflection of the belt conveyor, and the numerical simulation method is then used to approximate the system’s equation of state and obtain the maximum deflection [4]. A tire theory model is also applied to analyze the forces of the platen roller to improve the friction loss between the platen roller and belt conveyor [2]. The characteristics of the horizontal dynamics of the belt conveyor under different working conditions are simulated and analyzed via the numerical simulation method [3, 5]. The research results show that the dynamic parameters of the belt conveyor system greatly affect the stability and reliability of the platen roller. Based on the research results, the belt conveyor deflection and the optimum design are then also considered.
Based on the different deviation laws in the motion of the platen roller, a situ correction mechanism for the deviation force magnitude between the platen roller and belt conveyor has been designed [6]. An electromechanical device improved based on a gear actuator to correct conveyor deflection in comparison to an existing auto-calibrator is also designed by the fuzzy control technology [7]. Besides, the control of the stability system and the detection of the belt conveyor tear are also studied on laser technology [8, 9]. The research results have greatly improved the working efficiency of the belt conveyor transmission system. However, most scholars mainly focus on the causes of the belt conveyor deflection.
Nowadays, the belt conveyor system is developed in the direction of larger capacity, longer distance, higher speed, and higher precision, therefore, the effect of the eccentricity problem of the belt conveyor is also greater. Consequently, an in-depth study of the belt conveyor deflection mechanism and the control of the conveyor’s motion stability at higher velocities are essential. Only in this way, the horizontal force, friction force, and working efficiency of the belt conveyor can be improved, thus, the operating costs of the belt conveyor can be reduced.
In this study, based on the actual structure of the belt conveyor system, its lumped parameter model is established to analyze the characterizations of the running deviation mechanism of the belt conveyor. The effect of the belt conveyor velocity, dynamic load, and eccentricity of the platen roller on the stability of the belt conveyor is studied. To improve the stability of the belt conveyor stability, the eccentricity of the platen roller is then controlled based on a fuzzy adaptive controller. The reduction of the horizontal force and the horizontal velocity of the belt conveyor is the study goal.
2. The modeling of the belt conveyor system
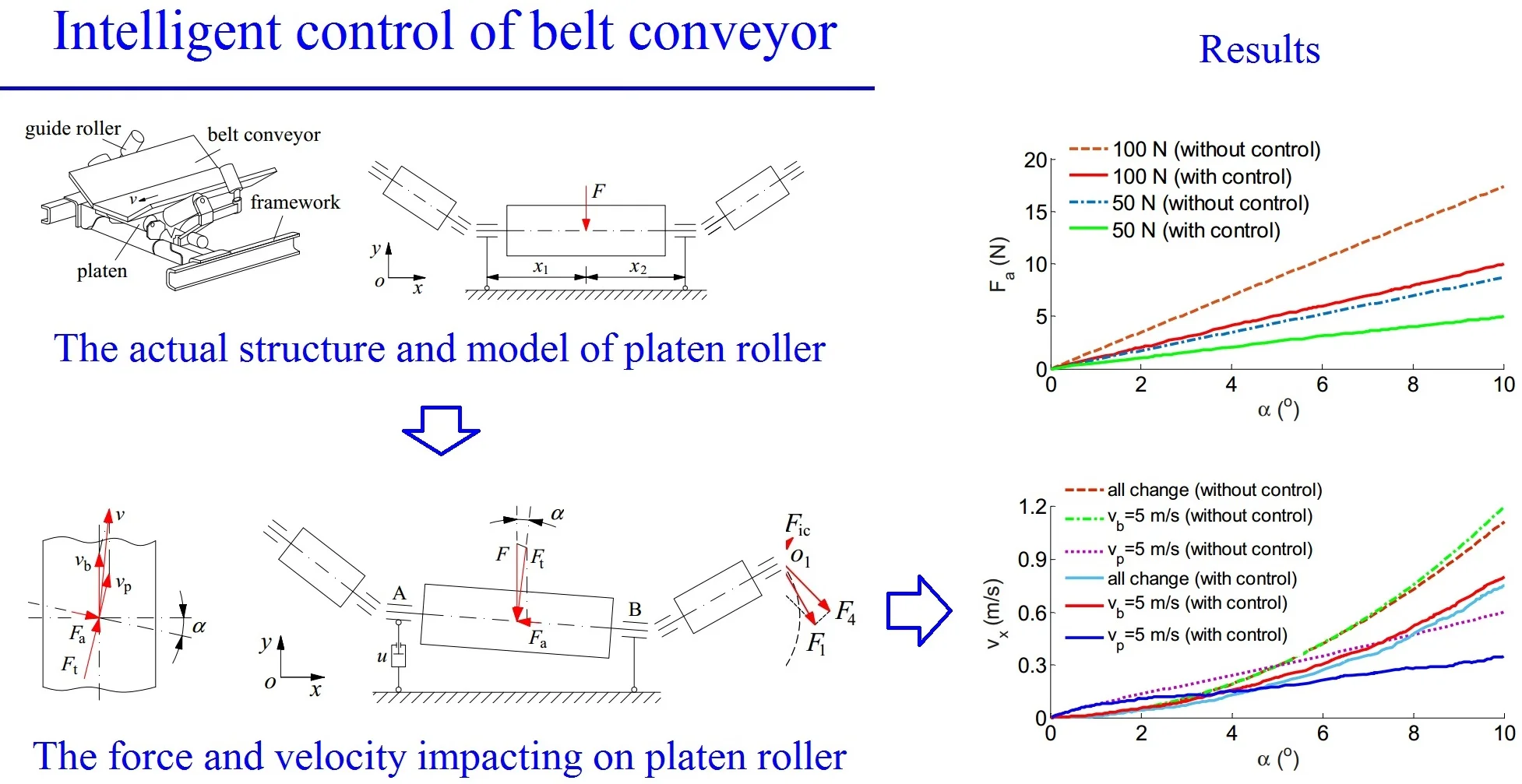
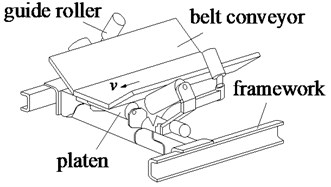
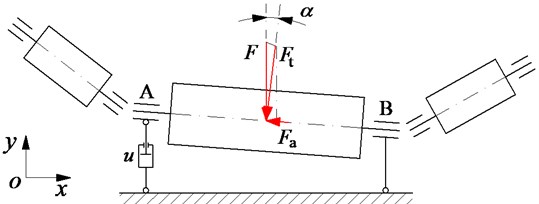
The belt conveyor system including the platen roller used to drive the conveyor, two rollers used to guide movement of the belt conveyor, a belt conveyor used to convey materials, as plotted in Fig. 1. Besides, the force and velocity models are also shown in Fig. 2.
Fig. 1The actual structure and model of the platen roller model
a) The actual structure
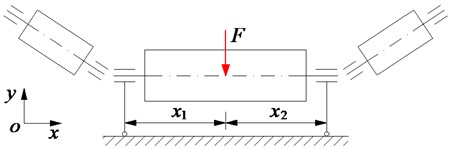
b) The platen roller system model
Fig. 2The force and velocity impacting on the platen roller system: a) the impacting velocity and force on the belt conveyor, b) the impacting force on the platen roller
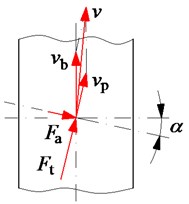
a)
b)
In Fig. 2 is the velocity of the belt conveyor; and are the tangent velocities of the belt conveyor and platen roller; is the dynamic load defined as the mass of the material on the belt conveyor acting on the platen roller, and are the tangent force and axial force of the belt conveyor.
In the ideal operation condition without the dynamic load , the eccentricity of the platen roller is zero, whereby the horizontal force components of the platen roller and belt conveyor are zero, and . However, under various dynamic loads of materials on the belt conveyor impacting on the platen roller, the eccentricity of the platen roller may not be zero. Therefore, the horizontal force and velocity of the platen roller and belt conveyor generated instability for the system are determined as follows.
Under the impact of the dynamic load , assuming that the eccentricity of the platen roller is , thus the force components of and are calculated by:
Herein, the horizontal force of the platen roller tends to push the belt conveyor in the axial direction and causes the instability of the belt conveyor. Thus, the velocity of the belt conveyor is affected by the eccentricity of the platen roller and determined as follows:
The motion velocity of the belt conveyor is calculated by [5]:
The angle deviation between and is defined by , thus, the is determined as follows:
Therefore, the horizontal velocity of the belt conveyor in the direction which causes instability is calculated by:
Therefore, both the horizontal force in Eq. (1) and horizontal velocity in Eq. (4) are used to study on running deviation mechanism and intelligent control of the belt conveyor.
3. Characterization of running deviation mechanism of the belt conveyor
To research the characterizations of running deviation mechanism of the belt conveyor, a range of the dynamic parameters of the belt conveyor including {0, 50, 100} N, {0-10} m/s, {0-10} m/s, and {0-10}° are chosen to simulate and analyze the results. The simulation results of the effect of the parameters on the running deviation mechanism of the belt conveyor are indicated in Fig. 3(a) and (b).
The result in Fig. 3(a) shows that the eccentricity of the platen roller has a negligible effect on the under various dynamic loads of the on the belt conveyor, however, the horizontal force is strongly affected by the eccentricity of the platen roller, especially when increasing the dynamic load on the belt conveyor, as shown in Fig. 3(b). Therefore, it implies that the eccentricity of the platen roller increased by a small value is enough to make the belt conveyor movement unstable. The stability of the belt conveyor is not only affected by the horizontal force but also affected by the horizontal velocity .
The result of the effect of the velocity and angle deviation in Fig. 3(c) also shows that the horizontal velocity is quickly increased when the eccentricity of the platen roller is increased under various simulation conditions of the parameters of the and . Thus, with only a small change of the eccentricity of the platen roller, the horizontal velocity also quickly increases and makes the belt conveyor unstable when increasing the belt conveyor velocity. Consequently, the stability of the belt conveyor movement is greatly depended on the eccentricity of the platen roller, particularly under the high dynamic load and velocity of the belt conveyor. To improve the belt conveyor’s stability and performance, the eccentricity of the platen roller should be controlled.
Fig. 3Effect of the parameters on the running deviation mechanism of the belt conveyor: a)-b) the effect of the force and angle deviation, c) the effect of the velocity and angle deviation
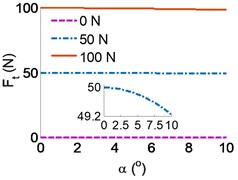
a)
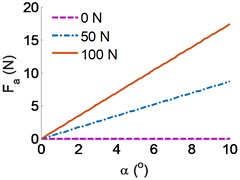
b)
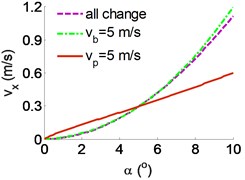
c)
4. Stability control of the belt conveyor
To control the eccentricity of the platen roller , the impacting forces { and } at point A in Fig. 2(b) under the ideal condition ( 0) and actual condition ( 0) are determined by:
Assuming that , the force error between and generated due to the effect of the eccentricity angle is given by:
To reduce the force error , a hydraulic damping mount controlled by the force in the same Fig. 2(b) is used to absorb angle deviations of the belt conveyor based on the change of the dynamic load and feedback signal of . The equation of the control force is calculated by:
To control the force , an adaptive controller of the fuzzy control is then applied. Its control model is designed and shown as in Fig. 4.
The fuzzy control including “a fuzzification interface, a fuzzy inference system, and a defuzzification interface, First, the crisp values in fuzzification are transformed into linguistic variables. The fuzzy inference system is then used by fuzzy rule in accordance with the inference rule. Finally, the linguistic variables are transformed back to crisp values through defuzzification for use by the physical plant”, as found in Ref. [4, 5]. In Fig. 4, the angle deviations and dynamic load are feedback signals of the fuzzy control is used to calculate and decide the control force in Eq. (7) via the linguistic variables defined in Table 1 and If-then rules listed in Table 2 of the fuzzy control. The shape of the membership function for the variables of in-output is the Triangular function and their values are between 0 and 1.
From Table 2, thirty-six If-then rules are described as follows:
(1) If and then ,
(2) if and VS then ,
....,
(36) if VB and VB then .
The fuzzy inference system is then chosen by the Minimum function and centrer method [4, 5] to calculate the control force.
Fig. 4Stability control model of the belt conveyor
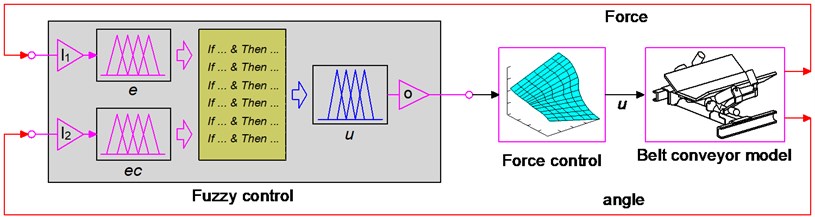
Table 1Fuzzy linguistic values
LV | Description | ec | LV | LV | ||
Z | Zero | 0 | 30 | 0 | Z | |
VS | Very small | 2 | 60 | –0.183 | VS | |
S | Small | 4 | 90 | –1.096 | S | |
M | Medium | 6 | 120 | –3.287 | M | |
B | Big | 8 | 150 | u5 | –7.299 | B |
VB | Very big | 10 | 180 | –13.673 | VB |
Table 2Control rules
Z | VS | S | M | B | VB | ||
Z | |||||||
VS | |||||||
S | |||||||
M | |||||||
B | |||||||
VB | |||||||
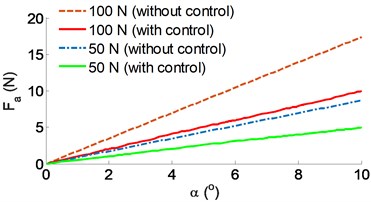
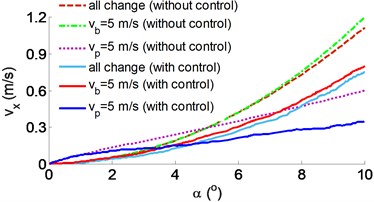
The results of the stability control of the belt conveyor under various simulation conditions are plotted in Fig. 5.
Fig. 5The results of the stability control of the belt conveyor: a) control result of the horizontal force, b) control result of the horizontal velocity
a)
b)
The controlled result of the horizontal force in Fig. 5(a) shows that when the eccentricity of the platen roller is increased, the horizontal force with the control is greatly reduced in comparison without control under two different load conditions of 50 and 100 N on the belt conveyor, especially the value is relatively small at 0-4o. Besides, the controlled result in Fig. 5(b) also indicates that the controlled horizontal velocity is slowly increased with the increase of the eccentricity of the platen roller in comparison without control under various velocities of the and , particularly at 0-6°. Therefore, when the belt conveyor velocity and the eccentricity of the platen roller are increased, the horizontal velocity and the horizontal force are remarkably decreased by the stability control. The result is the stability of the belt conveyor system is improved compared to without control.
5. Conclusions
Based on the actual structure of the belt conveyor system, its lumped parameter model is established to analyze the characterizations of the running deviation mechanism and stability control of the belt conveyor. The research results can be concluded as follows:
1) The stability of the belt conveyor is greatly influenced by the eccentricity of the platen roller, especially with the high load and velocity of the belt conveyor.
2) With the eccentricity of the platen roller controlled by the fuzzy control, both the horizontal force and horizontal velocity are insignificantly changed when increasing the eccentricity of the platen roller, especially at 0-6°, the stability of the belt conveyor system is obviously improved by using the fuzzy control.
References
-
Gabriel F., Vieroslav M., et al., Failure analysis of belt conveyor damage caused by the falling material. Part II: Application of computer metrotomography. Engineering Failure Analysis, Vol. 34, 2013, p. 431-442.
-
Wolpers F. M., Hager M. Tests on the wear behaviour of conveyor belts. Bulk Solids Handling, Vol. 10, Issue 1990, 3, p. 255-264.
-
Mao J., Chen Q. H. Dynamic modeling and simulation of lateral stability belt conveyor. World sci-tech R&D, Vol. 33, Issue 4, 2011, p. 613-616.
-
Yang Y., Miao C., Li X., et al. On-line conveyor belts inspection based on machine vision. Optik, Vol. 125, Issue 19, 2014, p. 5803-5807.
-
Hu K., Wang S., et al. Analysis of lateral force and deviation of permanent magnetic levitation belt conveyor. Journal of System Simulation, Vol. 28, Issue 5, 2016, p. 1173-1178.
-
Li X., Miao C., Wang J., Zhang Y. Automatic defect detection method for the steel cord conveyor belt based on its X-ray images. International Conference on Control, Automation and Systems Engineering (CASE), 2011.
-
Pang Y., Lodewijks G. Large-scale conveyor belt system maintenance decision-making by using fuzzy causal modeling. Proceedings of IEEE Intelligent Transportation Systems, 2005.
-
Phillips D., Lannutti J. Measuring physical density with X-ray computed tomography. NDT&E international, Vol. 30, 1997, p. 339-350.
-
Cui J., Li Y., Ma Z., Lun L., Wang H. Compound motion off-tracking adjusting device for belt conveyor. Coal Mine Machinery, Vol. 39, Issue 7, 2018, p. 104-105.
-
Nguyen V., Jiao R., Zhang J. Control performance of damping and air spring of heavy truck air suspension system with optimal fuzzy control. International Journal of Vehicle Dynamics, Stability, and NVH, Vol. 4, 2020, p. 179-194.
-
Wang P., Nguyen V., Zhang J. Experimental research and optimal control of vibration screed system (VSS) based on Fuzzy control. Journal of Vibroengineering, Vol. 22, Issue 6, 2020, p. 1415-1426.
About this article
This research is supported by Open Fund Project of Hubei Key Laboratory of Intelligent Transportation Technology and Device, Hubei Polytechnic University, China (No. 2020XY105, No. 2020XZ107), Talent Introduction Fund Project of Hubei Polytechnic University (No. 19XJK17R), and the Key Project of Scientific Research Plan of Education Department of Hubei Province (No. 20204501).
