Abstract
We propose a continuous model for rectangular plates that involves a mesh of slender interconnected beams. These beams are disposed orthogonally. The advantage of this model is that simple equations are involved and the behavior of the plate is accurately described. After a brief description of the model, we present an application written in the Python programing language that allows calculating the mode shapes for rectangular plates with various boundary conditions. The mode shapes achieved with the application for a specific plate are found to be similar with those obtained from simulation involving the SolidWorks software. In consequence, we conclude that the proposed model is reliable and the application developed on this base can be used to study the behavior of rectangular plates with different boundary conditions.
1. Introduction
The dynamic behavior of plates was investigated in the past decades by many researchers [1-4], due to their wide-range applications in various fields, such as: aerospace, marine engineering and naval architecture. Thus, Wang and Wereley [5] have proposed analytical solutions for the modal frequencies and displacement mode shapes in a rectangular plate with different boundary conditions, by involving the Kantorovich-Krylov method. Singh and Muhammad [6] carried out a numerical analysis for the free in-plane vibration of a plate with non-rectangular shape. Based on the asymptotic method, Adrianov et al. [7] proposed an analytical solution for the free in-plane vibration of rectangular plates with complex boundary conditions. Further, Boscolo and Banerjee [8] studied the vibration behavior of plates involving the dynamic stiffness method.
As it can be concluded from the above short review, even if the vibration of rectangular thin plates has received a significant amount of researches, there is still potential for innovative approaches. The study presented herein propose a new and simple model for thin rectangular plates, developed for accurate calculus of the mode shapes.
2. Theoretical background
Among the actual approaches to construct the mode shapes for thin rectangular plates fully clamped, that presented in [9] seems to be the simplest. Obviously, for this plate the boundary conditions are realized by hindering the displacement and rotation of the plate edges. The vibration mode function is found in this paper from:
where and are constants to be determined, and are the Bessel function and the modified Bessel function of the first kind of order , respectively. We denoted:
where is the bending rigidity, is the natural frequency, is the mass density, the beam thickness. The bending rigidity is calculated as:
with the Young modulus and the Poisson ratio.
Even if this approach is considered in the literature as simple, it is not easily integrated in a computer program. We solve the problem by developing a simple model that can be adapted easily for any boundary conditions and that makes use of known theories. However, in this study we use the totally clamped plate for exemplification.
In prior research we studied the behavior of beams and plates and have shown that with increasing the beam width this transition is smooth [10]. We also observed that in longitudinal direction the shape of the symmetry axis remains unchanged, irrespective to the width of the structure. In addition, by increasing the width, curving in the transversal direction manifests. First, the shape is a straight line, but with the width increase the curve adopts the shape that corresponds to the first vibration mode. Continuing to increase the beam width, the deformation in the transversal direction becomes similar with mode two and so on. This encouraged us to study the plate as a mesh of orthogonal beams.
The relation to calculate the mode shape of a slender beam is well-known. For a beam fixed at both ends, i.e. fixed-fixed boundary conditions, this relation is:
In the above equation is the distance from the beam end, is the beam length in direction, is the out-of-plain vibration mode number, and is the -th eigenvalue. If considering a beam that is orthogonal to the first one, its mode shapes are expressed:
In this relation is the distance from the beam end, is the beam length in direction, is the out-of-plain vibration mode number, and is the -th eigenvalue. We demonstrate that, for the plate, the displacement in vertical direction can be calculated with the mathematical relation:
The demonstration is made by comparing the shapes achieved with Eq. (6) with those achieved involving numerical simulation. But first, we introduce the PyPLATE application, which we designed to simplify the calculations.
3. The PyPLATE application
To be able to plot rapidly the mode shapes for any combination of mode numbers and , we developed the PyPLATE application, which is written in the Python programming language. It is defined by three classes: “PyPlate”, “Plot”, “PlotNotebook” and some public functions: “OnWord”, “ExtragImageMemory” or “IsNumeric”. The PyPLATE application use the dependencies presented in Table 1.
Table 1Dependencies used by the PyPlate software
Python(x,y) | A free scientific and engineering development software for numerical computations, data analysis and data visualization based on Python programming language | https://python-xy.github.io/ |
Matplotlib | A Python 2D/3D plotting library which produces quality charts | https://matplotlib.org/ |
wxPython | The cross-platform Graphical User Interface toolkit for the Python language | https://wxpython.org/ |
SQLite | A C-language library that implements a small, fast, self-contained, high-reliability, full-featured, SQL database engine | https://www.sqlite.org/ |
numpy | The fundamental package for scientific computing with Python | https://numpy.org/ |
The main window represents a notebook control, which manage three chart windows with the named tabs: “Vibration Plate”, “Shaded” and “Wireframe”. The “Plot” and “PlotNotebook” classes create the main window where the notebook with the chart windows will be created. The public function “ExtragImageMemory”, extracts the icons from database to memory to be used as icons when creating the toolbar.
The application uses a SQLite database to memorize the toolbar icons as image format. These files were loaded as Binaly Large Objects (BLOB) in “Config.db” application’s file.
Fig. 1The „PyPlate” main window with toolbar and “Vibration Plate” chart
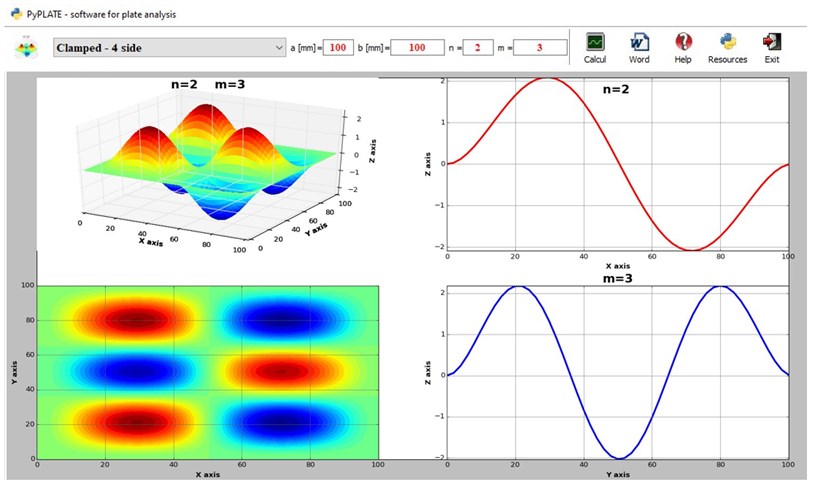
Fig. 1 shows the main window of the application, that has the toolbar located at the top. The toolbar includes controls for plate boundaries selection. It permits the input of the plate dimensions “” and “”, to input vibration mode number “” in the direction and “” in the direction, to activate the calculus and represent the mode shapes derived with Eq. (6). The results in for of graphical representations can be saved to a Word file. One can observe that along with the 3D representation of the plate in bending, the top view and the two projections on the vertical planes are represented. These projections will be compared with the simulation results achieved with the SolidWorks software to validate the proposed model.
In addition to the main window, it is possible to access the “Shaded” chart that is a detailed 3D view of the deformed plate. This view can be rotated around the three axes to have a clear image of the mode shape.
Fig. 2The „PyPlate” main window with toolbar and “Wireframe” chart
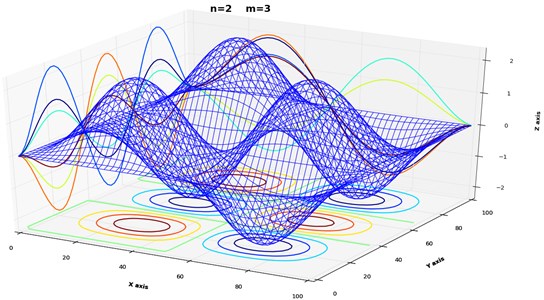
A third chart that is available, the “Wireframe” represented in Fig. 2, shows the mesh of orthogonal beams in deformed state, calculated with Eq. (4) and (5), used to model the plate. This image gives a good description of the proposed model and confirms partially its validity.
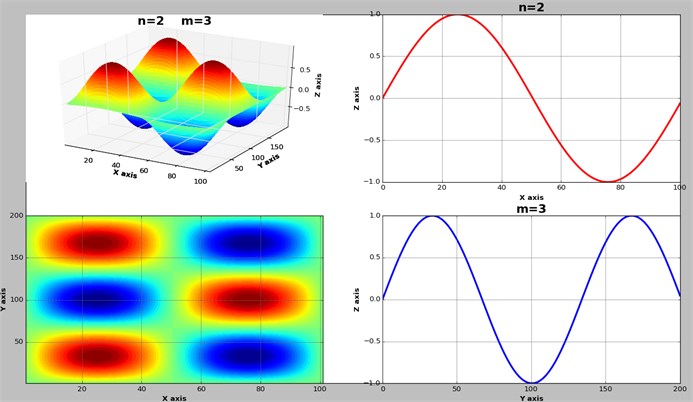
To show how easy it is to find the mode shapes for other boundary conditions by simply selecting the proper mode functions for the two orthogonal beams, in Fig. 3 we represent the case of the plate simply supported at all sides. The complete PyPLATE application can be found on Mendeley datasets, at link [11], and is free to be downloaded.
Fig. 3The four diagrams displayed in the main window of the PyPLATE for a simply supported plate at all sides
4. Validation of the proposed model
To validate the model, we performed several simulations involving the SolidWorks software. The plate modeled here is a steel plate with the dimensions 100 mm×100 mm×0.5 mm. The Alloy Steel material was selected from SolidWorks library with 2.1×1011 N/m2, Poisson ratio 0.28 and mass density 7700 kg/m3. The plate was fixed on all 4 sides, which restraint all translational degrees of freedom to zero. The solid geometry of the plate was meshed with 8383 elements and 16660 nodes to achieve a good resolution.
Fig. 4Comparison of the results obtained with the proposed model implemented in PyPLATE with the results obtained by simulation
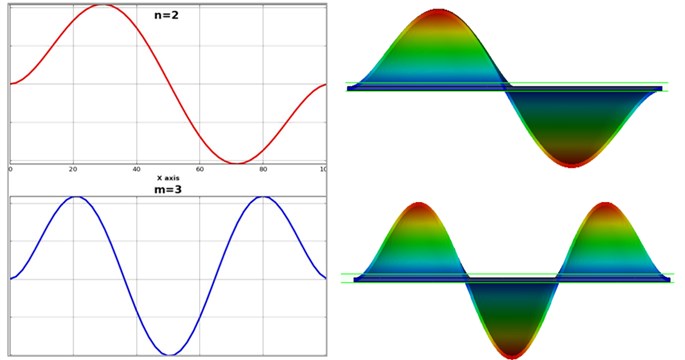
Reviewing Fig. 4, one can observe the perfect fit of the mode shapes drawn with PyPLATE and SolidWorks, which means the model is validated. This good result is obtained for a reasonable ratio between the plate thickness and dimensions and , respectively. This ratio is actually the ratio used to categorize the beam as a Euler-Bernoulli beam. For beams with bigger ratios, the Timoshenko beam model should be considered in the plate model, so in this case Eq. (4) and/or (5) are no longer valid.
Considering the good fit between the shape found by simulation using SolidWorks and that obtained with the proposed model, we can also affirm that the implementation of the model in Python language was made successfully.
5. Conclusions
The paper presents a new model developed for the calculus of the mode shapes of rectangular plates. This model implies using the functions for beams to represent the plate deformation. From numerous experiments it was found the model is very accurate, the mode shapes obtained by using the model (in fact the PyPLATE application) were found to be very similar with those obtained from simulation involving the SolidWorks software.
The plate model can be used for boundary conditions of the plate. with the condition of using the proper beam model in function of its slenderness. Because the shapes used for comparison with SolidWorks involved the PyPLATE application, we concluded that this application is reliable and useful in the study of plates. As a further research direction, we will approach the case of plates with damage in form of structural discontinuities.
References
-
Xing Y., Sun Q., Liu B., Wang Z. The overall assessment of closed form solution methods for free vibrations of rectangular thin plates. International Journal of Mechanical Sciences, Vol. 140, 2020, p. 455-470.
-
Tang D., Pang F., Li L., Yao X. A semi-analytical solution for in-plane free waves analysis of rectangular thin plates with general elastic support boundary conditions, International Journal of Mechanical Sciences, Vol. 168, 2020, p. 105290.
-
Bao S., Wang S. A generalized solution procedure for in-plane free vibration of rectangular plates and annular sectorial plates. Royal Society Open Science, Vol. 4, 2017, p. 170484.
-
Tufoi M., Gillich G. R., Praisach Z. I., Ntakpe J. L., Hatiegan C. An analysis of the dynamic behavior of circular plates from a damage detection perspective. Romanian Journal of Acoustics and Vibration, Vol. 11, Issue 1, 2014, p. 41-46.
-
Wang G., Wereley N. M. Free in plane vibration of rectangular plates. AIAA Journal, Vol. 40, Issue 5, 2012, p. 953-959.
-
Singh A. V., Muhammad T. Free in plane vibration of isotropic non-rectangular plates. Journal of Sound and Vibration, Vol. 273, Issues 1-2, 2004, p. 219-231.
-
Adrianov I. V., Awrejcewicz J., Chernetskiy V. Analysis of natural in plane vibration of rectangular plates using homotopy perturbation approach. Mathematical Problems in Engineering, Vol. 2006, 2006, p. 020598.
-
Boscolo M., Banerjee J. R. Dynamic stiffness method for exact inplane vibration analysis of plates and plate assemblies. Journal of Sound and Vibration, Vol. 330, 2011, p. 2929-2936.
-
Wu J. L., Liu A. Q., Chen H. L. Exact solutions for free-vibration analysis of rectangular plates using bessel functions. Journal of Applied Mechanics, Vol. 74, Issue 6, 2007, p. 1247-1251.
-
Tufoi M., Gillich G. R., Hatiegan C., Gillich N., Lorenz P. Some aspects regarding the transition from beam to plate behavior of vibrating structures. Romanian Journal of Acoustics and Vibration, Vol. 12, Issue 1, 2016, p. 62-68.
-
Nedelcu D., Gillich G. R. PyPLATE – Python module. Mendeley Data, V1, doi: 10.17632/4d78cwxkg2.1.
