Abstract
The rapid development of aerospace, automobile, national defense and other manufacturing industries has continuously improved the performance requirements of high speed and high positioning accuracy of the CNC machine tool feed system. As the thermal deformation error increases, the system structural rigidity decreases, the vibration increases, and accuracy of machine tool reduces. Existing research mainly focuses on the properties of mechanical and single thermal feed system, and less considers the dynamic performance under the action of thermal-mechanical coupling. For the improvement of feed system performance, it is very beneficiary. This paper takes the high-speed tool of CNC feed system as objective, combined with the actual working conditions to analyze the thermal characteristics, dynamic characteristics and vibration characteristics of the system under the effect of thermal-mechanical coupling. The thermal resistance and convective heat transfer of the key joint surface, the application of moving thermal loads, and the establishment of a simulation model to complete the steady-state temperature field, transient temperature field and thermal-structure coupling analysis. The results show that the maximum temperature rise of the feed system is 21.08 °C, The maximum thermal deformation is 17.264 um. The study found that the parameters such as flow rate and airflow temperature have a significant impact on the cooling effect, so the cooling device was further optimized. This paper proposes a control method for cutting chatter of CNC machine tools based on coupling of characteristics of thermal and mechanical. The thermal characteristic of the feed system and the thermal-mechanical coupling vibration characteristic test provides the maximum temperature error of 3.2 %, verifying the correctness of the theoretical method and analysis model. The highest temperature obtained by the test is 39.7 °C, indicating that the high-speed feed system has a large thermal effect. The relative error of the vibration amplitude of the test and simulation is 12.5 %, which verifies coupling in terms of thermal-mechanical. The accuracy of the vibration analysis method; the experiment depicts that the vibration amplitude increases by 19.7 % under the coupling effect of thermal and mechanical, indicating the effectiveness of dynamic characteristics of the high-speed feed system considering the thermal-mechanical coupling effect.
Highlights
- The maximum temperature rise of the feed system is 21.08℃, The maximum thermal deformation is 17.264um.
- The parameters such as flow rate and airflow temperature have a significant impact on the cooling effect.
- The thermal characteristic of the feed system and the thermal-mechanical coupling vibration characteristic test provides the maximum temperature error of 3.2%.
- The highest temperature obtained by the test is 39.7℃, indicating that the high-speed feed system has a large thermal effect.
1. Introduction
The advancement in information technology has encouraged the modern manufacturing industry to switch to the high-speed machining technology for various applications like aerospace, ship building, automobiles, energy industry, etc [1, 2]. This technology offers the high requirement for CNC machine tools for the improvement in productivity and to reduce the production cost. The factor affecting machining accuracy for high speed CNC machine tools is vibration as it adversely affects work piece quality, its dynamic accuracy, productivity and shortens the service life of the clutters [3, 4]. The stability, precision and efficiency of the CNC machine tools are often dominated by feed drive systems for the static and dynamic performance [5, 6]. Thus, the study of vibration characteristics as well as the corresponding controlling methods for increasing the machining accuracy of the CNC machine tools is of utmost importance. On the contrary, CNC machine tool speed is ensured by high machining precision [7, 8]. These aspects CNC machine tools plays a key role in order to improve the overall accuracy of machine.
With the development of CNC machine tool processing technology, the use of CNC machine tools for cutting processing has become an important part of future mechanical manufacturing. In the process of using CNC machine tools for cutting processing, it is affected by the disturbance factors of shaft parts, resulting in the emergence of CNC machine tools during the cutting process.
The chatter study is equivalent to processes of metal removal and it defined as the self-excited vibration among the different types of vibrations. Chattering, it is necessary to build a CNC machine tool cutting chatter control model, combined with the method of error measurement control, to suppress the CNC machine tool cutting chatter, to improve the CNC machine tool cutting accuracy [9]. The various vibration problems can be avoided by paying attention for process planning stage. The particular sources of vibrations are: cutting tools [10, 11], workpiece material [12, 13] and machine tools [14]. The CNC machine tool cutting control is based on the accuracy control of the measurement system. On the basis, combined with the control of the chattering stability of the CNC machine tool cutting, a linear motor drive method is used to control the chattering of the CNC machine tool cutting to improve the stability of the output.
1.1. Contribution
In the traditional method, the control method of the CNC machine tool chattering chatter PID control method, adaptive zero point control method and follow-up contact measurement method, etc. [15], but the above method is not adaptive enough for CNC machine tool cutting chatter control, and the anti-interference ability is not strong. This work contributes towards the electromechanical coupling characteristics of CNC machine tool cutting chatter control method. Initially, the laser tracking synchronous measurement model of CNC machine tool cutting is constructed, and the method of electromechanical coupling characteristic adjustment is used to perform the follow-up contact measurement during the CNC machine tool cutting process to realize the control of CNC machine tool cutting chatter. Finally, the simulation experiment analysis is carried out, which shows the superior performance of the method in the paper in improving the control of cutting chatter of CNC machine tools [16]. This article contributes in analyzing the thermal, dynamic and thermal-mechanical vibration characteristics of the feed system. The overall performance of the system is improved by maintaining all these factors along with the lightweight design criteria forming a design of multi-objective optimization on the basis of thermal-mechanical coupling, outperforming the conventional methods.
1.2. Organization
The rest of this article is arranged as: Section 2 presents the literature review of existing state-of-the-art techniques in this field; the characteristic research is discussed in Section 3 followed by Section 4 detailing the results and analysis part along with the detailed discussion of suppression optimization method. Section 5 presents the conclusion and future scope of this research work.
2. Literature review
Review of the current research status of thermal characteristics, dynamic characteristics and thermal-mechanical coupling of feed systems at home and abroad create a better understanding of the existing technical levels and improvement needs for providing the research ideas and theoretical support to development of the subject. Park, et al. proposed a machine abnormality detection system by implementing a hybrid learning mechanism, which is basically a combination of unsupervised learning and non-parametric learning approaches of machine learning. For this purpose, vibration data is used, which very well suited for the detection abnormalities in machines during operation. Additionally, considering various other characteristics of abnormalities among data (such as scarcity and diversity), a new approach is designed to detect abnormal behavior using normal patterns instead of abnormal patterns from machines [17]. Liu [18] discussed the influence of stiffness in nut, coupling, radial, along with the length and speed of screw on table vibration of torsional and axial vibration. The second Lagrangian equation is used to establish freedom of multiple degree for vibration of axial torsional coupled mathematical model which takes various factors into account. The influence of variable lead and variable torsional stiffness on the torsional vibration of the table is analyzed. It is observed from the experimental results provide that the design provides future research and theoretical reference for vibration reduction and optimization of structure [18]. Wang, et al. used PROOE software to build a THREE-DIMENSIONAL model of a five-axis CNC machine tool. Firstly, the model is imported into ANSYS software to analyze the dynamic characteristics of the machine tool. The first six natural frequencies and vibration modes are obtained by modal analysis and harmonic response analysis. The experimental results verify the accuracy of the finite element analysis model. Finally, some Suggestions for optimizing the structure of the machine tool are put forward [19]. The onset of vibrations in the cutting tools was characterized by Arnold, et al. [20] indicating chatter origin for sustained forces to estimate cutting process unlike any other external force. The presence of vibrations in the machine tools was determined by the authors in [20-22] occurring because of chip thickness modulation. The dynamic theories machine vibrations which distinguishes among various chatters types was developed by Tobias, et al. [23] and Polacek, et al. [24]. The chatter emerged as a challenging research topic in the past 3 decades and various research initiatives are taken to combat this problem. The most efficient techniques for the prediction of chatter stability, abnormality detection and control were provided by the authors in [25, 26]. Authors adopted three different strategies to combat the challenge. The first strategy includes adequate selection of two cutting parameters: spindle speed and depth of cut. The second method varies the machining parameters by disrupting the regenerative effect and the third approach alters the machine tool dynamics actively while improving the chatter free available zones. A 1D orthogonal cutting model was developed by Tlusty, et al. [27] by introducing efficient solution considering projecting the cutting forces and the structural dynamics in the direction of the chip thickness. The chatter vibrations are maintained by Marui, et al. [28, 29] in their experimental study concluding the friction forces on the contact flank. A 2D model for chatter prediction was proposed by Keneko, et al. [30] which is based in the tests conducted on a cantilevered piece. In this model, work piece behavior that rotates at certain force is inversely proportional to speed of cutting and directly proportional to the velocity of vibration. The transfer function approach of orientation along with 3D cutting geometry was integrated by Minis, et al. [31] while validating the experimentation for orthogonal cutting. The Fourier series expansion for the determination of Fourier coefficients of the corresponding transfer function was applied [32]. Rao and Shin [33] utilized the multidirectional approach proposed by Budak-Altintas [34] for calculating the chip section between the upright directions. All these approaches complicated the system modelling and resolution, thus there is a need for more precise method to overcome the challenges.
3. Characteristic research
The characteristic research is carried out in this work by initially considering the feed system as the main research object. The schematic diagram of experimental measurement points considered for the feed system are depicted in Fig. 1.
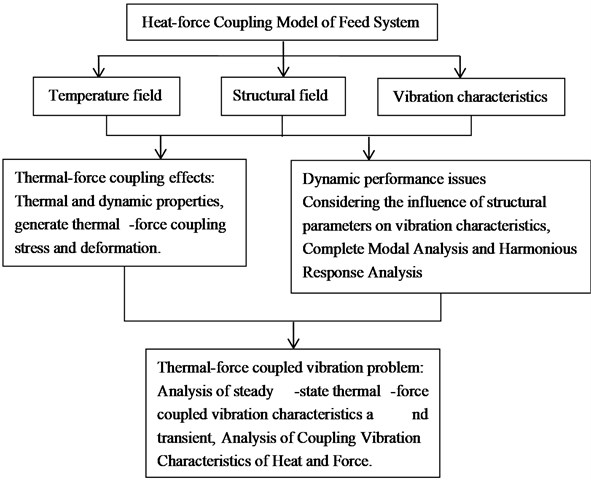
Taking the feed system as the research object, combining the coupling approach of thermal and mechanical, modeling method and analyzing approach, the coupling model of thermal-mechanical feed system is introduced after considering the coupling effect of thermal-mechanical system. It takes into account the thermal-mechanical coupling stress and combines the effects of surface stiffness, system structural stiffness and temperature load [35, 36]. Combined with the simulation model, the analysis process is shown in Fig. 2 to complete the steady-state thermal-mechanical coupled vibration analysis and transient thermal-mechanical coupled vibration analysis for obtaining the impact of coupling effect for thermal-mechanical on dynamic performance.
According to the established thermal-mechanical coupling model, the temperature field, structural field and vibration characteristics are analyzed according to the process depicted in Fig. 2. Set the ball screw speed to 3000 rpm and the ambient temperature to 20 ℃, and obtain the steady-state temperature field according to the thermal characteristic analysis process.
Fig. 1Schematic diagram of experimental measurement points
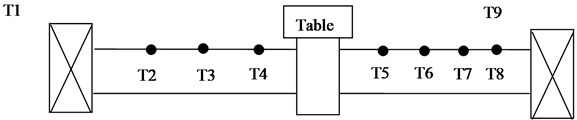
a) Temperature measuring point
b) Thermal deformation measuring point
Fig. 2The overall process of thermal-mechanical coupled vibration analysis of the feed system
4. Results and analysis
The mentioned test conditions and the temperature field outcomes are applied to the structural field in the form of thermal load to obtain the thermal deformation and thermal stress. The thermal-mechanical coupling stress generated by the temperature field and the structural field is used as the prestress, and the joint surface stiffness is considered to be affected by the thermal effect. The temperature load completes the vibration characteristics analysis of the initial stage and thermal equilibrium stage, that is indicated by modal analysis and harmonious response analysis.
4.1. Analysis of temperature field and structure field
The temperature rise occurs at the most severely heated bearing, nut, and other joint surfaces which leads to thermal deformation. The feed system is fixed at both ends, so the thermal deformation of the free part in the middle of the ball screw is the largest, and the transmission accuracy of the system is also higher. The temperature field is loaded into the structural field in the form of thermal load, and the thermal-mechanical coupling stress generated by the thermal stress and the structural stress is used as the prestress to complete the vibration characteristic analysis [37, 38].
4.2. Modal analysis results
Since the rigidity of the fixed joint surface is about 1 to 2 orders of magnitude higher than that of the rolling joint surface, the rolling joint surface is also the key to affecting the dynamic performance. For this vibration characteristic analysis, the rolling joint surface is mainly simplified into a spring-damping unit to represent the stiffness and damping characteristics, the Boolean operation is adopted for the fixed joint surface. Through finite element analysis, the natural frequency and modal vibration mode of the initial state and the thermal equilibrium state are obtained as shown in Table 1.
From Table 1, it is revealed that the natural frequency of the thermal equilibrium state is less than the initial state. The main reason is that the interaction between the temperature field and the structural field will generate thermal-mechanical coupling stress, which will affect the overall stiffness of the system. At the same time, the thermal effect will affect the stiffness of the joint surface, causing the feed system to soften. Especially for the natural frequency and vibration of the low frequency stage, the effect of amplitude is the most obvious, except that the increase of vibration amplitude affects accuracy of feed system in terms of transmission.
Table 1Feed system natural frequency and mode
Order | Initial frequency natural frequency rate Hz | Natural frequency rate after thermal balance Hz | The amount of vibration mode deformation in the initial state mm | The amount of vibration shape deformation after thermal balance mm |
1 | 330.68 | 327.60 | 10.561 | 10.655 |
2 | 354.13 | 350.91 | 10.379 | 10.759 |
3 | 433.41 | 433.33 | 2.7636 | 2.7647 |
4 | 486.83 | 486.81 | 2.8978 | 2.8983 |
5 | 499.67 | 499.62 | 1.7799 | 1.7817 |
6 | 566.16 | 566.01 | 2.7272 | 2.7383 |
4.3. Harmonic response analysis results
Based on the modal analysis, a sinusoidal cutting excitation load is applied to complete the harmonic response analysis [39]. According to the modal analysis, it can be seen that the system is prone to resonance phenomena in the frequency range of 0-800 Hz. Therefore, the harmonic response analysis is performed in the frequency range of 0-800 Hz. The analysis result shows that the vibration is the largest in the frequency range of 300-500 Hz, therefore, the harmonic response analysis is performed in the frequency range of 300-500 Hz to obtain more accurate amplitude curves in the , , and directions.
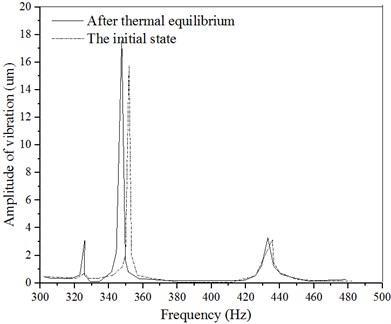
According to the -direction amplitude curve shown in Fig. 3, there are three amplitude peaks in the initial state, the vibration amplitude is 0.64 um, 15.75 um and 3.49 um, and the corresponding frequency is 328 Hz, 352 Hz and 436 Hz. In the thermal equilibrium state, there are three amplitude peaks, which are 3.21 um, 7.58 um and 3.49 um, and the corresponding frequency is 336 Hz, 355 Hz and 436 Hz.
Fig. 3x-direction amplitude curve of the feed system
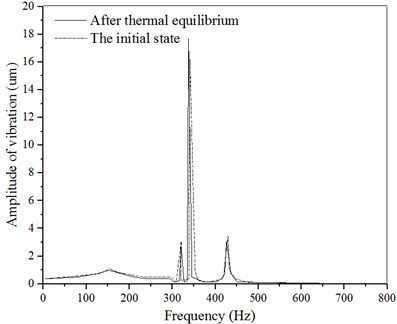
a) 0-800 Hz
b) 300-500 Hz
Fig. 4y-direction amplitude curve of the feed system
a) 0-800 Hz
b) 300-500 Hz
Fig. 5z-direction amplitude curve of the feed system
a) 0-800 Hz
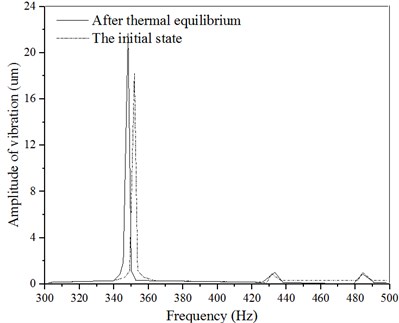
b) 300-500 Hz
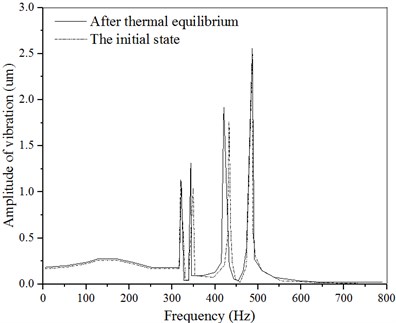
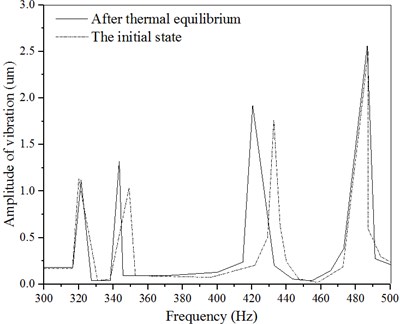
According to the -direction amplitude curve shown in Fig. 4, there are about 4 amplitude peaks in the initial state, which are 0.223 um, 1.09 um, 1.81 um and 2.58 um respectively, corresponding frequencies are 328 Hz, 352 Hz, 432 Hz and 492 Hz. There are also 4 amplitude peaks in the thermal equilibrium state, which are 1.04 um, 1.38 um, 1.96 um and 2.59 um respectively, corresponding frequencies are 336 Hz, 356 Hz, 436 Hz and 494 Hz.
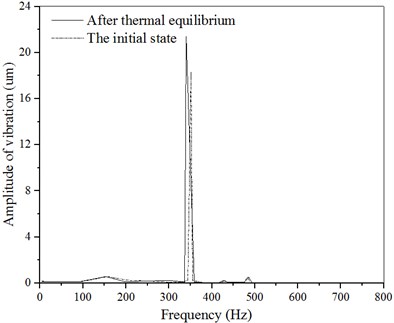
It can be seen from the -direction amplitude curve shown in Fig. 5 that there is an amplitude peak in the initial state, which rises to a peak of 18.6 um at about 352 Hz. There is a peak amplitude at a thermal equilibrium state, which rises to a peak value of 21.58 um at around 354 Hz. From the results of the above simulation analysis, the inferences drawn are as follows:
1) In the low-frequency phase, the vibration amplitude considering coupling effect of thermal and mechanical which is greater than the vibration amplitude without considering coupling effect of thermal and mechanical, and the natural frequency also reduces. In the high-frequency phase, while considering the thermal-mechanical coupling, the vibration amplitude and corresponding frequency change is small.
2) The coupling effect of thermal and mechanical system will change performance of dynamic feed system. The corresponding vibration amplitude of each mode is increased, which intensifies the feed system vibration, and the low frequency phase is most obvious. In the , and directions, the maximum amplitude increased by 11.6 %, 21.0 % and 16.1 % respectively.
3) The temperature rise reduces the feed system frequency and the amplitude of vibration increase. Mainly because the temperature will generate thermal stress, it affects the elastic modulus and other material parameters causing change in feed system’s structural rigidity. At the same time, the combined effect of the field will produce a thermal-mechanical coupling effect which will affect the stiffness characteristics of the rolling joint surface causing the ball screw to “soften”. Especially in the low frequency stage, under the influence of the thermal-mechanical coupling characteristics, the vibration amplitude increases, greatly reducing the system transmission accuracy.
4.4. Suppression optimization method
After studying relationship of coupling among the heated temperature field and the mechanical structure field, a thermal-mechanical coupling modeling method is proposed and simulation analysis is done. From the analysis results, it can be seen that the heat source heat will cause thermal stress, and the coupling effect with the structural field generates thermal-mechanical coupling stress causes the stiffness of the system structure to decrease. In addition, the stiffness characteristics of the joint surface will also be affected by temperature, resulting in a decrease in the dynamic response characteristics of the system and an increase in vibration amplitude. Therefore, reducing heat from the heat source and increasing the stiffness of the system. The following solutions are proposed to improve the accuracy of the system:
4.4.1. Properly increase the rigidity of the joint surface
It can be known from the analysis that the ball screw is the main component that affects the vibration characteristics of the feed system, and the ball screw is also the main transmission component. Therefore, improving the ball screw rigidity is an effective measure to improve the system's vibration resistance. The rigidity of the rolling joint surface is a key link that affects the structural rigidity of the system. To this end, the rigidity of the joint surfaces such as bearings and nuts is appropriately increased for the improvement of system rigidity, thereby achieving improved dynamic response performance.
4.4.2. Add auxiliary support device
In actual processing, the beam supported by the ball screw is heavy, which causes large deformation in the middle part of the screw. For this reason, it is necessary to add a support device in the middle part to reduce the deformation and reduce the transmission accuracy.
4.4.3. Local cooling treatment
From the analysis results of the temperature field, it can be known that the bearing pair and the nut pair are the highest temperature parts, and the thermal deformation error has the largest impact on the transmission accuracy and stability. For this reason, the heat source is cooled by using lubricating oil or coolant, etc. For reducing heat generation, thermal effect reduction on the rigidity of the structure and improve the stability of the system.
4.5. Optimization examples
According to the above analysis, reducing the heat of the heat source and improving the system rigidity are the keys to improving the machining accuracy. For this reason, the cooling device and the method of increasing the rigidity of the joint surface are used to solve the overall performance degradation of the system due to the coupling effect of thermal load and cutting load. This optimization resulted in reducing the feed system structure, the thermal deformation error is reduced, and the feed system vibration also reduced to some extent.
The feed system has an initial ambient temperature of 20 °C at a feed speed of 3000 rpm, uses a cooling device, and preloads the joint surfaces such as bearings and nuts to improve the dynamic performance of the feed system. According to the above-mentioned thermal-mechanical coupling vibration Characteristic analysis process to obtain the temperature field, thermal deformation, natural frequency and feed system amplitude of vibration after adopting these measures.
Comparing the temperature field and thermal deformation before and after optimization, it can be seen from the results of the temperature field that the temperature rise of the feed system is greatly reduced and the temperature field distribution is more uniform by using cooling devices and increasing the rigidity of the joint surface. The results show that the thermal deformation of the ball screw is greatly reduced, mainly because after using the cooling device, the temperature rise of each part decreases and the thermal deformation error decreases; at the same time, the rigidity of the ball screw increases, reducing the deformation caused by temperature rise and gravity.
Comparing the vibration amplitude of the feed system after using the cooling device and increasing the rigidity of the joint surface as shown in Fig. 6, the vibration amplitude of the feed system is greatly reduced after using the kinetic energy performance optimization method. The amplitude in the , , and directions has decreased by 17.8 %, 7.9 % and 18.6 % respectively, because the cooling device is used to reduce the temperature of the feed system. The influence of the temperature system rigidity is also reduced along with the improvement in the system stability and the ball screw rigidity. Especially the rolling joint surface rigidity can be greatly improved, thereby improving the dynamic response performance.
It can be seen from the above analysis that the use of a cooling device and a method of improving the rigidity of the joint surface can not only reduce the temperature of the feed system and the thermal deformation error, but also greatly reduce the vibration amplitude of the system while improving the dynamic response characteristics of the feed system. For this purpose, structural optimization design is performed based on the analysis results to improve the overall performance of the feed system.
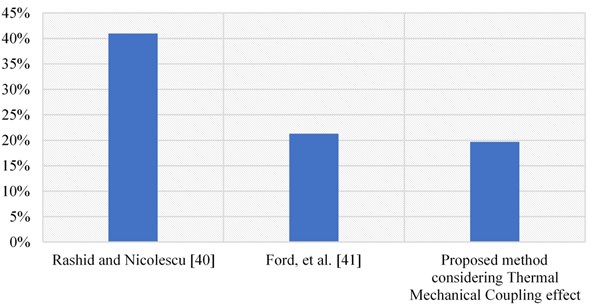
The comparison of the proposed method considering the coupling effect of thermal and mechanical with the other state of the art approaches is provided in Fig. 7.
From Fig. 7, it is revealed that the proposed approach is successful in suppressing the vibrations by incorporating the thermal mechanical coupling, thereby providing the minimum vibration amplitude increased when compared with the other state of the art approaches.
Fig. 6Amplitude curve of the feed system
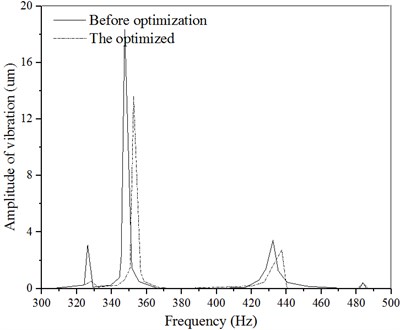
a) direction
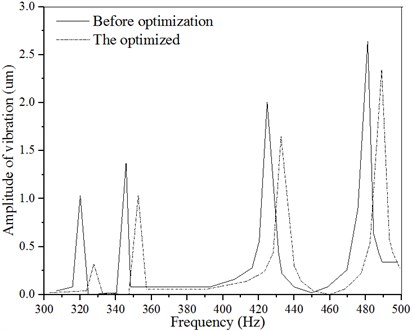
b) direction
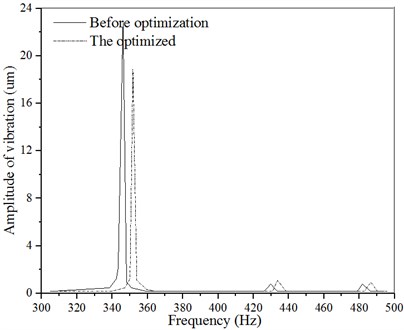
c) direction
Fig. 7Comparison of percentage increase in vibration characteristics
In this paper, the thermal characteristics, dynamic characteristics and thermal-mechanical characteristics of vibration are studied in detail. Through the thermal characteristics study, the influencing factors of the temperature rise and feed system thermal deformation are obtained through the knowledge of dynamic characteristics. Feed system vibration characteristics are attained and the influencing factors of the natural frequency and feed system amplitude are obtained through studying the characteristics of thermal-mechanical coupling. In order to improve the overall performance of the feed system, the thermal performance, dynamic performance and thermal-mechanical coupling vibration performance, combined with lightweight design criteria, forms a multi-objective optimization design method based on thermal-mechanical coupling, thereby tending each index to the best value.
5. Conclusions
Based on the characteristics of the combined effect of thermal load and cutting load on the feed system of high-speed CNC machine tools, this paper explores thermal-mechanical coupled method of feed system vibration, taking into account the thermal performance, mechanical performance and dynamic performance under the coupling of thermal-mechanical performance. The actual working conditions analyze the thermal characteristics, dynamic characteristics and vibration characteristics of the thermal-mechanical coupling to provide a theoretical basis for improving the overall performance of the feed system. In order to ensure the stability of the feed system transmission, the cutting excitation force is calculated and the bearing pair is established. The coupling model of the nut pair and the guide pair calculates the equivalent dynamic parameters of the coupling surface, and combine the feed system analysis model to complete the dynamic modal analysis and harmonious response analysis. The analysis results show that the first-order natural frequency is 330.68 Hz. The speed of the system is far below the critical speed, and no resonance phenomenon will occur; the maximum amplitude in the frequency range of 300-500 Hz is 18.6 um, which meets machine tool requirements.
Feed system thermal characteristics and the thermal-mechanical coupling vibration characteristics test were completed. Compared with the simulation results, the maximum relative error of the temperature was 3.2 %, which verified the correctness of the theoretical method and analytical model provides the maximum temperature measured by the test was 39.7 ℃, indicating that the thermal effect generated by the high-speed feed system is very large. The relative error of the vibration amplitude of the test and simulation is 12.5 %, which verifies the correctness of the thermal-mechanical coupled vibration analysis method. The test measures the vibration under the thermal-mechanical coupling effect and the amplitude is increases by 19.7 %, indicating that the study of the dynamic characteristics of the high-speed feed system needs to consider the thermal-mechanical coupling effect.
The future perspective of this study will focus on competing the other structural optimization techniques. The more in-depth investigation and analysis of the multi-objective optimization design for the feed system is the future scope for this research work.
References
-
King R. Handbook of High-Speed Machining Technology. Springer Science & Business Media, 2013.
-
Schulz H., Moriwaki T. High-speed machining. CIRP Annals, Vol. 41, 1992, p. 637-643.
-
Altintas Y., Verl A., Brecher C., Uriarte L., Pritschow G. Machine tool feed drives. CIRP Annals, Vol. 60, 2011, p. 779-796.
-
Deng C., Yin G., Fang H., Meng Z. Dynamic characteristics optimization for a whole vertical machining center based on the configuration of joint stiffness. International Journal of Advanced Manufacturing Technology, Vol. 76, 2015, p. 1225-1242.
-
Zhang J., Zhang H., Du C., Zhao W. Research on the dynamics of ball screw feed system with high acceleration. International Journal of Machine Tools and Manufacture, Vol. 111, 2015, p. 9-16.
-
Ansoategui I., Campa F. J. Mechatronics of a ball screw drive using an N degrees of freedom dynamic model. International Journal of Advanced Manufacturing Technology, Vol. 93, 2017, p. 1307-1318.
-
Altintas Y., Erkorkmaz K., Zhu W. H. Slidingmode controller design for high speed feed drives. CIRP Annals. Manufacturing Technology, Vol. 49, 2000, p. 265-270.
-
Altintas Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design. Cambridge University Press, 2012.
-
Yao Xiwen, Zhou Haodong, et al. Systematic study on ash transformation behaviour and thermal kinetic characteristics during co-firing of biomass with high ratios of bituminous coal. Renewable Energy, Vol. 147, 2020, p. 1453-1468.
-
Astakhov V. P., Davim J. P. Tools (Geometry and Material) and Tool Wear. Springer, London, 2008, p. 29-57.
-
Astakhov V. P., Outeiro J. C. Metal Cutting Mechanics, Finite Element Modelling. Springer, London, 2008, p. 1-27.
-
Rech J., Hamdi H., Valette S. Workpiece Surface Integrity. Springer, London, 2008, p. 59-96.
-
Asthakov V. P., Davim J. P. Machining of Hard Materials. Springer, Berlin/Heidelberg, Germany, 2008, p. 97-126.
-
Lopez De Lacalle, Lamikiz L. N. A Machine Tools for High Performance Machining. Springer, Berlin/Heidelberg, Germany, 2009.
-
Liu J., Wang Y., Kanungo D. P., Wei J., Bai Y., Li D., et al. Study on the brittleness characteristics of sand reinforced with polypropylene fiber and polyurethane organic polymer. Fibers and Polymers, Vol. 20, Issue 3, 2019, p. 620-632.
-
Zhang Y., Zhang Y., Li Y., Li Q., Zhang J., Yang C. Study on the characteristics of coal spontaneous combustion during the development and decaying processes. Process Safety and Environmental Protection, Vol. 138, 2020, p. 9-17.
-
Park S., Kang J., Kim J., Lee S., Sohn M. Unsupervised and non-parametric learning-based anomaly detection system using vibration sensor data. Multimedia Tools and Applications, Vol. 78, Issue 4, 2019, p. 4417-4435.
-
Liu N. Quantitative analysis for effects of structural stiffness on vibration characteristics of machine tool feed system. Journal of Vibroengineering, Vol. 22, Issue 2, 2020, p. 241-251.
-
Wang S., Wang H., Han Q., Gao Y., Ge L. Analysis of dynamic characteristics of five-axis cnc machine tool. The Journal of Engineering, Vol. 23, 2019, p. 8790.
-
Arnold R. Cutting tools research: report of subcommittee on carbide tools: the mechanism of tool vibration in the cutting of steel. Proceedings of the Institution of Mechanical Engineers, Vol. 154, Issue 1, 1946, p. 261-284.
-
Rathee G., Sharma A., Kumar R., Iqbal R. A secure communicating things network framework for industrial IoT using blockchain technology. Ad Hoc Networks, Vol. 94, 2019, p. 101933.
-
Tlusty J., Polacek M. The stability of machine tools against self-excited vibrations in machining, Proceedings of the ASME International Research in Production Engineering, Pittsburgh, USA, 1963, p. 465-474.
-
Tobias S. A. Machine tool vibration research. International Journal of Machine Tool Design and Research, Vol. 1, Issues 1-2, 1961, p. 1-14.
-
Merritt H. E. Theory of self-excited machine-tool chatter: Contribution to machine-tool chatter research – 1. Journal of Engineering for Industry, Vol. 87, Issue 4, 1965, p. 447-454.
-
Siddhpura M., Paurobally R. A review of chatter vibration research in turning. International Journal of Machine Tools and Manufacture, Vol. 61, 2012, p. 27-47.
-
Kashyzadeh K. R., Ostad Ahmad Ghorabi M.-J. Study of chatter analysis in turning tool and control methods – a review. International Journal of Emerging Technology and Advanced Engineering, Vol. 2, Issue 4, 2012, p. 1-5.
-
Tlusty J. Dynamics of high-speed milling. Journal of Engineering for Industry, Vol. 108, Issue 2, 1986, p. 59-67.
-
Marui E., Ema S., Kato S. Chatter vibration of lathe tools. Part 1: General characteristics of chatter vibration. Journal of Engineering for Industry, Vol. 105, Issue 2, 1983, p. 100-106.
-
Marui E., Ema S., Kato S. Chatter vibration of lathe tools. Part 2: On the mechanism of exciting energy supply. Journal of Engineering for Industry, Vol. 105, Issue 2, 1983, p. 107-113.
-
Kaneko T., Sato H., Tani Y., Hori O.-M. Self-excited chatter and its marks in turning. Journal of Engineering for Industry, Vol. 106, Issue 3, 1984, p. 222-228.
-
Minis I. E., Magrab E. B., Pandelidis I. O. Improved methods for the prediction of chatter in turning, part 3: a generalized linear theory. Journal of Engineering for Industry, Vol. 112, Issue 1, 1990, p. 28-35.
-
Minis I., Yanushevsky R. A new theoretical approach for the prediction of machine tool chatter in milling. Journal of Engineering for Industry, Vol. 115, Issue 1, 1993, p. 1-8.
-
Rao B. C., Shin Y. C. A comprehensive dynamic cutting force model for chatter prediction in turning. International Journal of Machine Tools and Manufacture, Vol. 39, Issue 10, 1999, p. 1631-1654.
-
Budak E., Altintas Y. Analytical prediction of chatter stability in milling – part I: general formulation. Journal of Dynamic Systems, Measurement, and Control, Vol. 120, Issue 1, 1998, p. 22-30.
-
Fang P., Gong Z., Wang Z., Wang Z., Meng F. Study on combustion and emission characteristics of microalgae and its extraction residue with tg-ms. Renewable Energy, Vol. 140, 2019, p. 884-894.
-
Shang Z., Gao D., Jiang Z., Lu Y. Towards less energy intensive heavy-duty machine tools: power consumption characteristics and energy-saving strategies. Energy, Vol. 178, 2019, p. 263-276.
-
Dmytro Fedorynenko, Rei Kirigaya, Yohichi Nakao Dynamic characteristics of spindle with water-lubricated hydrostatic bearings for ultra-precision machine tools. Precision Engineering, Vol. 63, 2020, p. 187-196.
-
Shen J., Xu P., Yu Y. Dynamic characteristics analysis and finite element simulation of steel-bfpc machine tool joint surface. Journal of Manufacturing, Maintenance and Engineering, Vol. 142, Issue 1, 2019, p. 011006.
-
Jun X., Fei L., Wei C. Research on the characteristics and methodology for predicting energy efficiency during the service process of machine tools. Journal of Mechanical Engineering, Vol. 55, Issue 17, 2019, p. 172-184.
-
Rashid A., Nicolescu C. M. Active vibration control in palletised workholding system for milling. International Journal of Machine Tools and Manufacture, Vol. 46, Issues 12-13, 2006, p. 1626-1636.
-
Ford D. G., Myers A., Haase F., Lockwood S., Longstaff A. Active vibration control for a CNC milling machine. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 228, Issue 2, 2014, p. 230-245.
About this article
The authors acknowledge the funding support by the Key Science and Technology Projects of Henan Province (172102210027).
