Abstract
This paper proposes the improved scheme of interaction of containers with the load-bearing structure of the wagon when transporting by rail ferry. In order to ensure the stability of the container balance in the event of fluctuations in the railway ferry, it is proposed to attach special structures to the support structure of the wagons. To reduce the dynamic loading of containers, a material with damping properties is installed on the internal surfaces of the superstructures. Mathematical modelling was performed to substantiate the proposed technical solution. It was found that the total amount of acceleration that acts on the container is 3.47 m/s2 (0.35 g), and on the load-bearing structure of the wagon 2.47 m/s2 (0.25 g), which is 38 % and 23 % less, respectively, for the acceleration values in the typical scheme of their interaction. The conducted research will contribute to improving the efficiency of combined transport through the international transport corridors.
1. Introduction
The development of foreign economic relations between independent countries requires the commissioning of combined transport systems. Such systems have established themselves as a reliable and perspective parts of transport infrastructure.
In fact, the container transportation is one of the most successful and widespread among combined transport systems. To improve the efficiency of this type of transport, container trains are being transported by sea. An example is The New Silk Road transport corridor, which includes two railway and ferry routes across the black and Caspian seas.
Transportation of container trains by sea is accompanied by loads on them that are not inherent in the operating conditions for the tracks. The typical scheme of interaction between the container and the wagon in the conditions of fluctuations of the railway ferry does not provide stability of the balance. This situation may contribute to the violation of combined transport traffic safety. Therefore, there is a need to improve the scheme of interaction between containers and load-bearing structures of wagons during transporting on railway ferries.
Determination of the dynamic loading of a wagon with containers is made in [1]. This model is proposed that allows taking into account the movement of the container at the longitudinal loading of the wagons. Results of studying the dynamics of the wagon under operational loading conditions using multi-body methods are given in [2]. The calculation was made for a centre pin wagon in the MSC Adams software environment. At the same time, these works do not pay attention to the study of the dynamics of rolling stock during transportation on a railway ferry.
Structural features of the new-generation wagon are discussed in [3]. The main requirements for the organization of combined transport technology are specified. Prospects for the operation of combined transport in international traffic are presented. The calculation of the dynamics of a railway wagons with an open loading platform is carried out in [4]. In this case, the study of stability against overturning of the wagons was done when it was inscribed in a curve with a radius of 250 m, taking into account different speeds. It is important to note that the issues of dynamic loading of load-bearing structures of wagons during transportation on railway ferries are not covered in the considered works.
The study of dynamic loading of containers during transportation as part of combined trains on railway ferries is carried out in [5, 6]. The permissible tilt angles of the railway ferry are determined, which ensure the stability of the containers relative to the frame of the wagons. However, measures to improve the load-bearing structures of wagons in order to ensure the stability of the balance of containers are not covered in these works. A comprehensive definition of the strength of an articulated wagon for transporting heavy-load containers is given in [7]. At the same time, the research was carried out on a prototype wagons. The results of the research confirmed the reasonableness of the decisions made. Features of calculating the strength of the load-bearing structure of a new-generation wagon are given in [8]. The wagons have a swivel frame for transporting containers and loading and unloading them according to the ACTS system. However, the study of the dynamics and strength of the load-bearing structure of the wagon containers during transportation on a railway ferry in these works is not paid attention.
It should be noted that measures to reduce the dynamic loading of platform wagons with containers during transport on rail ferries have not yet been properly initiated. Therefore, the research presented in this article is relevant and has a scientific novelty.
2. Creating the computational model
The research conducted by the authors of the article [9] has established that the typical scheme of interaction between the wagon and the container does not ensure the stability of the container during sea transportation. In this regard, it is advisable to use wagons of model 13-9744 (TU 3182-002-47766175-2004) with special superstructures for transporting containers as part of combined trains. It is also possible to install such removable superstructures on the supporting structures of other models of wagons that are used for railway and ferry transport.
As a part of this study, the model 13-401 wagon was selected as a prototype. The load-bearing structure of the wagons, taking into account the installation of removable superstructures, is shown in Fig. 1.
Fig. 1Improved load-bearing structure of the wagons a) in an empty state, b) in a loaded state
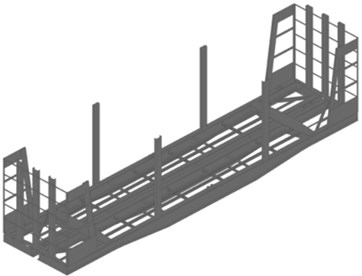
a)
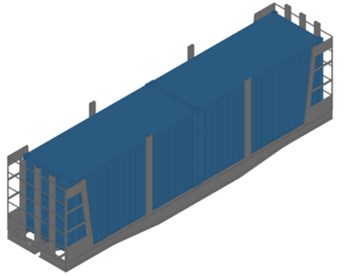
b)
To reduce the dynamic loading of containers, it is proposed to install a material with viscous properties on the internal surfaces of superstructures. Mathematical modelling was performed to substantiate the proposed solution. The calculation scheme is shown in Fig. 2. At the same time, it is considering that fixing the wagons relative to the deck of the railway ferry is carried out according to a standard scheme. This means that four mechanical stop-jacks are used to de-load the spring suspension of the wagons, which are installed under the pin beams of the frame. Eight chain ties are also used, which are attached at one end to the supporting structure of the wagons, and the other to the deck eye. Under the extreme wagons in the couplings, brake shoes are installed. Also, the extreme wagons in the couplings interact with dead-end stops.
Fig. 2Diagram of a wagon with container
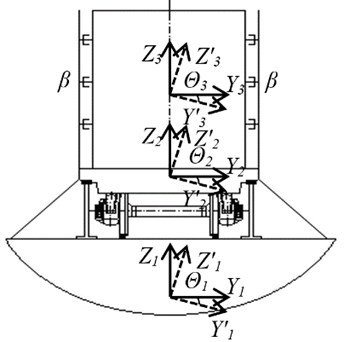
The mathematical model of the movement of the wagon during viscous interaction with containers has the following form:
where – generalized coordinate that corresponds to the angular movement around the longitudinal axis of a railway ferry, – generalized coordinate, which corresponds to the angular movement around the longitudinal axis of the wagons, – generalized coordinate that corresponds to the angular movement around the longitudinal axis of the container.
2.1. For a railway ferry
– the weight displacement, – width, – depth, – coefficient of resistance to vibrations, – coordinate of the centre of gravity, – wind load on the surface projection, – the law of action force which causes the motion of the train ferry with cars placed on the decks.
2.2. For wagon containers
– moment of inertia of the wagons, – height of the side surface of the wagons, – wind load on the side surface of the wagons – the moment of forces that occurs between the wagon the deck of a railway ferry when angular movements relative to the longitudinal axis, – the moment of forces that occurs between the wagon containers during angular movements relative to the longitudinal axis, – force moment of container, – height of the side surface of the container, – wind load on the side surface of the container, – the moment of forces that occurs between the container and the wagon during angular movements relative to the longitudinal axis, – the coefficient of viscous resistance between the load-bearing structure of the wagon the container.
Determination of the coefficient of resistance to vibrations of a railway ferry was carried out according to the method given in [10, 11].
During process of building the model, the impact of sea waves was not taken into account. The motion of the wave was described as a trochoidal law:
where and are the horizontal and vertical coordinates of the centre of the path along which the body that currently has the and coordinates is fighting, is the radius of the path along which the rotation occurs, is the frequency of the sea wave, is the frequency of the wave path. The frequency of the disturbance is determined taking into account the course angle of the wave with respect to the hull of the railway ferry:
where – railway ferry speed, – coefficient, which depends on the shape of the contours of the vessel, – course angle of the wave with respect to the hull:
where – length of the vessel, – angle of the wave relative to the body.
Moments of forces arising between the wagon and the deck, as well as between the wagon and the container, the horizontal components of the gross weight of the wagon the container, respectively, are taken into account. Calculations were made for the railway ferry “Geroy Shypka”, moving in the black sea. The solution of the system of differential Eq. (1) was performed using the Runge-Kutta method [12-21].
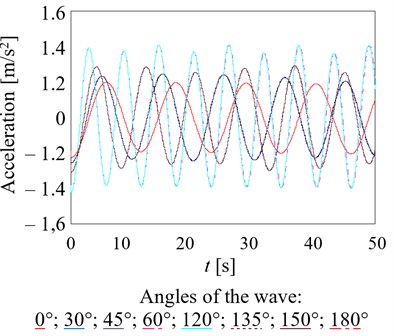
The initial displacements and velocities are assumed to be zero. The coefficient of viscous resistance should not be in the range 0.5-1.2 kNs/m. At the same time, the maximum acceleration of the wagons-platform – 0.4 m/s2 (Fig. 3(a)), of the container was about 1.4 m/s2 (Fig. 3(b)). The numerical values of accelerations are given without taking into account the component of gravitational acceleration.
The total amount of acceleration can be determined:
where – acceleration, which applies to the regular position of the wagon with containers on the deck; – acceleration of free fall; – the roll angle of the rail ferry.
Considering the hydrometeorological characteristics of the Black Sea area and the projection of a surface railway ferry of the “Geroy Shypka”, the obtained value of the roll angle of a railway ferry is 12.2°. The roll value is calculated for the case of static wind action on the surface projection of a railway ferry [10].
Then, the total amount of acceleration that acts on the container is 3.47 m/s2 (0.35 g), a on the load-bearing structure of the wagon – 2.47 m/s2 (0.25 g).
Therefore, taking into account the introduction of a viscous connection between the load-bearing structure of the wagon containers, it becomes possible to reduce the dynamic load, respectively, by 38 % and 23 % compared to the typical interaction scheme.
Fig. 3a) Accelerations acting on the load-bearing structure of the wagons when transporting on a railway ferry b) accelerations applied to the container during transportation on the railway ferry
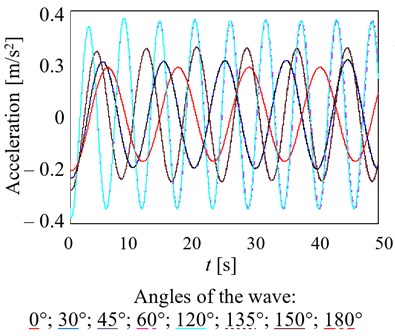
a)
b)
3. Conclusions
The load-bearing structure of the wagon was improved in order to ensure the stability of containers during transportation by rail ferry. It is proposed to install removable superstructures on the supporting structure of the wagons. To reduce the dynamic loading of containers, it is proposed to install a material with damping properties on the internal surfaces of the wagons structures.
Mathematical modelling of the dynamic loading of containers was carried out, considering the new scheme of interaction with the wagons. Based on the calculations was found that the greatest acceleration values occur at the course angles of the wave relative to the hull of the railway ferry. The total acceleration value that acts on the container is 3.47 m/s2 (0.35 g) and on the load-bearing structure of the wagon is 2.47 m/s2 (0.25 g). The viscous connection among the load-bearing structure of the wagon and containers enables to reduce the dynamic load, respectively, by 38 % and 23 % compared to the typical interaction scheme.
The research conducted will help to improve the efficiency of combined transport and can also be useful in developing and creating new car designs.
References
-
Nikitchenko A., Artiukh V., Shevchenko D., Prakash R. Evaluation of interaction between flat car and container at dynamic coupling of flat cars. MATEC Web of Conferences, Vol. 73, 2016, p. 04008.
-
Wójcik K., Malachowski J., Baranowski P., Mazurkiewicz Ł., Krasoń W. Multi-body simulations of railway wagon dynamics. Journal of KONES, Vol. 19, Issue 3, 2012, p. 499-506.
-
Nader M., et al. Rail transport carriage as a novel, innovative design solution for the transport of semi-trailers and road trains for intermodal transport. Logistyka, Vol. 4, 2014, p. 2271-2279, (in Polish).
-
Nader M., Sala M., Korzeb J., Kostrzewski A. Simulations of motion of prototype railway wagon with rotatable loading floor wagonsried out in MSC Adams software. Journal of KONES, Vol. 19, Issue 4, 2015, p. 495-502.
-
Fomin О., Lovska A., Melnychenko O., Shpylovyi I., Masliyev V., Bambura O., Klymenko M. Determination of dynamic load features of tank containers when transported by rail ferry. Eastern-European Journal of Enterprise Technologies, Vol. 5, Issues 7(101), 2019, p. 19-26.
-
Fomin O., Lovska A., Masliyev V., Tsymbaliuk A., Burlutski O. Determining strength indicators for the bearing structure of a covered wagon’s body made from round pipes when transported by a railroad ferry. Eastern-European Journal of Enterprise Technologies, Vol. 1, Issue 7, 2019, p. 33-40.
-
Bubnov V. M., Myamlin S. V., Gurzhi N. L. Experimental studies of an articulated wagon platform car for large containers model 13-1839. Nauka Ta Progres Transportu, Visnik Dnipropetrovskogo Natsionalnogo Universitetu Zaliznichnogo Transportu, Vol. 28, 2009, p. 12-16, (in Russian).
-
Chlus K., Krason W. Dynamic analysis of railway platform chassis model. Journal of KONES, Vol. 18, Issue 2, 2011, p. 93-100.
-
Lovska A. Peculiarities of computer modeling of strength of body bearing construction of gondola wagons during transportation by ferry-bridge. Metallurgical and Mining Industry, Vol. 1, 2015, p. 49-54.
-
Blagoveshchensky S. N., Kholodilin A. N. A Reference Book on the Statics and Dynamics of a Ship. Shipbuilding, Leningrad, 1975, (in Russian).
-
Makov Yu. L. Pumping of Ships. Kaliningrad, KSTU, 2007, (in Russian).
-
Fomin O. V., Burlutsky O. V., Fomina Yu. V. Development and application of cataloging in structural design of freight wagons building. Metallurgical and Mining Industry, Vol. 2, 2015, p. 250-256.
-
Kučera P., Píštěk V. Truck vibrations caused by rotating shaft deflection. Journal of Vibroengineering, Vol. 19, Issue 7, 2017, p. 5361-5373.
-
Píštěk V., Klimeš L., Mauder T., Kučera P. Optimal design of structure in rheological models: an automotive application to dampers with high viscosity silicone fluids. Journal of Vibroengineering, Vol. 19, Issue 6, 2017, p. 4459-4470.
-
Zajac R., Prokop A., Řehák K. Determination of the modal parameters on the thin flat structures. Vibroengineering Procedia, Vol. 18, 2018, p. 91-95.
-
Zajac R., Řehák K., Prokop A. Investigation of the harmonic response on the simple structure in structural and acoustic domain by experimental and numerical approach. Transport Means, 2018, p. 669-672.
-
Tůma J., Kočí P. Calculation of a shock response spectrum. 12th International Carpathian Control Conference (ICCC), Velke Karlovice, Czech Republic, 2011, p. 408-413.
-
Tůma J., Kočí P. Calculation of a shock response spectrum. Colloquium Dynamics of Machines, Prague, Czech Republic, 2009, p. 408-413.
-
Fomin O., Gerlici J., Lovska A., Kravchenko K., Prokopenko P., Fomina A., Hauser V. Durability determination of the bearing structure of an open freight wagon body made from round pipes during its transportation on the railway ferry. Communications-Scientific letters of the University of Zilina, Vol. 21, Issue 1, 2019, p. 28-34.
-
Kiryanov D. V. Mathcad 13. St. BHV, Petersburg, 2006, (in Russian).
-
Drápal L., Šopík, L. Influence of crankshaft counterweights upon engine block load. Proceedings of the 20th International Scientific Conference Transport Means, Lithuania, 2016, p. 809-814.
About this article
The present study was conducted within the framework of the scientific topic of young scientists “Innovative principles of creation of resource-saving structures of railroad cars by taking into account the refined dynamic loads and functional-adaptive flash concepts”, which is funded by the state budget of Ukraine in 2020 and the authors gratefully acknowledge funding from the Specific research on BUT FSI-S-20-6267.
