Abstract
Since the first usage of absorbing structures to modify architectural acoustics the dampening of low frequencies has proven to be a difficult issue. Due to the rise of the population and concentration of said population in urban areas, also known as urban densification, the noise level has risen over the last years. A long-term exposure to noise can lead to serious health problems such as high blood pressure and sleep deprivation. The omnipresent sound in urban areas has a direct impact on the personal well-being. Currently used broadband absorbers work well in a frequency range from 300 Hz to 5 kHz. The dampening of frequencies below 300 Hz, especially below 200 Hz, requires large voluminas due to the wavelength and the absorbing mechanism. To achieve absorption of low frequencies a textile resonator with multiple absorbing mechanisms is proposed. The conversion of energy from the acoustic pressure field in mechanical oscillations as well as heat provides the possibility for efficient absorbers without large voluminas. Compared to common membrane resonators, which similar to Helmholtz resonators use a closed cavity behind the membrane, the textile resonators do not need a closed cavity to generate friction and visco-thermal losses.
1. Introduction
The ongoing urbanization that took place in the last decades led and still leads to a higher density in population and thus leading to more noise pollution due to growth in building construction as well as public and private transport [1]. For example, the population of Munich increased by 1.13 % from 2018 to 2019 [2]. Given the fact that noise can lead to higher stress levels followed by serious health problems, this is an alarming development. A long-time exposure to high noise levels can lead to stress, high blood pressure, insomnia, impairment of cognitive performance in children and other severe diseases [3-6]. About 56 million people in the European Union in areas with more than 250 000 residents are exposed to road noise of more than average 55 dB per year [7]. The urban densification is a health risk for humankind. The solution for this task is the reduction of noise either by reducing the sources or by increasing the effectivity of sound absorption in the relevant environment.
Conventional absorbers work well in a frequency range starting from 200 Hz. This sound absorption can be achieved by using foams, wool or other porous structures. The efficient sound absorption of low frequencies through porous media (< 200 Hz) by visco-thermal dampening requires large volumes, more precise great depth. A porous absorber is most effective when it is positioned at the location of the maximum sound particle velocity in front of a reverberative wall. For example: the lower limiting frequency of 100 Hz requires a depth of /4 hence 85 cm porous structure (in air). The sound transmission loss through a media is given by the mass law:
being the transmission loss, the media mass and the sound wave frequency [8, 9]. The prediction of the mass law states that doubling the mass of the media results in a 6 dB higher transmission loss. Furthermore, it is obvious that lower frequencies require thicker porous media to maintain a given transmission loss. Even the usage of Helmholtz resonators leads to structures with great volume/depth. The resonance frequency of a Helmholtz resonator is defined by the following equation:
where the variable is the resonance frequency, is the speed of sound, the cross section area of the neck, the effective length of the neck and the volume of the cavity [10]. It can be seen that the volume is the key factor in reducing the resonance frequency. In favor of working or living space those high volume structures are generally not considered for the acoustic design.
The presented research focusses on textiles with local resonating structures in order to dampen impinging sound in frequencies lower than 200 Hz. The introduction of a mass on a textile surface, for example an embroidered structure, results in a tunable resonance frequency of such surface. The textile surface itself provides the spring as well as the damper to create a mass-spring-damper system. The impinging sound forces the textile surface to vibrate when the resonance frequency is hit, thus resulting in a rise in the mechanical movement of the textile membrane. The mechanical energy is directly transformed from the incident wave. The movement of the textile was analysed by using laser vibrometry, observing Chladni-sound-figures and FFT-spectrum-analysis of the sound resulting from an impact on the textile surface. In sum, the transformation of sound energy leads to a higher local mechanical energy density which is dampened subsequently by friction in the textile. The performance of the absorber is furthermore increased by visco-thermal effects due to the movement of the textile surface. The movement of the surface provokes an air flow through the pores of the fabric hence leading to friction losses. In summary, the sound energy is reduced by conversion into heat by friction. In conclusion the research in textiles with resonant structures achieved by local resonators allows the manufacturing of thin absorbing panels with a focus on frequencies < 200 Hz. In contrast to currently used low frequency absorbers like Helmholtz or membrane absorbers, the textile resonators have no necessity for a high volume chamber to achieve a significant absorption. A significant health benefit for affected people can be expected.
2. Experimental analysis
To obtain the influences of the textile parameters on the resonance frequencies, a design of experiments based on statistic methods, namely the 2 factorial design, is drafted. Four different parameters (4) are taken into account. The fiber material for all experiments is polyester with a fiber fineness of 167 dtex. The fabric has a grammage of 95 g/m2.
The four parameters are:
– weaving construction (linen or twill);
– mass of the resonator (1 gram or 11 gram);
– width of the area the mass is distributed on (3,8 cm2 and 21,2 cm2);
– fabric stiffness (added metal filaments with 0,3 mm and 0,5 mm diameter to vary the stiffness).
Based on these parameters a set of 16 (24) resonators with three samples of each combination are produced. Fig. 1(a) shows the top view and Fig. 1(b) the bottom view of the textile resonator.
Having established these parameters a roadmap for experiments is generated. Two different analyses are performed.
1) Forming of “Chladni sound figures” by scattering black fine sand onto the surface as resonances of the textile structure are hit (Fig. 2). The experiment is conducted by placing the frame with the textile on a rig with a speaker, and exciting the structure with rising frequencies.
Fig. 1Textile resonator: a) top view and b) bottom view
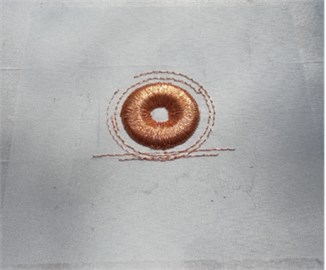
a)

b)
Fig. 2Chladni sound figure on textile resonator

2) FFT-spectrum-analysis of the sound resulting from an impact on the textile surface. Measured with the PULSE-Software and a microphone by Brüel & Kjæer.
Following the determination of the influences, a new designed set of resonators is drafted. Based on the achieved resonator results an improved resonator regarding fibre stiffness, weaving construction and mass is selected for frequencies between 50 and 100 Hz. With this defined resonator the influence of varied forms of frames is tested.
– freely vibrating area of the textile surface (3600 mm2 or 6400 mm2);
– geometry of the frame (square or round).
These four resonators with different frames each are examined for their resonance frequencies with a Polytec PSV-500-3D Scanning Vibrometer.
3. Results
The visual interpretation of the “Chladni sound figures” shows resonance frequencies from 51 Hz to 224 Hz, depending on the structural design.
The FFT-spectrum-analysis determines the first eigenmodes for the textile structures from 38 Hz to 109 Hz. The statistic evaluation of the FFT-spectrum-analysis determines that an added mass on the textile surface has a high impact on a resulting resonance frequency. Adding 10 grams of mass will lower the frequency by 36 Hz. Weaving constructions as well as the fabric stiffness have an effect on the resonance although such effect is significantly lower than the effect of added mass achieved from a set of carried out experiments. The width of the mass distribution is without effect on resonances. In addition to these effects there are reciprocal effects occurring due to the symbiosis between parameters.
The measurements with the laservibrometer showed resonances depending on the different resonator structures. The three following different resonances could be visualized:
– piston-like movement of the added mass; equivalent to the vibration of a speaker membrane;
– tilting of the added mass in two directions of space with two different frequencies;
– oscillations of the textile surface without movement of the mass.
Fig. 3 shows the three different resonances. Blue areas display no movement and red areas indicate a large deflection.
Fig. 3Different resonances of the textile resonator: a) piston-like movement, b) tilting and c) oscillation of the textile surface
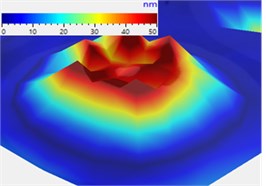
a)
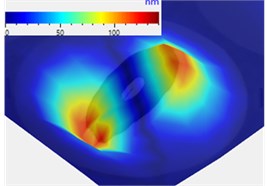
b)
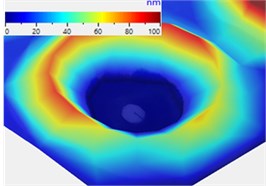
c)
The piston-like movement has a resonance frequency of 72 Hz for the small squares, 65 Hz for the small circles, 30 Hz for the large squares and 39 Hz for the large circles. The amplitude of the small surfaces measured by laservibometry, is lower than 10 nm whereas the amplitude for the larger surfaces is significantly higher than 40 nm.
The tilting happens in two distinct directions in space. These two directions are always orthogonally oriented to each other and vary approximately 10 Hz. Regardless of the direction the amplitudes are in a range from 25 nm up to more than 100 nm. The tilting on the small areas occurs between 38 and 48 Hz while the tilting on the large areas occurs between 60 and 74 Hz. The geometry of the area seems to have no effect at all.
The large areas show oscillations of the textile surface starting from 95 Hz with significant peaks following up at 143 Hz and 192 Hz. Even more resonances can be observed at higher frequencies. For the smaller areas the first resonance occurs at 143 Hz followed up by 192 Hz and other resonances with higher frequencies. The collective resonance frequency of 143 Hz has an amplitude of 8 nm for both larger textile surfaces and 6 nm for both smaller textile surfaces.
4. Discussion of results
The visual interpretation of resonating frequencies via “Chladni sound figures” is a viable experimental analysis in order to gain a first impression of the change in resonance frequencies due to changes in structure. Added mass by the sand as well as the optical interpretation must be seen as critical and as mentioned before this analysis is only suitable for a first impression.
The FFT-spectrum-analysis has proven the functionality of textile resonators at frequencies below 100 Hz. Furthermore, it can be stated, that by altering the textile configuration a change in resonance is achieved. The results offer the opportunity to tune the textile resonator to a desired frequency. Fig. 4 displays the FFT-spectrum as well as the time signal of an exemplary measurement.
The results from the laservibrometer show that a larger textile area leads to a lower resonance frequency (piston-like). This result is similar to the occurrence of eigenfrequencies depending on the geometry of square plates. The tilting in two different directions could be explained by the weaving construction. Warp and weft are rectangularly oriented with different warp densities thus resulting in different tensions.
The three occurring resonances of the textile surfaces all contribute to airflow through the pores of the textile and thus resulting in visco-thermal losses or in other words leading to an increase in the absorption at the corresponding frequencies.
Fig. 4a) FFT-spectrum and b) time signal of an impact on a textile surface with a local resonator
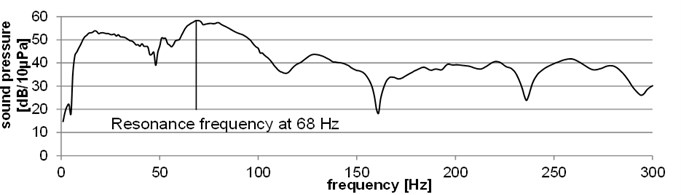
a)
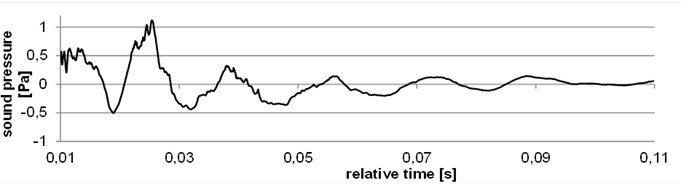
b)
5. Conclusions
The introduction of textile resonators has proven to be successful. The acoustic characteristic of the textile resonators were analyzed by FFT-spectrum-analysis, observing Chladni sound figures and laservibrometry. By altering the textile parameters a change in the resonance frequencies can be achieved. Three different types of resonances occur, whereby these resonances broaden the bandwidth of the absorption capability that already can be achieved with textile resonators. The use of round resonators is a reproductive way of generating the resonators, as the deviation between the resonators of each probe is minimalized with a circular recess below the textile surface.
A first trial of experiments in an impedance tube has shown that a rise of the absorption coefficient for frequencies below 180 Hz is achieved by using the textile resonator compared to a textile surface without added mass. Further trials about the maximization of the effect are planned with a second iteration of changes in the added mass. Changes in the textile structure, for example the use of knitted fabrics, are planned to vary the visco-thermal losses as well as the mechanical properties of the textile resonator. These will further determine the effects of the textile structure on the resonance frequency as well as on the absorption. In additional experiments a closed chamber behind each resonator, with the textile surface being a wall of said chamber, will be examined to directly compare the textile resonators with common membrane resonators. The enclosed air will act as a spring for the moving textile membrane and will be a tuning parameter for the absorbing structure.
References
-
Morillas J., Gozalo G., González D., Moraga P. Noise pollution and urban planning. Current Pollution Reports, Vol. 4, 2018, p. 208-219.
-
Munich, Germany Population 1950-2020. Macrotrends, https://www.macrotrends.net/cities/204371/ munich/population.
-
Daiber A., Herzog J., Münzel T., Schmidt F., Sørensen M., Steven S. Environmental noise and the cardiovascular system. Journal of the American College of Cardiology, Vol. 71, 2018, p. 688-697.
-
Bateni H., Blaschak M., Vaizasatya A. The effect of 80 dB environmental noise on control of posture in healthy young adults. Human Factors and Ergonomics in Manufacturing, Vol. 23, 2013, p. 213-221.
-
Goines L., Hagler L. Noise pollution: A modern plague. The Southern Medical Journal, Vol. 100, 2007, p. 287-294.
-
Stansfels S., Matheson M. Noise Pollution: non-auditory effects in health. British Medical Bulletin, Vol. 68, 2003, p. 243-257.
-
Babisch W. Exposure to environmental noise: risks for health and the environment. Workshop on Sound Level of Motor Vehicles, 2012.
-
Warnock A. Factors affecting sound transmission loss, Canadian Building Digest, CBD - 239, 1985.
-
Ebbitt G., Hansen M. Mass law – calculations and measurements. SAE Technical Paper 2007-01-2201, 2007, https://doi.org/10.4271/2007-01-2201.
-
Greene C., Argo Iv T., Wilson P. A Helmholtz resonator experiment for the Listen Up project. Proceedings of Meetings on Acoustics, Vol. 5, 2008, p. 025001.
About this article
This research would not have been possible without the support and contribution of Robert Mörl from the Polytec GmbH.
This work was supported by the Federal Ministry of Economics and Technology (BMWi) of the Federal Republic of Germany. Funding code: ZF4060056.
