Abstract
The applicational use of structural members in engineering and technology may take the form of a circular plate, for such members it becomes important to predict the vibrational characteristics when operated closer to resonance phenomena. In addition to, the effect of the cutout in the circular plate has a significant effect on modal characteristics. The part of the research work entitled in this paper emphasizes on the modal analysis of a circular plate with clamped boundary condition determined by the characteristics equation and mode shapes of the plate using FEM. The effects of inclusion of cut-out on the vibrational characteristics are discussed. The subject of the analysis was a circular plate considered with certain modifications i.e. free circular plate without cutout clamped on the outer periphery, circular plate with cut-out clamped on the outer periphery, circular plate with cutout clamped on the outer and inner periphery. The methodology applied to conventional material based circular plate is extended to Glass epoxy circular plate with the same set of modifications. The values of natural frequencies for various cases are tabulated and corresponding mode shapes are illustrated.
1. Introduction
An early investigation, along with a comprehensive, detailed survey on free vibration analysis of circular plates was carried out by Leissa [1] and Liew [2]. These researchers mainly used the classical lamination plate theory and first-order shear deformation theories. These theories neglected the effect of rotary inertia and transverse shear deformation, which led to an overestimation of vibrational frequencies. The percentage of error tends to increase with the increase of thickness in the plate. Later, with the advancements carried out in, Shear deformation and higher-order theories considered the effects of both rotary inertia and transverse shear deformation into account. The vibration behaviour of Mindlin plates of annular type with a set of nine different boundary condition combinations is experimented over outer and inner edges by Irie et al. [3]. He used Bessel functions as the basis for clamped-free, free-free, simply supported boundary conditions for performing the analysis. Based on the differential quadrature method, Han et al. [4] performed the free vibration analysis of moderately thick isotropic annular plates based on Mindlin plate theory. Using First-order shear deformation theory, Lin et al. [5] found out the free vibration characteristics of laminated circular and annular plates. Using the finite element method as the basis Ritz method based on the theory of elasticity was used by Kang et al. [6], Leissa [7], Liew et al. [8, 9], Zhou et al. [10] for studying the free vibration analysis of circular and annular plates. A Third order shear deformation theory used by Hosseini Hashemi et al. [11]. The free vibration characteristics of thick laminated circular plates with an attached rigid core was carried out by Hosseini Hashemi et al. [12]. The analogy based on First-order shear deformation theory. The findings for implementation of this method is to produce an exact form of closed solutions for circular plates. A modified Mindlin plate theory was used by Senjanovic [13] for determining the free vibration analysis of circular plates. The free vibration characteristics of polar orthotropic circular and annular plates were analyzed by Powmya et al. [14]. He used Chebyshev collocation technique for finding out the vibrational characteristics, and this technique is based on the First order shear deformation theory. Using the three-dimensional finite element method as the base method the free vibration behaviour of thick circular and annular plates was investigated by Liu [15], the three-dimensional analyses of circular and annular plates resting on Pasternak elastic foundation was analyzed by Zhou et al. [16] and Hosseini Hashemi et al. [17]. The free vibration of annular sector plates using finite element method was investigated Houmat [18]. The analysis on the vibration characteristics of thin circular and annular plates with variable thickness using annular finite element method was carried out by Chen et al. [19]. A three noded annular finite elements for computing the natural frequencies of circular annular plates of variable thickness was employed by Liang et al. [20]. The three-dimensional layer-wise-finite element method for computing the natural frequency of thick-laminated circular and annular plates was used by Malekzadeh et al. [21]. Sumit Khare et al. did the numerical analysis for free vibration characteristics of thick circular laminated plates with clamped-free and simply supported boundary conditions applied at outer edges [22].
2. Finite element analysis technique using CAE
Ansys used as a general-purpose fea tool having a group of engineering simulation programmes with the capability of modelling the structures subject to various loading conditions. Depending on the nature of the problem, it may vary from simple to complicated ones. Both for linear and non-linear it has an extensive library of elements for modelling any geometry. To obtain a high degree of accuracy load adjustments, convergence tolerances are done automatically while carrying out the simulation. The application field of Ansys not only restricted to structural but can be applied to fracture mechanics coupled thermo-electrical field analysis, soil mechanics, static analysis, piezoelectric analysis heat transfer, and acoustics. In this part of research work using Ansys FEA tool as the basis the prediction of modes, natural frequencies of a circular plate with various cutouts is carried out for clamped free conditions. The inputs for the simulation work are boundary conditions, materials, model, and cutout types of geometry.
Table 1MS rectangular plate properties
Properties | Values |
Elastic modulus () | 200 GPa |
Poisson’s ratio () | 0.32 |
Density () | 7850 kg/m3 |
Table 2Composite rectangular plate properties
Properties | Values |
Longitudinal modulus () | 39 GPa |
Transverse modulus () | 8.6 GPa |
Inplane shear modulus () | 3.8 GPa |
Major Poisson’s ratio () | 0.28 |
Minor Poisson’s ratio () | 0.06 |
Density () | 2100 kg/m3 |
Fig. 1Circular plate with a circular cutout

Table 3Dimensions of circular plate with cutouts
Type of plate | Dimensions (mm) |
Circular type | Diameter = 500 |
Type of cutout | Dimensions (mm) |
Circular | 75 |
Rectangular | 100×50 |
Square | 100×100 |
Elliptical | 100×100 |
Triangular | 100×100 |
3. Material and dimensional properties for circular plate with various cutouts
The specimen of a circular plate made of mild steel and glass epoxy material is used for present analysis with the following material properties are plotted in the Table 1, Table 2. The structure is axi-symmetric and formed of isotropic and orthotropic material. Three-dimensional parameters of outer diameter, cutout dimensions, and thickness of the plate are choosen respectively and tabulated in Table 3. Varying cutouts positioned centrally for the circular plate are choosen for the test. The boundary conditions for the plate specimen are inner edge fixed, outer edge fixed and inner-outer edge fixed. The FEA analysis is done on the Ansys software, and the following results are tabulated, and corresponding graphs are plotted.
4. Results and observations
Based on FEM analysis performed by using the numerical software Ansys the free vibration characteristics of circular plates with clamped boundary conditions but having varying cutout shapes and experimented with two different sets of materials one being isotropic and the other orthotropic, the following results are predicted.
4.1. Case1: circular plates with outer edge fixed
From the results plotted in Table 4 in the absence of cutout Fig. 2 and with outer edge fixed for all degrees of freedom isotropic material based circular plate achieved higher operating frequencies than the composite one. With the inclusion of cutout and with varying cutout types for outer edge fixed Fig. 3, it makes clear that the elliptical type cutout achieved higher operating frequencies over all other cutout types both for isotropic and composite materials.
Fig. 2Circular plate with outer edge fixed

Fig. 3Circular plate with cutout and outer edge fixed
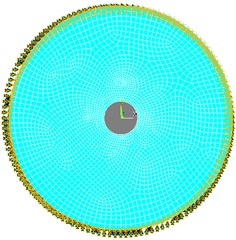
Table 4Circular plate with no cutout
Mode No. | Mild steel | S-Glass epoxy |
1 | 973.43 | 629.59 |
2 | 1975.5 | 1224.8 |
3 | 1976.3 | 1238.1 |
4 | 3153.3 | 1898.8 |
5 | 3154.5 | 1935.0 |
6 | 3575.8 | 2191.1 |
Table 5Circular plate with rectangular cutout
Mode No. | Outer periphery clamped | Outer inner periphery clamped | ||
Mild steel | S-Glass epoxy | Mild steel | S-Glass epoxy | |
1 | 961.38 | 632.01 | 2794.6 | 1694.4 |
2 | 1864.5 | 1154.3 | 2808.2 | 1698.6 |
3 | 1933.8 | 1199.8 | 3115.7 | 1872.3 |
4 | 3068.5 | 1857.0 | 3522.2 | 2102.2 |
5 | 3084.4 | 1864.4 | 3524.4 | 2115.4 |
6 | 3594.3 | 2215.7 | 4557.4 | 2700.5 |
4.2. Case 2: circular plates with inner-outer edge fixed
From the results plotted in Table 5 to Table 9 and with Inner-Outer edge Figs. 4, 5 fixed for all degrees of freedom elliptical type cutout achieved higher operating frequencies over all other cutout types both for isotropic and composite materials followed by the square type cutout.
Fig. 4Circular plate with rectangular cutout and inner and outer edges fixed

Fig. 5Circular plate with square cutout and inner and outer edges fixed
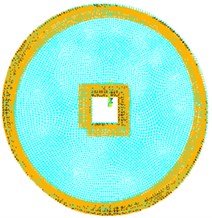
Table 6Circular plate with square cutout
Mode No. | Outer periphery clamped | Outer inner periphery clamped | ||
Mild steel | S-Glass epoxy | Mild steel | S-Glass epoxy | |
1 | 996.0 | 651.1 | 3287.5 | 1974.1 |
2 | 1817.1 | 1142.1 | 3391.6 | 2036.0 |
3 | 1817.5 | 1146.2 | 3392.0 | 2036.5 |
4 | 3005.6 | 1837.7 | 3732.6 | 2262.5 |
5 | 3031.9 | 1860.2 | 3920.8 | 2314.8 |
6 | 3924.5 | 2383.7 | 4721.0 | 2798.1 |
Table 7Circular plate with circular cutout
Mode No. | Outer periphery clamped | Outer inner periphery clamped | ||
Mild steel | S-Glass epoxy | Mild steel | S-Glass epoxy | |
1 | 971.88 | 636.60 | 2698.1 | 1649.6 |
2 | 1932.8 | 1194.5 | 2819.6 | 1706 |
3 | 1933.1 | 1208.8 | 2820.1 | 1721.8 |
4 | 3099.5 | 1888.3 | 3399.6 | 2049.6 |
5 | 3100.5 | 1894.2 | 3400.9 | 2056.6 |
6 | 3647.7 | 2265.2 | 4532.8 | 2706.9 |
Table 8Circular plate with elliptical cutout
Mode No. | Outer periphery clamped | Outer inner periphery clamped | ||
Mild steel | S-Glass epoxy | Mild steel | S-Glass epoxy | |
1 | 1042.6 | 693.17 | 3431.7 | 2078.0 |
2 | 1570.8 | 958.13 | 3438.9 | 2084.0 |
3 | 1904.9 | 1194.8 | 4173.4 | 2478.0 |
4 | 2900.4 | 1757.8 | 4196.9 | 248304 |
5 | 2984.1 | 1822.7 | 4731.7 | 2795.2 |
6 | 4110.1 | 2505.2 | 5083.8 | 2989.5 |
Table 9Circular plate with triangular cutout
Mode No. | Outer periphery clamped | Outer inner periphery clamped | ||
Mild steel | S-Glass epoxy | Mild steel | S-Glass epoxy | |
1 | 954.73 | 628.71 | 2696.9 | 1642.4 |
2 | 1878.3 | 1167.3 | 2841.5 | 1736.0 |
3 | 1895.4 | 1184.5 | 3249.6 | 1946.1 |
4 | 3059.0 | 1860.8 | 3542.1 | 2134.4 |
5 | 3073.1 | 1862.0 | 3674.1 | 2189.9 |
6 | 3538.6 | 2181.0 | 4596.5 | 2721.9 |
4.3. Case 3: circular plates with Inner edge fixed
With the inner edge fixed for all degrees of freedom Figs. 6, 7 and from the results plotted in the Figs. 8-12 and with inner edge fixed and outer edge fixed individually the comparison between the two boundary conditions and materials it reveals that the elliptical type cutout achieved higher operating frequencies over all other cutout types both for isotropic and composite materials followed by the square type cutout.
Fig. 6Circular plate with triangular cutout and inner edge fixed

Fig. 7Circular plate with elliptical cutout and inner edge fixed
Fig. 8Comparison of modal frequencies for circular plate with rectangular cutout having outer fixed and inner periphery fixed
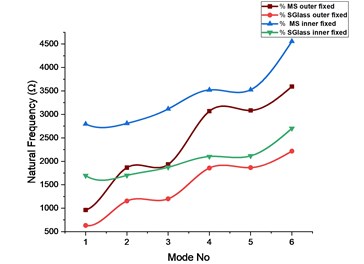
Fig. 9Comparison of modal frequencies for circular plate with square cutout and outer and inner peripheries fixed
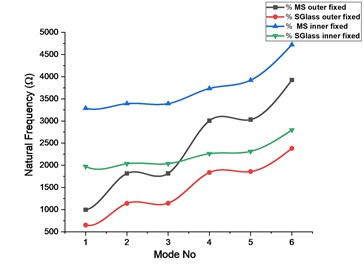
Fig. 10Comparison of modal frequencies for circular plate with circular cutout having outer and inner periphery fixed
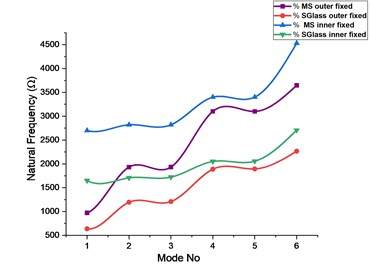
Fig. 11Comparison of modal frequencies for circular plate with circular cutout having outer and inner periphery fixed
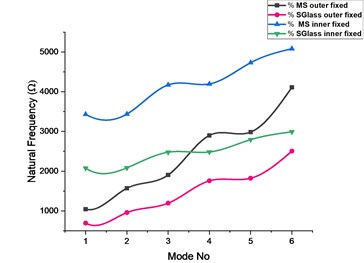
Fig. 12Comparison of modal frequencies of circular plate with outer and inner peripheries fixed
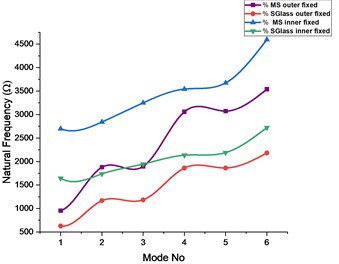
5. Conclusions
The main focus of the work is to understand the free vibrational characteristics behaviour of plates with different conditions of circular blades employed in static working condition. The analysis of circular plates with the determination of vibration characteristics applying with a clamped boundary condition at Outer, Inner, Inner-outer edges having with different cutouts shapes and varying the materials is done with the help of FEM analysis, and corresponding results are predicted. Depending on the various conditions incorporated, the results are concluded in the following fashion.
1) With the replacement of material from isotropic to composite one glass epoxy material, the operating frequencies of isotropic based Mild steel circular plates have higher operating frequencies than composite ones. To achieve better results for composites and cope up with isotropic one’s proper tailoring of ply-stacking sequence, numbers of plies, ply angles are to have experimented.
2) With the incorporation of a cutout in the circular plate positioned centrally, it makes clear that the elliptical type cutout in the circular plate achieved high frequencies of bending, twisting, bending-twisting over all the other cutout types irrespective of the material.
3) The comparison between the edge conditions Outer edge fixed, Inner edge fixed, Inner-Outer edge fixed, applied for the different material based circular plates makes evident that the Inner edge fixed, Inner-Outer edge fixed boundary conditions has superior frequencies than Outer edge fixed ones. By incorporating such boundary conditions over the Outer edge fixed, one’s enhancement in frequencies is achieved.
References
-
Leissa A. W. Vibration of Plates, Office of Technology Utilization. National Aeronautics and Space Administration, Washington, DC, 1969.
-
Liew K. M., Xiang Y., Kitipornchai S. Research on thick plate vibration: a literature survey. Journal of Sound and Vibration, Vol. 180, 1995, p. 163-176.
-
Irie T., Yamada G., Takagi K. Natural frequencies of thick annular plates. Journal of Applied Mechanics, Vol. 49, 1982, p. 633-638.
-
Han J. B., Liew K. M. Axisymmetric free vibration of thick annular plates. International Journal of Mechanical Sciences, Vol. 41, 1999, p. 1089-1109.
-
Lin C. C., Tseng C. S. Free vibration of polar orthotropic laminated circular and annular plates. Journal of Sound and Vibration, Vol. 209, 1998, p. 797-810.
-
Kang J. H., Leissa A. W. Three-dimensional vibrations of thick linearly tapered annular plates. Journal of Sound and Vibration, Vol. 217, 1998, p. 27-944.
-
So J., Leissa A. W. Three-dimensional vibrations of thick circular and annular plates. Journal of Sound and Vibration, Vol. 209, 1998, p. 15-41.
-
Liew K. M., Yang B. Three-dimensional elasticity solutions for free vibrations of circular plates: a polynomials-Ritz analysis. Computer Methods in Applied Mechanics and Engineering, Vol. 175, 1999, p. 189-201.
-
Liew K. M., Yang B. Elasticity solutions for free vibrations of annular plates from three-dimensional analysis. International Journal of Solids and Structures, Vol. 37, 2000, p. 7689-7702.
-
Zhou D., Au F. T. K., Cheung Y. K., Lo S. H. Three-dimensional vibration analysis of circular and annular plates via the Chebyshev-Ritz method. International Journal of Solids and Structures, Vol. 40, 2003, p. 3089-3105.
-
Hosseini-Hashemi S., Es’haghi M., Taher H. R. D., Fadaie M. Exact closed-form frequency equations for thick circular plates using a third-order shear deformation theory. Journal of Sound and Vibration, Vol. 329, 2010, p. 3382-3396.
-
Hosseini-Hashemi S., Rezaee V., Atashipour S. R., Girhammar U. A. Accurate free vibration analysis of thick laminated circular plates with attached rigid core. Journal of Sound and Vibration, Vol. 331, 2012, p. 5581-5596.
-
Senjanovic I., Hadzic N., Vladimir N., Cho D. S. Natural vibrations of thick circular plate based on the modified Mindlin theory. Archives of Mechanics, Vol. 66, 2014, p. 389-409.
-
Powmya A., Narasimhan M. C. Free vibration analysis of axisymmetric laminated composite circular and annular plates using Chebyshev collocation. International Journal of Advanced Structural Engineering, Vol. 7, Issue 2, 2015, p. 129-141.
-
Liu C. F., Lee Y. T. Finite element analysis of three-dimensional vibrations of thick circular and annular plates. Journal of Sound and Vibration, Vol. 233, 2000, p. 63-80.
-
Zhou D., Lo S. H., Au F. T. K., Cheung Y. K. Three-dimensional free vibration of thick circular plates on Pasternak foundation. Journal of Sound and Vibration, Vol. 292, 2006, p. 726-741.
-
Hashemi S. H., Taher H. R. D., Omidi M. 3-D free vibration analysis of annular plates on Pasternak elastic foundation via pRitz method. Journal of Sound and Vibration, Vol. 311, 2008, p. 1114-1140.
-
Houmat A. Three-dimensional hierarchical finite element free vibration analysis of annular sector plates. Journal of Sound and Vibration, Vol. 276, 2004, p. 181-193.
-
Komur M. A., Sen F., Atas A., Arslan N. Buckling analysis of laminated composite plates with an elliptical/circular cutout using FEM. Advances in Engineering Software, Vol. 41, 2010, p. 161-164.
-
Chen D. Y., Ren B. S. Finite element analysis of the lateral vibration of thin annular and circular plates with variable thickness. Journal of Vibration and Acoustics, Vol. 120, 1998, p. 747-752.
-
Liang B., Zhang S. F., Chen D. Y. Natural frequencies of circular annular plates with variable thickness by a new method. International Journal of Pressure Vessels and Piping, Vol. 84, 2007, p. 293-297.
-
Malekzadeh P., Afsari A., Zahedinejad P., Bahadori R. Three dimensional layer wise-finite element free vibration analysis of thick laminated annular plates on elastic foundation. Applied Mathematical Modelling, Vol. 34, 2010, p. 776-790.
-
Yas M. H., Tahouneh V. 3-D free vibration analysis of thick functionally graded annular plates on Pasternak elastic foundation via differential quadrature method (DQM). Acta Mechanica, Vol. 223, 2012, p. 43-62.
-
Tahouneh V., Yas M. H., Tourang H., Kabirian M. Semi analytical solution for three-dimensional vibration of thick continuous grading fiber reinforced (CGFR) annular plates on Pasternak elastic foundations with arbitrary boundary conditions on their circular edges. Meccanica, Vol. 48, 2013, p. 1313-1336.
-
Reddy J. N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. Second ed., CRC Press, Boca Raton, FL, 2004.
-
ANSYS Inc., ANSYS 12.0 Reference Manual, 2009.
