Abstract
Maintaining the leading position of railway transport in the international transportation market led to the creation of its combined interaction with other modes of transport. In countries that have access to international traffic through the sea, rail-ferry services have been developed. At the initial stage of functioning of this symbiosis, only freight and passenger cars were transported by sea. At the moment, it has become possible to follow container trains on railway ferries by sea. An example would be the international Silk Road corridor, which connects Ukraine with China. Important components of this corridor are two rail-ferry routes through the waters of the Black and Caspian Seas.
1. Introduction
To ensure the safety of container trains traveling by sea, it is necessary to determine the dynamic loads acting on them when transported by rail ferries. This will make it possible to formulate recommendations for the safe operation of vehicles during transportation by sea, as well as the creation of their modern designs.
The detailed study of heat flux transfer through the supporting structure of the container is given in [1]. The paper considers the simulation of heat flux through a multilayer resistance made of plastic.
The results of optimization of the supporting structure of the tank container are given in [2]. The work proved the feasibility of designing and putting into operation tank containers as vehicles. An improved design of the tank container for the transportation of light petroleum products has been developed.
Tests of metal and composite containers under the influence of low temperatures are given in [3]. It is determined which types of containers is advisable to use for the transportation of a certain range of goods, taking into account the low ambient temperature. It is important to note that in the considered works no attention is paid to the issues of determining the dynamic loading of containers under operational conditions.
The determination of the dynamic load of a tank container placed on a platform car during shunting collisions is carried out in [4]. Research was conducted by mathematical and computer modelling. When creating models of dynamic load the absence and presence of displacements of fittings relative to fitting stops were taken into account.
The features of calculating the floor strength of a 40-foot container in the Abaqus/CAE version 6.1 software package are given in [5]. Recommendations on the safe operation of this type of container are suggested. The issue of determining the dynamic load of containers during transportation as part of combined trains on railway ferries is not raised in these works.
The determination of the dynamic loading of vehicles during transportation by rail ferries is carried out in [6, 7]. Mathematical models describing the movement of vehicles during transportation by sea are given. However, the issues of determining the dynamic load and stability of tank containers in these works are not covered.
2. Creating of computational model of a tank container placed on a flat wagon
The aim of the research was to study the effect of dynamic loads on the safety of transportation of tank containers as part of combined trains on railway ferries. To achieve this goal, the following tasks have been set:
– to develop a mathematical model for determining the dynamic load of a tank container placed on a platform wagon during transportation by rail ferry.
– to determine the strength of the supporting structure of the tank container placed on the flat wagon when transported by rail ferry.
– to determine the stability coefficient of the tank container placed on a flat wagon during transportation by railroad ferry.
The calculation scheme for researching the dynamic load of a tank container placed on a flat wagon during fluctuations of a railroad ferry is shown in Fig. 1.
Fig. 1Calculating scheme for researching the dynamic load of a tank container placed on a flat wagon during fluctuations of a railroad ferry
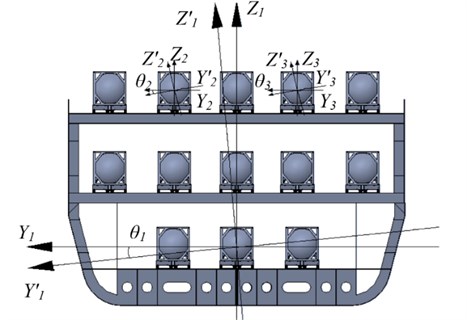
Mathematical model Eqs. (1-3) was developed to determine the dynamic load of the tank container during transportation as a part of intermodal train on the railroad ferry [4, 8]. This model takes into account the movement of the system “railroad ferry – tank container – liquid bulk cargo” at angular movements around the longitudinal axis (Fig. 1). The model assumes that the flat wagon which the tank container is placed rigidly fixed to the deck of the railroad ferry and moves along with it:
where , , are generalized coordinates corresponding to the angular movement around the longitudinal axis, respectively, the railway ferry, the tank container and the liquid bulk cargo. The coordinate system origin is located in the railroad ferry centre of mass.
For tank-container with liquid bulk cargo is the moment of inertia of the pendulum, is the weight of the th pendulum in the th tank container, is the distance from the plane 0 to the point of fixing the th pendulum in the th tank container, is the length of the th pendulum; is the reduced moment of inertia of the th tank container and liquid bulk cargo that does not participate in the movement relative to the boiler, is height of the gravity centre of the tank container; is the mass of the body, which is equivalent to the second tank container with a part of the liquid bulk cargo that does not take part in the movement relative to the boiler, is the force moment between the tank container and the flat wagon.
The description of the process of movements of the tank container with liquid bulk cargo was carried out according to the method shown in [4].
Petroleum is accepted as liquid bulk cargo. Determination of the hydrodynamic characteristics of the liquid bulk cargo was carried out taking into account the maximum permissible loading of the tank container boiler – 95 % of its total capacity in accordance with [9]. The movement of liquid bulk cargo was described by a set of mathematical pendulums [4].
Determination of the coefficient of resistance to the fluctuation of the railroad ferry is carried out according to the method shown in [10].
The impact of sea waves on the hull of a railroad ferry with wagons placed on its board was not taken into account. The trochoidal law of the moving action (of sea wave) on the railroad ferry with wagons located on its decks and the dissipative component that occurs during the fluctuations of the railroad ferry in the conditions of the sea disturbance were taken in account during developing the model, as well as the wave-to-course angle in relation to the railroad ferry hull and the wind load acting on the uncovered projection of the railroad ferry, the flat wagon located on the upper deck and containers.
It is assumed that the container has its own degree of freedom to the time when the vertical wall of the fitting will lean against the fitting.
The research has been conducted relating to the ferry “Geroi Shipki”, which moves along the Black Sea water area. The model 13-4012 was chosen as the basic model of the flat wagon. And the model of 1СС with a gross mass of 24 tons was chosen as a basic model of the container. The hydrometeorological characteristics of the Black Sea area are determined according to the data given in [11].
Differential equations of motion were solved applying the programming environment Mathcad [12-14] by using the Runge-Kutta method.
The results of the studies allowed us to conclude that the maximum accelerations that act on the tank container are about 3.8 m/s². The total acceleration value will be 5.87 m/s2 (0.6 g) taking into account the horizontal component of the acceleration of free fall due to the angle of inclination of the railroad ferry.
The obtained values of the accelerations acting on the tank container when transported on a railway ferry were taken into account when studying the strength of its supporting structure.
The creation of a computer geometric model of the tank container was carried out in the SolidWorks software environment [15]. Strength analysis was performed using the finite element method in the CosmosWorks software environment.
In creating the finite element model of the tank container (Fig. 2(a)), isoparametric tetrahedra were used, the optimum number of which was determined using the graphoanalytical method. The maximum size of the mesh element was 485.68 mm, the minimum – 97.14 mm. The number of grid elements was 169 106, nodes – 56121, the maximum aspect ratio – 68.862, the percentage of elements with an aspect ratio of less than 3 was 6.61, and more than 10-19.3. The construction material of the tank container is 345-09G2S steel.
When creating the computational model, it was taken into account that the vertical-static load , the pressure from the bulk cargo , the dynamic load , as well as the loads in the fittings from the side of the inclination of the tank-container act on the supporting structure of the tank container (Fig. 2(b)). The fastening of the tank container was carried out in the areas of its abutment on a wagon platform.
The calculations showed that the maximum equivalent stresses in the supporting structure of the tank-container are concentrated in the hatch-manhole zone and are about 180 MPa (Fig. 3(a)). Maximum displacements occur in the zone of interaction between the boiler and the backing sheet and are equal to 2.2 mm (Fig. 3(b)). Deformations in the design of the tank container amounted to 0.0013.
Fig. 2Strength calculation of the tank container

a) FE model
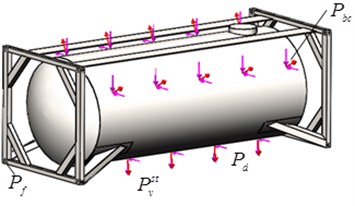
b) Calculation scheme
Fig. 3Strength calculation results of the supporting structure of the tank container
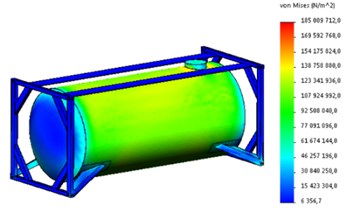
a) Stress state
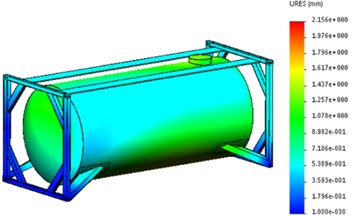
b) Displacements in nodes
That is, when transporting a tank container as part of a combined train on a railway ferry, the strength of its structure is ensured.
In order to determine the critical vibration frequencies of the supporting structure [16, 17] of the tank container with a typical scheme of interaction with the wagon platform, a modal analysis was carried out. The calculated numerical values of the critical vibration frequencies are given in Table 1.
Table 1Critical frequencies of the tank container during transportation as a part of a combined train on a railway ferry
Mode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Frequency [Hz] | 4.82 | 4.95 | 6.31 | 13.52 | 13.67 | 19.56 | 26.01 | 26.67 | 27.8 | 29.16 |
From Table 1 it is seen that the critical oscillation frequencies are outside the acceptable range. This can lead to loss of stability of the tank container relative to the wagon platform and the violation of the stability of the railway ferry.
To ensure the stability of the container's equilibrium with regard to the frame of the flat wagon, the following condition must be fulfilled:
where is the magnitude of the restoring moment, is the magnitude of the overturning moment:
where is the gross mass of the container, is the gross weight of the container, is width of the container, is the number of fitting pieces which support the container at angular movements relative to the longitudinal axis and is height of the fitting piece.
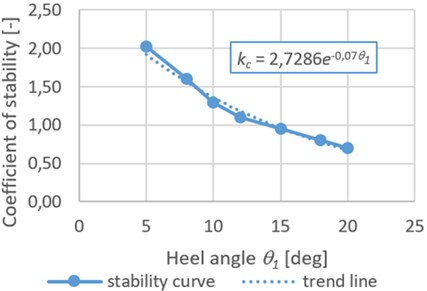
The graphic dependence of the stability coefficient of the tank container relative to the frame of the flat wagon from the heeling angle of the railroad ferry (Fig. 4) was determined on calculations carried out. The stability curve is marked with blue, and the trend line is dotted. The trend line equation is as follows:
It can be seen from Fig. 4 that the stability of the tank container relative to the frame of the flat wagon, taking into account the given calculating scheme, is provided at the heeling angles of the railroad to 12°.
Fig. 4Dependence of the stability coefficient of the tank container placed on a flat wagon on the heeling angle of the railroad ferry
3. Conclusions
The computational model for determining the dynamic load of a tank container placed on a flat wagon during transportation by a railway ferry was developed. The maximum accelerations that act on the tank container are about 3.8 m/s². Taking into account the horizontal component of acceleration of free fall due to the angle of inclination of the railroad ferry, the total acceleration value is 5.87 m/s² (0.6 g). The strength of the supporting structure of the tank container was determined. It has been established that the strength indicators of the tank container are within acceptable limits [18]. Moreover, the maximum equivalent stresses in the supporting structure of the tank container are about 180 MPa, the maximum displacements are 2.2 mm, and the deformations 0.0013. The stability coefficient of the tank container placed on the flat wagon during transportation by a railroad ferry was determined. It was stated that the stability of the tank-container relative to the frame of the flat wagon is provided at the railroad ferry heeling angles up to 12 deg. The conducted studies will contribute to the creation of recommendations for the safe transportation of tank containers on rail ferries by sea, as well as improving the efficiency of combined transport operations.
References
-
Czyżycki W. Modeling of heat flow through multilayer internal supports of cryogenic vessels. Technical Transportations, Vol. 2, 2015, p. 27-34.
-
Myamlin S. V., et al. Promising design of tank containers for transportation of light petroleum products, ammonia and hydrocarbon gases. Zaliznichniy transport Ukrayini, Vol. 2, 2012, p. 44-46, (in Russian).
-
Föhr J., et al. Metal and composite intermodal containers in comparative cold tests with wood chips. Journal of Sustainable Bioenergy Systems, Vol. 5, Issue 1, 2015, p. 32-39.
-
Bogomaz G. I., et al. The Loading of Tank-Containers, Located on the Railway Platform, When Struck in the Coupling. Dynamics and Motion Control of Mechanical Systems, Kyiv, ANU, Institute of Technical Mechanics, 1992, p. 87-95, (in Russian).
-
Rzeczycki A., et al. Strength analysis of shipping container floor with gooseneck tunnel under heavy cargo load. Solid State Phenomena, Vol. 252, 2016, p. 81-90.
-
Fomin O., et al. Research of the strength of the bearing structure of the flat wagon body from round pipes during transportation on the railway ferry. MATEC Web of Conferences, 2018.
-
Fomin O., et al. Determining strength indicators for the bearing structure of a covered wagon’s body made from round pipes when transported by a railroad ferry. Eastern-European Journal of Enterprise Technologies, Vol. 7, Issue 1(97), 2019, p. 33-40.
-
Fomin O., et al. Determination of dynamic load features of tank containers when transported by rail ferry. Eastern-European Journal of Enterprise Technologies, Vol. 5, Issue 7(101), 2019, p. 19-16.
-
Rules for the Transport of Dangerous Goods. to the Agreement on International Railway Freight Traffic. Vol. 3, OSJD, 2011, p. 531, (in Russian).
-
Blagoveshchensky S. N. Reference Guide on Statics and Dynamics of the Ship. Volume 1: Statics of the Ship). Sudostroenie, Leningrad, 1976, p. 176, (in Russian).
-
Wind and Waves in the Oceans and Seas: Reference Data. Transport, 1974, p. 360, (in Russian).
-
Kondratiev A. V., et al. Relationships between the ultimate strengths of polymer composites in static bending, compression, and tension. Mechanics of Composite Materials, Vol. 52, Issue 2, 2019, p. 259-266.
-
Fomin O., et al. Durability determination of the bearing structure of an open freight wagon body made of round pipes during its transportation on the railway ferry. Communications-Scientific letters of the University of Zilina, Vol. 21, Issue 1, 2019, p. 28-34.
-
Fomin O., et al. Determining the dynamic loading on a semi-wagon when fixing it with a viscous coupling to a ferry deck. Eastern-European Journal of Enterprise Technologies, Vol. 2, Issues 7(98), 2019, p. 6-12.
-
Alyamovsky A. A. SolidWorks/COSMOSWorks 2006-2007. Engineering Finite Element Analysis. Moscow, DMK, 2007, p. 784, (in Russian).
-
Zajac R., Prokop A., Řehák K. Determination of the modal parameters on the thin flat structures. Vibroengineering Procedia, Vol. 18, 2018, p. 91-95.
-
Zajac R., Řehák K., Prokop A. Investigation of the harmonic response on the simple structure in structural and acoustic domain by experimental and numerical approach. Transport Means, 2018, p. 669-672.
-
GOST 31232-2004. Containers for the Transport of Dangerous Goods. Operational Safety Requirements. Minsk, 2005, (in Russian).
Cited by
About this article
This work displays the results of international inter-university research and is also an output of the internal BUT research project Reg. No. FSI-S-17-4104.
