Abstract
The article presents result of computational modelling of container dynamic load during transportation as a part of trains of intermodal transport on a railway ferry. The computational models were developed which account the movement of the container with regard to the frame of the flat wagon while moving of the railway ferry. It was assumed that there is no movement of the flat wagon with regard to the deck, since these movements were limited by fastening means. The obtained acceleration rates, as components of the dynamic loads acting on the container, were accounted while determining the containers stability coefficient with regard to the flat wagons. The railway ferry heeling angles which ensure the stability of the containers were determined. The researches will ensure safety of transportation of containers as a part of trains of intermodal transport on a railway ferry, as well as increase the efficiency of operation of intermodal transport in the international transport.
1. Introduction
The development of international economic activity between Eurasian countries enables the commissioning of competitive transport systems. To date the most priority among them is the container transportation. Container transportation as a part of intermodal trains was expanded to reduce the time of cargo delivery and transportation costs. These trains can run not only in relation to main-line railways, but also in international rail and water transportations involving railroad ferries. It is important to study the load of intermodal trains to ensure the safety of their transportation on railroad ferries, as conditions for the container transportation by sea are significantly different from the conditions of their operation relative to the main-line railways. Therefore, the article focuses on the issue of researching the dynamic load of containers during transportation as a part of intermodal trains on railroad ferries and determining the permissible heeling angles at which the stability of containers is ensured in relation to flat wagons.
2. Previous research overview
The peculiarities of using simplified methods for measuring the stress-strain state of the body-container of variable volume are given in [1]. The scheme of load and test methods of body-containers for transverse and longitudinal swash is proposed in the work.
The peculiarities of invention a container for the transportation of fruit and vegetables are covered in [2]. The requirements for the body-container are given, its construction is proposed and the calculation of the strength using the finite element method is made in the article. It is important to note that the study of the dynamic load of containers is not carried out in these works, and the determination of strength indicators is carried out taking into account the regulatory values of loads.
An overview of the structure and properties of nanomaterials obtained by isostatic compression is carried out in [3]. Possibilities of the implementation of this material in bearing structures of vehicles for ensuring strength under operational load conditions is not carried out in the work.
The peculiarities of testing units of rolling stock on roller stand to determine their dynamic properties under operating conditions is carried out in [4]. The work does not specify the possibility of using this equipment to determine the dynamic load of containers during transportation on railroad ferries.
Measures concerning the improvement of the automatic coupling draw gear in order to reduce the dynamic load of wagons are highlighted in [5, 6]. The results obtained by mathematical modelling are confirmed by computer simulation of the dynamic load of wagons.
Identification of the substantiation peculiarities of the open wagon service life prolongation that have exhausted their normative resource is given in [7]. The study of the open wagon dynamic load and strength was carried out taking into account the actual wear values of the bearing structure elements of the open wagon in operation. The task of studying the dynamic load of bearing structures of containers under operating conditions in these works is not stated.
Peculiarities of the improvement of the open wagon bearing structure to ensure the reliability of its fastening on the deck of the railroad ferry are given in [8, 9]. The proposed technical solutions are confirmed by calculations on strength; the results are given in the article. The problems of determining the dynamic loading of containers during transportation as a part of intermodal trains on railroad ferries are not considered in the work.
Other advanced methods for dynamic analysis of mechanical structures, including examples of their application, are described in [10, 11].
3. Computational model of a container placed on a flat wagon
The aim of the research was to create a computational model describing the peculiarities on dynamic load of containers placed on a flat wagon during transportation by a railroad ferry. To achieve this goal, the following tasks were defined:
– to develop a mathematical model for determining the dynamic load of a container placed on a flat wagon during transportation by a railroad ferry;
– to determine the stability coefficient of the container placed on a flat wagon during transportation by railroad ferry.
The calculation scheme for researching the dynamic load of a container placed on a flat wagon during fluctuations of a railroad ferry is shown in Fig. 1.
Fig. 1Calculating scheme for researching the dynamic load of a container placed on a flat wagon during fluctuations of a railroad ferry
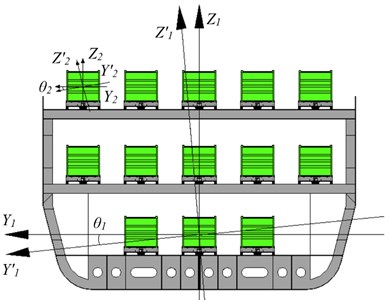
The computational model was developed to determine the dynamic load of the container during transportation as a part of intermodal train on the railroad ferry. This model accounts the angular movements of the elements of the system (“railroad ferry – container”) around the longitudinal axis (roll), as a case of the greatest load of the bearing structure of the container during transportation by railroad ferry, as well as ensuring its stability with respect to the frame of the flat wagon. The model does account the movements of the flat wagon. That is, it is assumed that they are limited by fastening means relative to the deck.
Equations of motion for researching the dynamic load of a container placed on a flat wagon during fluctuations of a railroad ferry [12] can be written in form:
where is a generalized coordinate which corresponds to the angular displacement around the longitudinal axis of a railroad ferry, is a generalized coordinate which corresponds to the angular displacement around the longitudinal axis of the container. The coordinate system origin is located in the railroad ferry centre of mass.
For railroad ferry is the weight displacement, is the width, is the height of the board, is coefficient of resistance to fluctuations, is coordinate of the gravity centre, is the wind load on the uncovered projection, is the time course of force that moves a railroad ferry with wagons located on its decks.
For the container is the moment of inertia of the container, is the height of the side surface of the container, is wind load on the side of the container, is force moment that occurs between the container and the deck at angular movements relative to the longitudinal axis.
Determination of the coefficient of resistance to the fluctuation of the railroad ferry is carried out according to the method shown in [13].
The impact of sea waves on the hull of a railroad ferry with wagons placed on its board was not taken into account. The trochoidal law of the moving action (of sea wave) on the railroad ferry with wagons located on its decks and the dissipative component that occurs during the fluctuations of the railroad ferry in the conditions of the sea disturbance were taken in account during developing the model, as well as the wave-to-course angle in relation to the railroad ferry hull and the wind load acting on the uncovered projection of the railroad ferry, the flat wagon located on the upper deck and containers.
It is assumed that the container has its own degree of freedom to the time when the vertical wall of the fitting will lean against the fitting.
The research has been conducted relating to the ferry “Geroi Shipki”, which moves along the Black Sea water area. The model 13-4012 was chosen as the basic model of the flat wagon and the model of 1СС with a gross mass of 24 tons was chosen as a basic model of the container. The hydrometeorological characteristics of the Black Sea area are determined according to the data given in [14]. The speed of the railroad ferry was assumed to be equal to its operating speed of 18.6 knots (9.57 m/s) and was accounted as permanent when moving along the sea area.
Differential equations of motion were solved applying the programming environment Mathcad [15, 16] by using the Runge-Kutta method.
It was established that the maximum acceleration value acting on the container is about 1.5 m/s² and occurs at the wave-to-course angles of 60 deg and 120 deg in relation to the hull of the railroad ferry. The total value of the acceleration acting on the container is 3.57 m/s² (0.36 g) taking into account the horizontal component of acceleration of free fall, caused by the angle of the railway train ferry. At the same time, the estimated heeling angle of the railroad ferry at a static wind action on the uncovered projection was 12.2 deg.
Studies of the equilibrium stability coefficient were performed at angular movements of the railroad ferry relative to the longitudinal axis in order to assess the stability of containers in relation to the frame of the flat wagon.
The accelerations were taken into account in determining the overturning moment. These accelerations were calculated using mathematical modelling and are the components of the dynamic load acting on the container.
To ensure the stability of the container’s equilibrium with regard to the frame of the flat wagon, the following condition must be fulfilled:
where the magnitude of the restoring moment is the magnitude of the overturning moment are determined by equations:
where is the gross mass of the container, is the gross weight of the container, is the width of the container, is the number of fitting pieces which support the container at angular movements relative to the longitudinal axis and hf is height of the fitting piece.
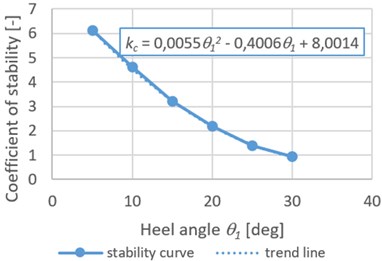
The results of the calculation in the form of characteristic curve are shown in Fig. 2.
In this case, the threshold of stability is established when the magnitudes of the restoring and overturning moments are equal. The stability curve is indicated by blue, the trend line (black colour) is described by the equation:
The conducted studies allowed us to conclude that the stability of the container under this calculation scheme was provided at the corners of the railroad ferry up to 30 deg taking into account the possible movements of container fittings with respect to the fitting of the flat wagon.
Fig. 2Dependence of the stability coefficient of the container placed on a flat wagon on the heeling angle of the railroad ferry
4. Conclusions
The computational model for determining the dynamic load of a container placed on a flat wagon during transportation by a railroad ferry was developed. It was stated that the maximum acceleration value acting on the container is about 1.5 m/s2 and occurs at the wave-to-course angles in relation to the hull of the railroad ferry of 60 deg and 120 deg. The total value of the acceleration acting on the container, taking into account the horizontal component of acceleration of free fall is 3.57 m/s² (0.36 g).
The stability coefficient of the container placed on the flat wagon during transportation by a railroad ferry was determined. Taking into account possible movements of container fittings with respect to fittings of the flat wagon, the container stability is provided at the railroad ferry heeling angle up to 30 deg.
The conducted research will provide the development of recommendations on the safety of container transportation on railroad ferries by sea, clarification of existing regulatory documentation on the design and calculation of vehicles for transportation on railroad ferries [17-19], as well as increase the efficiency of intermodal transport operations.
References
-
Mishuta D. V., et al. Simplified methods for measuring the stress-strain state of a container body of variable volume. Devices and Measurement Methods, Vol. 2, Issue 5, 2012, p. 100-103, (in Russian).
-
Ibrahimov N. N., et al. Development of the design of a container for transportation of fruits and vegetables. Young Scientist, Vol. 21, Issue 101, 2015, p. 168-173, (in Russian).
-
Sirota V. V., et al. Structure and properties of nanoporous ceramic TiO2 obtained by isostatic pressing. Glass and Ceramics, Vol. 69, Issues 9-10, 2013, p. 342-345.
-
Myamlin S., et al. Testing of railway vehicles using roller rigs. Procedia Engineering, Vol. 187, 2017, p. 688-695.
-
Fomin O., et al. Research of the strength of the bearing structure of the flat wagon body from round pipes during transportation on the railway ferry. MATEC Web of Conferences, Vol. 235, 2018, p. 00003.
-
Tkachenko V., et al. Research of resistance to the motion of vehicles related to the direction by railway. Eastern-European Journal of Enterprise Technologies, Vol. 5, Issues 7-89, 2017, p. 65-72.
-
Okorokov A. M, et al. Research into a possibility to prolong the time of operation of universal semi-wagon bodies that have exhausted their standard resource. Eastern-European Journal of Enterprise Technologies, Vol. 3/7, Issues 93, 2018, p. 20-26.
-
Fomin O., et al. Durability determination of the bearing structure of an open freight wagon body made of round pipes during its transportation on the railway ferry. Communications-Scientific Letters of the University of Zilina, Vol. 21, Issue 1, 2019, p. 28-34.
-
Lovskaya A. A. Peculiarities of computer modelling of strength of body bearing construction of gondola car during transportation by ferry-bridge. Metallurgical and Mining Industry, Vol. 1, 2015, p. 49-54.
-
Zajac R., Řehák K., Prokop A. Investigation of the harmonic response on the simple structure in structural and acoustic domain by experimental and numerical approach. Transport Means, 2018, p. 669-672.
-
Zajac R., Prokop A., Řehák K. Determination of the modal parameters on the thin flat structures. Vibroengineering Procedia, Vol. 18, 2018, p. 91-95.
-
Lovska A. Simulation of loads on the carrying structure of an articulated flat car in combined transportation. International Journal of Engineering and Technology, Vol. 7, Issues 4, 2018, p. 140-146.
-
Blagoveshchensky S. N., Kholodilin A. N. Handbook on the statics and dynamics of the ship. Shipbuilding, Leningrad, 1975, (in Russian).
-
Davidan I. N., Lopatuhin L. I., Rozhkov V. A. Wind and waves in the oceans and seas. Transport, Leningrad, 1974, (in Russian).
-
Kiryanov D. V. Mathcad 13. BHV, Petersburg, 2006, (in Russian).
-
Kondratiev A. V., et al. Relationships between the ultimate strengths of polymer composites in static bending, compression, and tension. Mechanics of Composite Materials, Vol. 52, Issue 2, 2019, p. 259-266.
-
Freight Wagons. General Requirements for the Calculations and Design of New and Upgraded 1520 mm (Non-Self-Propelled) Railcars. DSTU 7598: 2014, 2014, p. 162, (in Ukrainian).
-
Freight Wagons. Strength and Dynamic Quality Requirements. GOST 33211-2014, 2014, p. 54, (in Russian).
-
Railway Applications – Structural Requirements of Railway Vehicle Bodies. – Part 2. Freight wagons. EN 12663-2, p. 54.
Cited by
About this article
This work displays the results of international inter-university research and is also an output of the internal BUT research project Reg. No. FSI-S-17-4104.
