Abstract
Using the finite element method, we investigate the elasto-plastic impact of a rigid sphere on a half-space of auxetic and metal foams. The validity of the Hertz theory for elastic impacts is investigated for both positive and negative Poisson’s ratio. For elastic impacts, the results from Hertz theory are accurate within 20 % with the finite element simulations. The plasticity is modeled using the Deshpande-Fleck metal foam yield criterion. This yield criterion allows for plastic compressibility and can also accommodate materials having a negative Poisson’s ratio. The elasto-plastic simulations reveal that the coefficient of restitution decreases as the impact velocity is increased. The coefficient of restitution is also least for materials having a zero plastic Poisson’s ratio. Our study suggests for maximum energy dissipation the plastic Poisson’s ratio should be close to zero.
1. Introduction
Auxetic materials exhibit superior properties when compared to conventional materials [1]. Recent advancement in the fields of topology optimization and additive manufacturing allows us to design and develop auxetic lattice materials [2]. Consequently, many researchers have investigated the application of auxetic materials for blast and ballistic impact mitigation. These studies are usually performed by modeling the discrete lattice that represents a particular auxetic material [3-5]. For example, Hou et al. [6] compared the crushing strength of auxetic and regular honeycomb structures. They reported that for the same slenderness ratio, the auxetic honeycombs have a higher crushing strength when compared to regular honeycombs. This enhancement was attributed to the auxetic effect, even when the relative density of the auxetic honeycomb was higher when compared to the regular honeycombs.
Recently, the elasto-plastic indentation of auxetic and metal foams has been investigated in detail, where the effect of the yield strain, elastic and plastic Poisson’s ratio, contact friction on the indentation hardness and the ratio of plastic to elastic work was studied [7]. It was shown that the plastic dissipation is least for materials having negative plastic Poisson’s ratio of –1 and that it is maximum when the elastic Poisson’s is close to –1. This indicates that the materials having a plastic Poisson’s ratio close to –1 should have a higher coefficient of restitution in impact scenarios. The objective of the current work is to perform elasto-plastic impact simulations on auxetic materials to identify the effect of the above-mentioned parameters on coefficient of restitution, plastic dissipation and peak force acting on the foam. The results presented will be useful for the design of auxetic materials for blast and ballistic impact mitigation.
2. Problem definition
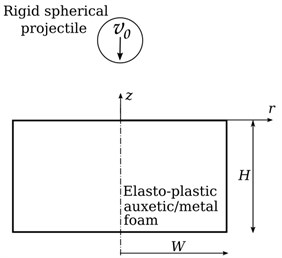
We investigate the axisymmetric impact of an isotropic and elasto-plastic half-space with a rigid sphere of mass m and radius . The sphere has an initial velocity of magnitude and the direction is along axis. The elastic properties of the half-space are defined by the elastic modulus , poisson’s ratio . The principle of virtual work for the axi-symmetric half-space can be written as:
where is the density of the half-space, and are the components of stress and strain tensor, represents the variational operator, is the gap function between the half-space and sphere and is the corresponding Lagrange multiplier. The virtual work equation is discretized in space using six-noded triangular finite elements and solved using the commercial finite element software Abaqus using an explicit time stepping scheme.
The yielding of the metal foam is according to the isotropic Deshpande-Fleck yield criterion [1], which is a two-parameter yield criterion (flow stress and plastic Poisson’s ratio ). The plastic Poisson’s ratio is 0.5 for metals, close to zero for metal foams and negative for auxetic materials. The flow stress is independent of plastic straining (perfect plasticity). The densification of the material is assumed to occur at a strain of 0.5. The yield condition can be written as:
where is the effective stress and is the flow stress. The plastic strain increments are assumed to follow the associated flow rule:
where is the effective plastic strain.
Fig. 1A schematic of the problem under investigation
3. Results
3.1. Elastic impact
As a precursor to the elasto-plastic impact we investigate the elastic impact of a rigid sphere impacting on a half-space. As a reference we discuss the analytical results for the impact of spheres. Usually in this analysis, the velocity of the sphere in contact is calculated by assuming that the contact force can be derived from static calculations and that the velocity of the spheres evolves under the action of this force [2]. This analysis results in the following quantities maximum deflection , maximum force and contact time .
We now proceed to perform finite element simulation of a rigid sphere of radius impacting on an elastic half-space. The Young’s modulus and Poisson’s ratio of the half-space are and . For numerical simulations, the radius and height of the half-space is taken to be . Increasing the size of the half-space beyond does not affect the results. Six-noded triangular elements are chosen to discretize the half-space. The element size near the indenter is 3×10-3, which is sufficient to ensure convergence.
Fig. 2The evolution of various energy components with time during an elastic impact (ν= 0.49). The initial velocity of the sphere is a) v0=0.01C0 and b) v0=0.1C0
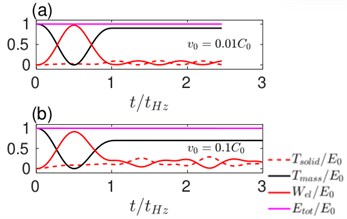
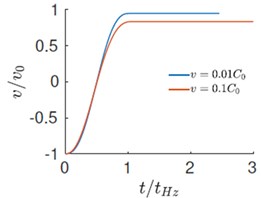
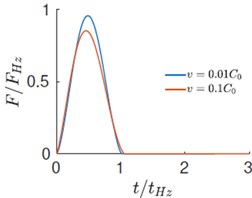
We present simulation results of (nearly incompressible) when the initial velocity of the sphere is and . The evolution of various energies is shown in Fig. 1. Here, , , and represent the kinetic energy of the half-space, kinetic energy of the rigid sphere, strain energy in the half-space and the total energy. All these energies are normalized with respect to the initial energy . The evolution of velocity and contact force with time and the force displacement response is plotted in Figs. 3(a), 3(b) and 3(c) respectively. The time, force and displacement are normalized with , and . The energy evolution shows that even in the case of an elastic impact a fraction of the initial kinetic energy of mass is not recovered. The deficit is lower in the case of low velocity impacts. At higher velocity, a considerable fraction of the initial energy is stored in the form the kinetic and potential energies of the elastic-half space. As a consequence, the coefficient of restitution is larger at lower velocities. The force history reveals that the contact time is for both low and high velocities. i.e., the contact duration is accurately described by the quasi-static estimates. However, since the maximum impact force is less than unity, it is only approximated by the quasi-static estimates. As a reference we also plot the quasi-static load versus penetration curve in Fig. 3(c). For low velocities, both the loading and unloading are adequately represented by the quasi-static theory. However, for higher velocity, we observe considerable hysteresis and a deviation from quasi-static behavior.
Fig. 3a)-b) Evolution velocity and force with time, c) force versus displacement response during impact
a)
b)
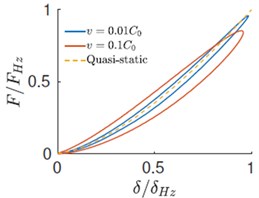
c)
3.2. Elasto-plastic impact
We now present the results for elasto-plastic impact. As a reference case we consider the following properties: yield strain – 10 % and elastic Poisson’s ratio – 0.3 and plastic Poisson’s ratio – 0.49. The evolution of various energies is shown in Fig. 4. We see that as the velocity of impact increases, the plastic dissipation increases. This result is in agreement with the literature.
Fig. 4The evolution of various energy components with time during an elasto-plastic impact (ν= 0.3). The initial velocity of the sphere is a) v0=0.01C0 and b) v0=0.1C0
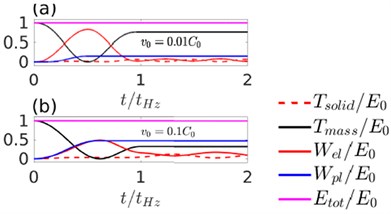
Fig. 5Coefficient of restitution r as a function of velocity for various choices of plastic Poisson’s ratio
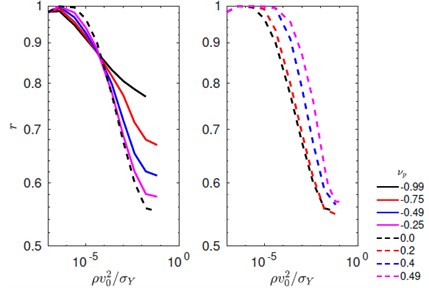
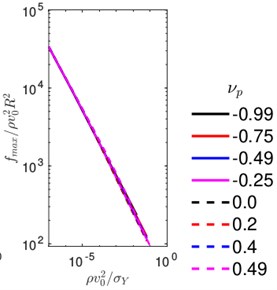
Fig. 6a) Maximum penetration and b) maximum force during impact for various choices of plastic Poisson’s ratio
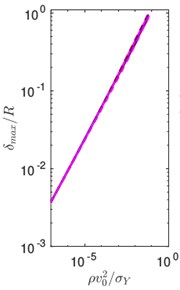
a)
b)
We now perform simulations by varying the velocity and plastic Poisson’s ratio. The coefficients of restitution, obtained from these simulations are shown in Fig. 5, as a function of velocity for various choices of the plastic Poisson’s ratio. When the plastic Poisson’s ratio is increased from –0.99 to 0, the coefficient of restitution decreases. On a further increase of the plastic Poisson’s ratio the value of increases. This indicates that maximum plastic dissipation during an impact happens when the plastic Poisson’s ratio vanishes. We also plot the maximum penetration and maximum force during the indentation for various choices of plastic Poisson’s ratio. It is interesting to note that these quantities are insensitive to the change of plastic Poisson’s ratio.
4. Conclusions
The following conclusions can be made from analysis of elasto-plastic impacts on auxetic materials.
1) For elastic impacts, the estimates obtained from Hertz solution are accurate to about 20 %.
2) The elasto-plastic simulations reveal that the coefficient of restitution decreases as the impact velocity is increased.
3) The coefficient of restitution is also minimum for materials having a zero plastic Poisson’s ratio. Therefore, for maximum energy dissipation the plastic Poisson’s ratio should be close to zero and not be negative.
4) Interestingly, the maximum force and penetration is independent of the plastic Poisson’s ratio.
References
-
Critchley R., et al. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Physica Status Solidi B, Vol. 250, Issue 10, 1963, p. 1982-2013.
-
Wang Fengwen Systematic design of 3d auxetic lattice materials with programmable Poisson’s ratio for finite strains. Journal of the Mechanics and Physics of Solids, Vol. 114, 2018, p. 303-318.
-
Dirrenberger J., et al. Elastoplasticity of auxetic materials. Computational Materials Science, Vol. 64, 2012, p. 57-61.
-
Ghaedizadeh A., et al. Tuning the performance of metallic auxetic metamaterials by using buckling and plasticity. Materials, Vol. 9, 2016, p. 54.
-
Gilat R., Aboudi J. Behavior of elastoplastic auxetic microstructural arrays. Materials, Vol. 6, 2013, p. 726-737.
-
Hou S., et al. How does negative Poisson’s ratio of foam filler affect crashworthiness? Materials and Design, Vol. 82, 2015, p. 247-259.
-
Kumar, et al. Elasto-plastic indentation of auxetic and metal foams. Journal of Applied Mechanics, Vol. 87, Issue 1, 2020, p. 011006.
-
Deshpande V. S., Fleck N. A. Isotropic constitutive models for metallic foams. Journal of the Mechanics and Physics of Solids, Vol. 48, 2000, p. 1253-1283.
-
Johnson K. L. Contact Mechanics. Cambridge University Press, 1985.
