Abstract
The eddy current brake has the advantages of no frictional contact or hydraulic fluid, high structural reliability, etc. The existing linear eddy current brakes are mostly flat type. A cylindrical permanent magnet eddy current brake is proposed in this paper, whose air gap magnetic field is generated by a series of ring-shaped permanent magnets and guided by iron pole to conductor layers, and can achieve higher air gap magnetic flux density. This paper introduces its basic structure and working principle. In order to obtain the analytical model of magnetic circuit design, the equivalent magnetic circuit method is used to analyze and derive the magnetic circuit, and it is verified by the axisymmetric finite element model. To derive the braking force generated by the eddy current brake, the layer theory approach is applied. The influence of electromagnetic parameters on the force characteristic is obtained by finite element numerical calculation, which provides a theoretical basis for the optimal design of the eddy current brake.
1. Introduction
Compared with the traditional brake, the eddy current brake has the advantages of simple working principle, high structural reliability and no friction [1]. It makes the eddy current brake being widely applied, such as high-speed train track braking system and electromagnetic aircraft ejection system braking [2-4]. In order to solve the problem of short-distance braking of a large impulse machinery, a new type of eddy current brake is designed.
The fundamental mechanism of the eddy current brakes has been studied by many scholars [5], and some scholars have analyzed the performances of it with different structures [6]. Jia Qiang has designed a linear eddy current buffer by using Halbach array [7]. Kou Baoquan et al has designed two different kinds of magnetic circuit hybrid eddy current brake [1, 8], which can produce a greater braking force.
For the braking force calculation of the eddy current brake, Romanian scholar Boldea et al. equivalent the primary excitation winding to an infinitely thin current layer, and then derived Expression [9] according to the layer theory. There are also many other different derivation methods for the braking force models of different structures of eddy current buffers [10, 11].
Most of the existing linear eddy current brakes are flat-plate structures or hybrid excitation circuits. This paper designs and analyzes a brake model with a cylindrical structure using only permanent magnet. It has the following advantages over other types of eddy current brakes. First of all, the structure is simple, the installation is convenient, and it is not easy to suffer loss and error. Secondly, a large braking force can be generated, which makes it possible to brake a high-speed moving object in a short time and a short distance.
In order to carry out in-depth research, analytical mode were carried out for magnetic circuit design analysis, and finite element simulation and model analysis were also carried out for eddy current and braking force.
2. Cylindrical permanent magnet eddy current brake model
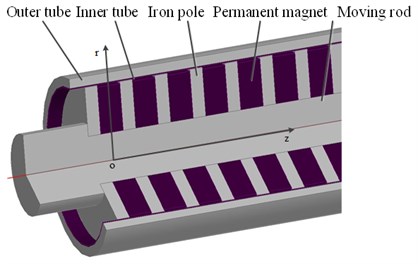
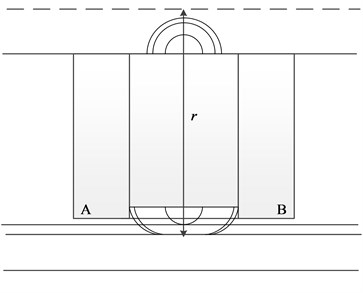
Fig. 1(a) illustrates the partial three-dimensional structural schematic of the studied cylindrical linear EMB, which mainly consists of two parts: the primary part, which consists of a moving rod combined with a sequence of ring-shaped, axially magnetized permanent magnets separated by pure iron poles, and the secondary part, which consists of an outer tube and an inner tube. High-velocity relative movement between the primary and secondary parts will occur under the intensive impact load. Due to the electromagnetic induction, circumferential eddy currents are generated in the secondary. They are sequentially arranged along the iron pole interval, and is opposite to the adjacent eddy currents. At the same time, the circumferential eddy currents induce a new magnetic field interacting with the primary magnetic flux to generate braking force, which hinders the relative motion of the primary and secondary according to Lenz’s law.
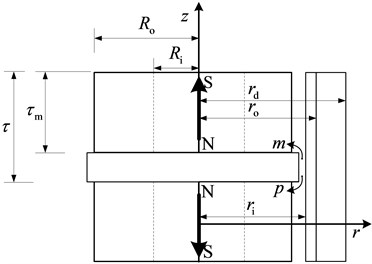
Fig. 1(b) exhibits the layout of the permanent magnets which are oriented with magnetic poles of the same polarity facing each other. The iron pole is located between the two permanent magnets to increase the amount of magnetic flux entering the secondary. Therefore, the decrease of the quiescent operation point caused by the flux leakage in the cylinder hole of permanent magnet and excessive air-gap reluctance is reduced. The thick bold arrows show the direction of field line.
As shown in Fig. 1(b), , , , , , , are the thickness of the permanent magnet; the pole pitch; the internal radius of the inner cylinder; the external radius of the inner cylinder (the internal radius of the outer cylinder), the external radius of the EMB, the internal radius of the permanent magnet, the external radius of the permanent magnet, respectively.
Fig. 1a) Permanent magnet eddy current brake and (b) permanent magnet distribution map
a)
b)
3. Analytical model of the eddy current brake
3.1. Analytical model of no-load magnetic field
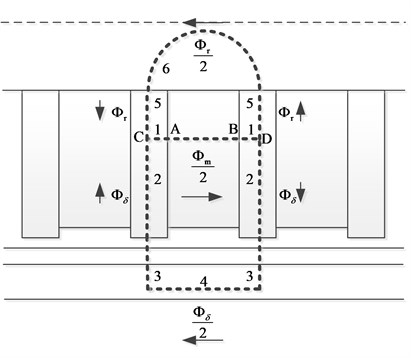
The no-load state of the eddy current brake refers to a state in which the relative velocity of the primary and secondary is zero, that is, the eddy current in the conductor plate is zero. Analyze under no-load condition can rapidly provide verify whether the performance and size are compatible with the envisioned application without involving comprehensive eddy current formulation. Fig. 2(a) shows the magnetic circuit distribution and magnetic flux flow direction of the eddy current brake in the no-load state. This paper did not neglect the leakage flux, adding it into the equivalent magnetic circuit, which improve the accuracy of the analytical model.
The calculation formula for each part of the magnetic circuit is as follows.
The magnetomotive force generated by the permanent magnet is:
where is the permanent magnet coercivity.
The reluctance of the air gap is as follows, and the reluctance of the inner cylinder, the iron pole can be obtained similarly:
where: is the external radius of the iron pole.
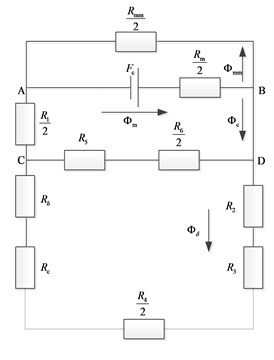
Fig. 2a) Magnetic path and flux flow direction and b) its equivalent magnetic circuit
a)
b)
The magnetic circuit 1 and 4 and the permanent magnet have a ring structure. The reluctance of permanent magnet is as Eq. (3), and the reluctance of the 1 and 4 part can be obtained similarly:
where: is the relative magnetic permeability of the permanent magnet.
The magnetic permeance of the 6 part of the magnetic circuit can be expressed as:
Fig. 3The magnetic circuit of the 6 part
Fig. 4Leakage flux between iron poles
The integral path of the leakage reluctance at the inner and outer ends of the permanent magnet is shown in Fig. 4. Although the relative magnetic permeability of the iron pole is larger than that of the permanent magnet, the axial length of the permanent magnet is longer, thus the magnetically leakage cannot be ignored.
Therefore, the expression of the leakage flux in the hole of the permanent magnet is:
The outer leakage flux is divided into two parts: the part through conductor and part only in the air gap:
The total leakage reluctance of the permanent magnet can be obtained by paralleling the three-part’s leakage reluctance:
According to the equivalent magnetic circuit of the electromagnetic buffer and the Kirchhoff magnetic potential difference law, we can get:
make:
By solving the above equations, we get:
Therefore, the gap magnetic density at the air gap place r under no-load condition is:
The design parameters of the eddy current brake are shown in Table 1.
Table 1Design parameters of eddy current brake
Parameters / mm | Value | Parameters / mm | Value |
The internal radius of the permanent magnet | 20 | The external radius of the inner cylinder | 64 |
The external radius of the permanent magnet | 61 | The external radius of the outer cylinder | 72 |
The external radius of the iron pole | 62.5 | The thickness of the pole pitch τ | 30 |
The internal radius of the inner cylinder | 63 | The thickness of the permanent magnet | 20 |
3.2. Analysis model of braking force
In this chapter, the layer method approach is used to derive the braking force of the inner tube conductor layer. The permanent magnet is equivalent to an infinitely thin current layer so that the magnetic motive force generated by the current layer is equal to the magnetic motive force generated by the actual winding and the permanent magnet. According to the electromagnetic field theory, the corresponding differential equations and their general solutions in different regions can be obtained.
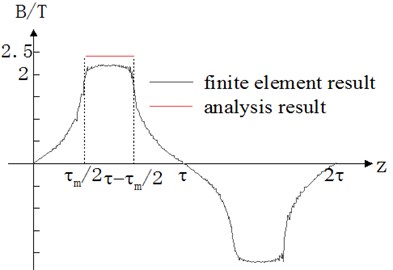
Fig. 5Finite element and analysis results of air gap flux density
For the air gap region, because the electrical conductivity of the air gap is zero, so the equation is as follows. And the region of the outer tube is similar to it:
For the inner tube conductor layer, the eddy current is induced in the layer when the brake is working. And the differential equation in the inner tube layer can be derived:
where is the conductivity (S/m) of the inner cylinder, and is the relative velocity between the primary and secondary.
The expression of the eddy current in the inner tube layer can be derived from the differential equations. And the expression of the eddy current loss and braking force can be obtained:
where is the polar logarithm; is the conjugate complex number of .
4. Finite element analysis
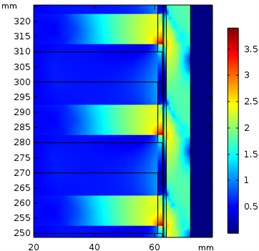
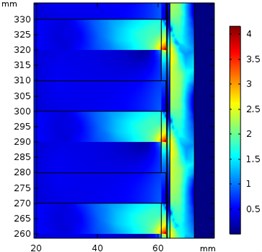
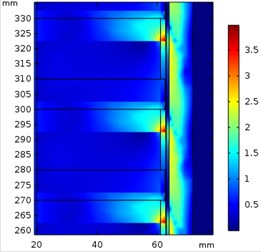
Using a set of design data as Table 1 to establish the finite element model, the magnetic flux density of the device at the speed of 5, 10 and 1 5m/s are as Fig. 6. It is observed that the reaction field of eddy currents tilts the field line coming into the secondary and differs in degree at different speed.
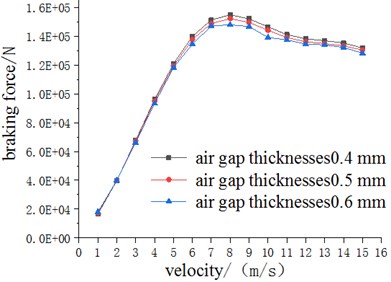
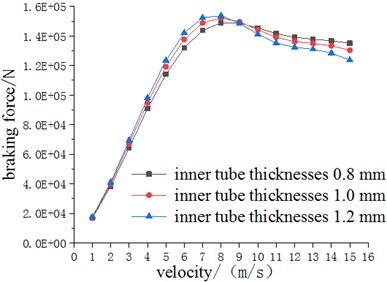
Fig. 7 are force-speed characteristic curves obtained by using different air gap thickness and inner tube thickness, respectively. It can be seen from Fig. 7(a) that the thickness of the air gap has little effect on the braking force when the speed is small, but the larger the thickness of the air gap at a high speed, the smaller the braking force generated, because the air gap flux density is reduced. It can be seen from Fig. 7(b) that both the peak braking force and the critical speed increase as the thickness of the inner tube increases. At the same time, the braking force increases as the thickness of inner tube increases when the speed is less than 9 m/s, but the opposite when the speed is greater than 9 m/s.
In addition, the calculation results show that the peak braking force of the permanent magnet eddy current brake can reach 1.5e5N, and the critical speed is about 8 m/s, which is larger than the ordinary eddy current brake. That is, at high speeds, the brakes can reach a sufficiently large braking force requirement.
Fig. 6Magnetic flux density (T) at a) 5 m/s, b) 10 m/s, and c) 15 m/s
a)
b)
c)
Fig. 7Force characteristic curves for different a) air gap thicknesses and b) inner tube thicknesses
a)
b)
5. Conclusions
In this paper, a new type of cylindrical permanent magnet eddy current brake is proposed, and its basic structure and working principle are introduced. In order to obtain the analytical model of the magnetic circuit, the equivalent circuit method and layer theory approach are used to analyze and derive the magnetic circuit. The model is also calculated by the axisymmetric finite element model, and the analytical model is verified through comparing. The influence of the thickness of the air gap and the thickness of the inner tube on the braking force characteristic curve is obtained using the finite element model, which provides a theoretical basis for the future optimal design of this eddy current brake.
There are still errors of the analytical model proposed this paper with practical device, demagnetization effect of permanent magnet and armature reaction would be added into consideration in future study.
References
-
Kou B., Jin Y., Zhang H., et al. Characteristic analysis of hybrid excitation linear electromagnetic dampers. Proceedings of the CSEE, Vol. 33, Issue 24, 2013, p. 143-151.
-
Wang Z., Hua X., Chen Z. Experimental study on vibration control of a model footbridge by a tiny eddy current tuned mass damper with permanent magnets. Journal of Vibration and Shock, Vol. 33, Issue 20, 2014, p. 129-132.
-
Yan Guobin Study of Hybrid Excitation Rail Eddy Current Brake System of High-Speed Train. Zhejiang University, 2010.
-
Xiao Yao, Wu Jun The analysis and design of permanent-magnet eddy current brake for EMALS. Small and Special Electrical Machines, Vol. 41, Issue 8, 2013.
-
Bae J. S., Hwang J. H., Park J. S., et al. Modeling and experiments on eddy current damping caused by a permanent magnet in a conductive tube. Journal of Mechanical Science and Technology, Vol. 23, Issue 11, 2009, p. 3024-3035.
-
Jang S. M., Lee S. H. Comparison of three types of permanent magnet linear eddy-current brakes according to magnetization pattern. IEEE Transactions on Magnetics, Vol. 39, Issue 5, 2003, p. 3004-3006.
-
Jia Q., Gao Y., Tong Y., et al. Design of linear eddy current buffer. Journal of Engineering Design, Vol. 18, Issue 3, 2011, p. 209-213.
-
Kou B., Jin Y., Zhang H., et al. Analysis and design of hybrid excitation linear eddy current brake. IEEE Transactions on Energy Conversion, Vol. 29, Issue 2, 2014, p. 496-506.
-
Boldea I., Babescu M. Multilayer theory of D.C. linear brakes with solid-iron secondary. Proceedings of the Institution of Electrical Engineers, Vol. 123, Issue 3, 1976, p. 220.
-
Yin Xiangrui Research on Long Stroke Secondary Moving Permanent Magnetic Linear Eddy Current Brake. Harbin Institute of Technology, 2017.
-
Zhao Xiaobo Study on Electromagnetic Properties and Braking Performance of Permanent Magnet Type Eddy Current Retarder. Nanjing Agriculture University, 2009.
