Abstract
Fatigue has been related to changes in the time-variability properties of coordinative variables during an exhausting isometric exercise [1]. In this study we aimed to investigate the qualitative changes in acceleration (kinematic collective variable) during exhausting running ( 8) and ski mountaineering ( males = 5, females = 5) exercises. Time-variability of acceleration was calculated using the Multifractal Detrended Fluctuation Analysis (MFDFA). Initial and final time series of both exercises were compared through Wilcoxon test. A reduction of MFDFA spectrum was observed in the final period in both exercises while the participants approached exhaustion, except for the male group of ski mountaineers that increased their speed at the end of the exercise. In runners, those who approached the psychobiological exhaustion showed a higher reduction in the MFDFA spectrum compared to those who did not. Although more research is needed to model this dynamic behavior in front of different constraints, time-variability of acceleration throughout a multifractal application seems to provide a valid information about the system adaptation during exhausting dynamic exercises.
1. Introduction
The study of the time-variability properties, widely used in scientific fields to investigate the complex systems behavior, has revealed changes in the structure of several collective variables during exercise [1-3]. The dynamic behavior of such collective variables informs about the temporal coupling of the system’s components, and the ability of the system to control its behavior [1]. It has been investigated under different constraints (e.g., diseases, stress, etc.) to study phenomena as the self-organization and the interactions of processes across different levels and timescales: from micro- (e.g., cellular, etc.) to macro-timescales (e.g., psycho-emotional, etc.) [4-6]. Multifractal Detrended Fluctuation Analysis (MFDFA) has been used to identify the deviations in the fractal structures of the variability within time periods with large and small fluctuation, and thereby allowing to study this dynamic behavior [4, 5, 7].
A rapid and flexible control of the system’s timescales has been demonstrated at kinematic level in high-skilled athletes, who are able to coordinate better their movements and have a higher effectivity and task performance [8-10]. On the contrary, a rigid and slower control of the component’s interactions characterizes the less skilled and experienced performers, as well as less coordinated and efficient.
Taking fatigue as common constraint in exercise performance, it has shown how produces maladjustments of the timescales’ dynamics [1-3, 11]. In that sense, it has been observed how participants lost their initial fine regulation and control during a quasi-isometric exercise (i.e., static task), disabling over time the task performance, as they approached exhaustion [1, 11]. However, the time-variability of kinematic variables during dynamic exercises performed until exhaustion has not been studied yet. This information can be useful in terms of training and health monitoring. Concretely, it can help to detect the coordinative changes and loss of control produced by the exercise induced fatigue and anticipate the exhaustion point. It is worth to point that although this type of analysis has been applied to evaluate physiological processes and diagnose diseases [5], its applications to monitor sport and exercise activities is still scarce.
Accordingly, this study, divided in two parts, aimed to investigate the qualitative changes of the time variability of a kinematic collective variable, such as the acceleration, during two competitive and maximal (exhausting) dynamic exercises in runners and ski mountaineers.
2. Methods
– Running exercise: Eight experienced runners (39.37 ± 6.19 y.o.) performed a Cooper Test covering the maximum distance in 12 min.
– Ski mountaineering exercise: Ten ski mountaineering athletes (5 males and 5 females; 25.8 ± 5.3 y.o.) competing at international level performed a trial vertical race (1980 m of distance and 415 m of positive gain). Following the federation’s rules, the groups competed separately in function of the gender.
The athlete’s acceleration was recorded using WIMU devices (Realtrack Systems SL, Almería, Spain) placed on L3 [12]. The sample frequency was 100 Hz. The time series of acceleration were analysed through MFDFA [7]. The first and last minute of exercise were compared in the runners, and the first and third portion of the time series were compared in the ski mountaineers. Each portion contained 30000 data points (males group), and 41900 data points (females group). Velocity was also calculated and recorded during these periods to compare the performance in both running and skiing exercises.
The differences between initial and final periods of the MFDFA spectrum were analysed with the Wilcoxon non-parametric test while it was also calculated the subtraction’s differences between final and initial values of MFDFA spectrum and velocity. Heart Rate (HR) was continuously recorded in both exercises to assess the physiological stress and the Borg’s RPE (CR-10) was monitored only at the end of the running exercise. Data analysis was conducted via Matlab© R2013b and SPSS.
3. Results
Both competitive exercises supposed a high psychobiological stress (HR running = 181.75 ± 9.31; RPE running = 8.38 ± 0.74; HR skiing = 187.23 ± 10.05) for the athletes. The results showed a reduction in the MFDFA spectrum of the acceleration time series (see example in Fig. 1) in both exercises as the effort accumulated, even though no significant differences were found between the first and the last period of exercise during running ( Wilcoxon = –1.402, 0.161) and ski mountaineering ( Wilcoxon = –1.38; 0.17).
Fig. 1Example of how the MFDFA of the acceleration spectrum was reduced from the initial to the final period of exercise
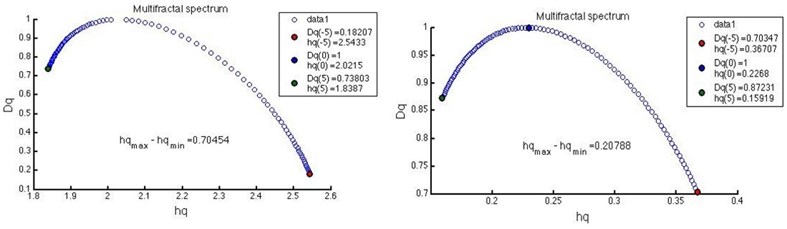
In the running study, those who approached exhaustion ( 4; RPE ≥ 9; Average HR ≥ 180) showed higher reduction (0.28) in the MFDFA of the acceleration spectrum at the end of the exercise, compared with those who reached less psychobiological stress ( 4; RPE < 9; Average HR < 180) with a reduction of 0.09. The loss of velocity between the initial and final period of the run matched with a reduction in the MFDFA of the acceleration spectrum (Table 1).
In the skiing exercise, gender groups followed different strategies during the race. While the female skiers group showed a reduction of the MFDFA of the acceleration spectrum and a velocity decrease at the end, the male group displayed a small increment of the MFDFA spectrum, probably due to a lower slope in the final part of the trial and reflected in an increase of the velocity (Table 1).
Table 1Multifractal Detrended Fluctuation Analysis (MFDFA) spectrum of the acceleration and velocity of the first and last periods of the running and ski mountaineering exercises and their differences
Runners ( 8) | Male ski mountaineers ( 5) | Female ski mountaineers ( 5) | |
Initial MFDFA spectrum | 0.37 ± 0.24 | 0.30 ± 0.06 | 0.49 ± 0.24 |
Initial Velocity (m/s) | 4.10 ± 0.31 | 1.39 ± 0.04 | 1.22 ± 0.07 |
Final MFDFA spectrum | 0.19 ± 0.05 | 0.53 ± 0.17 | 0.47 ± 0.10 |
Final Velocity (m/s) | 3.79 ± 0.27 | 1.48 ± 0.07 | 1.12 ± 0.04 |
MFDFA spectrum differences | –0.18 ± 0.19 | 0.23 ± 0.11 | –0.02 ± 0.14 |
Velocity differences | –0.31 ± 0.04 | 0.09 ± 0.03 | –0.10 ± 0.03 |
These results are in accordance with previous studies during an isometric exercise [1, 11]. The reduction in the variability of the collective variable suggests a reduced adaptability to the task demands over time due to the accumulated effort and for hence a more difficult control of the task.
4. Conclusions
The time-variability of acceleration seems to provide a valid information about the system adaptation during exhausting dynamic exercises. More evidences are needed to model the way the collective variable changes its behaviour and how the system loses its control at different scales as a consequence of fatigue during exercise.
In future research, constraints that can affect the kinematic variability, such as the slope or the terrain, should be carefully controlled. The multifractal analysis of the acceleration time-variability points towards being a useful tool for monitoring and evaluating the adaptation to exercise. In this sense, it may complement the commonly used quantitative variables (e.g., HR or lactate values) in the control of training and competition. Such multifractal analysis may be applied as well to other variables with medical purposes.
References
-
Vázquez P., Hristovski R., Balagué N. The path to exhaustion: Time-variability properties of coordinative variables during continuous exercise. Frontiers in Physiology, Vol. 7, 2016, p. 37.
-
Cashaback J. G., Cluff T., Potvin J. R. Muscle fatigue and contraction intensity modulates the complexity of surface electromyography. Journal of Electromyography and Kinesiology, Vol. 23, 2013, p. 78-83.
-
Pethick J., Winter S. L., Burnley M. Fatigue reduces the complexity of knee extensor torque fluctuations during maximal and submaximal intermittent isometric contractions in man. Journal of Physiology, Vol. 593, 2015, p. 2085-2096.
-
Dutta S., Ghosh D., Chatterjee S. Multifractal detrended fluctuation analysis of human gait diseases. Frontiers in Physiology, Vol. 4, 2013, p. 274.
-
Cleetus H. M. M., Singh D. Multifractal application on electrocardiogram. Medical Engineering and Technology, Vol. 38, Issue 1, 2014, p. 55-61.
-
Wijnants M. L. A review of theoretical perspectives in cognitive science on the presence of scaling in coordinated physiological and cognitive processes. Journal of Nonlinear Dynamics, Vol. 12, 2014, p. 962043.
-
Ihlen E. A. Introduction to multifractal detrended fluctuation analysis in Matlab. Frontiers in Physiology, Vol. 3, Issue 141, 2012, https://doi.org/10.3389/fphys.2012.00141.
-
Den Hartigh R. J., Cox R. F., Gernigon C., Van Yperen N. W., Van Geert P. L. Pink noise in rowing ergometer performance and the roll of skill level. Motor Control, Vol. 19, Issue 4, 2015, p. 355-369.
-
Nourrit Lucas D., Tossa A. O., Zélic G., Delignières D. Learning, motor skill, and long-range correlations. Journal of Motor Behavior, Vol. 47, Issue 3, 2014, p. 182-189.
-
Terrier P., Dériaz O. Persistent and anti-persistent pattern in stride-to-stride variability of treadmill walking: Influence of rhythmic auditory cueing. Human of Movement Science, Vol. 31, 2012, p. 1585-1597.
-
Hristovski R., Balagué N. Fatigue-induced spontaneous termination point-Non equilibrium phase transitions and critical behavior in quasi-isometric exertion. Human Movement Science, Vol. 29, Issue 4, 2010, p. 483-493.
-
Schütte K. H., Aeles J., De Beéck T. O., Van Der Zwaard B. C., Venter R., Vanwanseele B. Surface effects on dynamics stability and loading during outdoor running using wireless trunk accelerometry. Gait and Posture, Vol. 48, 2016, p. 220-225.
