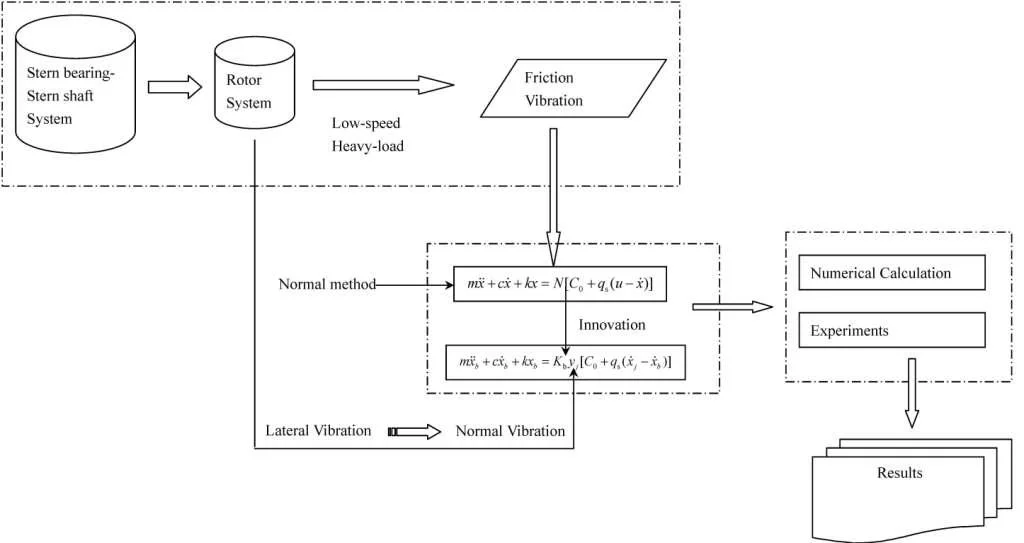
Abstract
During the slow voyage of ships, the friction-induced vibration noise often occurs in the contact region of the water-lubricated stern bearing and the tail shaft. The lateral vibration can impact the normal motion of the contact surface, then change the dynamic friction force, finally affect the behaviour of the friction-induced vibration. By adding the movement of the stern shaft journal into the normal load description of the dynamic friction, the equation of friction-induced vibration considering the effect of normal vibration was established. Then the effect law of normal vibration on friction-induced vibration was discussed by numerical simulation and test. The results show that the normal vibration would make the friction-induced vibration appear quasi-periodic, chaotic trend, and narrow the speed range in which the noise of friction-induced vibration appears.
Highlights
- Established a new equation of friction-induced vibration considering the effect of lateral vibration
- Discussed the effect law of lateral vibration on friction-induced vibration
- The lateral vibration of the stern shaft journal would make it appear quasi-periodic and chaotic trend
- The lateral vibration of the stern shaft journal narrows the speed range in which the friction-induced vibration appears
1. Introduction
As an essential part of the shafting of the underwater vehicle, the water-lubricated stern bearing plays a significant role in the rapidity, security, concealment and survival ability of navigation. Due to the complex load of the stern shaft, it is difficult to establish dynamic pressure lubrication between the shaft and bearing in a start-stop period and the low-speed operation, so, the partial areas have entered the boundary lubrication state. When the shaft and bearing contacted, the slippage effect in these regions would cause friction vibration, which might produce low-frequency trill and high frequency howling [1]. As the underwater vehicle has some special requirements for the covert and viability, some situation, such as the trilling of the stern bearing when the propeller speed is less than 0.3 m/s, and howling when less than 0.5 m/s [2], should be avoided as far as possible.
Friction vibration is a widespread physical phenomenon. The squealing of the braking system when the car is braking, or the plane is landing is a typical frictional vibration phenomenon [3]. For the water-lubricated bearing, the viscoelastic nature of the polymer material determines that the friction between the bearing and the metal shaft has different mechanism and characteristics [4]. T. A. Simpson and R. A. Ibrahim [5] discussed the mechanism of friction-induced vibration of water-lubricated radial rubber bearing. It was pointed that under the condition of lower speed rotation, especially at the instant of the start and stop, the lubrication condition of bearing was bad, mostly in the dry friction, and the self-excited vibration and noise was easy to appear. But with the increase of rotational speed, the situation was improved. Peng [6] has studied the frictional vibration produced by the water-lubricated rubber stern bearing at low speed, and the results show that although the rubber bearing had small friction coefficient, wear resistance, buffering, suppression, not sensitive to install and impact, but in the case of considerable pressure the wear of rubber body was severe, and under the specific speed the friction vibration was apparent, and the singing sound also came. The singing sound test of water-lubricated rubber stern bearing, conducted by Y Z TIAN, et al. [7], showed that the singing sound of the stern rubber bearing did not present certain regularity, and the response of vibration behaved a strong nonlinearity. The contact area between the shaft neck and the bearing and the amount of negative slope of the friction coefficient-velocity curve determined whether the singing sound of stern rubber bearing could appear in operation.
For the coupling research on the friction behaviour of stern bearing and the vibration of shafting, Ryzhik [8], based on the system consisting of a flexible plate and two rigid surfaces, analyzed the incentive mechanism of friction vibration. He summarized that the transverse vibration of the plane affected the normal force, then friction force changed, and these changes affected the transverse vibration of the plane in turn. Finally, this feedback caused instability. Mihajlović [9], using the pipe system, discussed the torsional vibration and the transverse vibration of the flexible rotor considering the friction vibration, and concluded the relationship between the friction-induced vibration and the eccentric mass induced vibration. Through analyzing flexible rotor system, L. P. Li [10] found the unbalance distribution had a significant influence on the behaviour of the friction vibration, and the rotor vector of friction vibration, with the second-order and above of unbalance distribution, could be reversed to the rotation, or same to the rotation. Kaikai C. H. E. et al. [11], applied the distribution support model and speed dependent Stribeck friction model to establish shafting dynamic model considering friction excitation with the Lagrange equation and the modal expansion method. The numerical simulation research on the relationship between shafting nonlinear vibration and physical parameters showed that under the same coefficient of friction, contact force, and rotary speed, the inclined bearing was more likely to causes self-excited instability of shaft system. F. Chen et al. [12], Z. G. Zhang, et al. [13], also established the dynamic model of shafting under friction excitation, based on the Lagrange equation, to study the effects of shafting dynamics on friction behaviour. Ch Yang et al. [14], Applied the finite element method and the substructure modal analysis to establish the finite element model and substructure coupled model of the shaft-shell coupled structure, and to study the dynamic characteristics of that system under the friction excitation. He concluded that the self-excited oscillation was more easily produced with the higher friction coefficient, the smaller damping ratio, and the lower speed. Ch X. Xiong et al. [15], based on the viscous-sliding mechanism of friction-induced vibration and negative damping theory, established a 9-DOF journal-bearing friction plane model and gave the structure vibration response under constant rotation excitation.
In summary, the friction vibration will change the force of the stern shaft journal, that is, except for the dynamic and static load, there is the continually evolving dynamic friction. In the occurring process of friction vibration, the movement of the normal direction of the contact surface has a significant influence on the change of the friction. Meanwhile, a lot of tests [8, 16] have shown that the changes in displacement, velocity, and other sports, resulted from the vibration of the same direction would affect the normal force, and then changed the friction. In the course of low-speed navigation, due to the excitation from the outside, the shafting generates lateral (whirl) vibration, which will undoubtedly change the normal motion of the friction interface. Current researches on the water-lubricated bearing friction vibration mostly ignored the influence of lateral vibration on normal pressure in the discussion of dynamic friction. In this article, the movement of the stern shaft neck is added in the normal load description of the dynamic friction, and the coupled lateral and friction vibration is established to analyze the effect of transverse vibration on the friction vibration of the water-lubricated bearing by numerical simulation and experiment.
2. Analysis
2.1. Fundamental equations
In the case of friction vibration of water-lubricated tail bearing, local contact between the stern bearing and stern shaft journal occurs. According to the analysis conclusion of Krauter and Smith [17], the movement between the stern bearing and stern shaft journal can be simplified as friction behaviour between a slat and sliding block, as shown in Fig. 1.
Fig. 1Simple model of friction-induced vibration
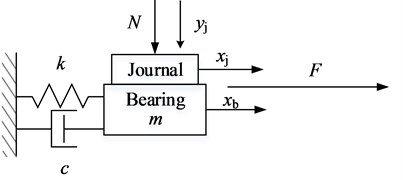
In the simple model, the journal is sliding on the surface of the bearing by the velocity of , and the relative velocity between the journal and the bearing is . The dynamic friction is , and the load on the bearing is . The mass, stiffness and damping coefficient of the bearing is , and . The effect of transverse vibration is presented by the normal motion of journal . Thus, the motion equation of the bearing slat can be expressed as:
where, the mathematical description form of dynamic friction is the problematic point in the study of friction vibration, and at present, it mainly consists of these following ways:
(1) Taylor series [5].
Supposing , the right side of the Eq. (1) is expanded to the Taylor series according to the power of , and the following formula can be obtained after eliminating the high-order trace:
Generally, the motion of the bearing slat is micro-amplitude vibration. Therefore, the vibration equation of the bearing slat can be obtained without considering the minor term above the second order in Eq. (2) and the constant term irrelevant to vibration, as shown in the following equation:
The stability of friction vibration of the bearing slat can be discussed by using this equation.
(2) Polynomial.
Bannerjee et al. [18] proposed a hypothesis of quadratic polynomials, believing that the relationship between dynamic friction and sliding speed is:
where, is the dynamic friction force; is the maximum static friction force; , is the experimental constant; is relative sliding speed.
(3) Empirical formula.
Frictional vibration generally occurs at lower relative velocities. Therefore, some empirical formulas of frictional force can be obtained based on coulomb's law of friction. As suggested by Smith, the friction force of water-lubricated bearing is qualitatively related to axial angular velocity [5]:
where, is the normal load of bearing; is the unit inverse velocity constant; and are respectively the static and dynamic friction coefficients; is the radius of the shaft disc; is the axial angular velocity in contact with the stern bearing.
Some researchers also introduced a more simplified empirical formula [19]:
where, refers to the positive pressure between the bearing and the contact surface of the shaft; is the system stiffness; is system damping; is the constant related to the initial condition; is the slope of the relation curve between the friction coefficient and the speed measured by the bearing friction performance test; is the relative velocity between contact surfaces.
In the above mathematical descriptions of the dynamic friction force , the positive pressure of the sliding block on the slat remains unchanged. But in the course of friction vibration of the stern bearing, the sliding block simplified from the journal is actually in response to the lateral vibration. Thus, the displacement in the normal direction is variable, and then the positive pressure of the block on the slat is not constant. With this, referring on the above empirical formula, the motion equation of friction vibration of the stern bearing, considering the response of transverse vibration of the stern shaft, can be obtained:
where, is the compression stiffness of the stern bearing.
2.2. Numeric calculation
The numerical calculation is based on the performance test of a water-lubricated stern bearing conducted on the comprehensive performance test platform of the ship shafting system of Wuhan University of Technology, and the test results are shown in Table 1. The other test parameters involve: the stern shaft diameter is 185 mm; the length is 5 m; the stern bearing is 608 mm long; the pressure is 0.2 MPa; the room temperature is 30 ℃.
Table 1Results of performance test of stern bearing
Rotation speed / (r·min-1) | Friction coefficient | Slope | Velocity / (m·s-1) |
489 | 0.115 | 4.73 | |
423 | 0.113 | 2.727×10-5 | 4.10 |
222 | 0.109 | 2.289×10-5 | 2.15 |
196 | 0.108 | 2.037×10-5 | 1.89 |
141 | 0.118 | –0.000 182 6 | 1.37 |
87 | 0.158 | –0.000 722 5 | 0.83 |
54 | 0.215 | –0.001 775 0 | 0.52 |
43 | 0.248 | –0.003 055 0 | 0.42 |
33 | 0.295 | –0.004 245 0 | 0.31 |
27 | 0.324 | –0.005 782 0 | 0.26 |
22 | 0.391 | –0.011 210 0 | 0.20 |
The approximate formula of friction coefficient can be obtained by fitting the quadratic polynomial according to the test data:
According to the above formula, the initial parameter can be obtained: is 0.409.
In order to simplify the calculation, the bearing slat is simplified into a unit mass block, and the system stiffness is the unit stiffness, and according to the calculation formula of damping in reference [20], the system damping is very small, then the damping can be ignored. So, , 1, . Besides, supposing the bearing composition stiffness is also equal to 1, and the normal motion of journal is the stable sinusoidal periodic response, , where is amplitude, and is response frequency, then the final equation of the mass is:
Let , , , the Eq. (9) can be reduced to first-order differential equations:
Then, when the other initial conditions are determined, using the ODE45 function of Matlab libraries, the results of the numerical calculation could be obtained.
2.3. Experiments
The propulsion shafting experimental system at the Wuhan University of Technology has been designed and established in 2012. The test platform is mainly composed of frequency conversion motor, the decelerator, thrust bearing, propulsion shafting, the foundation and the base, also equipped with water lubrication system, oil lubrication system, hydraulic loading system and state monitoring system, which can display the friction coefficient, temperature, and pressure of tested bearings. The platform can carry out the research of propulsion shafting dynamics, shafting vibration, bearing and sealing performance test, etc. The tests of the coupled system dynamic behavior were carried out on this platform and the sensors gathering the bearing vibration and orbit of the stern shaft are shown in Fig. 2.
Fig. 2The sensors installation

a) Vibration sensors

b) Orbit sensors
The lubricating medium of this test is water, with the temperature 30 °C, the bearing pressure 0.20 MPa, the flow rate 30 L/min. After the running-in state for 50 hours, the expect experiment of lateral vibration on friction vibration was carried out. Because the shafting of the test platform is longer and the start torque is big, it is not easy to control the run-up process in the low-speed range. Therefore, this test chose to record the friction coefficient at a specific speed and the associated vibration signals in the slow run-down process.
Table 2Corresponding conversion table of speed
Motor speed / (r·min-1) | |||||||
40 | 50 | 60 | 80 | 100 | 160 | 260 | |
Shaft speed / (r·min-1) | 22 | 27 | 33 | 43 | 54 | 87 | 141 |
Journal velocity / (m·s-1) | 0.20 | 0.26 | 0.31 | 0.42 | 0.52 | 0.83 | 1.37 |
The variation of lateral vibration was simulated by loading with bearing pressure 0.20 MPa, and no-load, because when the load changes, the response amplitude of the stern shaft journal changes accordingly, then the influence on the friction vibration can be observed.
During the test, the speed record points are that whose slope is negative in Table 1, which is 22, 27, 33, 43, 54, 87 and 141 rpm, and the corresponding transformation of the speed representation method with other shafting is shown in Table 2.
3. Results and discussion
3.1. Friction-induced vibrations
When friction-induced vibration occurs, peak groups generally appear in the intermediate frequency region [21], as shown in Fig. 3, which is the vibration frequency spectrum diagram in the horizontal direction when the shaft speed is 87 r·min-1. From this diagram, it can be seen that there were some small-peak groups in the range from 1.1 kHz to 1.6 kHz, which is response region of the friction vibration, and some apparent harmonic amplitude in the range lower than 800 Hz, which is the response region of the lateral vibration. Besides, from the corresponding time-domain diagram, as shown in Fig. 4, it can be seen that the apparent noise groups appear. Furthermore, from the orbit of shaft center, as shown in Fig. 5, it is clear that the journal began to contact with the bearing, and a jagged sharp angle appeared in the bottom-right corner of the axis trajectory, which is typical rubbing characteristics.
Fig. 3The vibration frequency spectrum diagram in the horizontal direction
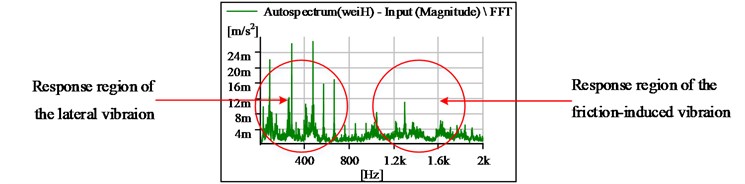
Fig. 4The time-domain spectrum
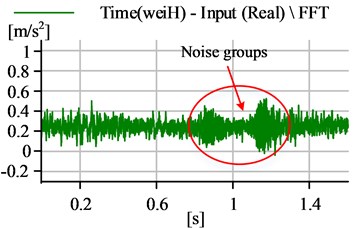
Fig. 5Orbit of shaft centre
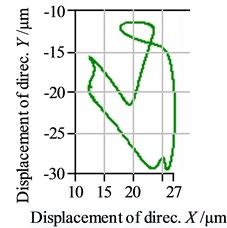
From the above analysis, it can be determined that the friction-induced vibration appeared at that point of the negative-slope area. Meanwhile, the stern bearing-shaft system is always in the state of misalignment and unbalance because of the apparent harmonics and the flat crescent-shaped axis trajectory. As the misalignment and unbalance are the main factors causing lateral vibration of the stern shaft, the motion morphology of friction-induced vibration is affected by the lateral vibration in the whole negative-slope area.
3.2. Influence of lateral vibration on the motion morphology of friction-induced vibration
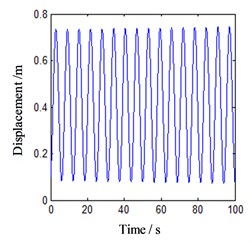
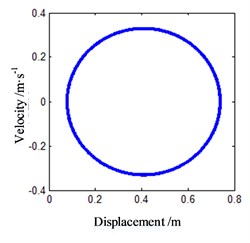
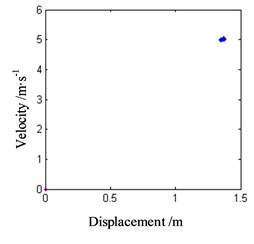
Firstly, the effect of lateral vibration on dynamic friction is not considered. When the friction-induced vibration occurs, the normal motion of journal is set as a constant unit displacement, that is 1. Select the speed point 0.83 m/s, with is –0.000722545 and set the initial motion value of the vibration Eq. (10) as (0.1, 0.1), then the results of the numerical analysis within 100 s are shown in Fig. 6.
Fig. 6Motion morphology of friction-induced vibration equation without considering lateral vibration
a) Vibration displacement in horizontal direction
b) Phase trajectory in horizontal direction
c) Poincare map in horizontal direction
From the figure, it can be seen that after 100 s passes on, the motion form of the unit mass block is still stable, and the phase point on the phase trajectory is always on the stable limit ring. The Poincare map also shows that the motion of the block belongs to the periodic motion. This indicates that the friction-induced vibration state at this speed point is stable, and the system will be in a continuous periodic vibration state and radiate frictional noise outwards.
Subsequently, the effect of lateral vibration on dynamic friction is considered. For example, the response amplitude is set as 1 m, and the response frequency is set as 10 Hz. Also, select the speed point 0.83 m/s, with is –0.000722545, and set the initial motion value of the vibration Eq. (10) as (0.1, 0.1), then the results of the numerical analysis within 100 s are shown in Fig. 7.
Fig. 7Motion morphology of friction-induced vibration equation with A= 1 m and w= 10 Hz
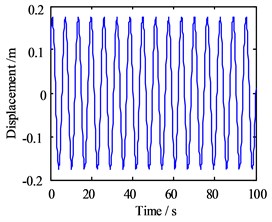
a) Vibration displacement in horizontal direction
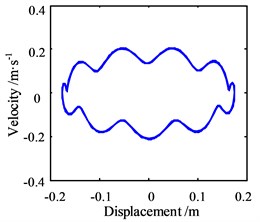
b) Phase trajectory in horizontal direction
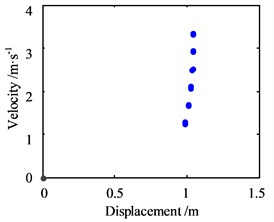
c) Poincare map in horizontal direction
Same as the motion without considering the lateral vibration response, the vibration displacement has no apparent decrease because of the minimal negative slope. Still, the phase trajectory shows that the lateral vibration periodic response of the journal indeed affects the friction-induced vibration of the unit mass block of the bearing slat, and the motion of the block becomes more complex, with the periodic effect on the trajectory. Besides, the Poincare map shows that the motion becomes the quasi-periodic state, and this phenomenon indicates that the motion is no longer stable.
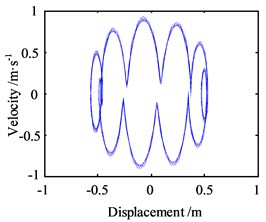
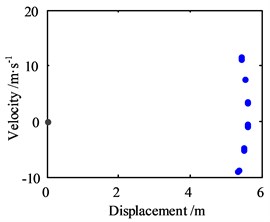
For further analyzing the influence of the amplitude of lateral vibration response, the response amplitude is set as 10 m, and the other parameters are same as before, then the results of the numerical analysis within 100 s are shown in Fig. 8.
Fig. 8Motion morphology of friction-induced vibration equation with A= 10 m and w= 10 Hz
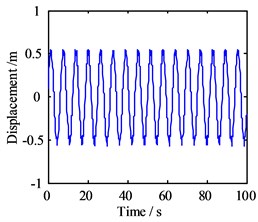
a) Vibration displacement in horizontal direction
b) Phase trajectory in horizontal direction
c) Poincare map in horizontal direction
With the amplitude increasing, the vibration displacement of the block also increases accordingly, and the phase trajectory and the Poincare map show the same form as the amplitude is 0, only with bigger value. It means that the variation of the amplitude of lateral vibration response makes the motion of friction-induced vibration of the block more complex and bigger, but no affections on the form of it.
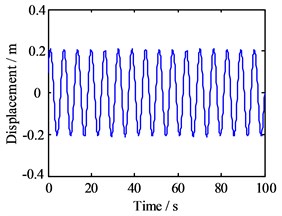
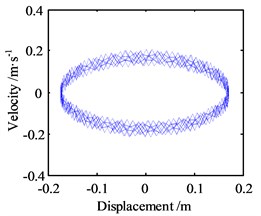
Next, with the amplitude, still 10 m, the response frequency is changed to 100 Hz, and the other parameters are same as before, then the results of the numerical analysis within 100 s are shown in Fig. 9.
From this figure, it can be seen that the vibration displacement of the block is still stable, but the phase trajectory shows that the mass block is in a more complex motion on a loop, and the Poincare map also presents that the motion has fractal characteristics of the chaotic state. Therefore, this means that the higher frequency component of the lateral response tends to disturb the friction-induced vibration and cause it to collapse.
From the above analysis, it can be concluded that the normal vibration on the unit mass block will aggravate the amplitude of its friction-induced vibration. At the same time, it tends to periodize, and even chaos the motion of the block, and this trend will make it impossible to maintain a steady-state of friction-induced vibration. The friction-induced vibration will also not be detected anymore.
Fig. 9Motion morphology of friction-induced vibration equation with A= 10 m and w= 100 Hz
a) Vibration displacement in horizontal direction
b) Phase trajectory in horizontal direction
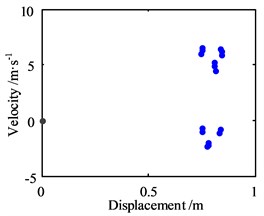
c) Poincare map in horizontal direction
3.3. Influence of lateral vibration based on the different-loading tests
When the test bench is in the condition of the different-loading, the lateral vibration of the stern shaft is different. Here is an example, which is the vibration frequency spectrum diagram in the horizontal direction with zero-load, , as shown in Fig. 10(a), and loading with bearing pressure 0.20 MPa, as shown in Fig. 10(b), when the shaft speed is 87 r·min-1.
From the figure, it can be seen that Fig. 10(b) has more higher-frequency components and the bigger amplitude in the response region of the lateral vibration, and this means that the condition of loading can have the stronger effect than zero-load on the friction-induced vibration. Hence, from the perspective of the experiment, the effect of lateral vibration on friction-induced vibration can be observed by changing the load to get the variation of amplitude in the response region of the friction-induced vibration. The peak value of the friction region in the horizontal direction with every speed point, as listed in Table 2, was recorded under zero-load and bearing pressure 0.20 MPa. The variation curve is shown in the Fig. 11.
Fig. 10The vibration frequency spectrum diagram in the horizontal direction
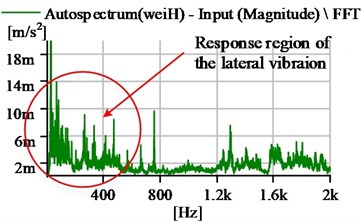
a) Zero load
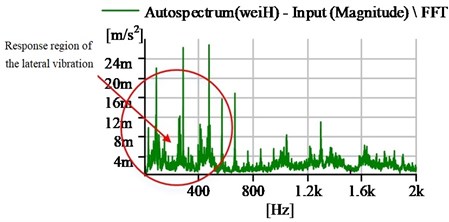
b) Bearing pressure 0.20 MPa
Fig. 11The variation curve of peak value in the friction region
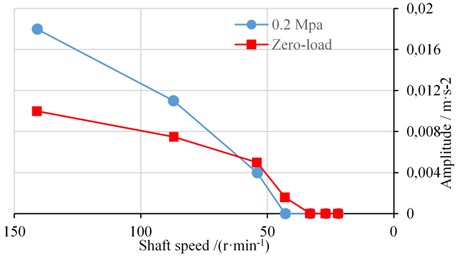
From this above variation curve, obtained by collating the test data, it can be observed that the amplitude decline rate in the friction region is relatively higher under the load of 0.2 MPa, and especially the amplitude cannot be detected when it is down to 43 rpm, while there is still data under no-load conditions. The test result indicated that the increase of load compresses the speed range where the friction-induced vibration occurs in the stern bearing-shaft system. The test result is also consistent with the above numerical analysis results that the effect of lateral vibration has the tendency of quasi-periodic and chaotic friction vibration and makes it unstable. Therefore, for the underwater vehicle, which often operates in the low-speed zone, the stern bearing-shaft system can reduce the noise intensity caused by friction-induced vibration more under load conditions.
4. Conclusions
Totally, by adding the movement of the stern shaft journal into the normal load description of the dynamic friction, the equation of friction-induced vibration considering the effect of lateral vibration was established, and the effect law of lateral vibration on friction-induced vibration was discussed by numerical simulation and test, and the following conclusions are obtained:
1) The lateral vibration of the stern shaft journal will aggravate the amplitude of the stern bearing’s friction-induced vibration, with the tendency to periodize and even chaos the motion of the friction-induced vibration. This trend will make it impossible to maintain a steady-state of friction-induced vibration, and the friction-induced vibration will also not be detected anymore.
2) The increase of load compresses the speed range where the friction-induced vibration occurs in the stern bearing-shaft system. For the underwater vehicle, which often operates in the low-speed zone, the stern bearing-shaft system can reduce the noise intensity caused by friction-induced vibration more under load conditions.
References
-
Qin H. L., Zhou X. C., Yan Z. M., et al. Effect of thickness and hardness and their interaction of rubber layer of stern bearing on the friction performance. Acta Armamentarii, Vol. 34, Issue 3, 2013, p. 318-323.
-
Yao S. W., Hu Z. C., Ma B., et al. The new development of rubber bearing and its application in warships. Ship Science and Technology, 2005, p. 27-30.
-
Eriksson M., Jacobson S. Friction behavior and squeal generation of disc brakes at low speeds. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, Vol. 215, Issue 5, 2001, p. 1245-1256.
-
Wang G. Y. Friction and testing of rubbers. Special Purpose Rubber Products, Vol. 21, Issue 3, 2000, p. 55-62.
-
Simpson Ibrahim Nonlinear friction-induced vibration in water-lubricated bearings. Journal of Vibration and Control, Vol. 2, 1996, p. 87-113.
-
Peng Engao, Liu Zhenglin, Tian Yuzhong, et al. Experimental study on friction-induced vibration of water-lubricated rubber stern bearing at low speed. International Conference on Frontiers of Manufacturing and Design Science, Applied Mechanics and Materials, Vol. 44, Issue 47, 2010, p. 409-413.
-
Tian Y. Z., Liu Z. L., Jin Y., et al. Mechanism analysis of squeal of water lubrication stern tube rubber bearing based on experimental study. Journal of Wuhan University of Technology, Vol. 1, 2011, p. 130-133.
-
Ryzhik B. Friction-induced vibrations of squeal type due to transverse contraction in a flexible disk. Journal of Sound and Vibration, Vol. 326, Issues 3-5, 2009, p. 623-632.
-
Mihajlović N. Torsional and Lateral Vibrations in Flexible Rotor Systems with Friction. Technische Universiteit Eindhoven, Aachen, 2005.
-
Li L. P., Zhou X. Y., Jin F. H. Influence of unbalance distribution on frictional vibration behavior of flexible rotors. Power Engineering, Vol. 25, Issue 6, 2005, p. 757-761.
-
Che K. K., Zhang Z. G., Zhang Z. Y., et al. Distributed-friction induced vibration in shafting system. Journal of Vibration and Shock, Vol. 20, 2014, p. 99-104.
-
Cheng F., Zhang Z. G., Zhang Z. Y., et al. Study on the self-excited oscillation of a propeller-shaft system under friction excitation. Noise and Vibration Control, Vol. 35, Issue 3, 2015, p. 117-120.
-
Zhang Z. G., Zhang Z. Y., Cheng F., et al. Research on the coupling between torsional and lateral vibrations in propeller-shaft system with friction. Journal of Mechanical Engineering, Vol. 49, Issue 6, 2013, p. 74-80.
-
Yang Ch Ch, Long X. H., Chen Y. Study on friction vibration of shaft-hull coupled system. Noise and Vibration Control, Vol. 34, Issue 5, 2014, p. 10-15.
-
Xiong Ch X., Xie J. R. A friction plane model for the research on self-excited vibration mechanism of Journal and Bearing. 14th Symposium on Underwater Noise, Chong Qing, 2013, p. 267-276.
-
Brake M. R. Frictional vibration transmission from a laterally moving surface to a traveling beam. Journal of Sound and Vibration, Vol. 310, Issue 3, 2008, p. 663-675.
-
Krauter A. I. Generation of squeal/chatter in water-lubricated elastomeric bearings. Journal of Lubrication Technology, Vol. 103, 1981, p. 406-413.
-
Li Ch B. Friction vibration (II) relation between dynamic friction and sliding velocity. Lubrication Engineering, Vol. 6, 1983, p. 49-55.
-
Peng E. G. Research on Friction-induced Vibration of Marine Water-lubricated Rubber Stern Tube Bearing. Wuhan University of Technology, Wuhan, 2013, (in Chinese).
-
Qing H. L. Study on Tribological Problems in Water-lubricated Compound Rubber Stern Tube Bearing. Wuhan University of Technology, Wuhan, 2012, (in Chinese).
-
Jin Y., Liu Z. L., Tian Y. Z., et al. Vibration monitoring of ship stern bearing based on pulse system. Journal of Wuhan University of Technology, Vol. 6, 2010, p. 84-88.
Cited by
About this article
The authors give sincere thanks to the editors and the reviewers for their patient work and constructive suggestions. This work is supported by the State Key Program Grant of National Natural Science Foundation of China (No. 51579198).
