Abstract
We discuss advantages and limitations of the harmonic balance method and the locus of a perturbed relay system (LPRS) method in the problem of finding periodic oscillations. In this paper we present the results of using harmonic balance method and LPRS method while investigating a 3rd order dynamic system in Lurie form. In this system a symmetric periodic oscillation is found, while other two asymmetric periodic motions are not found using both methods.
1. Introduction
The necessity of studying stability and limiting dynamical regimes (attractors) arises in classical theoretical and applied problems. In [1] the classification of oscillations as being hidden or self-excited was proposed: self-excited oscillations can be visualized numerically by a trajectory starting from a point in a neighborhood of unstable equilibrium. In contrast, the basin of attraction for a hidden oscillation is not connected with equilibria and, it is necessary to develop special analytical and numerical methods to find initial points for their visualization. For nonlinear systems with a unique equilibrium and bounded solutions, the question that arises is how to find a class of systems for which the condition of the impossibility of generation of self-excited oscillations implies the absence of hidden oscillations.
Among engineers, one of the most widely used methods for searching and analyzing oscillations in nonlinear control systems is the harmonic balance method. It was developed in the 1920-1930s in the works of van der Pol [2] and Krylov and Bogolyubov [3] and later developed in the works of their followers (see [4-6]). It is known [1] that the harmonic balance method is an approximate method for determining the frequency and amplitude of periodic solutions. Moreover, the harmonic balance method may not predict hidden periodic oscillations [1].
The latter is true for the locus of a perturbed relay systems approach (LPRS method), that was developed in [7, 8] for Lurie systems with relay nonlinearities, despite the fact that the LPRS method makes it possible in many cases to predict oscillations not discoverable by the harmonic balance method.
In this article, using the example of known dynamical system with coexisting self-excited periodic oscillations, we will show that these methods may not reveal self-excited oscillations.
2. Oscillations in relay systems
Consider the following system with one scalar relay nonlinearity in the Lurie form:
where is a state vector, , , , are matrices, all quantities are real. We consider the solution of system Eq. (1) in the Filippov sense [9].
2.1. Harmonic balance method
The classical harmonic balance method (e.g., see [10]) for system Eq. (1) computes a periodic oscillation in the following way: introduce a linearization coefficient so that matrix has purely imaginary eigenvalues , with the rest of its eigenvalues having negative real parts. Values of and can be found from equations:
where is the transfer function of system Eq. (1).
Finally, the amplitude can be found from the following harmonic balance equation:
Solving equation Eq. (3), we get:
2.2. LPRS method
Consider another method of analysis of periodic motions in relay feedback systems. The locus of a perturbed relay system (LPRS) method [7, 8] can be considered as a further development of Tsypkin’s ideas [11] on exact analysis of discontinuous systems. The basic concept of the method is as follows.
For system Eq. (1), following [8], we define a function which contains information on the frequency and amplitude of periodic oscillations. In this paper we apply a matrix state-space description approach to construct LPRS function for system Eq. (1):
Suppose we have computed the LPRS of a given system. Then there is a finite number of points of intersection of the LPRS and the horizontal axis. The following equation defines a frequency of a possible symmetric periodic solution of system Eq. (1):
Therefore, an actual periodic motion can be found only among these candidate points. Note that formula Eq. (6) is a necessary condition for the existence of the frequency of symmetric periodic motion in the system (the actual existence of a periodic motion depends on a number of other factors [8]).
3. Example: Atherton’s system
Consider a relay control system in Lurie form, introduced by D. Atherton in [12], with the following matrices:
where is a parameter.
The linear part of system Eq. (7) is defined by the transfer function:
and the stationary set is as follows:
From Eq. (2) we get value of :
and from:
we get
Next, from Eq. (4) we get value of amplitude :
For the value 1.2 we find frequency of a periodic solution as 2.75681. Now using formula Eq. (5) we build LPRS for system Eq. (7) (see Fig. 1).
Fig. 1The LPRS for system Eq. (7) for d = 1.2 and ω∈ [0.5, 10]
![The LPRS for system Eq. (7) for d = 1.2 and ω∈ [0.5, 10]](https://static-01.extrica.com/articles/20817/20817-img1.jpg)
Solving equation Eq. (6) using MATLAB function “vpasolve()” with a given tolerance 10-8, we find frequency of periodic solution as 2.739991399. Initial data this periodic solution is given in Table 1.
We can examine orbital stability of the oscillations using the following approach proposed in [13] and generalized for the linear parts containing delays and integrators in [8]. It is formulated as the following theorem:
Theorem 1. Periodic motions in system Eq. (1) are locally orbitally asymptotically stable if and only if all eigenvalues of the matrix:
where is the period of the oscillations, is the value of the velocity matrix at the time of the relay switch, in the periodic motion, , have magnitudes less than one.
For system Eq. (7) the corresponding eigenvalues are 1.457, 0.279, 0. Since one of eigenvalues has magnitude greater than 1, the motion is not orbitally stable. Therefore, a symmetric periodic solution exists but it is orbitally unstable and cannot reveal itself as an oscillation.
3.1. Numerical modeling
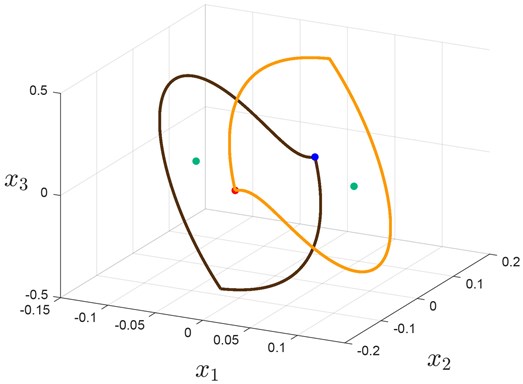
Using special computational package [14] and initial data from Table 2 we can visualize two self-excited (with respect to rest segment) asymmetric periodic solutions (see Fig. 2), that cannot be found using harmonic balance method and LPRS method.
Table 1Parameters of two asymmetric solutions of system Eq. (7)
2.608029064355592 | |
2.409169971705080 | |
0.296489410929823 |
Table 2Initial data of two asymmetric solutions of system Eq. (7)
0.000000000312706 | |
0.110095383325227 | |
0.037742341170832 |
Fig. 2Trajectories with initial data from Table 3
4. Conclusions
In this paper it is shown that the harmonic balance method and the LPRS method may not predict the existence of all self-excited oscillations. A symmetric periodic solution exists but it is orbitally unstable and cannot reveal itself as an oscillation. Although the LPRS does not detect hidden and self-excited asymmetric oscillations, it would be possible to develop a certain extension to the LPRS method to solve these problems.
References
-
Leonov G. A., Kuznetsov N. V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert- Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractors in Chua circuits. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering, Vol. 23, 2013, p. 1330002.
-
Van Der Pol B. On relaxation-oscillations. Philosophical Magazine and Journal of Science, Vol. 7, Issue 2, 1926, p. 978-992.
-
Krylov N. M., Bogolyubov N. N. Introduction to Nonlinear Mechanics. Princeton University Press, 1947, (in Russian).
-
Bulgakov B. V. Self-excited oscillations of control systems. Prikladnaya Matematika and Mekhanika, Vol. 7, Issue 2, 1943, p. 97-108, (in Russian).
-
Goldfarb L. S. Certain nonlinearities in control systems. Automatica and Telemekhanika, Vol. 8, Issue 5, 1947, p. 349-383, (in Russian).
-
Massera J. L. Contributions to stability theory. Annals of Mathematics, Vol. 64, 1956, p. 182-206.
-
Boiko I. M. Oscillations and transfer properties of relay servo systems – the locus of a perturbed relay system approach. Automatica, Vol. 41, 2005, p. 677-683.
-
Boiko I. Discontinuous Control Systems: Frequency-Domain Analysis and Design. Springer London, 2008.
-
Filippov A. F. Differential Equations with Discontinuous Right-Hand Sides. Kluwer, Dordrecht, 1988.
-
Khalil H. K. Nonlinear Systems. Prentice Hall, 2002.
-
Tsypkin Ya.Z. Relay Control Systems. University Press, Cambridge, 1984.
-
Atherton D. P. Correspondence: analytical determination of limit cycles for a class of third-order non-linear system. International Journal of Control, Vol. 21, Issue 6, 1975, p. 1021-1023.
-
Astrom K. J., et al. Adaptive Control, Filtering and Signal Processing. The IMA Volumes in Mathematics and its Applications, Vol. 74, 1995.
-
Piiroinen P. T., Kuznetsov Yu A. An event-driven method to simulate Filippov systems with accurate computing of sliding motions. ACM Transactions on Mathematical Software (TOMS), Vol. 34, Issue 3, 2008, p. 13.
About this article
This work was supported by the Russian Science Foundation 19-41-02002.
