Abstract
The vibration signal monitoring that is being generated by a rotor supported by a rolling element bearing is becoming important to define reliability of rotary machine. It is most prudent and useful method for bearing fault detection. Recently, there has been a lot of research on rolling element bearings fault. The kurtosis is most vital parameter to find inner race fault and outer race fault. It is enhanced by a proper selection of variable frame sizes and decompositions levels using wavelet based multi-scale principal component analysis (WMSPCA). It is observed that the kurtosis changes significantly as compared to the actual kurtosis of the un-decomposed faulty signals by proper selection of frame size and decompositions level.
1. Introduction
The rolling element bearings are one of the most important and frequently used components in vast majority of rotating machines. The breaking down of these bearings can result in machinery breakdown and can cause significant time and economic loss. Rolling element bearings may contain manufacturing errors or mounting defects and in many cases, damage may occur due to working conditions, such errors can cause noise, vibration and even whole system failure.
One of the important issues with these kinds of bearings is the reduction of noise and vibrations that originates from them. Even the geometrically perfect bearings produce vibrations while running. This is an inherent feature of these types of bearings and this happens because there are a limited number of balls that bear the external load. The other possible sources of vibrations can be unbalanced rotor force, distributed and localized defects of the rolling element bearing. The Vibration signal analysis is the most prudent and useful method for bearing fault detection. The signals emanating from the bearing are basically nonlinear and non-stationary. The signal is analyzed by statistical parameter and modeled by probability distribution functions (pdf). The shape of the distribution is used to identify the severity of fault [1]. The Kurtosis depends on the type of distribution function i.e. Gaussian, Laplacian, Weibull etc. and its biasing [2-4]. The analysis of pdf is done by Kolmogorov Smirnov test (K-S test), Anderson Darlington test (A-D test), Chi- Square test, Shapiro-Wilk normality test etc. [5, 6]. The probability density function changes as the fault changes, the graphical, as well as the analytical method, can give the approximate detail about the closeness of the data to a particular distribution. The distribution function and the fourth order moment i.e. kurtosis has a significant impact in differentiating the state of the bearing. The kurtosis can be used to decode the fault in time domain, frequency domain, and time-frequency domain [7, 8]. Westfall etc. correlate it with fault detection [9, 10]. The influence of different mathematical operators can change the statistical properties of the signals [11]. The change in the mathematical operator can enhance or dilute the information content present in the signals. Few mathematical operators that can be included to demodulate the signals are the envelope detection and cepstrum analysis technique. The Hilbert transform is used to demodulate the modulated signals [12, 13]. The side band component is reduced by logarithm function in frequency domain [14].
There are ample of signal processing methods available for fault diagnosis of the bearing. The extraction of information depends on the statistical feature or the distribution and basis function used to cipher information present in the signal. In past few years, different signal processing techniques have been developed to extract information from the noisy signals. The statistical approach of evaluating the signals can be best achieved using non-stationary signal processing methods. The non-stationary signal in the bearing can be extracted using different flavor of Wavelet transforms (WT) [15-17], EMD (empirical mode decomposition) [18], VMD (variational mode decompositions) [19], Wigner-Ville distributions (WVD) etc. [20]. None of these methods can extract information in standalone. All are interdependent to extract faithful information's present in the signal i.e. it needs a fusion of some of these algorithms along with the statistical feature extraction techniques. But, for our analysis wavelets are used as it can approximate the actual signal using the scaling and time shifting properties. The fusion of different techniques like PCA along with wavelet transforms can be a valuable asset in the extraction of bearing fault. These PCA-based process monitoring methods employ wavelet analysis to transform time-domain signals in the time-frequency domain so significant events can be recombined to obtain a PCA model for all scales together [21, 22]. WMSPCA uses the multi-scale dynamic property of the wavelet and PCA to de-correlate the cross-correlated signals simultaneously.
This paper is organized as follows: Section 2 describes the proposed algorithm. Section 3 describes the experimental approach used to acquire signals. Section 4 discusses the results and the improvement in 4th order statistical moments for the inner race defect and outer race defect. Section 5 concludes the paper.
2. The proposed algorithm
The proposed algorithm is applied to faulty signals for different frame length and wavelet decomposition levels and their effect on kurtosis is studied. The process adopted in this algorithm is shown in Fig. 1.
Fig. 1Decomposition of bearing fault signal using WMSPCA
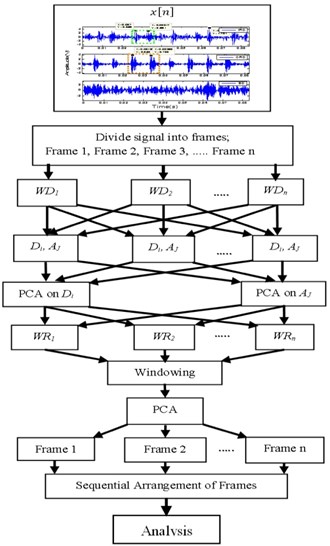
The detail of signal analysis stages are as follows:
a) These signals are divided into frames ranging from 2 to 10. The Wavelet decomposition is applied to the frames to segregate the low and high-frequency signals. Wavelet is applied to de-correlate the auto correlated signals.
b) PCA is applied to these signals to un-correlate the correlated signals.
c) The uncorrelated data matrixes are further decomposed using same wavelet coefficient to construct the signals.
d) Finally, the thresholding technique using Kaiser Rule is applied to the reconstructed signal i.e. signal above the mean of the Eigen values is retained to analyze the behavior [23]. Again, PCA is used to produce new uncorrelated frames from segmented frame. Finally, the frames are sequentially arranged to construct the signal and the kurtosis is calculated.
e) All the above processes are repeated for different frame sizes and different wavelet decomposition levels.
3. Experimental approach
The experimental setup and vibration signals are taken from the Case Western Reserve University bearing data center is shown in Fig. 2. The experiment test bench consists of a 2 hp motor, a torque transducer/encoder, a dynamometer and a 6205-2RS deep groove ball bearing. In this experimentation different faults are created in inner race, outer race and on the ball using electro-discharge machining (EDM). Drive end vibration data of the bearing are collected using accelerometers mounted on a magnetic base at 6 o’clock positions. The vibration signals are collected at a sampling rate of 12000 samples per sec using a 16 channel data acquisition card. (http://data-acoustics.com/measurements/bearing-faults/bearing-5/) Table 1 represents the bearing configuration.
Table 1Ball bearing specifications
Bearing type | Pitch diameter (in) | Rolling element diameter (in) | Number of rolling elements |
6205-2RS JEM SKF (DGBB) | 1.537 | 0.3125 | 9 |
Fig. 2Experimental set up with sensors (CWRU)

4. Results and discussion
To understand and examine the influence of different wavelet transforms and its impact on variable correlated sample data to calculate the kurtosis, the WMSPCA is used to improve the kurtosis value to enhance the faulty feature of the bearing over the noise. The fault signal is acquired at a sampling rate of 12000 samples/sec and the observed sample points are 24000. The samples are divided into frames i.e. ranging from two to ten frames successively. Then WMSPCA is applied on the frames for different wavelet decomposition level as shown in Fig. 1. Finally, the kurtosis for different faults is analyzed.
It is observed the kurtosis has different values for the different level of decompositions and frame sizes. Fig. 3(a) shows the different values of kurtosis obtained for IRD using Daubechies. The kurtosis is almost consistent for the fifth frame with a variation in the decomposition. It is inferred due to variation in the frame numbers and decomposition levels, the pattern followed by the kurtosis changes. It signifies the sample size; mother wavelet scaling and shifting plays a crucial role in the extraction of signal from the noise.
It is observed from Fig. 3(b) that the kurtosis increases when the numbers of frames are two. This analysis shows that the kurtosis is rather unsmooth for different decomposition levels for the ORD. For certain Db and frame ( 2 and 10) the kurtosis reaches to its maximum of 11.432. For analysis, the reference thresholds are 5.38 and 7.557 for the kurtoses respectively for IRD, ORD. The performance of Symlet for IRD and ORD are shown in Fig. 4. It is observed the performance of Symlet matches to that of Daubechies at certain instances, if not true for all the frame numbers. The kurtosis decreases from the actual reference if the number of frames and decomposition levels are not properly chosen. The analysis can be precipitate to a conclusion that the behavior of the two different wavelets converges at certain decomposition levels and frame sizes. Finally, it is observed, the WMSPCA significantly improves the kurtosis using iterative decomposition and framing schemes. These decomposition methods help in improving the kurtosis i.e. by shifting the distribution closer to the mean rather towards the tail end. WMSPCA is showing promising results in kurtosis extraction and is almost independent of the choice of the wavelets.
Fig. 3Kurtosis for different frames and wavelets (Daubechies): a) IRD, b) ORD
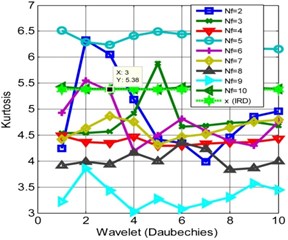
a)
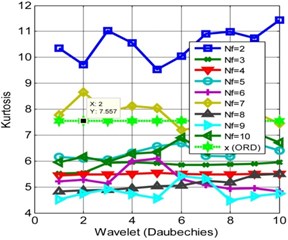
b)
Fig. 4Kurtosis for different frames and wavelets (Symlet): a) IRD, b) ORD
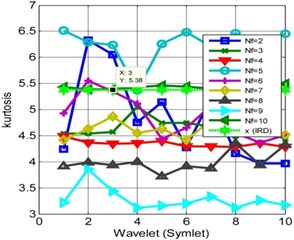
a)
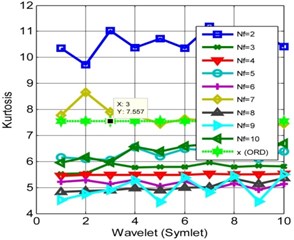
b)
5. Conclusions
It is observed that the kurtoses of the signals are improved by WMSPCA, number of frames and decomposition levels. The Kurtoses increases with increase in fault dimension and reflects the closeness of particular fault to the sensor. The kurtosis improvement in IRD and ORD indicate the decrease in noise when the actual kurtosis obtained without it is considered as a reference. These analyses also clarify that the kurtosis based performance analysis improves only for the certain value of the frame and the decompositions levels. It is also observed that the Symlet and Daubechies performances are almost same when the kurtosis is high. The noise performance is improved irrespective to wavelet.
References
-
Walck C. Hand-Book on Statistical Distributions for Experimentalists. University of Stockholm, 2007.
-
Rosser G., Fletcher A. G., Maini P. K., Baker R. E. The effect of sampling rate on observed statistics in a correlated random walk. Journal of Royal Society of Interface, Vol. 10, 2013, https://doi.org/10.1098/rsif.2013.0273.
-
Schwede R. L., Cirpka O. A., Nowak W., Neuweiler I. Impact of sampling volume on the probability density function of steady state concentration. Water Resource Research, Vol. 44, 2008, p. W12433.
-
Decarlo L. T. On the meaning and use of kurtosis. Psychological Methods, Vol. 2, Issue 3, 1997, p. 292-307.
-
Broom M., Nouvellet P., Bacon J. P., Waxman D. Parameter-free testing of the shape of a probability distribution. Biosystems, Vol. 90, Issue 2, 2007, p. 509-515.
-
Park H. M. Univariate analysis and normality test using SAS. The Trustees of Indiana University, 2006.
-
Randall R. B., Antoni J. Rolling element bearing diagnostics-A tutorial. Mechanical Systems and Signal Processing, Vol. 25, Issue 2, 2011, p. 485-520.
-
Kang M., Kim J., Wills L. M., Member S., Kim J. Time-varying and multiresolution envelope analysis and discriminative feature analysis for bearing fault diagnosis. IEEE Transactions on Industrial Electronics, Vol. 62, Issue 12, 2015, p. 7749-7761.
-
Westfall P. H. Kurtosis as peakedness, 1905-2014. R.I.P. Journal of the American Statistical Association, Vol. 68, Issue 3, 2014, p. 191-195.
-
Jahagirdar A. C., Mohanty S., Gupta K. K. Study of noise effect on bearing vibration signal based on statistical parameters. Vibroengineering Procedia, Vol. 21, 2018, p. 26-31.
-
Balakrishnan A. V. Effect of linear and nonlinear signal processing on signal statistics. Radio Science, Vol. 68, Issue 9, 1964, p. 953-965.
-
Klingspor M. Hilbert Transform: Mathematical Theory and Applications to Signal Processing. Linköpings Universitet, Linköping, 2015.
-
Johansson M. The Hilbert Transform. Master Thesis, Vaaxjao University, 1999.
-
Randall R. B. A history of cepstrum analysis and its application to mechanical problems. The International Conference Surveillance 7, 2013.
-
Rafiee J., Rafiee M. A., Tse P. W. Application of mother wavelet functions for automatic gear and bearing fault diagnosis. Expert Systems with Applications, Vol. 37, 2010, p. 4568-4579.
-
Boudiaf A., Moussaoui A., Dahane A. A comparative study of various methods of bearing faults diagnosis using the Case Western Reserve University data. Journal of Failure Analysis and Prevention, Vol. 16, 2016, p. 271-284.
-
Govandhan T. Identification of faults through wavelet transform vis-a-vis fast Fourier transform of noisy vibration signals emanated from defective rolling element bearings. Journal of Failure Analysis and Prevention, Vol. 9, 2014, p. 130-141.
-
Ahn J., Kwak D., Koh B. Fault detection of a roller-bearing system through the EMD of a wavelet denoised signal. Journal of Sensors, Vol. 14, 2014, p. 15022-15038.
-
Mohanty S., Gupta K. K., Raju K. S. Bearing fault analysis using variational mode decomposition. Journal of Instrumentaion Technology, Vol. 4, 2014, p. 20-27.
-
Feng Z., Liang M., Chu F. Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples. Journal of Mechanical Systems and Signal Processing, Vol. 38, 2013, p. 165-205.
-
Mohanty S., Gupta K. K., Raju K. S. Multi-channel vibro-acoustic fault analysis of ball bearing using wavelet based multi-scale principal component analysis. Proceeding of 21st National Conference on Communication (NCC), 2015.
-
Bakshi B. R. Multiscale PCA with applications to multivariate statistical process monitoring. AICHE Journal, Vol. 44, 1998, p. 1596-1610.
-
Jackson D. A. Stopping rules in principal component analysis: a comparison of heuristical and statistical approaches. Journal of Ecology, Vol. 78, 1993, p. 2204-2214.
