Abstract
In this paper, an improved BP neural network algorithm is applied to the fault diagnosis of aircraft fuel system. The simulation results show that the algorithm has the characteristics of fast diagnosis speed and low misdiagnosis rate, and lays a foundation for the development of aircraft fuel fault diagnosis expert system based on neural network.
Highlights
- The improved BP neural network is applied to the fault diagnosis of B737 aircraft fuel system
- The typical BP neural network algorithm has the characteristic of fixed step size, which is not conducive to fast convergence in some cases.
- The improved BP neural network algorithm has faster diagnosis speed, more accurate output results and lower misdiagnosis rate.
- By improving and optimizing the typical BP neural network, the fault diagnosis rate of B737 aircraft fuel system can be improved and perfected.
1. Introduction
As a popular fault diagnosis method, expert system diagnosis can effectively deal with many kinds of fault diagnosis problems that have appeared in the past. However, for the first new fault, because there is no corresponding diagnostic knowledge in the rule base of expert system, the expert system cannot deal with the fault, which also limits its further development in the field of application [1].
BP neural network originated in 1986 and was first proposed by McCelland and Rumelhart et al. It belongs to a special multi-layer feedforward network trained by error back propagation algorithm. It can solve some complex problems and develop a series of links, such as speculation, Association and memory, so that the fault diagnosis rate can be improved. Therefore, this method is very suitable for the fault diagnosis of modern large aircraft [2]. In BP neural network, its network structure will directly affect the generalization ability and computational complexity of learning algorithm. Fewer nodes will lead to inadequate training, and too many nodes may over-fit training data. So, one of the hot issues in the current research of neural network is how to determine the optimal network structure [3].
In this paper, the improved BP neural network is applied to the fault diagnosis of B737 aircraft fuel system. By improving and optimizing the typical BP neural network, the fault diagnosis rate of B737 aircraft fuel system can be improved and perfected.
2. An improved BP neural network algorithm
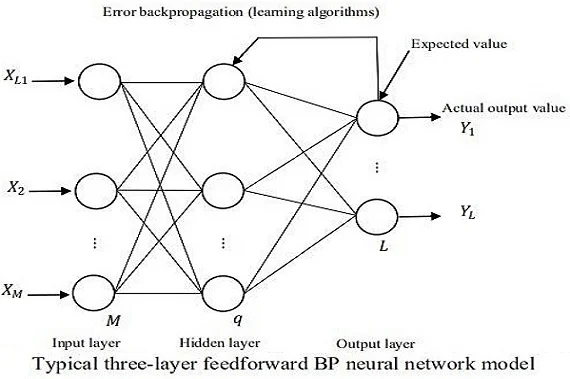
A typical BP neural network has three core neurons: input layer, hidden layer and output layer. Fig. 1. is a typical three-layer feedforward BP neural network model [4].
According to literature [4], in the three-layer feedforward BP neural network model, the difference between the field expert knowledge and the simulation results of BP neural network algorithm can be used to obtain an error, and then the corresponding output decision can be obtained by adjusting the internal parameters of BP neural network.
Assuming that a typical training sample of BP neural network is , in the input layer, in the hidden layer, in the output layer, and are the connection weights between the input layer and the hidden layer, and are the node thresholds between the hidden layer and the output layer respectively, is the learning efficiency (between 0 and 1). Its network learning algorithm is as follows [5].
1) Initialization: It means that all weights and thresholds are set to initial values.
2) Provide training samples : representing the known input vector and the expected target output vector ;
3) Calculate the actual output.
Fig. 1Typical three-layer feedforward BP neural network model
Cryptocortical neuron output:
Output layer neurons output:
4) Calculate the error between the expected value and the actual output value:
In the formula, – represents the logarithm of the sample pattern, – represents the expected output value of the network, – represents the actual network output.
5) Correction of the weights of neurons in the output layer:
6) Modification of the weight coefficients of the hidden layer neurons:
If the error between the expected output and the actual output is , which satisfies the relevant requirements of the system, the algorithm will terminate. On the contrary, it will return to step 2 for repeated calculation until the error E meets the requirements. However, because the typical BP neural network algorithm has the characteristic of fixed step size, which is not conducive to fast convergence in some cases, it is necessary to improve and optimize the BP neural network algorithm [6].
Therefore, in the fault diagnosis of B737 aircraft fuel system, the following two important improvements are made in the training steps of BP neural network, and the network structure is optimized [7]:
The input training data is . When calculating the output value , the weights between the hidden layer neurons and the output neurons are adjusted:
Among them:
The learning rate is , the coefficient of momentum term is , the output of at the iteration time of neurons in the hidden layer is , the output error signal between the expected output value and the output value of at the iteration time of neurons in the hidden layer is:
The improved scheme adopts a variable step-size approach and incorporates the weighted fading factor , then Eq. (2) is transformed into:
Among them:
Among them, and initial subtraction factor are taken as design parameters, and usually chooses 0.99 and usually chooses 0.95.
(2) The weights between the neurons in the input layer and the neurons in the hidden layer were adjusted:
can be calculated by the following formula:
Among them, is the input variable of .
Similarly, after the improved BP neural network algorithm, Eq. (6) becomes:
The learning rate is , which determines the step size of gradient descent method. Because if the value is higher than the standard value, the weight will oscillate greatly; otherwise, if the value is lower than the standard value, the convergence will become too slow. According to the relevant theoretical research, the number of neurons in the hidden layer and the optimal learning rate are inversely proportional. For all the neurons, the learning rate is the same in general. In many practical applications, the value of the learning rate is usually 0.35. The momentum coefficient represents the dependence of the change value of the weight on the change value of the previous moment, and its value is usually 0.7.
3. Application of improved BP algorithm in fault diagnosis of B737 aircraft fuel system
In the fuel system of B737 aircraft, the fuel tank is divided into No. 1 (left wing), No. 2 (right wing) and central fuel tank. The three fuel tanks are relatively independent. The No. 1 and No. 2 fuel tanks are located in the left- and right-wing structures, which are symmetrically distributed. They are divided into two groups. There are four fuel tanks on each wing of the aircraft, namely, fuel consumption tank, pre-fuel consumption tank, auxiliary fuel tank and backup fuel tank. In order to facilitate further research, the improved BP neural network algorithm is adopted, and the fault analysis of a single group of pre-consumption tank oil delivery system is carried out.
The system can obtain a total of 6 measurement parameters, which are: pre-consumption tank oil level (); pre-consumption tank one-way valve outlet pressure (); pre-consumption tank oil pump outlet pressure (); pre-consumption tank oil pump current (); consumption tank oil level (); pipeline pressure (). There are four common faults in the pre-consumption tank oil delivery system, which are one-way valve fault (), pre-consumption tank leakage (), pump failure (), pipeline leakage (). For example, the typical manifestation of one-way valve failure is that the pressurized air cannot enter the predicted fuel consumption tank of the wing, thus losing the power of oil transmission, which can be judged by the abnormal phenomena of oil transmission in the predicted fuel consumption tank; the typical manifestation of oil pump failure is that the aircraft can only rely on the gravity of fuel, and the oil transmission will be slow, which can be judged by the abnormal phenomena of oil exhaustion signal lamp operation.
In the improved BP neural network, the input node selection value is 6, the hidden layer node selection value is 6, and the output node selection value is 4. The relationship between fault causes and symptoms is regarded as the learning object of the neural network, and then the measured value is used as the input parameter, and the improved BP neural network is used for fault diagnosis. According to the existing fault phenomena and modes of the system, to find a solution strategy for this fault mode, and then form a pair of samples as training samples, and send them to the improved BP neural network for adjustment. When the input is -, the values of –1, 0 and 1 are lower, normal and higher, respectively. If the input neuron is related to a fault in the system, the output neuron representing the fault will be defined as “1” and vice versa, as “0” [8]. The training parameters selected by the improved BP neural network are shown in Table 1.
Table 1Training parameters selected by improved BP neural network
Parameter name | Selected value | Parameter name | Selected value |
0.2 | The node number of input layer | 6 | |
0.7 | The node number of output layer | 4 | |
0.95 | The node number of hidden layer | 6 | |
0.99 | – | – |
The improved BP neural network algorithm is used for scheme selection, and the improved BP neural network is trained with the help of the function operation of the neural network toolbox in MATLAB software.
Firstly, the fault sample matrix (including input and output samples) of the pre-consumption tank oil delivery system is constructed, as shown in Table 2.
Secondly, the improved BP neural network is initialized with “initff” function, and the number of nodes and activation function of each layer of neural network are obtained. Its specific function form is as follows:
, are expressed as the weights and thresholds of each layer of neurons, is expressed as input vector;
Thirdly, the target error, number of cycles and learning rate of network training are set to 0.2, and “trainbp” function is used to train the improved BP neural network.
Fourthly, the trained BP neural network is simulated by using “simuff” function. The target error, the number of cycles and the learning rate remain unchanged. The results are shown in Table 3.
Table 2Fault diagnosis result of B737 aircraft pre-consumption tank fuel delivery system
Input | Output (%) | Fault type | ||||||||
1 | 0 | 0 | 1 | –1 | 0 | 0 | 0 | 100 | 0 | |
1 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 100 | 0 | |
1 | 0 | 1 | 0 | –1 | 0 | 0 | 0 | 100 | 0 | |
1 | 0 | –1 | 0 | –1 | 0 | 0 | 0 | 100 | 0 | |
1 | –1 | 0 | 0 | –1 | 0 | 100 | 0 | 0 | 0 | |
1 | 1 | 0 | 0 | –1 | 0 | 100 | 0 | 0 | 0 | |
1 | 0 | 0 | 0 | –1 | 0 | 0 | 100 | 0 | 0 | |
1 | –1 | 0 | 1 | 0 | 0 | 100 | 0 | 100 | 0 | |
1 | –1 | –1 | 0 | 0 | 0 | 100 | 0 | 100 | 0 | |
1 | –1 | –1 | 0 | 0 | –1 | 0 | 0 | 100 | 100 | |
1 | 0 | 0 | 0 | –1 | –1 | 0 | 100 | 0 | 100 | |
Table 3Fault diagnosis result of B737 aircraft pre-consumption tank fuel delivery system
Input | Output (%) | Fault type | ||||||||
0 | 0 | 92.0 | 0 | |||||||
1 | 0 | 0 | 1 | –1 | 0 | 0 | 0 | 93.0 | 0 | |
1 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 93.0 | 0 | |
1 | 0 | 1 | 0 | –1 | 0 | 0 | 0 | 96.0 | 0 | |
1 | 0 | –1 | 0 | –1 | 0 | 95.0 | 0 | 0 | 0 | |
1 | –1 | 0 | 0 | –1 | 0 | 97.0 | 0 | 0 | 0 | |
1 | 1 | 0 | 0 | –1 | 0 | 0 | 95.0 | 0 | 0 | |
1 | 0 | 0 | 0 | –1 | 0 | 92.0 | 0 | 98.0 | 0 | |
1 | –1 | 0 | 1 | 0 | 0 | 96.0 | 0 | 95.0 | 0 | |
1 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 95.0 | 99.0 | |
1 | –1 | –1 | 0 | 0 | –1 | 0 | 98.0 | 0 | 99.0 | |
According to the above fault diagnosis results, for the information samples that have appeared before, the expected results are in good agreement with the values output by the improved BP neural network, which fully verifies that the BP neural network can complete the fault diagnosis of B737 aircraft fuel system. If more new fault training samples are added to the original fault samples of the network, the output results of the improved BP neural network will be more accurate and efficient.
4. Conclusions
Through the fault diagnosis results of B737 aircraft fuel system, it is verified that the improved BP neural network algorithm has faster diagnosis speed, more accurate output results and lower misdiagnosis rate, which makes up for the shortcomings of expert system diagnosis method. It also lays a solid foundation for the further organic combination of the two methods and the research of B737 aircraft fuel fault diagnosis expert system based on BP neural network, so as to facilitate the future. The algorithm can be successfully applied to the fault handling of B737 aircraft intelligent fuel management system.
References
-
Wan Peng Research and Implementation of Flight Control Ground Fault Diagnosis System Based on Symptom Analysis. University of Electronic Science and Technology, Chengdu, 2018.
-
Ling Yiqin Research on Fault Diagnosis Technology of Aircraft System Based on Fault Propagation Mechanism and Petri Net. Nanjing University of Aeronautics and Astronautics, Nanjing, 2017.
-
Hao Yichuan Research on Fault Diagnosis Method of Aircraft Electronic System Based on Rough Set and Neural Network. China Civil Aviation University, Tianjin, 2015.
-
Deng Zheng Research on Aircraft Burst Fault Diagnosis Based on T-S Fuzzy Neural Network. China Civil Aviation University, Tianjin, 2014.
-
Dai Min, Zhu Jiaxiong, He Yuanhua Fault diagnosis of aircraft fuel system based on SOM algorithm and immune neural network. Computer Measurement and Control, Vol. 22, Issue 11, 2014, p. 3483-3486.
-
Diao Hai-Fei Research of Comprehensive Maintenance Task Optimization Method Based on Similar Models Data. Nanjing University of Aeronautics and Astronautics, Nanjing, 2014.
-
Zuo Hong-Fu, Cai Jing, Wu Hao Aviation Maintenance Engineering. Science Press, Beijing, 2011.
-
Wan Fengqin, Yan Jianguo, Shi Xiaoli, Yu Long Application of an improved BP neural network in fault diagnosis of aircraft fuel system. Computer Measurement and Control, Vol. 14, Issue 7, 2006, p. 867-871.
About this article
Project supported by National Natural Science Foundation of China, NO: 51605037; Binzhou University Scientific Research Fund Project, No. BZXYG1705; Binzhou University Double Service Project, No. BZXYSFW201813.
