Abstract
The inverse acoustic scattering model for crack diagnosis is described by Helmholtz problem within mathematic framework and investigated for the sake of scientific computing. Minimizing the misfit from given measurements leads to an optimality condition-based imaging function which is used for non-iterative identification of the center of an unknown crack put in a test domain. The numerical tests are presented for the cracks of T-junction shape and are carried out based on the Petrov-Galerkin generalized FEM using wavelets basis and level-sets. This shows high-precision identification result and stability to noisy data of the diagnosis, which is illustrated for sound-soft as well as moderately sound-hard cracks when varying the coefficient of surface impedance.
Highlights
- The inverse acoustic scattering problem is investigated for scientific computing of crack diagnosis
- Minimizing the misfit from given measurements leads to an optimality condition-based imaging
- Imaging function is used for non-iterative identification of the center of a crack put in test domain
- Numerical tests are based on Petrov-Galerkin GFEM and wavelet basis
- T-junction shaped cracks are sound-soft as well as sound-hard with moderate surface impedance
- High-precision identification result and stability to noisy data of the diagnosis are reported
1. Introduction
In this contribution, the Helmholtz problem describing scattering of homogeneous acoustic medium that contains the single defect described by a cluster of cracks like T-junctions and characterized by surface impedance (thus, inhomogeneous medium) is considered. The inverse acoustic scattering problem is aimed at crack diagnosis motivated by applications to non-destructive testing with acoustic, electromagnetic, and elastic waves in engineering sciences.
The classic approach to inverse scattering problems in the context of mathematical modeling was established based on the operator theory, which results in direct (non-iterative) solution methods such as factorization, sampling, enclosure, MUSIC-type algorithms, and alike. The classic analysis utilizes fundamental solutions and Green’s functions for respective boundary value problems. In comparison, iterative methods are mostly used for the reason of numerical computing of the solution.
Recently, the shape optimization approach to identification of small geometric objects was developed based on the concept of topological derivative (when relating inhomogeneous medium to the background homogeneous one). The corresponding asymptotic analysis realizes the methods of singular perturbations. For the optimization approach adapted to inverse scattering problems, see the author’s works [1] related to sound-soft and sound-hard obstacles, and [2] for diagnosis of inhomogeneities in the background medium. The first-order topological derivative specified for geometric objects with real-valued refractive index was found in [3], and the high-order topological expansions were derived in [4].
Following the shape optimization, the imaging function is determined by the incident background field and the known measurement. In [1] it was applied for identification of the center of impedance obstacles from boundary measurements, and in [2] for identification of the center of an inhomogeneity from the known far-field pattern. The latter work used an equivalent formulation of the scattering problem in the form of a weakly singular integral equation of Lippmann-Schwinger. The numerical tests were carried out in 2d and 3d and demonstrated high-precision of the identification result and its stability with respect to the a-posteriori errors due to discretization as well as noisy data.
In the current contribution we extend the optimality condition-based imaging technique and successfully apply numerical algorithm for diagnosis of cracks. For the variational theory of cracks, see [5].
2. Theory
The theoretical result is established in the following manner. A least square cost functional of the misfit from a given measurement is minimized. To define the set of feasible parameters we describe the unknown crack with the help of geometric variables of its shape, center, size, and surface impedance coefficient [0, ]. The weak variational formulation of the minimization problem with respect to these variables provides us with the zero-order necessary optimality condition, which is derivative-free. Further applying asymptotic arguments as the size tends to zero, for the sound-soft crack as the optimality condition with respect to the center was derived in [1, 2] as follows:
and the imaging function is defined for spatial points by the following imaginary part:
In Eq. (2) the complex-valued function yields the incident field determined in the background homogeneous medium with the wave number that satisfies the Helmholtz equation:
where stands for the gradient vector and for the Laplace operator. The other complex-valued function solves the adjoint Helmholtz problem:
for the measurement given at the observation boundary with the normal vector , and in Eq. (2) is its complex conjugate.
3. Methods
Motivated by the special need of highly accurate and stable interpolation for the variational solutions of the acoustic scattering problem, in [6] we developed the concept of Petrov-Galerkin enrichment by a finite element method (FEM). To reduce the discretization error, we enriched the space of test functions based on necessary optimality conditions for interpolation properties. Using a Petrov-Galerkin approach, we suggested low order interpolation polynomials for the trial space, and we enriched the test space with high order shape functions. Henceforth, the resulting Petrov-Galerkin enrichment (PGE) has low computational costs, but it improves significantly the accuracy of interpolation which is of the seventh order. In [6] justification of PGE was provided by local wavelets with vanishing moments based on the Gegenbauer polynomial approximation. Practical formulas were derived for calculation of the system matrix for the reference Helmholtz equation given over uniform meshes in 2d and 3d. In the current work we apply the PGE algorithm for computation of the Helmholtz problems Eqs. (4) and (7).
From Eqs. (1) and (2) it follows that the true center belongs to zero-level set of that is:
hence forces the numerical algorithm finding approximate center from multiple measurements , , … and zero-level sets , , … by the mean of intersection:
where associates the mesh size appeared in numerical computation of problem Eq. (4).
4. Results
We present our numerical tests over the uniform quadrilateral grid of size 2-7 in 2d implying the degrees of freedom DOF = 16641 in the computational domain (0, 1)(0, 1). The crack of T-junction shape and of size 0.0194 posed at the center (0.1467, 0.3750) is drawn in Fig. 1 and Fig. 2. The measurements and are synthesized by solving numerically the forward scattering problem for 1, 2:
where the incident field is prescribed by the plane wave:
in the scattering directions /8 and /4, and the wave number /2 fixed.
We distinguish the crack scattering by varying the surface impedance coefficient [0, ] in Eq. (7) thus approaching the sound-hard 0 and the sound-soft cases. The typical identification result of due to Eq. (6) for large is depicted in Fig. 1 as 1.
Fig. 1Identification of the center of crack when impedance α= 1 (approaching sound-soft case)
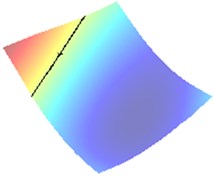
a) Wave direction /8
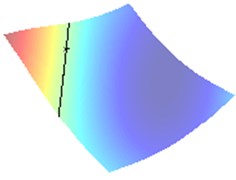
b) Wave direction /4

c) Zero level sets
In Fig. 2(a) and 2(b) respectively there are drawn the numerically computed imaging functions and . Its zero-level sets and are utilized numerically by the narrow band technique and form the straight lines crossing the crack. Both the zero-level sets are depicted together in the computational test domain in Fig. 2(c). Their intersection point is very close to the true center as can be verified in Table 1.
For comparison, the cross-point for small is presented in Fig. 2 as 0.01. This picture shows the error of approximation of caused by curving the zero-level sets.
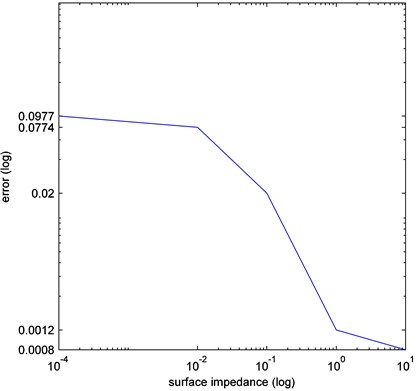
All the results of numerical tests are gathered together in Table 1 also quantifying the absolute error of the identification algorithm. In particular, in the last column we observe the relative error given with respect to the mesh-size . This fact clearly demonstrates that for moderate 1 the Euclidean distance between the centers and is significantly less than the mesh-size (in the range of 1-30 % of ), which definitively justifies the high-precision property of our algorithm.
Fig. 2Approximation of the center of crack when impedance α= 0.01 (approaching sound-hard case)
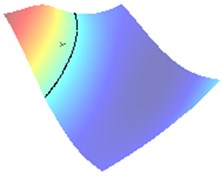
a) Wave direction /8
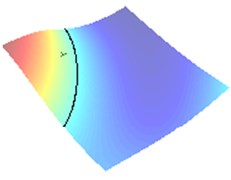
b) Wave direction /4
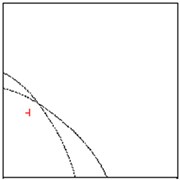
c) Zero level sets
Table 1Identification result of center x*= (0.1467, 0.3750)
Surface impedance | Approximate center | Absolute error | Error related to |
(0.1490, 0.3750) | 0.0023 | 0.2984 | |
1000 | (0.1489, 0.3750) | 0.0022 | 0.2798 |
100 | (0.1479, 0.3750) | 0.0012 | 0.1486 |
10 | (0.1459, 0.3750) | 0.0008 | 0.0975 |
1 | (0.1479, 0.3752) | 0.0012 | 0.1530 |
0.1 | (0.1592, 0.3906) | 0.0200 | 2.5589 |
0.01 | (0.2031, 0.4280) | 0.0774 | 9.9084 |
0.0001 | (0.2422, 0.4438) | 0.0977 | 12.5074 |
The error versus from Table 1 is also illustrated for convenience in the log-log plot in Fig. 1. This curve exhibits the bounded limit behavior as 0 and .
Fig. 3Identification error when varying impedance (sound-hard α= 0 and sound-soft α=∞)
5. Conclusions
Although the inverse acoustic scattering theory of Section 2 is derived rigorously when getting to the limit of the size and the surface impedance coefficient, the computer simulation ensures that the imaging function in Eq. (2) is still acceptable for moderate values of the parameters. This conclusion holds true also for the diagnosis of cracks treated here.
References
-
Kovtunenko V. A., Kunisch K. High precision identification of an object: optimality conditions based concept of imaging. SIAM Journal of Control and Optimization, Vol. 52, Issue 1, 2014, p. 773-796.
-
Cakoni F., Kovtunenko V. A. Topological optimality condition for the identification of the center of an inhomogeneity. Inverse Problems, Vol. 34, Issue 3, 2018, p. 035009.
-
Kovtunenko V. A. Two-parameter topological expansion of Helmholtz problems with inhomogeneity. Mathematical Analysis of Continuum Mechanics and Industrial Applications. Mathematics for Industry, Vol. 26, 2017, p. 51-81.
-
Kovtunenko V. A. High-order topological expansions for Helmholtz problems in 2d. Topological Optimization and Optimal Transport, Radon Series on Computational and Applied Mathematics, Vol. 17, 2017, p. 64-122.
-
Khludnev A. M., Kovtunenko V. A. Analysis of Cracks in Solids. WIT-Press, Southampton, Boston, 2000.
-
Kovtunenko V. A., Kunisch K. Revisiting generalized FEM: a Petrov-Galerkin enrichment based FEM interpolation for Helmholtz problem. Calcolo, Vol. 55, 2018, p. 38.
About this article
The author is supported by the Austrian Science Fund (FWF) Project P26147-N26: ‘Object Identification Problems: Numerical Analysis’ (PION) and the Austrian Academy of Sciences (OeAW), the RFBR and JSPS research Project 19-51-50004.
