Abstract
Preliminary, numerical analyses of a novel Structural Health Monitoring (SHM) technique are reported. Based on recent developments of new rotation rate (rotation velocity) sensing devices, it is proposed to use the rotational sensors to measure the rotational difference of structural members to indicate plastic hinge development at the early stage. Respective difference between rotations of two adjacent corner nodes during seismic excitation is used to indicate and possibly quantify plastic hinge formation during seismic response of a moment resisting frame. The preliminary numerical analysis leads to a positive conclusion for the application of the rotation rate sensors in ‘on-line’ monitoring of moment resisting frames subjected to strong, damaging seismic ground motions.
1. Introduction
After a rapid development in mechanical engineering and aeronautics, the SHM (Structural Health Monitoring) techniques are becoming more and more popular also in civil engineering. An important branch of SHM is vibration-based damage detection which is a very wide area of research [1]. Most of these methods are using small, diagnostic vibrations coming from ambient excitations or harmonic shakers usually to detect the damages after the damage occurred. There are however also methods aiming at “on-line” damage detection. They can be used to raise alarms immediately during the damaging vibrations or when the structure is overloaded in a different way (e.g. too much snow on a roof, heavy truck passage over a bridge etc.).
Fig. 1A moment resisting frame under seismic excitations with two rotational sensors placed at its corner (two little squares) to monitor plastic hinge development
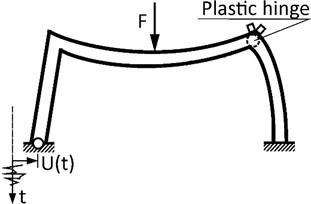
For obvious reasons the SHM techniques of vibration-based damage detection are primarily important in earthquake engineering applications where they can be used for intelligent structures which could raise alarms during excessive seismic vibrations or during post-earthquake vibration-based damage detections.
One of the typical structures, built in the areas of strong seismicity to resist earthquakes are steel or reinforced concrete (/) moment resisting frames. Modern methods of seismic design of these structures take account of their ductile behavior during earthquakes. What is more they are designed in such a way that the energy released during damaging vibrations is concentrated in specially dedicated areas of these structures, in form of plastic hinges located usually at column/beam joints. Such the approach in structural design makes it possible to control (to some extent) the damaging vibrations and safely evacuate people even if the structure is partially damaged during the earthquake.
Among various sensors measuring mechanical vibrations recently emerged sensors measuring rotation rate (rotation velocity) [2], with applications in aeronautics, vehicle motion control, popular electronics (smartphones) or in seismic engineering and geophysics (e.g. Igel et al. 2012 [3]). In recent papers by Kokot and Zembaty [4], as well as Zembaty et al. [5, 6] the application of rotation rate sensors in SHM was verified by numerical simulations and in small laboratory scale. The purpose of this paper is to test yet one more area of their potential application, namely their ability to monitor plastic hinge formation (Fig. 1) during damaging vibrations of the structure. For this purpose, a numerical analysis of seismic, inelastic response of a moment resisting frame is carried out and presented in detail.
2. Plastic hinges
Plastic hinges form in bar structures during seismic vibrations based on the assumption that nonlinear behavior of the system carrying seismic loads is concentrated at the ends of the load-carrying elements - beams and columns. Properties of plastic hinges are important in determining modes of non-linear response of global structural response under seismic excitations [7].
As it was already indicated, concentrated plasticity is the most commonly used approach in modern seismic design. A properly developed, concentrated plastic hinge appears depending on various factors: mechanical properties of reinforcement and its details, reinforcement ratio, concrete compressive strength, cross-section shape and level of confinement [8].
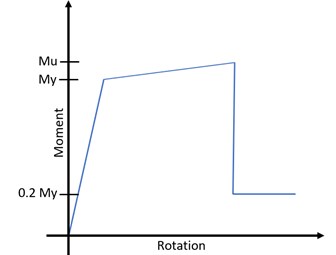
Many commercial software programs are available to perform nonlinear analyses using a concentrated plasticity approach. In SAP2000, the nonlinear behavior of structural elements can be modeled through automated-hinge or user-defined hinge models, which are commonly used during structural design process according to seismic design codes such as FEMA [9, 10]. A simplified nonlinear hinge behavior used in presented analysis is explained in Fig. 2, in which is yield moment, is ultimate moment capacity.
Fig. 2Adaptation of ideal moment-rotation curve in SAP2000
3. Example reinforced concrete frame
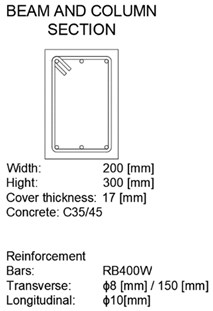
For this analysis, the simplest possible, / moment resisting frame subjected to horizontal seismic excitations was chosen (Fig. 3). The frame is made of concrete C35/40 and consists of a beam and two columns with the same cross-section (Fig. 3). It has traditional hinges in all its nodes apart from the node 3, where the respective plastic hinge is to develop. The reinforcement consists of 3 bars Ø10 mm (RB400W) in the upper and lower part of the cross-section. In addition, stirrups Ø8 mm placed in 150 mm distance are applied against shear forces.
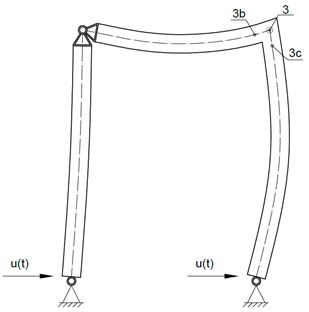
Fig. 3A reinforced concrete frame under seismic excitations ut with 2 rotational degrees of freedom (3b and 3c) to monitor plastic hinge development of node 3
a)
b)
4. Numerical analysis
The frame was modeled using Finite Element Method (FEM) program SAP2000. The FEM mesh is concentrated about the stiff joint ‘3’, making it possible to retrieve rotation coming from the plastic hinge development by observing rotation difference of points 3b and 3c and to obtain the rotation difference (Fig. 3):
where (Fig. 4) – rotation of point 3b, – rotation of point 3c.
Fig. 4Behaviour of column-beam connection during plastic deformation: a) „opening”, b) „closing”
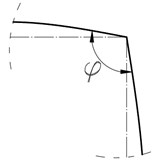
a) > 90°
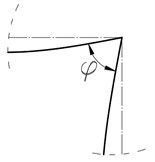
b) < 90°
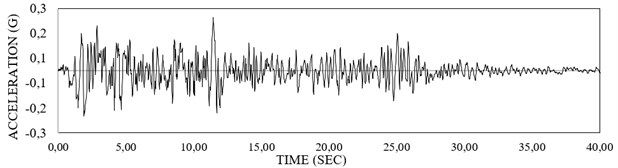
Fig. 5EL Centro earthquake acceleration record – May 18, 1940, East-West component
For intact structure at the rest, the column-beam angle stays equal to 90°. This angle is not kept during the vibrations and some residual rotation appear when a plastic hinge starts to develop.
The frame is excited by the familiar El Centro seismic record (Fig. 5) with a multiplier denoted as and changing from 0.1 to 2.5 so that various levels of seismic response is obtained: from linear to strongly inelastic.
During non-linear seismic vibrations (higher values of the multiplier ) the elements of the frame are damaged, and the response is reduced compare with the linear seismic response (low values of ).
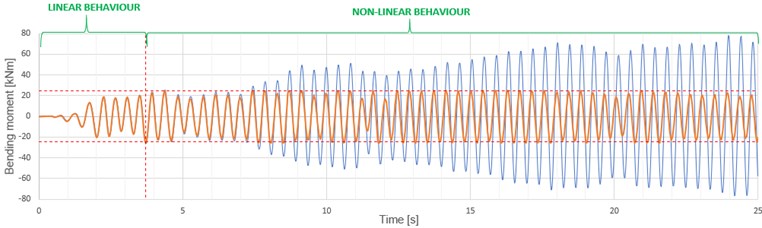
Fig. 6Comparison of linear and nonlinear frame behavior under seismic excitations: a) linear and nonlinear bending moment in node 3, b) rotation difference between auxiliary nodes ‘3b’ and ‘3c’, c) wavelet map of nonlinear bending moment response with parameter ‘a’ standing for scale of the wavelet, d) wavelet map of the rotation difference of node 3 shown in plot (b)
a)

b)

c)

d)
SAP2000 program by definition places plastic hinges in places of maximum bending moment concentrating energy release in these places. In Fig. 6(a) the bending moments in node ‘3’ of the frame are shown as function of time for linear response (linear structural properties turned ‘on’ in SAP code – blue plot) and inelastic response (non-linear response turned ‘on’ in SAP – red plot).
It is interesting to note how clearly the plastic hinge development is shown by observing rotation difference of points 3b and 3c (Fig. 6(b)) compare to observations of the time history of the bending moment (Fig. 6(a)). This makes the proposed method of monitoring inelastic seismic response by putting rotational sensors in appropriate nodes of the structure very effective. These differences of the seismic response are also clearly observed in respective wavelet maps of the bending moment response (Fig. 6(c)) and of the rotation difference response (Fig. 6(d)). The idea of using rotational sensors for this purpose makes it possible to declare ‘alarms’ when first plastic damages appear, or even to quantify these alarms with respect to the seriousness of the damages accumulated by using various parameters of the response, taken for example from respective wavelets. In Fig. 7 the inelastic rotation differences are shown for various values of the multiplier .
Fig. 7Rotation difference in node 3 of the frame from Fig. 3 for various seismic intensities (values of the K multiplier changing from 0.1 to 2.5)
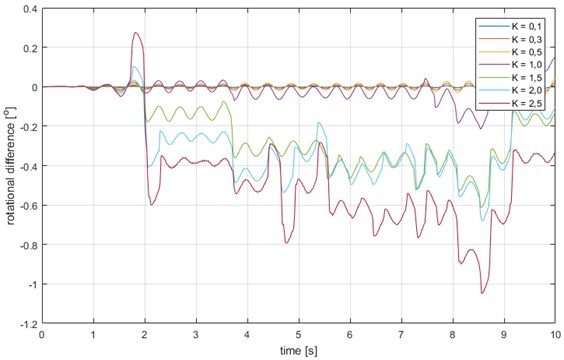
It can be seen that the higher are the levels of excitations, the higher is the rotational difference of points 3b and 3c, clearly reflecting structural damage accumulation.
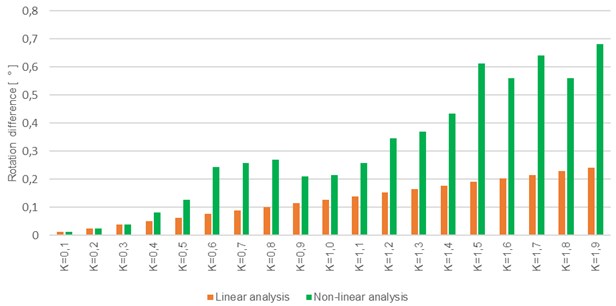
In Fig. 8 the peaks of rotational differences are shown (with increasing multiplier). The first damages start to appear at 0.4. It is interesting to note a nonuniform behavior of peak rotational difference with increasing intensity, yet the trend properly indicating the plastic response (green bars) can clearly be seen in comparison with peak linear response (red bars).
Fig. 8Plot of peak rotational response (rotational difference) as a function of seismic intensity (K multiplier)
5. Conclusions
Nonlinear time-history seismic response analysis of a simple moment resisting frame under seismic excitations with increasing intensity is presented with the aim at observing plastic hinge development in selected node of the structure. Taking into account rapid development of sensing techniques of mechanical vibrations of various structures, from airplanes to smartphones, a novel vibration measurement method using rotation rate sensors is tested to be applied in Structural Health Monitoring of building structures during damaging seismic vibrations. The purpose of the presented analysis was to numerically verify if measuring rotations of the plastic hinge node could be a good measure for SHM monitoring purposes.
It was demonstrated that observations of such the rotational response of a structural node could be a very good parameter of structural response for the purposes of SHM of the moment resisting frames. This way the developments of plastic hinges in moment resisting frames could easily be monitored as part of their design as potential ‘intelligent’ structures which can raze alarms during devastating earthquakes. For this purpose, one can develop an automatic software system remotely acquiring selected structural responses and taking advantage of various vibration parameters e.g. instantaneous spectral densities like wavelet maps which, in this analysis clearly indicated plastic hinge development based on the measured rotation difference at the plastic hinge.
References
-
Soon H., Farrar C. R., Hemez F. M., Shunk D. D., Stinemates D. W., Nadler B. R. A Review of Structural Health Monitoring Literature: 1996–2001. Los Alamos National Laboratory Report, LA-13976-MS, 2004.
-
Meydan T. Recent trends in linear and angular accelerometers. Sensors and Actuators A: Physical, Vol. 59, Issue 1, 1997, p. 43-50.
-
Igel H., Brokesova J., Evans J., Zembaty Z. Preface to the special issue on advances in rotational seismology: instrumentation, theory, observations and engineering. Journal of Seismology, Vol. 16, Issue 4, 2012, p. 571-572.
-
Kokot S., Zembaty Z. Vibration based stiffness reconstruction of beams and frames by observing their rotations under harmonic excitations – numerical analysis. Engineering Structures, Vol. 31, Issue 7, 2009, p. 1581-1588.
-
Zembaty Z., Bobra P., Bońkowski P. A., Kokot S., Kuś J. Strain sensing of beams in flexural vibrations using rotation rate sensors. Sensors and Actuators A: Physical, Vol. 269, 2018, p. 322-330.
-
Zembaty Z., Kokot S., Bobra P. Application of rotation rate sensors in an experiment of stiffness reconstruction. Smart Materials and Structures, Vol. 22, Issue 7, 2013, p. 077001.
-
Köroğlu M. A., Arslan M. H., Körez M. K. Use of regression analysis in determining the length of plastic hinge in reinforced concrete columns. System, Vol. 13, 2014, p. 4908.
-
Inel M., Ozmen H. B. Effects of plastic hinge properties in nonlinear analysis of reinforced concrete buildings. Engineering Structures, Vol. 28, Issue 11, 2006, p. 1494-1502.
-
Prestandard and Commentary for the Seismic Rehabilitation of Buildings. FEMA, Washington DC, USA, 2000.
-
Software Manual: SAP2000. Computers and Structures, Inc., Walnut Creek, California, USA, 2017.
