Abstract
The vibration dampers, shock absorbers, seismic isolation, bearing seals, compensation devices are widely applied in civil engineering, machine manufacturing and shipbuilding, aviation and aerospace engineering. For these details fabrication elastomeric materials are used. Rubber and rubber-like materials (elastomers) have the capability of absorbing input energy much better than other engineering materials. Elastomeric materials give many engineering advantages due to their high elasticity, good dynamic properties, low volume compressibility, a linear relationship between stress and strain at small and middle deformation, resistance to aggressive environmental factors. The disadvantage of elastomeric materials is ageing, i.e. changing their mechanical properties over time and lowering their operational capability. In given paper the influence of ageing of elastomeric materials on the damping properties of shock absorbers is considered based on the mechanical models of elastomers - Maxwell and Burgers modes.
1. Introduction
At present time, under conditions of intensification of manufacturing processes, increasing of the equipment capacity and high – speed vehicles creation, the questions of preventing the harmful effects of vibration and impacts on machines and construction elements require particular care. In most cases it is necessary to provide of shock and vibration protection devices at the design stage and these devices must retain their properties during the certain time [1-5].
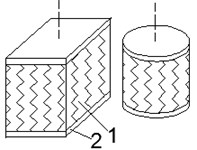
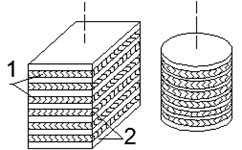
Elastomers, i.e. rubber and rubber-like materials, are most suitable material for shock absorbers and vibration isolators manufacturing due to their capability of absorbing input energy much better than engineering materials. These materials have unique properties: high elasticity, resistance to aggressive environmental factors, good dynamic properties, low volume compressibility, a linear relationship between stress and strain up to strain of 15-20 %. Elastomers are widely used in machine building, shipbuilding, civil engineering, aviation and aerospace as compensation devices, vibration dampers, shock absorbers [1-4]. Reinforced elastomers consist of alternating thin layers of elastomer and rigid reinforcing layers, connected by means of vulcanization or gluing. Packages of thin-layered rubber-metal elements (TRME) are used as bearing, compensating devices and may be successfully used as vibration absorbers for lateral vibration. Schemes of typical elastomeric shock absorbers are presented in Fig. 1.
The disadvantage of elastomeric materials is ageing, i.e. changing its properties with time even it does not operate under load. When considering aging, it is assumed that the parameters of corresponding model of elastomer slowly change their values with time. In this paper, it is proposed to account the aging of rubber by multiplying the constants of elastomeric material in Maxwell and Burgers models by special functions of time [6-8].
The aim of this work is to determine the dependence of damping properties of rubber vibration isolator on time for simplified model with one degree of freedom (ODF) system under action of harmonic excitation. The damping capacity are determined as the ratio of the amplitudes of the induced and forcing oscillations. For elastomeric impact absorber the changing of velocity restitution, displacement and impact force are also considered. Such approach allows to appoint the dimensions of ant vibration devices at design stage.
Fig. 1Schemes of typical elastomeric shock absorbers: a) solid, b) blocks of TRME; 1 – elastomer, 2 – rigid plate
a)
b)
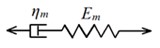
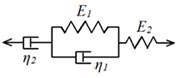
Fig. 2Mechanical models of viscoelastic media: a) Maxwel’s model, b) Burgers model
a)
b)
2. Mathematical model of ageing phenomena
Aging of the elastomeric materials is changing in time their mechanical properties under the influence of air or aggressive media. The duration of this process is large even in comparison with the relaxation time. Usually for clear presentation of elastic and dissipative processes in elastomers simple mechanical models are used; 4-elements Burgers model, including 2 modules of elasticity , , and 2 viscosity coefficients and , is considered the best (Fig. 2) [7, 8].
The relationship between stress and strain in time is described by the differential equation, which provide coincidence with the experiment. Therefore, the accounting of aging is usually performed by a multiplying of the material model constants on the empirically determined functions of time. For Burgers model the relationship between stress and strain is expressed by the equation:
where – normal stress, – relative deformation, – Young’s modulus, –viscosity factor.
In the particular case if Burgers model is transforming into Maxwell model, which quite well describes the creep before destruction:
When aging is taken into account in accordance with Eq. (1) or (2) it is assumed that the parameters , , , change their properties very slowly. To generalize the results, taking into account the temperature changing, the dependencies are given in the reduced time [7]:
The experiment confirms the possibility of taking an approximation:
For Maxwell model the relationships are:
The value of Burgers model constants , , , and corresponding them , , , are estimated and tabularized for some kinds of rubbers, as well as value , , , for Maxwell model. These constants, taken from [7], are presented below in Table 1 and 2.
To obtain creep under the condition const assuming Maxwell model of rubber, if the stress is applied at time , the strain at time is equal to:
3. Model of damping capacity and its changing in time for ODF vibroisolation system
In order to trace how the age of rubber effect on the service properties of elastomeric devices we consider the damping properties of rubber shock absorber, fatigue is not taken into account. Simplified one-degree-of-freedom (ODF) model of elastomeric vibroabsorber is best suited to estimation of damping capacity, it allows to obtain explicit analytical dependences for damping characteristics. Model presented in Fig. 3 with uniaxial compression – tension in -direction is considered below: elastomeric absorber in the form of rectangular prism or right circular cylinder is placed between protected object and vibrating base with kinematic excitation in accordance with time dependence of . The time dependence of the movement of the protected object is . Rubber element 1 is rigidly attached to plates 2.
Fig. 3a) Scheme of the vibroabsorber installation under vertical vibration and b) its design model; 1 – rubber element, 2 – undeformable plates; Δ – static deformation caused by Pz
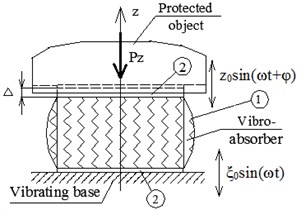
a)
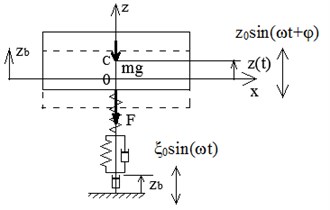
b)
In previous works of authors formulas for the damping capacity of vibroisolator under uniaxial harmonic excitation were derived for different models of elastomers [8, 9]. Damping capacity are expressed by the ratio of amplitude of the induced oscillation of object to the amplitude of the driving vibration of base . For Maxwell model of the elastomer we have [9]:
for the case of resonance, i.e. :
where – exciting frequency, – protected object natural frequency.
In case of ageing, taking into account Eq. (5) we have:
where – natutal frequency of protected object after rubber ageing.
For the case of resonance with ageing () it is obtained from Eq. (8):
For Burgers model of elastomer ratio received in [10] is equal:
For the case of resonance if from Eq. (10) it is received:
In order to take into account ageing it is necessary to substitute into the Eqs. (10) and (11) instead of constants , , , expressions , , , in accordance with Eq. (3) and (4) and instead of . Since is considered as initial modulus in Burgers model natural frequencies are assumed: .
For numerical examples the available data of rubbers were taken from [7]. The constants and the aging coefficients of Maxwell model are presented in Table 1, of four-elements Burgers model – in Table 2. The numbers in column 7 in Table 1 show the tangent of the inclination angle of the resonance curve to the axis without ageing, in column 8 – taking into account 3-years aging in accordans with Eq. (9). The numbers in column 8 in Table 1 and in column 11 in Table 2 show the factor of changing of natural frequency in 3 years ageing with accordance to Eqs. (8) and (12).
Table 1Maxwell models’ parameters
Rubber grade | MPa | MPa·s | ·104 1/day | ·104 1/day | s | s | ||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
1 | 8157 | 2.55 | 1.04 | 0.220 | –1.539 | 0.408 | 0.331 | 1.012 |
2 | 8164 | 1.91 | 1.17 | –0.087 | –0.241 | 0.613 | 0.582 | 0.996 |
3 | 8470 | 3.55 | 8.92 | 1.630 | –0.737 | 2.513 | 1.960 | 1.086 |
4 | 8508 | 2.44 | 5.60 | 1.500 | 7.280 | 2.295 | 3.542 | 1.079 |
5 | 8871 | 1.23 | 1.16 | 0.650 | 3.160 | 0.943 | 1.185 | 1.035 |
6 | 10429 | 3.38 | 3.60 | 0.085 | 0.466 | 1.065 | 1.109 | 1.005 |
7 | 1008 | 0.87 | 5.10 | –0.029 | 0.299 | 5.862 | 6.073 | 0.998 |
Table 2Burgers models’ parameters
Rubber grade | MPa | MPa | MPa·s | MPa·s | ·104 1/day | ·104 1/day | ·104 1/day | ·104 1/day | ||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1 | 8157 | 3.58 | 8.93 | 0.057 | 1.04 | 0.54 | –0.370 | 1.650 | –1.539 | 1.029 |
2 | 8164 | 2.43 | 8.85 | 0.588 | 1.17 | –0.091 | –0.140 | –0.067 | –0.241 | 0.995 |
4 | 8508 | 3.30 | 9.31 | 0.724 | 5.60 | 1.23 | 1.170 | –0.065 | 7.280 | 1.065 |
5 | 8871 | 1.63 | 5.09 | 0.363 | 1.16 | 0.81 | 0.330 | –0.240 | 3.160 | 1.043 |
6 | 10429 | 4.28 | 16.5 | 0.442 | 3.60 | 0.05 | 0.057 | 0.009 | 0.466 | 1.003 |
7 | 1008 | 1.62 | 1.88 | 0.091 | 5.10 | 0.15 | –0.080 | –0.110 | 0.299 | 1.008 |
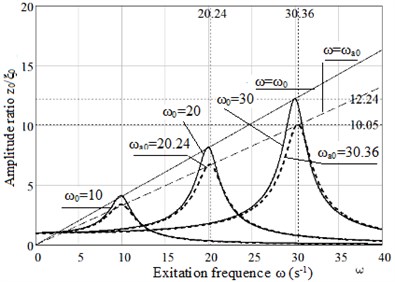
The results of investigation of aging influence on damping properties of vibroisolator are presented below. The dependence of amplitude ratio on excitation frequency is given in accordance with Maxwell model in Fig. 4, in Fig. 5 – in accordance with Burgers model. Time of aging is assumed three years. For both models three natural frequencies is examined: 10, 20, 30 s-1 without aging, natural frequency increases with ageing.
Burgers model shows better damping properties in comparison with Maxwell model; the difference appears near resonance zone, in post-resonance zone (here 40 s-1) the results of both model are coincided. The obtained results correspond to the well-known fact of the theory of vibration: if natural vibration frequency of object is three times smaller than the frequency of the driving oscillations, then the amplitude of object oscillations is attenuated by about 10 times.
Fig. 4Plots of dependence amplitude ratio x0/ξ0 on excitation frequency ω for Maxwell model: for natural frequency of protected object ω0= 20 s-1 and different types of rubbers
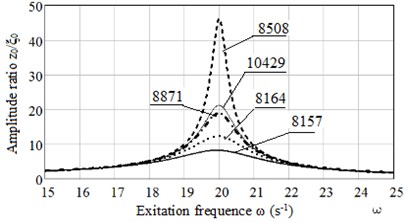
a) Without ageing
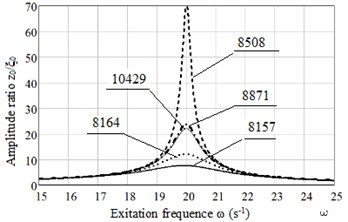
b) Accounting 3 years aging
Fig. 5Plots of dependence the amplitude ratio x0/ξ0 on excitation frequency ω for rubber 8157: without ageing, taking into account ageing 3 years
a) Maxwell model
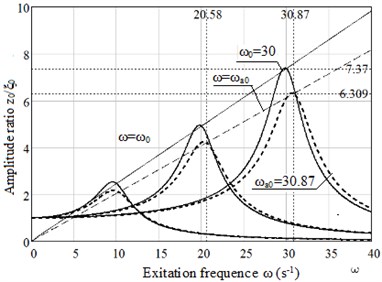
b) Burgers model
4. Changing the characteristics of impact absorber as the result of elastomers ageing
In this part the influence of aging on the restitution coefficient of rubber shock absorber is studied in case of direct central impact (Fig. 6). After collision of rigid body and rubber shock absorber they move together (absorber is deformed) in -direction till the velocity reaches zero value and then move in opposite direction till body and absorber disconnection. Mass and deformation of reinforcing plate 3 are not taken into account. The equation of body motion during impact:
where – impact force, – cross-section area of absorber, – initial height of absorber. Impact force is taken in accordans with Burgers model of elastomer. Substituting Eq. (12) and corresponding derivatives from Eq. (12) into Eq. (1), it is obtained:
The deformation of impact body and reinforcing plate is not taken into account. Eq. (13) is solved numerically under initial conditions: 0, 0, 1 m/s, 0; mass of body 20 kg, elastomeric cylinder dimensions 0.10 m and 0.08 m, rubber grade 8157. Plots of impact velocity is shown in Fig. 7: 0.934 m/s without ageing and 0.920 m/s after 3 years ageing. The displacement during impact 9.05 mm without ageing and 9.01 mm after 3 years ageing, impact force 2.68 kN and 2.66 kN accordingly.
Fig. 6Scheme of the impact of rigid body on shock absorber: 1 – impact body, 2 – rubber cylinder, 3 – reinforcing plates
Fig. 7Plots of dependence the impact velocity on time for rubber 8157
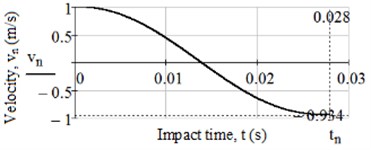
a) Without aging
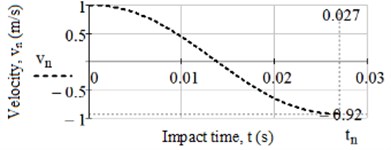
b) Taking into account aging 3 years
5. Conclusions
In this paper the influence of aging on the working properties of rubber shock absorbers is discussed. The changing of damping properties depending on aging for two mechanical models of elastomeric material – Maxwell and Burgers – are studied. Damping property is defined as ratio of amplitudes of forced vibration of protected body and forcing oscillation of base under harmonic excitation. For both models three natural frequencies is examined: 10, 20, 30 s-1 without aging and with 3 years of aging. Ageing of rubber increases natural frequency and decreases damping capacity. Burgers model shows better damping properties in comparison with Maxwell model; the difference appears near resonance zone, in post-resonance zone the results of both models are coincided.
The aging influence on restitution coefficient during impact was defined using Burgers model of elastomer. Ageing decrease restitution coefficient of absorber, deformation and impact force.
All numerical calculations were fulfilled using Mathcad-15.0 program.
This approach to estimation the damping capacity of vibration isolator and its decrease associated with the ageing of elastomers is first applied in engineering practice and requires experimental confirmation. An express method for determining the constants of 4-elements rheological model was developed by authors earlier [10]. The next step of our work is to determine the dependence of the variation of these parameters on time using accelerated ageing.
References
-
Gent A. N. Engineering with Rubber: How to Design Rubber Components. Carl Hanser Verlag, Munich, 2011.
-
Bauman J. T. Fatigue, Stress and Strain of Rubber Components: Guide for Design Engineer. Carl Hanser Verlag, Munich, 2008.
-
Kelly J. M., Konstantinidis D. A. Mechanics of Rubber Bearings for Seismic and Vibration Isolation. John Wiley and Sons, UK, 2011.
-
Konstantinidis D. A., Kelly J. M. Advances in low-cost seismic isolation with rubber. Proceedings of the 10th U.S. National Conference in Earthquake Engineering, 2014.
-
Iljushin A. A., Pobedrja B. E. Fundamentals of Mathematical Theory Thermo-Viscoelasticity. Nauka, Moscow, 1970, (in Russian).
-
Brown R. P., Bulter T., Hawely S. W. Ageeing of Rubber: Acceleration Heat Ageing Test Results. Smither Rapra Publishing, 2001.
-
Lyapunov V. T., Lavendel E. E., Shlyapochnikov S. A. Rubber Vibration Isolators: Habdbook, Sudostrojenie, Leningrad, 1988, (in Russian).
-
Polukoshko S., Martinovs A., Sokolova S. Aging, fatigue and durability of rubber vibration isolation elements. Proceeding of the 11th International Scientific and Practical Conference: Environment, Technology, Resources, Vol. 3, 2017, p. 269-275.
-
Polukoshko S. Estimation of damping capacity of rubber vibration izolators under harmonic exitation. Vibroengineering Procedia, Vol. 8, 2016, p. 50-56.
-
Martinovs A., Polukoshko S., Apeinans E., Zaicevs E. Determination constants of 4-element rheological model with rebound resilience method. Proceedings of the 16th International Scientific Conference Engineering for Rural Development, Vol. 16, 2017, p. 924-931.
