Abstract
The vibration-isolating rate of vibration isolating slot under buried pipe subjected to blasting seismic waves can been investigated by using the numerical method. For achieving a good vibration isolating effect, the depth of the vibration-isolating slot needs to be larger with the increase of the depth of the pore. The difference of the super-depth h leads to the difference in the trend of vibration isolating. The depth of the vibration-isolating slot is larger than the depth of the hole, which can improve the vibration-isolating rate. The different type of rock and soil medium is a significant effect on the vibration-isolating rate. To obtain ideal vibration-isolating effect, vibration-isolating slot depth compared with pipeline buried depth is greater than a certain value.
Highlights
- The vibration-isolating rate of vibration isolating slot under buried pipe subjected to blasting seismic waves can been investigated by using the numerical method.
- For achieving a good vibration isolating effect, the depth of the vibration-isolating slot need to be larger with the increase of the depth of the pore.
- The difference of the super-depth h leads to the difference in the trend of vibration isolating.
- The depth of the vibration-isolating slot is larger than the depth of the hole, which can improve the vibration-isolating rate.
- To obtain ideal vibration-isolating effect, vibration-isolating slot depth compared with pipeline buried depth is greater than a certain value.
1. Introduction
When an explosive explodes in the rock mass, it will release a huge amount of energy. Apart from the breaking of the rock, some of the energy propagated outward in the form of waves to form seismic waves. Although the energy of the seismic wave is only a small part of the explosive energy, it will cause some harm to the oil and gas pipeline, if it is not controlled or controlled properly. Therefore, it is necessary to take effective measures to control the blasting vibration in the safety range. In view of the causes and propagation characteristics of blasting vibration, many effective measures have adopted to control the vibration caused by explosion. The vibration-isolating slot is widely used in explosion engineering because of its good vibration-isolating effect and barrier function. The vibration-isolating slot can obstruct the propagation of the blasting seismic wave to the oil and gas pipeline, which reduce the blasting vibration and the damage to the oil and gas pipelines.
Lou Jian-wu et al. [1] studied the propagation law of deep-hole blasting seismic wave in a depth 8 m, length 38 m, width l0 m vibration-isolating slot. With the analysis of the measured data, the proportion of distance is 0.018-0.038 (kg1/3·m-1), vibration-isolating effect of vibration-isolating slot to blasting seismic waves is best, vibration-isolating rate can reach 50-70 %. Prakash et al. [2] conducted experiments on the impact of slot depth on the vibration-isolating rate. The ratio of slot depth and pore depth was 0.3, 1.0 and 1.125, and the vibration-isolating rate was 16.6-55 %. Venkatesh [3] studied the peak vibration velocity of the particles on both sides of the slot when the depth of the vibration-isolating slot was more than the hole depth, and obtained the vibration-isolating rate between 11-18.5 %. Meng Hai-li et al. [4] simulated the propagation process of stress wave using ANSYS/Ls-dyna software, analyzed the attenuation rule of the stress wave near the pre-crack and obtained the pre-fracture of no material, and the vibration-isolating rate was over 90 %. The pre-fracture vibration-isolating rate of the filling cuttings was 61.37 %. Anony [5] according to the dynamic’s theory, used the finite element program, analyzed damage model of modified fragmentation effect on surrounding rock under different ways of initiation.
In addition to the structural parameters of the vibration-isolating slot, the vibration-isolating rate of the vibration-isolating slot influenced by various factors such as blasting geology (site media), blasting parameters, depth of pipe, and the distance of the pipe to the detonation zone. This paper investigated the vibration-isolating rate of vibration-isolating slot subjected to blasting seismic waves. The results obtained from the present study can used for improvement in protective design of steel pipelines.
2. Calculation model
According to the characteristics of the problem studied, the coupling algorithm of multi material Euler and Lagrange structure applied to calculate the interaction between explosives, air and other solid structures. In the actual modeling process, it defines explosives and air as Euler grids, and ensures the common nodes between them. It defines the site medium, the fine sand in the pipe trench, the backfill soil medium and the steel pipe as the Lagrange mesh. The interaction between the fine sand in the trench and the steel pipe adopts the surface-surface contact analysis, on contact surface in fine sand and steel pipe, steel pipe will take the master contact surface (Master Surface, for larger stiffness), soil for the slave contact surface (Slave Surface, relatively soft). Because the middle hole is located on the center line of the step width, in order to improve the mesh accuracy and save computing resources, we only need to establish the 1/2 model relative to the hole axis and adopt the g-cm-s system. In order to simulate accurately the detonation of explosives and their impact on surrounding rocks, the meshes of explosives and surrounding rock are dense when dividing the grid. Because the rock affected by blasting seismic waves, which is in the range of elastic deformation, so the mesh is sparse. The SOLID164 element used to mesh the three-dimensional model of the above numerical calculation.
3. Results and analysis
3.1. Super-depth
The important blasting parameters of the open pit step blasting are the pore diameter, pore depth, super-depth (or super-drill), block length and so on. The source of the blasting seismic wave is the charge in the gun hole. With the increase of the pore depth, the depth of the wave source is larger. In order to achieve good effect of vibration isolating, the larger the vibration-isolating slot depth is needed. In fact, for the same blasting engineering area, different blasting engineering parameter designers have their own design ideas and understanding, so it is possible to take different super-depth within a reasonable range. Therefore, the key blasting parameters of the open deep-hole step blasting are worthy of our special attention.
Keep bench height, pore diameter, pore spacing and row spacing, depth of the filling, charging length is unchanged, and deep respectively 1.5 m, 2.0 m, 2.5 m, 3.0 m (reference existing domestic mine blasting parameters of super-depth range). Finite element numerical calculation of the mathematical model is set up according to the above parameters, the numerical calculation model under various working conditions will submit Ls-dyna program to calculate file. The location the maximal vertical vibration extracted, through the post-processing software data. Fig. 1 shows the relationship between the vibration-isolating rate and the deep of the vibration isolating under four super-depth conditions.
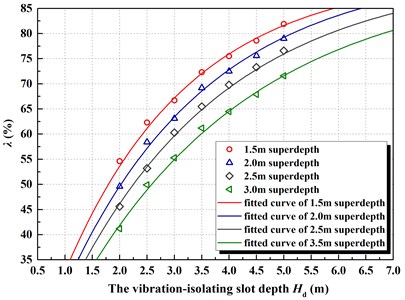
According to numerical calculation results, the data is fitted with the super-depth = 1.5 m, 2.0 m, 2.5 m and 3.0 m respectively, and it can express by following equation:
In the formula, is vibration-isolating rate (%); is the depth of the vibration-isolating slot (m); is the natural constant, and the value is 2.718. The distribution of the four fitting formulas and their data points in Eq. (1) shown in Fig. 2. It can be seen that the fitting effect of the expression type of this function is relatively good correlation.
The results show that for achieving a good vibration isolating effect, the depth of the vibration-isolating slot need to be larger with the increase of the pore depth. In addition, it can be shown from Eq. (1) that the maximum difference of each fitting formula is the power index value, which should lead to the difference in the trend of vibration isolating, due to the difference of the super-depth . As a result, the fitting formula reflects the important message, namely for the same open blasting region, blasting in many different ways of design parameters summed up, the super depth (charge depth) is a critical parameter, and it can reflect the power index values in fitting formula, the smaller the charge is, the larger the power exponent is. This conclusion for actual engineering design has very important reference value, namely, to obtain ideal vibration-isolating effect, the depth of the vibration-isolating slot is larger than that of the pore depth.
Fig. 1The vibration-isolating rate λ of the different super-depth
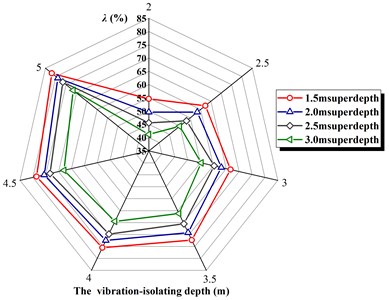
Fig. 2The relationship curve between vibration-isolating rate λ and depth Hd with the different super-depth h
3.2. Propagating medium
The blasting seismic wave propagated in rock and soil medium, which has the characteristics of medium structure and physical and mechanical properties. When blasting seismic waves pass the rock and soil medium, physical and mechanical properties and the original structure properties are different, which lead to a certain difference of the dynamic response in the propagation and attenuation characteristics. The use of the M.·A.·Sadov empirical formula can predict the intensity of blasting seismic waves, which also takes into account the impact of blasting seismic wave propagation media. In the process of actual engineering construction, the oil and gas pipeline laid in the rock and soil medium with different characteristics. Therefore, it is necessary to consider the medium factors of surrounding rock and soil in the explosion zone during the study. For this purpose, three representative geotechnical media selected for calculation, namely, medium granites (hard rock), hard limestone (medium hard rock) and medium solid marl (soft rock). The related physical and mechanical properties parameters of the three types of rock and soil shown in Table 1.
In order to study vibration-isolating effect of the propagating medium on blasting seismic wave, the research based on the blasting pore network parameters. It is to maintain the height of the steps, pore diameter, pore spacing, row spacing, filling depth, depth, and length of charge, while the explosive zone medium is different. The finite element numerical calculation model is set up according to the above principles, it will submit Ls-dyna program to calculate file under various working conditions and extract the maximal vertical vibration through the post-processing software data. Fig. 3 shows the relationship between the vibration-isolating rate and the deep of the vibration-isolating in three kinds of rock and soil.
Table 1The physical and mechanical properties parameters of the three types of rock and soil
Type | Density (kg/m3) | Modulus of elasticity (GPa) | The bulk modulus (GPa) | Shear modulus (GPa) | Poisson’s ratio | The compressive strength (MPa) |
Medium granites | 2680 | 62.80 | 40.92 | 28.42 | 0.26 | 160 |
Limestone | 2490 | 48.67 | 25.95 | 20.58 | 0.29 | 116 |
Marl | 2370 | 33.40 | 20.72 | 16.46 | 0.31 | 55 |
According to the above numerical calculation results, the calculation data of rock and soil media in the three detonation zones fitted, which expressed by Eq. (2):
In the formula, is vibration-isolating rate (%); is the depth of the vibration-isolating slot (m); is the natural constant, and the value is 2.718. The distribution of the three fitting formulas and their data points in Eq. (2) shown in Fig. 4. The fitting effect of the expression type based on this function still presents a relatively good correlation.
Fig. 3The vibration-isolating rate λ in three kinds of rock and soil
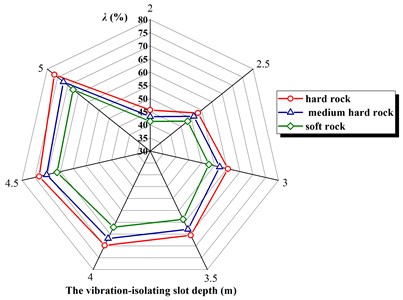
Fig. 4The relationship curve between vibration-isolating rate λ and depth Hd with the different rock and soil
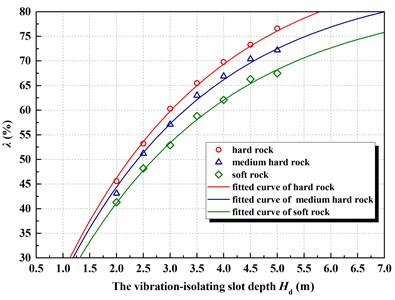
The results show that there is a significant effect on the vibration-isolating rate of rock and soil. It shown from the calculation results that with the increase of the depth of the vibration-isolating slot, the difference is slightly increased. In addition, it can be seen from Eq. (2) that there is a slight difference in the power index value of each fitting formula, and its biggest difference lies in the coefficient outside the formula parenthesis (referred to the influence coefficient of blasting dielectric). As a result, the fitting formula reflects the important message is that the explosive medium influence coefficient is a key parameter, for different blasting open regional site media and similar blasting parameters. This conclusion is of great reference value for the design of vibration-isolating engineering.
3.3. Buried depth
Specified in the specifications for engineering design of transmission gas pipeline: “laying pipeline should be buried way, the layer soil thickness of buried pipeline should comply with the provisions of the Table 2. When It can’t meet the requirements of layer soil thickness, external load is larger, external operations may endanger pipeline, protection measures should be taken”.
Table 2Minimum layer thickness (m)
Regional level | Soil type | Rock | |
Dry land | Paddy field | ||
Level 1 | 0.6 | 0.8 | 0.5 |
Level 2 | 0.6 | 0.8 | 0.5 |
Level 3 | 0.8 | 0.8 | 0.5 |
Level 4 | 0.8 | 0.8 | 0.5 |
The above specification only specifies that the minimum layer soil thickness is the depth of the pipe (from the top of the pipe). In actual engineering, burial depth is actually a certain range. We need to study the influence rule of deep on the vibration-isolating rate of different pipelines, under certain blasting parameters and vibration-isolating slot.
In order to study the effect of buried depth on vibration isolating, the parameters of blasting holes are set up. Particular way is to keep bench height, pore diameter, pore spacing and row spacing, depth of the filling, charging length is unchanged, and the pipeline buried depth were taken according to actual condition of 0.5 m, 1.2 m, 2.0 m, 2.5 m (reference existing domestic mine blasting parameters of super-depth range). The finite element numerical calculation model is set up according to the above principles, a numerical calculation model under various working conditions will submit Ls-dyna program to calculate file and extract the maximal vertical vibration through the post-processing software data. Fig. 3 shows the relationship between the vibration-isolating rate and the deep of the vibration-isolating under different buried depth conditions.
Fig. 5The vibration-isolating rate λ under different buried depth
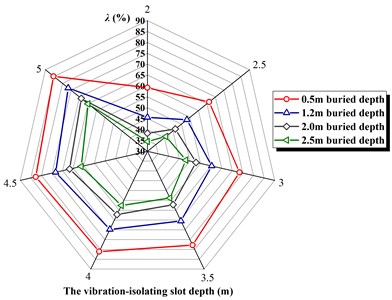
Fig. 6The relationship curve between vibration-isolating rate λ and depth Hd under different pipe buried depth
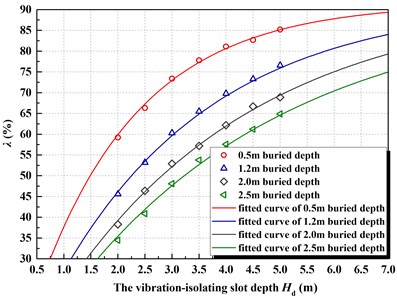
According to the above numerical calculation results, the calculation data of buried deep in different pipelines fitted, which expressed by Eq. (3):
In the formula, is vibration-isolating rate (%); is the depth of the vibration-isolating slot (m); is the natural constant, and the value is 2.718. The distribution of the fitting formula and its data points in Eq. (3) shown in Fig. 6. The fitting effect of the expression type of this function still shows a good correlation.
The calculation results show that the depth has a significant effect on the vibration-isolating ratio. Under the condition of certain super-depth pore, the larger the pipe depth is, the lower the vibration-isolating rate is. In the case of large pipe buried depth, if the intensity peak of blasting seismic wave exceeds the allowable threshold value of the pipeline vibration, it needs a large depth of vibration-isolating slot to achieve a good vibration-isolating effect. This gives us some enlightenment that the depth of the vibration-isolating slot in the actual project should be at least greater than the depth of the pipe. In addition, it shown from Eq. (3) that the maximum difference of each fitting formula is the power index value, which should be the difference in the vibration-isolating trend, due to the difference of the buried depth of the pipe. Therefore, the important information reflected in the fitting formula is the influence of the buried depth , which reflected as the power exponent value in the fitting formula. That is, the lower the depth is, the greater the power exponent value is. This conclusion for actual engineering design of vibration-isolating slot has very important reference value. To obtain ideal vibration-isolating effect, vibration-isolating slot depth compared with pipeline buried depth is greater than a certain value.
4. Conclusions
1) For achieving a good vibration isolating effect, the depth of the vibration-isolating slot needs to be larger with the increase of the depth of the hole. The difference of the super-depth leads to the difference in the trend of vibration isolating. The depth of the vibration-isolating slot is larger than the depth of the hole, which can improve the vibration-isolating rate.
2) The different type of rock and soil medium is a significant effect on the vibration-isolating rate. There is explosive engineering with different blasting media and similar blasting parameters. The medium influence coefficient of explosive region is a key parameter, which is of great reference for the design of vibration-isolating engineering.
3) The depth has a significant effect on the vibration-isolating ratio. The depth of the vibration-isolating slot in the actual project should be at least greater than the depth of the pipe. To obtain ideal vibration-isolating effect, vibration-isolating slot depth compared with pipeline buried depth is greater than a certain value.
References
-
Lou Jian Wu, Long Yuan, Zhou Xiang Damping ditch effect in propagation of blasting seismic wave and its analysis. Mining and Metallurgical Engineering, Vol. 24, Issue 1, 2004, p. 11-15.
-
Prakash A. J., Palroy P., Misra D. D. Analysis of blast vibration characteristics across a trench and a pre-split plane. Fragblast, Vol. 8, Issue 1, 2004, p. 51-60.
-
Venkatesh H. S. Influence of Explosive Charge on Blast Vibrations in Surface Mines. NITK, Mangalore University, 2002.
-
Meng Hai-Li, Deng Zhi-Chao Numerical simulation study on the law of presplitting blasting vibration. Railway Engineering, Vol. 1, 2008, p. 74-78.
-
Ls-dyna Vibration of use manual (Version 971/Release 4). Anony, Livermore Soft Ware Technology Corporation, Vol. 37, Issue 10, 2013, p. 475-482.
-
Chen Jian-Ping, Gao Wen-Xue Geology of Blasting Engineering. Science Press, Beijing, 2005.
About this article
This research was financially supported by the National Nature Science Foundation of China, Nos. 51678567, 11102233 and 51608530.
