Abstract
A bispectral locally-preserving projection fault identification method is proposed. Fault pattern recognition is performed using a support vector machine (SVM). The experimental results show that the method can effectively identify the current damage of the bearing shaft, and the classification accuracy of the bearing fault containing the shaft current damage can reach more than 96.25 %.
1. Introduction
At present, the research on the shaft current is based on actual production, and summarizes the causes, hazards, and suppression measures of the shaft current [1-8]. Bispectral analysis can deal with non-stationary and non-Gaussian random series, and can theoretically completely suppress Gaussian noise. It has been widely used in the fault diagnosis of rotating machinery.
The manifold learning algorithm reveals the unique manifold structure of high-dimensional nonlinear data sets. [9-11]. Based on the above, this study uses bispectral local-preserving projection method to identify bearing shaft currents, performs envelope demodulation and bispectrum calculation of bearing vibration signals through Hilbert transform, and obtains bispectral amplitude eigenvector matrices. LPP reduces the dimensionality of the feature vector matrix to obtain low-dimensional fault features; finally, it uses support vector machines (SVM) to identify fault patterns. The experimental results show that this method can effectively identify bearing shaft current damage failure.
2. Rolling bearing vibration signal analysis
2.1. Bispectral definition and estimation
The random sequence, whose bispectrum is defined as a three-dimensional cumulant two-dimensional Fourier transform, is as follows:
In the formula, is Third-order cumulants. The actual calculation uses a finite-length observation sequence and the bispectrum is estimated using direct or indirect methods.
2.2. Locally held projection
The main idea of the LPP algorithm is to maintain closeness in the low-dimensional space after dimension reduction by making the points in the original space close to each other. it can effectively solve the problem of feature extraction of new samples.
3. Bispectral local preserving projection algorithm
(1) Original vibration signal , .
(2) The Hilbert transform is used to perform envelope demodulation on the vibration signals of different fault conditions.
Suppose signal among them is Carrier frequency, is the envelope of , is the phase modulation signal of. , is the frequency component of the modulation signal , is the initial phase angle of . Analyze signal .
(3) Bispectral estimation of demodulated signals. Fourier transform based on the vibration signal . Modulated signal bispectrum:
where is the conjugated number of , indicates mathematical expectation, is the carrier frequency, is the modulation frequency.
(4) Using LPP to reduce dimension of amplitude eigenvector matrix to obtain low-dimensional fault features.
Assume -dimensional high dimensional matrix samples , a set of vector matrix is obtained by projection through a -dimensional matrix , among them , .
The transformation matrix can be obtained by minimizing the following objective function:
where is the weight matrix, it can be defined with nearest neighbors:
where is the nearest neighbor of .
After the dimensionality reduction, the feature space can maintain the local structure of the original high-dimensional space:
Mapping function .
(5) Input the corresponding low-dimensional fault features of the test sample into the trained classifier SVM to identify the test sample fault status.
4. Wind turbine bearing shaft current damage identification
4.1. Experimental data
The simulation test bench for bearing axis current damage is shown in Fig. 2(a). The test bearing used in this experiment is a detachable deep groove ball bearing. The test stand includes 1 motor; 2 insulating joints; 3 main shafts; 4 support bearing seats; 5 carbon brushes; 6 test bearing housings; 7 vibration acceleration sensor; 8 insulated bearings; 9 base; 10 adjustable DC switching power supply.
Fig. 1Bearing shaft current damage test bench

Through the experiment, the outer ring fault bearing with axial current damage is obtained. Then, the outer ring pitting failure and inner ring pitting failure of the bearing are obtained by electric spark. The acquisition system of this experiment is a B&K acquisition system. The bearing model is 6205EKA. Its bearing parameters and characteristic frequency under the corresponding rotating speed are shown in Table 1. Bearings in different states are shown in Fig. 2.
Table 16205EKA deep groove ball bearing related parameters
Name | Numerical value |
Bearing outer diameter / mm | 52 |
Bearing inner diameter / mm | 25 |
Bearing width / mm | 15 |
Rolling body diameter / mm | 7.925 |
Bearing pitch diameter / mm | 39 |
Number of rolling bodies | 9 |
Contact angle | 0 |
Outer ring fault characteristic frequency / Hz | 71.7 |
Inner ring fault characteristic frequency / Hz | 108.3 |
Fig. 2Bearings in different states

a) Normal status

b) Axis current outer ring failure

c) Pitting outer ring failure

d) Pitting inner ring failure
4.2. Fault feature extraction
The function parameters of this experiment were set as follows: transform length, window function selection, number of estimated samples, percentage of overlap. The bispectrum of different bearing states are shown in Fig. 3, respectively.
It can be seen from Fig. 3 that the characteristic frequency of the bearing fault under different conditions, but it is difficult to distinguish the axial current outer ring fault and the pitting outer ring fault from the figure. However, after the bispectral estimation, the amplitude eigenvectors of different fault states are obtained and the fault feature extraction is preliminarily completed. The fault feature extraction and recognition effect of LPP algorithm fault feature extraction and bispectral local-preserving projection method is shown in Fig. 4.
It can be seen from Fig. 4 that the LPP method has a good ability to aggregate faults. The bispectral locally-preserving projection method can well identify bearing faults.
Fig. 3Bispectrum of different bearing states
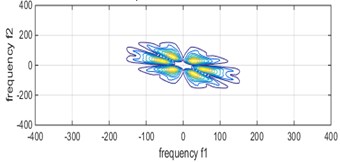
a) Normal status
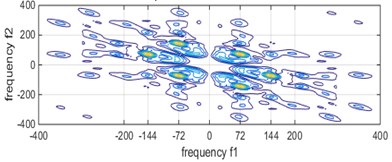
b) Axis current outer ring failure
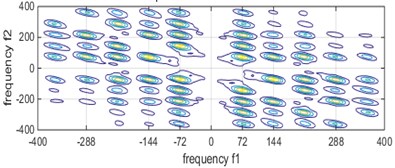
c) Pitting outer ring failure
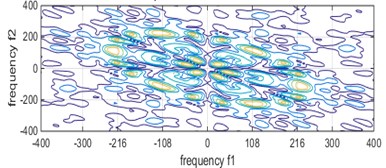
d) Pitting inner ring failure
Fig. 4Fault feature extraction and recognition effect of LPP algorithm and bispectral local-preserving projection
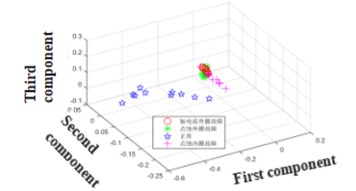
a) LPP
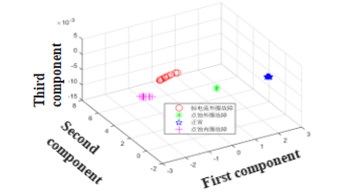
b) Bispectral localized projection
4.3. Support vector machine fault recognition effect
In order to quantify the classification effect, the fault feature obtained by the bispectral local hold projection method is identified by using the classifier LIBSVM developed by Dr. Lin Zhiren of Taiwan University. The fault state recognition effect of the SVM is shown in Table 2.
Table 2Support vector machine recognition effect
Name | Training samples | Training label | Test sample | Recognition rate |
Outer ring current damage fault | 20 | a | 20 | 95 % |
Outer ring pitting failure | 20 | b | 20 | 95 % |
Normal status | 20 | c | 20 | 100 % |
Inner ring pitting failure | 20 | d | 0 | 95 % |
Total recognition rate | 96.25 % |
The overall classification recognition rate has reached 96.25 %. This achievement has reached the requirements of the fault diagnosis system. The fault of the bearing shaft current damage is also well recognized.
5. Conclusions
Aiming at the problem that the fault bearing vibration signal of bearing shaft current in wind turbine is complex and it is difficult to extract effective fault features, a fault identification method based on bispectral locality-preserving projection is proposed. In this method, the bispectrum can effectively represent the running state information of the rolling bearing and has obvious differences in different fault types. The vibration signal of the bearing is envelope-spectrum-demodulated and bispectrum-estimated to obtain the amplitude eigenvector matrix. Due to the large dimension of the bispectral amplitude eigenvector matrix, the bispectral amplitude eigenvector matrix is reduced by the locality-preserving projection algorithm. The bispectrum is projected to the eigendimensional space under the condition that the bispectral local structure is invariable, and the low dimensional fault features of the bearing are obtained. The low dimensional feature vector is input into the SVM classifier to identify and judge the bearing fault. The experimental results show that the proposed method can effectively identify bearing shaft current damage faults, and the classification accuracy of bearing faults containing shaft current damage can reach 96.25 %.
References
-
Chen Guo Qiang, Chen Guo Zhong, XuMing Wind turbine generator shaft voltage and shaft current on the bearing and preventive measures. Shenhua Technology, Vol. 12, Issue 5, 2014, p. 60-62.
-
Xiong Li Jian Wind Power New Technology and Power Generation Engineering Design, Operation, Maintenance and Standard Specification Practical Handbook. China Science and Technology Press, Beijing, 2005.
-
Zheng Hai Bo Wind turbine vibration monitoring case analysis. Wind Energy, Vol. 7, 2014, p. 88-92.
-
Muetze A. Bearing Currents in Inverter-Fed AC-Motors. Techische Universitaet Darmstadt, Germany, 2004.
-
Don Macdonald, Will Gray PWM drive related bearing failures. IEEE Industry Application Magazine, Vol. 5, Issue 4, 1999, p. 41-47.
-
Prudhom Aurelien, Daviu Jose Antonino, et al. Time-frequency vibration analysis for the detection of motor damages caused by bearing currents. Mechanical Systems and Signal Processing, Vol. 84, 2017, p. 747-762.
-
Hua Cheng Gang, Zhang Ben Lian Analysis of shaft current of motors prevention of shaft current of gearboxes. Metallurgical Power, Vol. 2, 2014, p. 7-10.
-
Wang Guangbin, Du Moujun, Huang Liangpei, Li Long Prediction of bearing damage in wind turbines based on the quadratic root mean square of sub-band manifold. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2017, https://doi.org/10.1177/0954406217735553.
-
Zhang Shao Hui, Li Wei Hua Locality preserving projections based on feature space denoising and its application in bearing fault classification. Journal of Mechanical Engineering, Vol. 50, Issue 3, 2014, p. 92-99.
-
Deng Shi Jie, Tang Li Wei, Zhang Xiao Tao Gear fault diagnosis based on an adaptive neighborhood incremental PCA-LPP manifold learning algorithm. Journal of Vibration and Shock, Vol. 36, Issue 14, 2017, p. 111-115.
-
Wang Guangbin, Luo Jun, He Yilin Fault diagnosis of rotating machinery based on homogenized distance and supervised manifold learning. Mathematical Problems in Engineering, Vol. 10, 2015, p. 1-8.
About this article
Financial support from National Natural Science Foundation of China (51575178), financial support from Hunan Natural Science Foundation of China (2018JJ2120).
