Abstract
Constrained Independent Component Analysis (cICA) was developed from Independent Component Analysis (ICA), and the concepts and principles of independent component analysis still apply to constrained independent component analysis. This paper introduces the mathematical basis, basic principles and algorithms of constrained independent component analysis. Firstly, the mathematical basis of cICA is introduced. It mainly includes the entropy and negative entropy of irrelevant and whitening, Statistical opposition and multivariate Gaussian density random variables. Then the mathematical model of Constrained FastICA, the identifiability and uncertainty of the model, the FastICA independence criterion, FastICA optimization and preprocessing, FastICA algorithm and simulation examples are introduced. Finally, the shortcomings of fast independent component analysis and the advantages of constrained independent component analysis are analyzed. According to the establishment and evaluation indicators of signals, the basic principles and corresponding algorithms of constrained independent component analysis are introduced. The characteristics of the corresponding simulation show that the algorithm is effective in extracting signal characteristics.
1. Introduction
The issue of Independent Component Analysis (ICA) was proposed in the 1980s, although the name of the ICA was not adopted at the time. Common [1] proposed a blind source separation independent component analysis (ICA) method based on instantaneous aliasing signal analysis, and clarified the concept of ICA. A Kullbak-Leibler criterion is proposed as a comparison function, and a high-order approximation and comparison function based on the probability density function is used to measure the statistical independence of each component of the signal. In 1995, A. J. Bell and T. J. Sejnowski [2] analyzed the entropy of linear system maximizing output nonlinear nodes based on information theory, and obtained the criterion function of maximum information transmission.From this, an adaptive blind source separation and blind deconvolution method (informax) is derived which can recover the source signal from the mixed signal. The algorithm uses kurtosis as a measure function, which is very effective for separating speech signals (linear aliasing), but it is difficult to separate negative entropy signals. Constrained Independent Component Analysis (cICA) was originally proposed by Wei Lu and J. C. Rajapakse [3] applied it to EEG in 2000. In 2005, Wei Lu and J. C. Rajapakse [4] proposed a complete cICA algorithm framework. Since then, many literatures have studied it, and the literature [5-7] studied the cICA algorithm. The literature [8, 9] describes in detail how to establish a reference signal in the cICA algorithm, and points out the method and steps of establishing the reference signal and the importance of the reference signal in the cICA algorithm. In the field of application, cICA is mainly used in medical engineering, especially electrocardiogram, electroencephalogram and electrocardiogram. By combining independent component analysis with prior information in medical engineering, cICA improves the accuracy and effectiveness of independent component analysis. However, in the field of mechanical fault diagnosis, the application of constrained independent component analysis is relatively small.
In China, Professor He Zhenya from Southeast University [10] was the first scholar to start blind source separation research. He proposed a series of new criteria based on feature analysis and blind source separation and blind deconvolution of higher-order spectra, and achieved fruitful results. Some scholars in China have also followed suit, researching and innovating different blind source separation algorithms. They have achieved some results in software and hardware and have been developed in the fields of communication, speech and biomedicine [11].However, there are relatively few studies on constrained independent component analysis, the literature [12] points out that the theoretical development of cICA and proposed the development of ICA with reference signal, the application of ICA-R, including the selection of threshold parameters, the CompleteI ICA-R algorithm is a very flexible ICA algorithm compared to traditional ICA. The establishment of the reference signal and the influence of the parameters on the extraction of the sign signal are mainly described. In [13], constrained independent component analysis was applied to the separation of electroencephalogram (EEG) bit differences. The feasibility of this method was proved by simulation and corresponding engineering application research. Literature [14-16] respectively studied the cICA algorithm and cICA in the infrared point detection application.
2. FastICA algorithm and cICA algorithm
1) Introduction to FastICA algorithm.
Assuming a certain observable vector , let satisfy the ICA model , is an unknown mixture matrix, is the source signal. First of all, the raw data is preprocessed – whitened, resulting in a whitening signal , here is a whitening matrix, to meet the condition is 0, . FastICA algorithm is to find a separation matrix , make as independent as possible, here is the estimate of the source signal . For an independent component of the estimate , the negative entropy is maximized, that is non-Gaussian maximization. And must satisfy the condition is 1, then the optimal solution of is satisfied:
In the formula: is a constant, is the derivative of . The following fixed point iteration can be obtained:
must be normalized after each iteration, however, the convergence property of this formula is not obvious, because non-polynomial moments do not have the same good algebraic performance as real cumulants. So, the fixed point iteration adjusted as follows:
The next step is to normalize as a unit norm. For the calculation of coefficients in the formula, using Newton method.
According to Lagrange conditions, the extreme value of under the constraint 1 is obtained at the point where the gradient of the following Lagrange multiplier is zero:
The following Newton method to solve this equation, available approximate Newton’s iterative equation is:
This formula is the basic formula of fixed point iteration in FastICA algorithm.
2) Introduction of constrained independent component analysis algorithm.
It is known that , , …, are input mixed signals , , …, are the estimated source signals , , …, are reference signals. The partial prior information with the source signal is not exactly the same as the source signal. In the constrained independent component algorithm, the similarity measure between output signal and reference signal is added to the objective function of traditional ICA, so that only line vectors ( 1, 2, …, ) out of the desired signal source signal . If we use only one reference signal to find a row vector of , we get , it is the closest source to , which is called a unit of cICA. Constrained independent component analysis is based on the independent component analysis to add a constraint, the formation of constrained optimization problem, the basic model is:
The optimization objective function in the above formula is the contrast function of ICA. In the constrained independent component analysis (ICA), the expected independent components are extracted, and the number of independent components to be extracted can be flexibly selected. 0 is inequality constraint. The prior information of the extracted signal is added to the ICA algorithm to force the algorithm to converge to the desired independent component. 0 is the equality constraint, the independent components of the output are unitized.
The similarity between the definition output signal and the reference signal is denoted by , if there is one and only one independent component is close to the reference signal, the following relation can be obtained:
In the formula, is the separation vector corresponding to the independent component which is selected to separate, and ( 1, 2,…, ) is the separation vector corresponding to the other independent components. So, for the output only when , the following equation holds:
For the here is a threshold parameter, its value to meet the condition: . For the model Eq. (6) is a constrained optimization problem that can be solved by Lagrange multipliers.
3. Simulation experiment
1) Simulation experiment of FastICA algorithm.
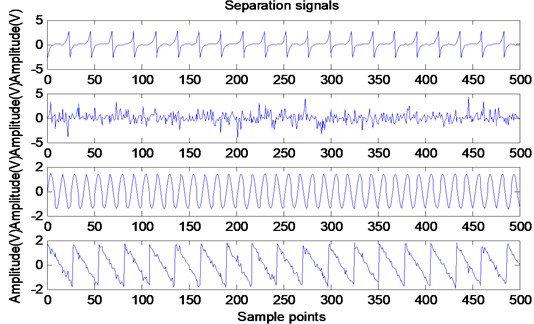
In order to further illustrate the application of ICA principles and algorithms, this section presents a set of simulation experiments. First, four independent non-Gaussian source signals are generated according to Eq. (9) as shown in Fig. 1:
where is a sine signal, is a funny curve, is sawtooth wave, is pulse noise signal, sampling point is 500. Now produce a random mixed matrix , Perform random mixing according to Eq. (3) to obtain observable time-domain waveforms as shown in Fig. 2. Perform the decomposition operation according to the FastICA algorithm described in Section 2.3.5. The resulting time-domain waveforms are shown in Fig. 3.
As can be seen in Fig. 1 and Fig. 3, although the signal is very complex, but after FastICA algorithm, the source signal has been better separation, separation accuracy is high, but the separation order and the signal amplitude has changed, this also validates two uncertainties in ICA decomposition: Separation order uncertainty and amplitude uncertainty. However, the waveforms of the separated signals are basically the same, that is, the waveform does not change in frequency domain, which does not affect the analysis and processing of signals. So, in the practical engineering application is allowed to accept such uncertainty.
Fig. 1Time waveforms of source signals
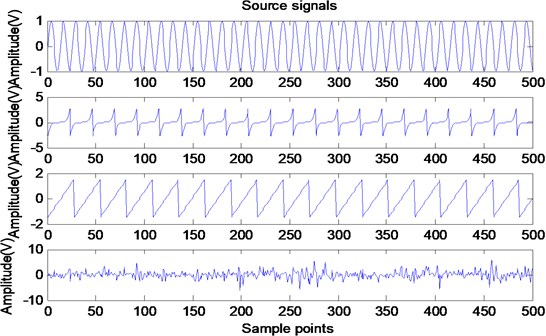
Fig. 2Time waveforms of mixing signals
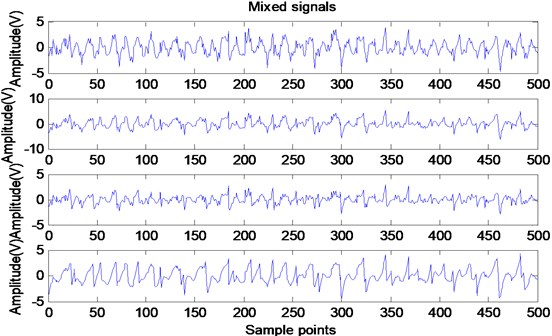
Fig. 3Time waveforms of separation signals
2) Simulation experiment of constrained independent component analysis.
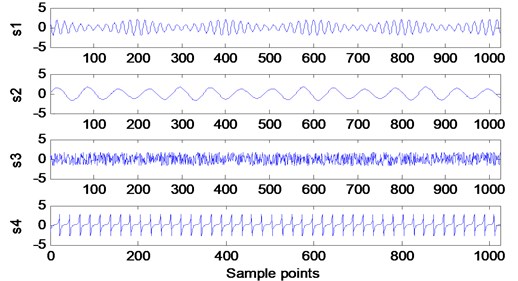
In order to further explain the basic principles of cICA and the application of the algorithm, this section gives a set of simulation experiments. First, four independent non-Gaussian source signals are generated according to Eq. (10) as shown in Fig. 4:
Here 550 Hz, 143 Hz, 50 Hz, 38 Hz, is the gear fault signal that the gearbox amplitude modulation and the frequency modulation work together. The carrier frequency is , the modulation frequency is . is a simple bearing modulation signal, the carrier frequency is , the modulation frequency is . is to generate random white noise sequence of points , is a funny curve. Through 10 kHz sampling frequency acquisition data, sampling points for the 5000, take the first 1024 data.
Fig. 4Time waveforms of source signals
Now a random mixing matrix is generated, which is randomly mixed according to Eq. (8). The resulting time-domain waveform is shown in Fig. 5.
In practice, the gearbox parameters and speed of the gearbox are known, so the meshing frequency can be calculated. According to the steps of the reference signal establishment and the method thereof, a rectangular square wave reference signal is established to make its period equal to the meshing frequency of the fault gear of the simulated gearbox, and the constraint independent component analysis is performed to extract the fault characteristic frequency. The obtained result is shown in Fig. 6. Fig. 6 shows the generated periodic square-wave sequence equal to the gear meshing frequency and the gear fault signature extracted as a reference signal.
Fig. 5Time waveforms of mixing signals
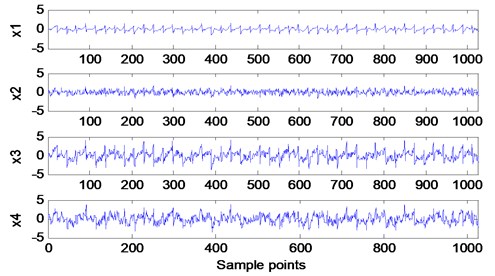
Fig. 6Time waveforms of the appropriate reference signal and the extracted y1
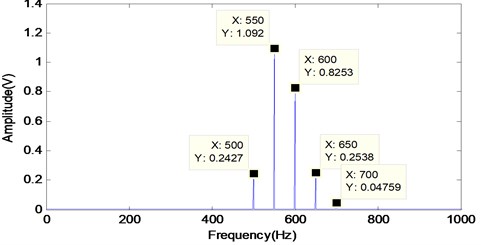
Amplitude spectrum analysis is performed on the extracted fault signatures, as shown in Fig. 7. Fig. 7 shows the amplitude spectrum of the extracted signal in Fig. 6. It can be seen from the figure that there is mainly a gear fault engagement frequency of 550 Hz, and there is a significant modulation side band with a modulation frequency of 50 Hz, which is the result of the joint effect of AM and FM. Therefore, the mixed signal can be correctly separated by cICA method to extract the fault signature signal.
Fig. 7Signal amplitude spectrum of the extracted y1
4. Conclusions
This paper compares the mathematical foundations of FastICA and cICA, and analyzes the shortcomings of fast independent component analysis and the advantages of constrained independent component analysis. Constrained Independent Component Analysis (cICA) was developed from Independent Component Analysis (ICA), and the concepts and principles of independent component analysis still apply to constrained independent component analysis. The corresponding simulation results show that the algorithm is effective in extracting signal characteristics. In practical engineering applications, cICA has a wide range of applications in the fields of mechanical fault diagnosis, image analysis and processing, and signal denoising.
References
-
Comon P. Independent component analysis, a new concept. Signal Processing, Vol. 36, 1994, p. 287-314.
-
Bell A. J., Sejnowski T. J. An information-maximization approach to blind separation and blind deconvolution. Neural Computation, Vol. 7, 1995, p. 1129-1159.
-
Lu W., Rajapakse J. C. Approach and applications of constrained ICA. IEEE Transactions on Neural Networks, Vol. 16, Issue 1, 2005, p. 203-212.
-
Lu W., Rajapakse J. C. ICA with reference. Neurocomputing, Vol. 69, 2006, p. 2244-2257.
-
Li C., Liao G., Shen Y. An improved method for independent component analysis with reference. Digital Signal Processing, Vol. 20, Issue 2, 2010, p. 575-580.
-
Sun Z.-L., Shang L. An improved constrained ICA with reference based unmixing matrix Initialization. Neurocomputing, Vol. 73, Issues 4-6, 2010, p. 1013-1017.
-
Ren D., Ye M. Extracting post-nonlinear signal with reference. Computers and Electrical Engineering, Vol. 37, Issue 6, 2011, p. 1171-1181.
-
Guoyu Liangyu, Wu Chuanhui Fault feature extraction of rolling bearings based on spectral kurtosis and cICA. Mechanical Strength, Vol. 5, 2013, p. 559-565.
-
Wang X., et al. Approaches and applications of semi-blind signal extraction for communication Signals based on constrained independent component analysis: The complex case. Neuro Computing, Vol. 101, 2013, p. 204-216.
-
Zhenya He Blind signal processing. International Academic Activities, Vol. 6, 1996, p. 15-17.
-
Wu Chuanhui, Guoyu Liangyu Fault feature extraction of rolling bearings based on cICA in speed change process of rotating machinery. Mechanical Science and Technology, Vol. 8, 2013, p. 1176-1181.
-
Mi Jianxun Independent Component Analysis Theory with Reference Signal and Its Application. University of Science and Technology of China, 2010.
-
Gao Ansheng, Luo Yangyu, et al. Constraint independent component analysis and its application to pseudo - differential separation of EEG signal. Biomedical Engineering Journal, Vol. 3, 2008, p. 497-501.
-
Zhang Shoucheng New CICA unit ICA-R fixed point algorithm. Computer Engineering and Applications, Vol. 36, 2011, p. 137-140.
-
Dingrui Caicheng, Shi Erke, et al. Infrared point target detection method based on cICA. Journal of Beijing Institute of Technology, Vol. 11, 2009, p. 1001-1005.
-
Wang Zhiyang, Du Wenliao, et al. Model based CICA and its application in fault diagnosis of rolling bearings. Vibration and Shock, Vol. 34, Issue 8, 2015, p. 66-70.
About this article
The authors are grateful for the funding of this work by the China Coal Industry Association Science and Technology Research Project (MTKJ2016-221), Henan Province Science and Technology Development Research Project Fund (17210221002), China Postdoctoral Science Foundation Funded Project (Project No. 2016M592289) and Henan Science Foundation Funded Project (U1504503).
