Abstract
In order to improve the accuracy of loop unrolling factor in the compiler, we propose a loop unrolling method based on improved random decision forest. First, we improve the traditional random decision forest through adding weight value. Second, BSC algorithm based on SMOTE algorithm is proposed to solve the problem of unbalanced data sets. Nearly 1000 loops are selected from several benchmarks, and features extracted from these loops constitute the training set of the loop unrolling factor prediction model. The model has a prediction accuracy of 81 % for the unrolling factor, and the existing Open64 compiler gives 36 % only.
1. Introduction
The compiler involves numerous optimization stages, known as “optimization pass”. The compiler will execute various optimization passes according to the original order of input program, so as to improve the program performance. Cost model commonly exits in various stages of the compiler to guide execution of optimization passes. For instance, at loop interchange stage, a cost model is needed to calculate whether loop interchange can obtain positive gains and what negative effects it will cause to the program, in order to make a decision on whether to conduct loop inter-change [1]. The performance of cost model directly influences the optimization ability of compiler, but even the cost model carefully designed by the compiler designer for a specific optimization stage after mature deliberation cannot necessarily reach the ideal optimization effect. For example, when the two loops in Fig. 1 are fused at the stage of loop fusion [2], the cost of loop iteration can be reduced, and the program performance is improved. Based on such consideration, most optimization compilers will choose the operation of loop fusion at this stage. But when compilation enters the stage of automatic vectorization [3], the previous optimization of loop fusion will hinder the process of vectorization, as the first loop can carry out vectorization, but the second loop cannot conduct vectorization due to the existence of true dependence. After the two loops are fused, the entire loop will be unable to conduct vectorization. But the gains of vectorization are obviously higher than the gains of loop fusion. Therefore, considered from the global view, loop jamming should not be conducted. Hence, it is hard for compiler designers to give an overall consideration, and provide an appropriate cost model for every optimization stage.
Fig. 1Influence of loop fusion on follow-up vectorization. The first loop shown in (a) can be vectorized and the second loop cannot be vectorized. The fused loop shown in (b) cannot be vectorized
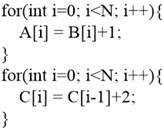
a)
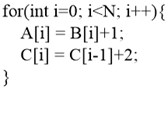
b)
This paper displays how to predict loop unrolling factors by utilizing and improving random decision forest technology. According to the experiment, it is demonstrated that the prediction accuracy of this model for optimal or sub-optimal loop unrolling factors reaches 81 %. The random forest model gained is tested via SPEC2006 test set, and the performance of some programs is improved by 12 % on average when compared with that of prediction model of the original compiler. Therefore, our method can effectively help the compiler improve the compiler optimization ability.
2. Overview of loop unrolling
As a frequently-used compiler optimization technique, the initiative motivation of loop unrolling is to reduce loop overheads. As shown in Fig. 2, loop unrolling aims to copy statements in the basic block of loop for multiple times, reduce loop iterations and loop branches, and conduct data prefetching better [4]. When loop un-rolling is combined with module scheduling, the initiation interval of fractional value can be realized [5]. For the current processor, major gains of loop unrolling include improvement of instruction-level parallelism, register locality, and hierarchical storage locality [6, 7]. Meanwhile, loop unrolling is also a necessary means to efficiently explore some hardware characteristics, such as exploring the opportunity of generating double instructions or offsetting the cost of a single prefetching instruction through several load/store instructions [8, 9]. But loop unrolling also has some defects. Inappropriate unrolling might bring about some negative gains to the program performance. For instance, loop unrolling might lower the hit rate of instruction cache, and trigger overflow of instruction buffer. Meanwhile, loop un-rolling might need extra intermediate variables, result in register spilling, increase memory access, and reduce the performance of the program.
Fig. 2Example of loop unrolling
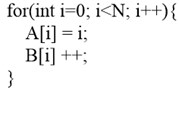
a)
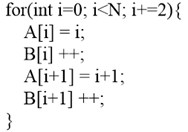
b)
Fig. 3Training and prediction process of random forest model
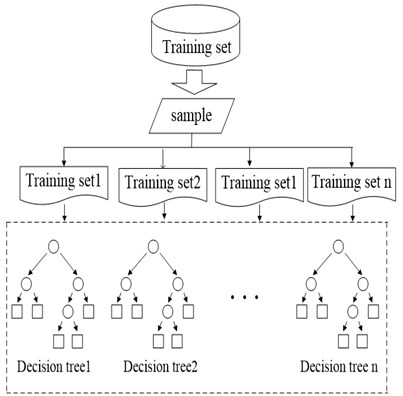
a) Decision forest training stage
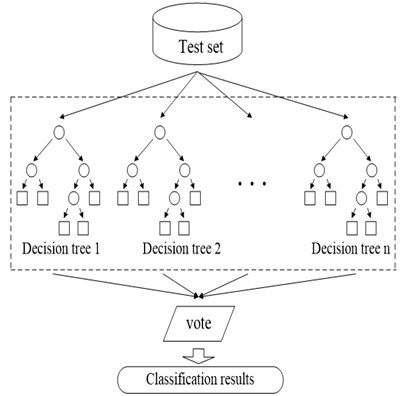
b) Decision forest prediction stage
3. Random decision forest model
3.1. Forest
Random decision forest is a classifier to train and predict samples by utilizing several decision trees [10]. At the training stage, the node of every decision tree is randomly selected from feature vectors of training samples, so the decision trees have a great difference, which can avoid over-fitting phenomenon. At the prediction stage, every decision tree can give a prediction result, and the random forest will comprehensively vote on these results, so as to give a final prediction result. Fig. 3. Training and prediction process of random forest model. Fig. 3(a) is the schematic diagram for the training stage of random forest. training sets are selected from the original training set, and decision tree is established for each training set. Fig. 3(b) is the schematic diagram for the prediction stage of random forest. The test sample is predicted with decision trees, to obtain prediction results. Then the final classification result is produced through voting on the results.
3.2. Algorithm improvement
Weighted random forest. Different features have different influences on the prediction results. Some features will produce a comparatively great influence on the result, while some features have a small effect on the result. For instance, according to the experience of compiler optimization, the number of statements in basic block of loop body is obviously a key factor that influences loop unrolling factors, while the number of reduction variables in basic block of loop body has a small influence on loop unrolling factors. Therefore, we propose decision tree empowerment and weighted voting for the traditional random forest. When weighted voting is adopted, a big influence will be produced on the classification effect of random forest. If the weighting is appropriate, the classification effect of random forest will be improved naturally. But if the weighting is inappropriate (for example, the weight of some decision trees is too high), the ultimate classifier will excessively rely on some decision trees, leading to over-fitting of data. Hence, the ultimate classification result is reduced. In this paper, the following calculation formula of decision tree weight is adopted:
In the above formula, means the weight of classifier , indicates the number of classifiers, represents the posterior probability of the classification result of classifier i. The greater the value of is, the greater the value of will be.
Fig. 4 presents the prediction algorithm for loop unrolling times via the improved random forest algorithm.
SMOTE algorithm improvement. Under the influence of computer hardware architecture design, the optimal loop unrolling factor is often the integer power of 2, such as 1, 2, 4, and 8, and the possibility for the optimal unrolling factor not to be the integer power of 2, such as 3, 5, 6, and 7, is quite small. As a result, the classification problem in this paper belongs to unbalanced dataset classification problem. SMOTE algorithm core idea is to establish reasonable negative samples, making the number of negative samples equivalent to the number of positive samples. Thus, unbalanced dataset is avoided to some extent. However, the SMOTE algorithm has certain blindness in constructing negative samples, and the constructed negative samples tend to get closer and closer to the positive samples. An improved SMOTE algorithm, known as BCS algorithm is proposed in this paper. The core idea of BCS algorithm is: when “artificial sample” is established for the negative type, it should be made to approach the center of the negative to the greatest extent, and keep away from the edges of positive and negative types. The specific implementation steps are as follows:
Step 1: Calculate the average value of negative samples as the center of negative samples. Record the negative sample set as:
and the center of negative samples is .
Step 2: Generate the artificial sample set:
Via SMOTE algorithm, to make the sum of number of elements in negative sample set and number of elements in artificial sample set greater than the number of elements in positive sample set.
Step 3: Transform the artificial sample generated via SMOTE algorithm in Step 2. The formula is: . Hence, a new artificial sample set is produced.
Step 4: Add the new artificial sample set into the original negative sample set, re-calculate the average value, and delete some samples comparatively far from the center in the set via under-sampling method, to make the number of elements in negative sample set equivalent to the number of elements in positive sample set. Ultimately, the overall training set is formed.
Fig. 4Improved random forest voting algorithm

4. Loop unrolling method based on random forest
The establishment and features selection of training set include three steps:
Step 1: Extract nearly 1000 loops to form machine learning training examples from 16 test sets including SPEC CPU 2006, NPB benchmarks and so on.
Step 2: Conduct loop unrolling for every training example for 1 to 8 times, test the corresponding execution time respectively, and determine the optimal unrolling factor of every example. The optimal unrolling factors of all examples are shown in Fig. 5. Among them, the examples with the optimal unrolling factor of 1, 2, 4 and 8 occupy 84 % of all examples, consistent with the traditional compiler optimization experience. The probability for the optimal unrolling factor to be 8 is 11 times higher than the probability for the optimal unrolling factor to be 3.
Fig. 5Statistics about optimal unrolling factors of test examples
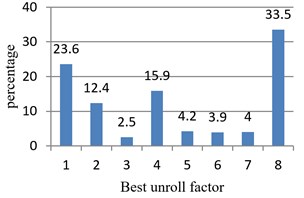
Table 1Loop features
Loop characteristics | Loop characteristics |
Language (C/Fortran) | Number of jump statements |
Iterations | Number of variables in the loop |
Maximum iterative dependency length of loop | Number of variables outside the loop |
Average iterative dependency length of loop | Number of variables used in the loop |
Indirect array access and storage times | Number of variables defined in the loop |
Number of protocol variables | Memory operation times |
Function call times | Number of variables defined in and used outside the loop |
Number of floating-point variables | Number of variables defined outside and used in the loop |
Step 3: Establish sample features for each loop, expressed with vector . indicates the features vector, which includes loop features such as loop iterations and number of statements in the loop body. It is collected by the compiler in the process of compiler optimization, and the specific features are presented in Table 1. represents the optimal unrolling factor, limited to 1-8. 1 means that no loop un-rolling is conducted.
5. Experiment and analysis
5.1. Experimental platform
The Sunway platform is adopted as the test platform, Redhat Enterprise 5 is used as the operating system. The main frequency of CPU is 2.0 GHz, the memory size is 2 GB. Open source modern structure optimization compiler Open64 is used as the compiler.
5.2. Result analysis
Table 2 shows the prediction probability of several loop unrolling cost models for unrolling factors. Among them, “Open64” indicates the built-in loop unrolling cost model of Open64 compiler, “traditional random forest” means to conduct prediction for unrolling factors via random forest model not improved. “weighted random forest” means to improve the traditional random forest through weighting, as proposed in this paper. “weight-balanced random forest A” means to improve the “weighted random forest” by utilizing SMOTE algorithm to solve the unbalanced dataset problem. “weight-balanced random forest B” means to improve the “weighted random forest” by utilizing BCS algorithm to solve the unbalanced dataset problem, i.e. the ultimate scheme proposed in this paper. For instance, as for the prediction result of traditional random forest algorithm, the probability for sub-optimal unrolling factors is 0.14. The ratio of program execution efficiency and cost of theoretical optimal unrolling factor is 1.06x.
It can be seen from Table 2 that the traditional random forest and improved random forest methods are much better than the built-in cost model of Open64 in pre-diction for loop unrolling factors. Open64 can give the optimal or sub-optimal un-rolling factor under 36 % only. The traditional random forest can predict the optimal or sub-optimal unrolling factor under 72 %. After weighting improvement is con-ducted, the prediction accuracy reaches 75 %. If the SMOTE algorithm is used to solve the unbalanced dataset problem on such basis, the accuracy can reach 79 %. If BCS algorithm proposed in this paper is used to solve the unbalanced dataset problem, the accuracy can reach 81 %. The above experimental data demonstrate that the weight-balanced random forest model proposed in this paper can accurately predict loop unrolling factors.
Table 2Prediction results of five models for unrolling factors
Prediction result | Open64 | Traditional random forest | Weighted random forest | Weight-balanced random forest A | Weight-balanced random forest B | Average cost |
Optimal unrolling factor | 0.16 | 0.58 | 0.60 | 0.64 | 0.65 | 1x |
Sub-optimal unrolling factor | 0.20 | 0.14 | 0.15 | 0.15 | 0.16 | 1.06x |
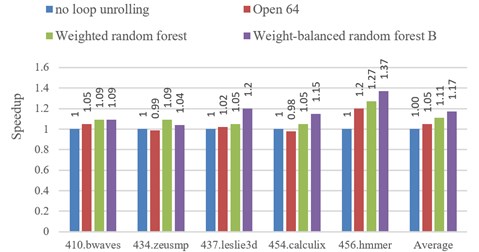
When the built-in loop unrolling cost model of Open64 and weighted random forest model of our paper are used to compile some programs of SPEC2006. The speed-up of program execution is displayed in Fig. 6. When the built-in loop unrolling model of Open64 is utilized, the program performance is improved by 5 % on aver-age. When the loop unrolling method of this paper is used, the program performance is improved by 12 % on average.
Fig. 6Comparison about the execution effects of some SPEC CPU 2006 programs
6. Conclusions
In this paper, a method to improve the loop unrolling optimization ability of compiler via machine learning model is proposed. Firstly, the traditional random forest model is improved through weighting and unbalanced dataset processing. Secondly, the training set is established to train the model. According to the experiment, the model after training can give the optimal or sub-optimal unrolling factor under 81%. Besides, it is tested via some SPEC2006 test sets. The built-in loop un-rolling model of Open64 can improve the program performance by 5% only, while the method of predicting loop unrolling factors via weight-balanced decision forest proposed in this paper can improve the program performance by 12% on average. The programs will be compiled through hundreds of optimization passes to get efficient object code, and the existing compiler performs fixed optimization passes over all target programs. However, different programs need different optimization passes. For future work, we expect to apply machine learning algorithms to construct program optimization passes selection model.
References
-
Pouchet L. N., Bondhugula, Bastoul, et al. C. Loop transformations: convexity, pruning and optimization. Proceedings of POPL, 2011, p. 549-562.
-
Mehta S., Lin P. H., Yew P. C. Revisiting loop fusion in the polyhedral framework. Proceedings of PPOPP, 2014, p. 233-246.
-
Gao W., Zhao R. C., Han L., et al. Research on SIMD auto-vectorization compiling optimization. Journal of Software, Vol. 26, Issue 6, 2015, p. 1265-1284.
-
Jha S., He B., Lu M., et al. Improving main memory hash joins on Intel Xeon Phi processors: an experimental approach. Proceedings of the VLDB Endowment, Vol. 8, Issue 6, 2015, p. 642-653.
-
Arslan M. A., Gruian F., Kuchcinski K. A. Comparative study of scheduling techniques for multimedia applications on SIMD pipelines. Proceedings of HIS, 2015, p. 3-9.
-
Sengupta A., Mishra V. K. Swarm intelligence driven simultaneous adaptive exploration of datapath and loop unrolling factor during area-performance tradeoff. Proceedings of ISVLSI, 2014, p. 106-111.
-
So W., Dean A. G. Software thread integration for instruction-level parallelism. ACM Transactions on Embedded Computing Systems, Vol. 13, Issue 1, 2013, p. 1-23.
-
Cortes K. E., Goodman J., Nomi T. Intensive math instruction and educational attainment long-run impacts of double-dose algebra. Journal of Human Resources, Vol. 50, Issue 1, 2014, p. 108-158.
-
Domagała Ł., Amstel D. V., Amstel F., Sadayappan P. Register allocation and promotion through combined instruction scheduling and loop unrolling. Proceedings of CC, 2016, p. 143-151.
-
Tantithamthavorn C., Mcintosh S., et al. Automated parameter optimization of classification techniques for defect prediction models. Proceedings of ICSE, 2016, p. 321-332.
