Abstract
A kind of self-tuning vibration absorber is presented. The relationship between the installation position and the vibration damping effect of the self-tuning vibration absorber is established, the influence on the damping effect is discussed. Then, on the vibration test bed, the theoretical analysis results are tested and verified. The results show that, installation position of the self-tuning vibration absorber has a significant influence on its vibration damping effect. When installed near the source location, the self-tuning vibration absorber has a better vibration damping effect. It is should be avoided in the area of vibration deterioration.
1. Introduction
By transferring the vibration energy of the main system to the dynamic vibration absorber, ideal damping effect can be achieved when the natural frequency and the excitation frequency are the same [1, 2]. The self-tuning vibration absorber can turn natural frequency automatically to adjust to the frequency of the excitation source. It is always in the tuning state to adaptively vibration absorption. Which are often the most reliable engineering solution having many advantages such as wide tuning frequency band and stability. The existing research focuses on control methods and new materials [3-7].
While, the vibration equipment is often flexibly installed on the basis with vibration isolators and have multiple vibration modes. Which cause vibration coupling in different vibration modes [6]. The installation position has a significant effect on the damping effect of the self-tuning vibration absorber.
In this paper, a self-tuning vibration absorber is presented, and the relationship between the installation position and the vibration damping effect is established, and a series of useful conclusions are obtained. It can provide guidance and reference for the engineering application of self-tuning vibration absorber.
2. Self-tuning vibration absorber
The self-tuning vibration absorber presented here is shown in Fig. 1. Four rectangular springs form the articulated composite beam structure, and the span in the vertical direction can be modulated by the linear motor moving up and down, denoted as .
For the composite beam structure, refers to XU, the natural frequency is:
3. Theoretical analysis of vibration damping characteristics
The damping system consisting of a self-tuning vibration absorber and a two degrees of freedom vibration damping object is shown in Fig. 2.
Fig. 1Self-tuning vibration absorber

Fig. 2Mechanical model of vibration damping system
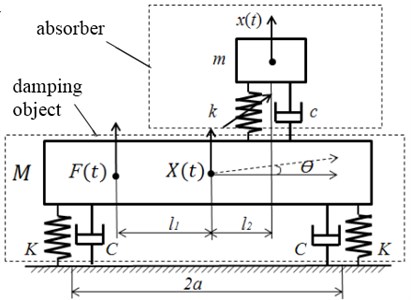
Exciting force is , the position of exciting point is , the installation position of self-tuning absorber is variable. The motion equation of vibration damping system can be obtained according to the coordinate system set up in Fig. 2:
In which:
Do the Fourier transform to Eq. (2):
The impedance matrix of the vibration damping system is:
where:
The solution for Eq. (4) is:
where:
The vibration energy of the vibration damping object is:
When the vibration absorber is not installed, the vibration energy of the vibration damping object is:
The damping effect of the self-tuning vibration absorber is:
4. The effect of the installation position
The damping effect of the self-tuning vibration absorber is a function of the installation position of the absorber obtained by the Eq. (12). To simplify the analysis, ignore the damping of damping system, the natural frequency of the original vibration object in the vertical direction and roll direction are and :
The damping effect of the self-tuning vibration absorber is:
According to the Eq. (15), the function of the damping effect , the frequency of the exciting force and the installation position of the self-tuning vibration absorber can be obtained.
When:
While , only if 0, combined with Eq. (15):
where , , has real solutions between (when ) or (when ). That is, the frequency, at which the vibration of the vibration damping object is deteriorated, is between the natural frequencies and :
In Eq. (19), the position that causes vibration deterioration is only related to the parameters of the damping object itself. This is its inherent property and has nothing to do with the parameters of the absorber. This is an inherent property that has nothing to do with the parameters of the absorber.
According to the Eq. (15), when the installation position of the self-tuning vibration absorber is the same as the position of the exciting force, that is, , the damping effect is optimized.
When , the relationship between the damping effect of the self-tuning vibration absorber and its installation position is shown in Fig. 3(a) is a three-dimensional graph, and Fig. 3(b) is a contour map.
In Fig. 3, There is an area of vibration deterioration Between the modal frequencies of , . When installed at the location of vibration source , a better damping effect can be achieved. While, the same situation occurs in the case of .
Therefore, self-tuning vibration absorber should be installed at the location of vibration source if possible. And the mentioned areas of vibration deterioration should be avoided.
Fig. 3damping effects of self-tuning vibration absorber under condition of ωv<ωt
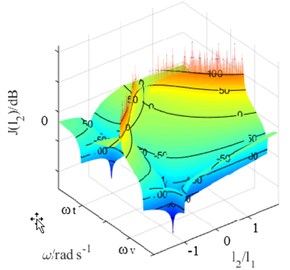
a)
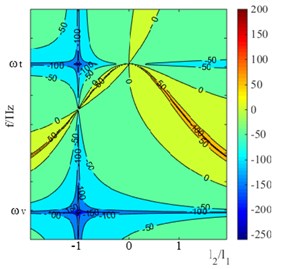
b)
5. Experimental research
A vibration damping test system is shown in Fig. 4 to verify the above analysis results.
The installation position of the absorber can be varied along the damping object. Four acceleration sensors are set on the damping object:
where is the th acceleration signal of the damping system without absorber, and th acceleration signal of the damping system with absorber. The damping effect of the absorber of different installation positions are shown as follows.
Fig. 4Multi-DOF Test Bench System: 1 – Signal collector, 2 – Computer, 3 – Signal generator, 4 – Self-tuning vibration absorber, 5 – Damping object, 6 – Acceleration sensor, 7 – Control box, 8 – Exciter, 9 – Power amplifier

Fig. 5Damping effects of different installation location under 25Hz sinusoidal excitation
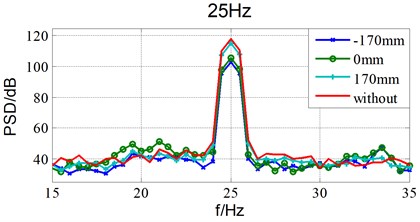
Fig. 6Damping effects of different installation location under 50Hz sinusoidal excitation
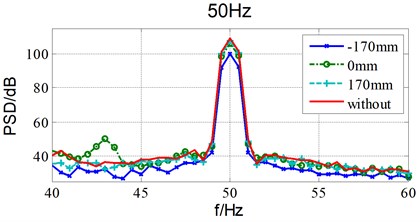
Table 1Damping effects of different installation location of self-tuning vibration absorber
– | –170 mm | 0 mm | 170 mm |
25 Hz | 14.8 dB | 3.4 dB | 2.7 dB |
50 Hz | 9.2 dB | 2.9 dB | 1.1 dB |
According to Table 1, the damping effect can be 14.8 dB/9.2 dB at 25 Hz /50 Hz when installed at the source position. The damping effect is much better than that of other locations. Which validate the theoretical analysis results.
6. Conclusions
In this paper, a new kind of self-tuning dynamic absorber is presented. The relationship between the installation position and the vibration damping effect of the self - tuning vibration absorber is discussed theoretically and numerically. It shows that there has an area of vibration deterioration between the modal frequencies of the damping object. When installed at the location of vibration source, a better damping effect can be achieved.
On the multi-DOF test bench system, the theoretical analysis results are validated experimentally. The results show that the damping effect are 14.8 dB/9.2 dB at 25 Hz/50 Hz when installed at the source position. Which are much better than that of other locations.
References
-
Hou Jiuxiao, Zhu Haichao. Double-DOF self-tuning vibration absorber and its vibration absorbing characteristics. Noise and Vibration Control, Vol. 35, Issue 6, 2015, p. 36-40.
-
Sun J. Q., Jolly M. R., Norris M. A. Passive, adaptive and active tuned vibration absorbers – a survey. Journal of Vibration and Acoustics, Vol. 117, Issue 117, 1995, p. 234-242.
-
Pipitone G., Barone G., Palmeri A. Optimal design of double-skin façades as vibration absorbers. Structural Control and Health Monitoring, Vol. 47, Issue 5, 2018, p. 1329-1351.
-
Hu Y., Chen M. Z. Q., Xu S., et al. Semiactive inerter and its application in adaptive tuned vibration absorbers. IEEE Transactions on Control Systems Technology, Vol. 25, Issue 1, 2016, p. 294-300.
-
Patil S. S., Awasare P. J. Vibration isolation of lumped masses supported on beam by imposing nodes using multiple vibration absorbers. Mechanical Engineering Research, Vol. 6, Issue 1, 2016, p. 88-95.
-
Xu Zhenbang, Xinglong Gong, Chen Xianmin. Mechanical vibration absorber with tunable resonant frequency and its vibration attenuation characteristics. Journal of Vibration and Shock, Vol. 29, Issue 2, 2010, p. 1-7.
