Abstract
Elastic cylindrical shells interacting with a viscous incompressible fluid are widely used in various branches of science and technology, such as engineering and aviation engineering. They provide the possibility for solving a lot of problems, such as: reducing constructing weight and dimensions, equalizing dynamic influences and vibration level, as well as reducing friction and wearing, cooling. Mathematical model of the system, representing three coaxial cylindrical shells, freely supported at the ends, and interacting with viscous incompressible fluid between them under mechanical system harmonic vibration is constructed. This mathematical model represents a coupled system consisting of the Navier-Stokes, continuity for each fluid and equations and the ones of elastic coaxial cylindrical shells dynamics which are based on the Kirchhoff-Love hypotheses and the corresponding boundary conditions, namely: for the fluid non-flow and for free attaching for the shells. The constructed mathematical model allows to investigate the oscillations of a mechanical system consisting of coaxial elastic cylindrical shells interacting with viscous incompressible liquids in order to identify dangerous operating modes.
1. Introduction
Coaxial elastic thin-walled shells interacting with viscous incompressible fluid between them are of great significance for the development of modern high-tech products that are used in rocket, space and automobile industry, railway transport, agricultural machinery, fuel and energy complexes. They provide the possibility for solving a lot of problems, such as: reducing constructing weight and dimensions, equalizing dynamic influences and vibration level, as well as reducing friction and wearing, cooling. The investigation of thin-walled structures dynamics was made in references [1, 2]. Viscous incompressible fluid interaction with elastic plates is considered in references [3-7]. Geometrically nonlinear oscillations of circular cylindrical shells under internal fluid flow activity were investigated in references [8, 9]. In this case, the shell is modeled on the basis of Donnell's nonlinear theory of the shell, keeping geometric imperfections in the inertia plane. Experimental and theoretical parametric study is carried out to investigate transmural pressure effect of on the nonlinear dynamics and stability of circular cylindrical shells, there ends are fixed and loaded with internal fluid flow [10]. Cavitation effects in vibrations based on a model experimental setup for the study of fast flowing hydrodynamic processes with allowance for the interaction of liquid, gas, and deformable structure are investigated in [11]. A variant of a three-dimensional mathematical formulation and a numerical implementation algorithm is designed to determine the dynamic characteristics of arbitrary geometry shells. They are completely or partially filled with a compressible inviscous fluid and are considered in [12]. The analysis of circular cylindrical shells panel flutter with ideal compressible fluid and a streamlined supersonic gas flow is carried out [13]. Mathematical model of this system consisting of partial differential equations and describing viscous incompressible fluid dynamics and an elastic ribbed shell is presented in [14, 15]. References [16, 17] present the solution annular cross section hydroelasticity problem, consisting of viscous incompressible fluid dynamics equations and the ones of internal and external elastic cylindrical shells of finite length dynamics, the letter being based on the Kirchhoff-Love hypotheses with the corresponding boundary conditions under base vibration with a fixed the annular tube. No one’s is investigating the problem hydroelasticity of three elastic coaxial shells interacting with viscous incompressible fluids between them under vibration. In this paper, we consider the construction of a mathematical model that will provide a joint consideration of the vibration of a mechanical system, the inertia of the motion of a viscous fluid, and the elasticity of three cylindrical shells of finite length freely supported at the ends of the mechanical system.
2. Statement of the problem
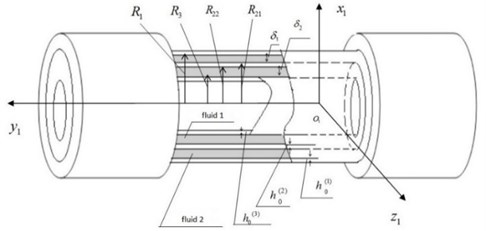
We consider the following mechanical model (Fig. 1), consisting of outer shell 1, middle shell 2 and inner shell 3, which are elastic coaxial cylindrical ones. The inner radius of the outer shell is denoted as , and the outer radius of the inner shell is , and the outer and inner radius of the middle shell are and , respectively. Fastening of the inner, middle and outer shells ensures their free support. The viscous incompressible fluid 1 and fluid 2 completely fills the gap between the walls of the three shells. We assume that the radial clearance of a cylindrical gap in the cylinder 1 is much smaller than the outer radius of the middle shell 2, that is, . We also assume that the radial clearance of a cylindrical gap in the cylinder 2 is much smaller than the inner radius of the middle shell 2, that is, . The mechanical system is influenced by the time-harmonic inertial force of moving space. The shifts of the inner and middle shells relative to the outer one at the ends is absent. Also, there is no inner and middle shells shifts relative to each other. The mechanical system is considered to be thermally stabilized.
Fig. 1Mechanical model
3. The theory and solution
To construct a mathematical model of the mechanical system under consideration, we introduce the coordinate system associated with the base to which the mechanical system is attached, that is, the center is located in the geometric center of the coaxial shells in the unperturbed state. We assume that the component of vibration acceleration along the axis is absent. We denote the vibration acceleration of the base by , . In addition, we introduce a cylindrical coordinate system , , (, , – the unit of the cylindrical system), which poles and the axes directions , coincide the cylindrical and Cartesian coordinate systems. (Fig. 2)
The mathematical model of the presented mechanical system has the form.
Equation of Navier-Stocks [18]:
and boundary conditions for cylindrical axes on impenetrable surface of shells in a cylindrical clearance are:
and also, the dynamic equations of elastic shell based on Kirchhoff-Love hypotheses are:
and boundary conditions of shells free attaching are:
where – pressure fluid 1; – pressure fluid 2; – fluid 1 density; – fluid 2 density; – kinematic viscosity of the fluid 1; – kinematic viscosity of the fluid 2; – Laplace operator; – Hamiltonian operator; – absolute fluid 1 volume unit acceleration; – absolute fluid 2 volume unit acceleration; – base drag acceleration; – the radius vector of the liquid particle mass center with respect to the pole of the cylindrical coordinate system , , ; – fluid 1 velocity of the relative to the cylindrical slot in the projections on the axis , , ; – fluid 2 velocity of the relative to the cylindrical slot in the projections on the axis , , ; , , – cylindrical coordinate system , , base unit; – elastic longitudinal shell shift which is positive in the direction , opposite in the direction ; – circumferential elastic movement in the direction , – shell sagging which is positive in the direction , coinciding with and opposite in a direction to a curvature center; – vector of elastic movements of shells; – Young’s modulus, – Poisson's ratio, – material density, – middle surface radius, – shell thickness, , , – projection of shells middle surface unit area the absolute acceleration; , 1, 2, 3 at axes , , 1 – outer shell, 2 – middle shell; 3 – inner shell:
4. Conclusions
Thus, we constructed a mathematical model of a mechanical system consisting of three coaxial elastic cylindrical shells interacting through viscous incompressible fluid layers under of in the presence of external vibration. The mathematical model of the system under consideration: shell-liquid-shell-liquid-shell is a connected system of equations, including non-linear partial Navier-Stokes equations and the continuity equation for describing the fluids dynamics of between elastic cylindrical shells, and partial differential ones for describing elastic cylindrical shells dynamics, based on Kirchhoff-Love hypotheses and the corresponding boundary conditions. The constructed mathematical model allows to investigate the oscillations of a mechanical system consisting of coaxial elastic cylindrical shells interacting with viscous incompressible liquids in order to identify dangerous operating modes.
Calculations have shown (Table 1) that the liquid pressure can really drop below 0.2 atmospheres at the resonance frequencies of the deflection of one of the shells, which corresponds to the conditions of cavitation.
Table 1Liquid pressure dω at the resonance frequencies of the middle shell
, rad/s | 6669 | 22225 | 64491 | 79909 | 110630 | 114836 |
, Pa | 9,90E+03 | 1,20E+09 | 1,49E+04 | 1,09E+05 | 4,95E+05 | 1,66E+05 |
References
-
Indeitsev D. A., Polypanov I. S., Sokolov S. K. Calculation of cavitation life-time of ship engine liner. Problemy Mashinostraeniya i Nadezhnos’ti Mashin, Vol. 4, 1994, p. 59-64, (in Russian).
-
Panovko Y. G., Gubanova I. I. Stability and Oscillations of Elastic Systems. Consultants Bureau Enterprises, Inc., New York, 1965.
-
Ageev R. V., Mogilevich L. I., Popov V. S. Vibrations of the walls of a slot channel with a viscous fluid formed by three-layer and solid disks. Journal of Machinery Manufacture and Reliability, Vol. 43, Issue 1, 2014, p. 1-8, https://doi.org/10.3103/S1052618814010026
-
Popov et al. V. S. Mathematical model of three-layer plate interaction with viscous incompressible liquid layer under foundation vibration. Applied Mathematical Sciences, Vol. 9, Issue 112, 2015, p. 5551-5559, https://doi.org/10.12988/ams.2015.57482
-
Mogilevich L. I., Popov V. S., Popova A. A. Interaction dynamics of pulsating viscous liquid with the walls of the conduit on an elastic foundation. Journal of Machinery Manufacture and Reliability, Vol. 46, Issue 1, 2017, p. 12-19, https://doi.org/10.3103/S1052618817010113
-
Starovoitov E. I., Leonenko D. V. Thermal impact on a circular sandwich plate on an elastic foundation. Mechanics of Solids, Vol. 47, Issue 1, 2012, p. 111-118, https://doi.org/10.3103/S0025654412010116
-
Popov V. S., et al. Mathematical model of movement of a pulsing layer of viscous liquid in the channel with an elastic wall. PNRPU Mechanics Bulletin, Vol. 3, 2014, p. 17-35, https://doi.org/10.15593/perm.mech/2014.3.02
-
Amabili M., Païdoussis M. P. Review of studies on geometrically nonlinear vibrations and dynamics of circular cylindrical shells and panels, with and without fluid-structure interaction. Applied Mechanics Reviews, Vol. 56, 2003, p. 349-381.
-
Amabili M., Pellicano F., Païdoussis M. P. Nonlinear dynamics and stability of circular cylindrical shells containing flowing fluid. Part III: truncation effect without flow and experiments. Journal of Sound and Vibration, Vol. 237, 2000, p. 617-640.
-
Karagiozis K. N., Païdoussis M. P., Misra A. K. Transmural pressure effects on the stability of clamped cylindrical shells subjected to internal fluid flow: theory and experiments. International Journal of Non-Linear Mechanics, Vol. 42, Issue 1, 2007, p. 13-23.
-
Gaynutdinova D. F. Development of technique of physical experiments to study interaction in the dynamic system liquid – design. PNRPU Aerospace Engineering Bulletin, Vol. 47, 2016, p. 215-229, https://doi.org/10.15593/2224-9982/2016.47.12
-
Bochkarev S. A., Lekomtsev S. V., Matveenko V. P. Numerical modeling of spatial vibrations of cylindrical shells partially filled by liquid. Computational Technologists, Vol. 18, Issue 2, 2013, p. 12-24.
-
Bochkarev S. A., Lekomtsev S. V. An aeroelastic stability of the circular cylindrical shells containing a owing uid. Vestnik Samara State Technical University, Series: Fiziko-Matematicheskie Nauki, Vol. 19, Issue 4, 2015, p. 750-767, https://doi.org/10.14498/vsgtu1453.
-
Kondratov D. V., Kondratova Y. N., Popov V. S., Plaksina I. V. The problem of a hydroelasticity for a tube ring-type a profile with elastic, geometrically irregular outer shell at pressure influence. Izvestiya of Saratov University, Series: Mathematics, Mechanics, Informatics, Vol. 13, Issue 3, 2013, p. 70-76.
-
Kalinina A. V., Kondratov D. V., Mogilevich L. I., Popova A. A., Kondratova Y. N. Mathematical Model of elastic ribbed shell dynamics interaction with viscous liquid under vibration. Vibroengineering Procedia, Vol. 8, 2016, p. 300-305.
-
Kondratov D. V., Kondratova J. N., Mogilevich L. I. Oscillating laminar fluid flow in a cylindrical elastic pipe of annular cross-section. Fluid Dynamics. Vol. 44, Issue 2009, 4, p. 528-539.
-
Kondratov D. V., Kondratova J. N., Mogilevich L. I. Studies of the amplitude frequency characteristics of oscillations of the tube elastic walls of a circular profile during pulsed motion of a viscous fluid under the conditions of rigid jamming on the butt-ends. Journal of Machinery Manufacture and Reliability, Vol. 38, Issue 3, 2009, p. 229-234.
-
Loitsyanskii L. G. Mechanics of Liquids and Gases, Pergamon Press, Oxford, 1966.
About this article
The study was funded by Russian Foundation for Basic Research (RFBR) according to the Project No. 16-01-00175-a and President of Russian Federation Grant MD-756.2018.8.
