Abstract
The study presented in this manuscript deals with a non-contact structural health monitoring approach based on the use of smartphone and computer vision algorithm to estimate the vibrating characteristics of a cantilever slender beam. We hypothesize that the vibration of the beam can be captured using a smartphone in slow-motion modality and the natural frequency of the beam can be extracted using a computer vision algorithm. The results show an excellent agreement between the conventional contact method and the non-contact novel approach proposed here.
1. Introduction
In the present paper, we propose an alternative approach based on structural dynamics and the non-contact detection of vibration modes using a smartphone camera in slow motion mode. The approach promises to replace some structural health monitoring approaches currently based on the non-contact measurement of dynamic parameters by means of sophisticated laser vibrometers [1, 2] or more conventional accelerometers. The adoption of high-speed cameras is being eased by cost-reduction and by the rapid developments in image processing. Some recent studies demonstrated that high-speed cameras can capture the modal characteristics of some structures using advanced image processing techniques [3-13]. Some of these works mostly use phase-based video motion processing algorithm [11, 14] and video motion magnification technique [3-8, 11-13]. These image processing algorithms need to know the frequency range as an input to identify the modal shapes and corresponding frequencies. Lately, this algorithm has been modified in order to achieve blind identification process [13, 15]. This technique analyzes the frames of any video with a multi-scale image processing method to extract the local pixel phases in order to get the local structural vibrations by using spatiotemporal filters applied as in the phase-based algorithm. All of these image processing algorithms require complex image transformations and may be computationally expensive. In addition, they work better with high-end cameras that provide high contrast images.
A viable alternative is provided by the multi-threshold technique [16] in which a small number of pixels within a pre-defined region of interest (ROI) is used to identify the vibration characteristics of a given structure. The method tracks subpixel movements of objects in a video scene and obtains the main frequency of vibration of the objects. The algorithm is based on the analysis of the luminance variation between two consecutive frames of the sequence. Therefore, no initial guess about the object shape or the movement frequency is needed [16]. In the study presented in this paper, we implemented this technique with MATLAB [17] to extract the natural frequency of a stainless-steel cantilever beam.
The novelty of the present paper is quite significant to validate the local multi-threshold video processing method in practical use to determine the natural frequency of the civil engineering structures. In this study, our aim is to investigate the natural frequency of a cantilever slender steel beam using a smartphone camera. In contrast to existing studies in the literature [8, 10-12, 15, 19], which use high cost, high fps camera to identify the vibration characteristics, we used only mobile phone camera to show that mobile phone camera can be used as a visual vibrometer by using specific video processing algorithm.
2. Experimental setup
We tested 41.34 mm×10.12 mm×1402 mm and made of Type 416 steel beam in the experiments. We try to define the vibration characteristics of this cantilever slender beam with using smartphone camera. The mechanical and the geometric properties of the specimens are listed in Table 1. Experiment setup consists of test beam with attached PCB 356B08 type accelerometer on the top of the beam as seen in Fig. 1. The smartphone is attached to the tripod as a fixed condition to decrease the noise in the video recordings. Test beam was excited by hammer and the motion was recorded by oscilloscope and smartphone to validate the results.
Fig. 1Photo of the experimental setup

The local multi-threshold technique [16] was applied to extract the natural frequencies of vibration of the beam. The ROI shown in Fig. 2 was considered and consisted of a squared frame made of 15×15 pixels. The pixel size was 1.4 µm. The maximum and minimum luminance in the area was determined and a total of 8 thresholds have been applied thus producing 8 binarized sequences. A temporal signal was obtained for each sequence and the Fourier transform of each signal was computed. By averaging the frequencies obtained from the 8 thresholder levels, the main frequency peak of the vibrating beam in the considered ROI was obtained. The Samsung Note 8 Smartphone was used in this experiment and it can enable recording videos at 240 fps with 720p resolution.
Fig. 2Cantilever steel beam and frame example with ROI


Table 1Geometric and mechanical properties of the beam tested in this study
Material | 416 steel |
Length (mm) | 1402 |
Free length (mm) | 1207 |
Cross-section (mm2) | 10.12×41.34 |
Young’s modulus (GPa) | 200 |
Density (kg/m3) | 7750 |
Poisson’s ratio | 0.28 |
Yield stress (MPa) | 276 |
The coefficient of thermal expansion (m/m°C) | 9.9×10-6 |
3. Results
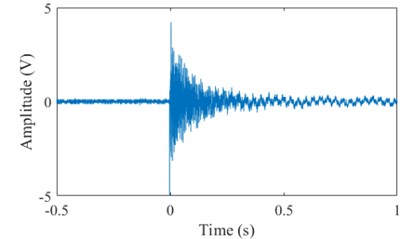
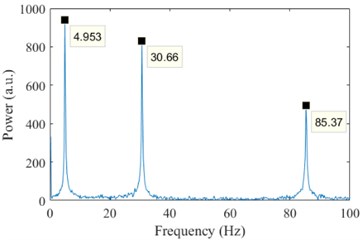
Fig. 3 shows the accelerometer readings and the corresponding FFTs. The FFT reveal the frequencies of the first three modes: 4.95 Hz, 30.66 Hz, and 85.37 Hz. Also, analytic frequencies calculated by using classical structural dynamics concepts [18] to validate accelerometer readings which are 4.90 Hz, 30.7 Hz, and 85.97 Hz. It can be easily seen that experimental data and analytical prediction are in good agreement.
Fig. 3Accelerometer reading and corresponding Fast Fourier Transform
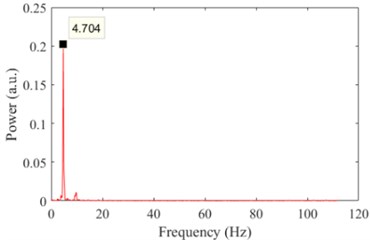
The results of the image processing are presented in Fig. 4. As the frame rate was 240 Hz the graphs extend to 120 Hz, corresponding to the Nyquist frequency of the videos. The graphs show the clear presence of the first mode. The empirical value of 4.70 Hz match very well the values determined by the accelerometer.
Fig. 4Frequency of vibration of the beam as measured with the vision-based algorithm
4. Conclusions
In this article, a study about the use of a smartphone to capture some vibration characteristics of cantilever slender beam was presented. One slender cantilever beam was triggered by using a hammer and recorded with a conventional accelerometer attached to the beam and a smartphone operating at 240 frames per second. The results of the experiments clearly demonstrated that the new non-contact method can be reliably replace conventional accelerometers as the frequency found with both methods matched very well. The results also proved that the combined use of a smartphone and the proposed imaging algorithm can be used as a non-contact monitoring technique. As such, the proposed non-destructive non-contact evaluation method may be considered in the future, after proper research and development, for the field measurement of frequency.
The main advantage of a smartphone is the versatility: a typical user-end camera is a device limited to capture videos but then these videos must be transferred to a computer for further analysis. Future studies shall validate the repeatability of the proposed methodology and improve the image processing algorithm in order to be embeddable in the smartphones for rapid field assessment of critical infrastructures.
References
-
Di Maio D., Ewins D. J. Continuous Scan, a method for performing modal testing using meaningful measurement parameters; Part I. Mechanical Systems and Signal Processing, Vol. 25, Issue 8, 2011, p. 3027-3042.
-
Stanbridge A. B., Ewins D. J. Modal testing using a scanning laser doppler vibrometer. Mechanical Systems and Signal Processing, Vol. 13, Issue 2, 1999, p. 255-270.
-
Chen J. G., Wadhwa N., Cha Y.-J., Durand F., Freeman W. T., Buyukozturk O. Modal identification of simple structures with high-speed video using motion magnification. Journal of Sound and Vibration, Vol. 345, 2015, p. 58-71.
-
Wadhwa N., Freeman W. T., Durand F., Wu H.-Y., Davis A., Rubinstein M., Shih E., Mysore G. J., Chen J. G., Buyukozturk O., Guttag J. V. Eulerian video magnification and analysis. Communications of the ACM, Vol. 60, Issue 1, 2016, p. 87-95.
-
Cha Y.-J., Chen J., Buyukozturk O. Motion magnification based damage detection using high speed video. Proceedings of the 10th International Workshop on Structural Health Monitoring, 2015.
-
Davis A., Rubinstein M., Wadhwa N., Mysore G. J., Durand F., Freeman W. T. The visual microphone: passive recovery of sound from video. ACM Transactions on Graphics, Vol. 33, Issue 4, 2014, p. 1-10.
-
Davis A., Bouman K. L., Chen J. G., Rubinstein M., Buyukozturk O., Durand F., Freeman W. T. Visual vibrometry: estimating material properties from small motions in video. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 39, Issue 4, 2017, p. 732-745.
-
Poozesh P., Sarrafi A., Mao Z., Avitabile P., Niezrecki C. Feasibility of extracting operating shapes using phase-based motion magnification technique and stereo-photogrammetry. Journal of Sound and Vibration, Vol. 407, Issue 27, 2017, p. 350-366.
-
Feng D., Feng M. Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection – a review. Engineering Structures, Vol. 156, 2018, p. 105-117.
-
Molina Viedma A.-J., Felipe Sesé L., López Alba E., Díaz F. High frequency mode shapes characterisation using digital image correlation and phase-based motion magnification. Mechanical Systems and Signal Processing, Vol. 102, 2018, p. 245-261.
-
Wadhwa N., Rubinstein M., Durand F., Freeman W. T. Phase-based video motion processing. ACM Transactions on Graphics, Vol. 32, Issue 4, 2013, p. 1-10.
-
Chen J. G., Wadhwa N., Durand F., Freeman W. T., Buyukozturk O. Developments with motion magnification for structural modal identification through camera video. Dynamics of Civil Structures, Conference Proceedings of the Society for Experimental Mechanics Series, Springer, Vol. 2, 2015, p. 49-57.
-
Yang Y., Dorn C., Mancini T., Talken Z., Kenyon G., Farrar C., Mascareñas D. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification. Mechanical Systems and Signal Processing, Vol. 85, 2017, p. 567-590.
-
Fleet D. J., Jepson A. D. Computation of component image velocity from local phase information. International Journal of Computer Vision, Vol. 5, Issue 1, 1990, p. 77-104.
-
Yang Y., Dorn C., Farrar C., Mascarenas D. Full-field imaging and modeling of structural dynamics with digital video cameras. Proceedings of the 11th International Workshop on Structural Health Monitoring, 2017.
-
Ferrer B., Espinosa J., Roig A. B., Perez J., Mas D. Vibration frequency measurement using a local multithreshold technique. Optics Express, Vol. 21, Issue 22, 2013, p. 26198-208.
-
The MathWorks, MATLAB, R2017a.
-
Tedesco J. W., Mcdougal W. G., Ross C. A. Structural Dynamics: Theory and Applications. Addison Wesley Longman, 1999.
About this article
The first author was supported by the Scientific and Technological Research Council of Turkey (TUBITAK) 2214/A International Doctoral Research Fellowship Programme (Grant No. #1059B141600085). The experiments were held at the Laboratory for Nondestructive Evaluation and Structural Health Monitoring Studies at University of Pittsburgh. Authors would also like to acknowledge Piervincenzo Rizzo and Amir Nasrollahi from the Department of Civil and Environmental Engineering at University of Pittsburgh and also, David Mas and Belen Ferrer from the Department of Civil Engineering at University of Alicante.
