Abstract
The goal of this paper is to inspect the influence of non-linear inertia on dynamic response of multi-story asymmetric buildings. In this study unlike conventional linear approach, the non-linear inertial terms are considered in the equations of motion. For considering non-linear inertia, the motion equations are derived in local rotary coordinates system. Also, the stiffness and damping parameters are defined in the rotary coordinates system. In the novel approach which is proposed in this paper, the motion equations are different with conventional linear approach. Numerical examples are presented to compare the response of the proposed model and conventional linear model. The modeled building response is derived under harmonic excitation. The results show that if non-linear inertia is considered, the dynamic response of asymmetric multi-story buildings may become different with conventional linear approach.
1. Introduction
Torsional motions in asymmetric buildings and can cause severe damages [1]. So, it is important to carefully investigate the behavior of asymmetric buildings under dynamic loads. Many researchers have studied the effects of non-linear inertia on behavior of mechanical systems. Mayet and Ulbrich studied the non-linear detuning of centrifugal pendulum vibration absorber [2]. Mamandi et al. studied the non-linear behavior of an inclined beam subjected to a moving load [3]. In the field of structural engineering little attention has been paid to non-linear inertia and a few number of researchers have studied the effect of non-linear inertia on dynamic response of structural systems. Amin Afshar and Aghaei Pour studied the inertia non-linearity in irregular-plan isolated structures under seismic excitations [4]. Amini and Amin Afshar studied the effect of non-linear inertia on dynamic response of single story asymmetric building [5].
The effect of non-linear inertia in dynamic response of multi-story asymmetric buildings has not been studied enough. In this study non-linear inertia is considered in equations of motion and for considering non-linear inertia the equations of motion in each story is defined in local rotary coordinates system.
2. Non-linear differential equations of motion
As seen in Fig. 1(a), a single story building is subjected to ground excitation in excitation in and directions. The floor mass center is denoted by C.M. and C.R. represents the center of stiffness of the story. Based on Amini and Amin Afshar approach, the non-linear equations of motion in local rotary coordinates system can be expressed as (see Fig. 1(b)) [5]:
In Eqs. (1)-(3), is the distance between C.M. and C.R. It is assumed that C.R. is located on axis. The value of can be calculated by:
where represents the stiffness of the th element resisting in direction. In Eqs. (1)-(3), denotes the total mass of the floor and is the floor radius of gyration about the mass center, and are the ground accelerations in and directions, and are displacements of the floor mass center in the and directions and is the rotation of the floor about the axis. Also, and are total stiffness of the story in the and directions. The parameter is the torsional stiffness of the story about C.R. and can be calculated by:
where represents the stiffness of the th resisting element in direction. Moreover , and are damping coefficients [5].
Fig. 1a) The plan of asymmetric building, b) global (XYZ) and local (xyz) coordinates systems; – structure elements [4]
![a) The plan of asymmetric building, b) global (XYZ) and local (xyz) coordinates systems; – structure elements [4]](https://static-01.extrica.com/articles/19856/19856-img1.jpg)
a)
![a) The plan of asymmetric building, b) global (XYZ) and local (xyz) coordinates systems; – structure elements [4]](https://static-01.extrica.com/articles/19856/19856-img2.jpg)
b)
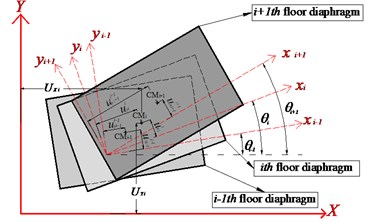
The motion equations of the multi-story building will be derived according to Eqs. (1)-(3). The equations of motion of the th story will be derived in the local rotary system of coordinates. As seen in Fig. 2 the coordinates system is located on the base of the building and rotates by an angle . It should be noted that in the conventional linear approach the motion equations are derived in fixed system of coordinates. The motion equations of the th story can be expressed as [6]:
where denotes the inertial forces, which is exerted to the th floor. Also the term is the force of resisting elements in th story which is applied to the th floor and the term is the force of resisting elements in th story which is exerted to the th floor. Also, the terms and denote the damping forces. In Eq. (6), denotes the mass matrix of the th floor. The matrix can be expressed as:
where is the mass of the th floor and is the th floor radius of gyration about the mass center. In Eq. (6), represents the total acceleration of the th floor center of mass in the local coordinates system. The vector can be calculated by [6]:
where and are displacements of the th floor mass center in and directions (see Fig. 2), and are the ground translational accelerations. Moreover in Eq. (6), is the stiffness matrix of the th story. The matrix is defined in the directions of coordinates system. The matrix can be expressed as:
where and are the th story stiffness in the and directions. The parameters and are defined in the rotary coordinates system. The parameter is the torsional stiffness of the th story about the th story center of stiffness. Also, is the distance between the mass center and the center of the stiffness of the th story. In Eq. (6), is the damping matrix of the th story. The matrix can be expressed as:
where , and are the th story damping coefficients. These coefficients are defined in coordinates system. If and represent the displacements of the th floor center of mass in the and direction (see Fig. 2), the relationship between and vectors can be expressed as:
where is the rotation matrix about the axis by an angle . Also, the vector is defined by:
Moreover in Eq. (6), and are defined by:
where the vector denotes the th floor displacement. Also is the th floor displacement vector. The vectors and , are defined in the rotary coordinates system. The relationship between and can be expressed as:
where is defined by .
Now in Eq. (6), the matrix will be derived. The vector is defined by:
As it was mentioned before, the vector denotes the force of the resisting elements in th story which is applied to the th floor. Vector is defined in coordinates system. It is obvious that the reaction of the vector is applied to the th floor. To define the vector in system of coordinates, it can be rotated about axis by an angle . So, following equation can be written:
where vector is the th story resisting elements force which is applied to the th floor. Vector is defined in coordinates system. As it was mentioned earlier, in Eq. (6) vector is defined by:
According to Eqs. (17)-(19) the term can be expressed as:
and so can be expressed as:
Also, similar method can be used to derive and it can be expressed as:
where is the th floor damping matrix which is defined in coordinates system.
Fig. 2Local rotary xiyizi coordinates system; CMi denotes the ith floor center of mass
3. Numerical studies
Here, for comparing the response of proposed model and conventional linear model a five story building model is considered. The modeled building properties are listed in Table 1. It should be noted that the modeled structures is a scaled buildings. The damping ratio of the modeled building is selected to be 0.5 %. Moreover, the natural frequencies of the first three modes are listed in Table 2. The ground harmonic excitation in and directions is selected to be:
where the parameter denoted the amplitude of the excitation and is the excitation arrival angle with respect to direction.
Table 1Modeled building properties
Story No. | Mass (N/(cm/s2)) | and (N/cm) | (N.cm) | (cm) | (cm) |
1 | 0.1 | 142.1 | 32095 | 9.67 | 20 |
2 | 0.1 | 142.1 | 32095 | 9.67 | 20 |
3 | 0.1 | 142.1 | 32095 | 9.67 | 20 |
4 | 0.1 | 142.1 | 32095 | 9.67 | 20 |
5 | 0.1 | 142.1 | 32095 | 9.67 | 20 |
Table 2Modeled building natural frequencies in first thee modes
(rad/s) | (rad/s) | (rad/s) |
5.39 | 10.73 | 12.29 |
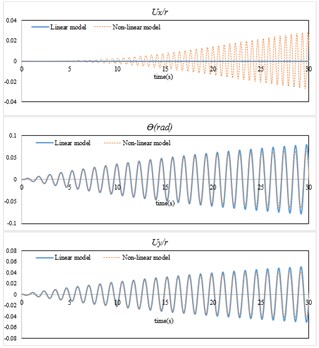
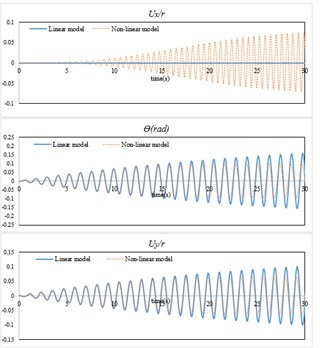
The response of top floor mass center is shown in Fig. 3. It is seen that the response of linear and non-linear models is quite different. The response of top floor mass center in linear model and direction is zero. But in non-linear model the top story mass center oscillates in direction. In non-linear model, after initial steps of excitation the amplitude of the response in direction increases. Moreover, in non-linear model the amplitude of the response in direction reaches a constant value after initial oscillations. It is seen that when the amplitude of excitation is increased, the difference between linear and non-linear model responses become more.
Fig. 3Top story response of the modeled building: a) A= 0.005, β= 90° and ω=ω1, b) A= 0.01, β= 90° and ω=ω1
a)
b)
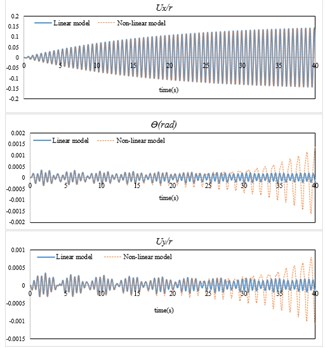
In Fig. 4 the response of the top floor mass center is shown. In this figure the parameter is selected to be near to zero. In Fig. 4(a), the response of the both linear and non-linear models are identical in direction and the difference between these two models can be ignored. In the response of direction and , linear and non-linear models have the same response in initial steps of excitation. But after initial steps of oscillation the response of direction and increases.
As seen in Fig. 4 when the excitation amplitude is increased, the difference between linear and non-linear models becomes more. In Fig. 4(b) when the amplitude of the response in direction reaches a certain value; the amplitude suddenly decreases in direction and again increases. Moreover, after initial steps of excitation the response of direction increases. When the energy amount in the dominant mode of direction reaches a certain value, this mode is saturated, and the energy is transferred to other modes.
Fig. 4Top story response of the modeled building: a) A= 0.01, β= 0.05 rad and ω=ω2, b) A= 0.03, β= 0.05 rad and ω=ω2
a)
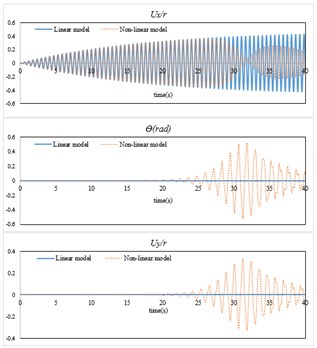
b)
4. Conclusions
In this study unlike conventional linear approach, the non-linear inertia was considered in equations of motion of multi-story asymmetric building. For considering non-linear inertia, the equations of motion were derived in local rotary coordinates system. It was seen that the conventional linear approach is weak to model the behavior of asymmetric buildings and considering non-linear inertia leads to different response. In the modeled structure if the amplitude of the excitation is increased the difference between linear and proposed non-linear models become more. Also, in some cases energy transfer between the modes is observed.
References
-
Amin Afshar M., Amini F. Non-linear dynamics of asymmetric structures under 2:2:1 resonance. International Journal of Non-Linear Mechanics, Vol. 47, 2012, p. 823-835.
-
Mayet J., Ulbrich H. First-order optimal linear and nonlinear detuning of centrifugal pendulum vibration absorbers. Journal of Sound and Vibration, Vol. 335, 2015, p. 34-54.
-
Mamandi A., Kargarnovin M. H., Younesian D. Nonlinear dynamics of an inclined beam subjected to a moving load. Nonlinear Dynamics, Vol. 60, 2010, p. 277-293.
-
Amin Afshar M., Aghaei Pour S. On inertia nonlinearity in irregular-plan isolated structures under seismic excitations. Journal of Sound and Vibration, Vol. 363, 2016, p. 495-516.
-
Amini F., Amin Afshar M. Saturation in asymmetric structures under internal resonance. Acta Mechanica, Vol. 221, 2011, p. 353-368.
-
Amini F., Rezazadeh H., Amin Afshar M. Adaptive control of rotationally non-linear asymmetric structures under seismic loads. Structural Engineering and Mechanics, Vol. 65, Issue 6, 2018, p. 721-730.
