Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox

Chen, Yuan; Zhu, Ru Peng; Feng, Zai Chun; Jin, Guang Hu; Zhang, Wei

doi:10.21595/vp.2018.19707

Vibroengineering Procedia

Browse Procedia

Published: 20 April 2018

Check for updates

Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox

Yuan Chen¹

Ru Peng Zhu²

Zai Chun Feng³

Guang Hu Jin⁴

Wei Zhang⁵

^{1, 2, 4, 5}College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

³Department of Mechanical and Aerospace Engineering, University of Missouri, Columbia, USA

Corresponding Author:

Ru Peng Zhu

Cite the article Download PDF

Downloads 1523

CrossRef Citations 2

Abstract

The elastohydrodynamic lubrication (EHL) contact model is established, the oil film stiffness is calculated based on Dowson-Higginson empirical minimum thickness equation. The vibration model of single-rotor three-input helicopter main reducer is proposed by lumped mass method, and nonlinear factors like oil film stiffness, dynamic meshing force are taken into account. The influence of oil film stiffness on system natural frequency is analyzed as well. The results show that oil film stiffness of the internal and external meshing pairs in the planetary gear system have greater impact on the natural frequency, which tends to destabilize the system. Therefore, the planetary gear train is the most crucial branch regarding the system splash lubrication. When all the oil film stiffness in the system are greater than 4×10⁹ N/m, the natural frequencies tend to be stable. This study can provide the theoretical reference for the lubrication characteristics in the single-rotor multi-input helicopter.

1. Introduction

To protect the tooth surface, the gears normally work in the lubrication condition. With load and entrainment velocity, the lubricating oil forms a certain film thickness on the contact surface of the gear pair. When working condition changes, the film follows with deformation, the oil film stiffness changes. Study of the influence law of the oil film stiffness on the natural characteristics has important engineering significance.

Within the scope of the multi-stage helicopter main reducer, especially regarding natural frequency analysis. Kahraman [1] applied eigenvalue solution and the modal summation technique to predict the free and forced vibrations of the multi-stage gear transmission system. Huang [2] established a finite element model of a parallel three-shaft gear-rotor coupling system and analyzed the influences of the mesh stiffness, the installation angle, the helix angle and the bearing stiffness on the natural characteristics. Choy [3] analyzed the modal characteristics by using the matrix-transfer technique. Chen [4] studied the influence of torsional stiffness on natural characteristics of four-stage main transmission system in three-engine helicopter. Li [5] investigated the damping mechanism and EHL characteristics at the interface of the two DOF spur gear pair.

In summary, at present, the influence of oil film stiffness on the multi-stage system natural characteristics, is not to be investigated, according to the limited published issues. Therefore, it is of great theoretical significance and engineering value to study the mechanism of oil film stiffness on vibration and noise in gear transmission.

2. System dynamic model

2.1. Dynamic modeling

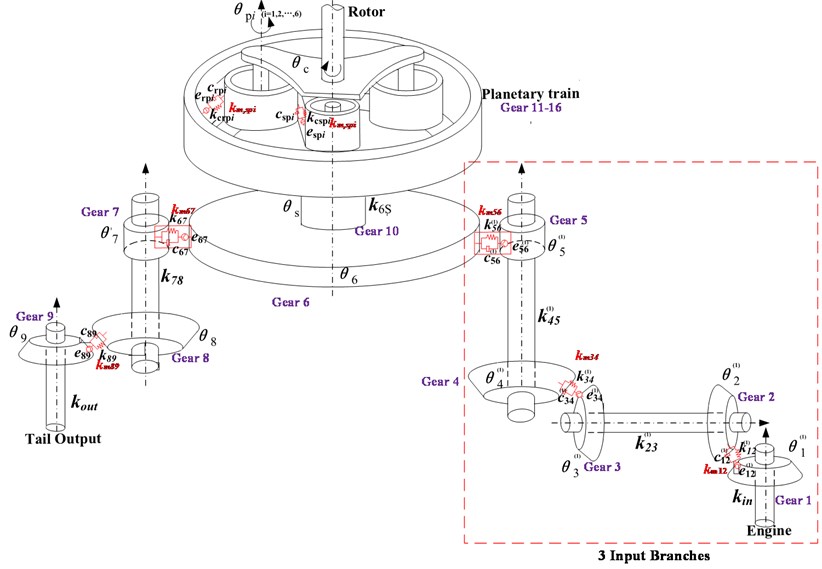
The dynamic model of single-rotor three-input helicopter main reducer is shown in Fig. 1 [6]. The system includes three input branches, a tail output branch and a planet train branch. $θ_{1}^{(j)}$ , $θ_{2}^{(j)}$ , $θ_{3}^{(j)}$ , $θ_{4}^{(j)}$ , $θ_{5}^{(j)}$ , $θ_{6}$ , $θ_{c}$ , $θ_{7}$ , $θ_{8}$ , $θ_{9}$ , $θ_{s}$ and $θ_{p i}$ are rotational DOF of gear system in each stage. $k_{i n}$ , $k_{23}$ , $k_{45}$ , $k_{78}$ , $k_{o u t}$ and $k_{6 s}$ are torsional stiffness of shafts connecting each gear pair; $c_{12}$ , $c_{34}$ , $c_{56}$ , $c_{s p i}$ and $c_{r p i}$ are meshing damping of each gear pair; $k_{12}$ , $k_{34}$ , $k_{56}$ , $k_{s p i}$ and $k_{r p i}$ are meshing stiffness of each gear pair; $k_{m}$ represents oil film stiffness.

Fig. 1Dynamic model of single-rotor three-input helicopter main reducer

2.2. Differential equation

For the EHL model, Dowson achieved a large amount of data through numerical simulation and experimental measurements and proposed the empirical equation for calculating the minimum oil film thickness. The Dowson-Higginson minimum oil film thickness empirical equation is [7]:

1

h_{m} = 2.65 U^{0.7} G^{0.54} W^{- 0.13} R,

where $U$ , $G$ , $W$ are dimensionless speed, material, load respectively:

U = \frac{η_{0} u_{r}}{E^{'} R}, G = α_{l} E^{'}, W = \frac{F}{E^{'} R}, \frac{2}{E^{'}} = \frac{1 - v_{1}^{2}}{E_{1}} + \frac{1 - v_{2}^{2}}{E_{2}},

where, $F$ is the load in meshing line, $E'$ is the equivalent elastic modulus, $R$ is synthetical curvature radius, $u_{r}$ is entrainment velocity, $α_{l}$ is pressure-viscosity coefficient, $η_{0}$ is dynamic viscosity. $E_{1}$ , $E_{2}$ and $v_{1}$ , $v_{2}$ are the contact elastic modulus and Poisson’s ratio.

The minimum oil film stiffness based on Dowson-Higginson oil film thickness can be derived by taking the derivative of Eq. (1):

2

k_{h m} = 7.69 B E^{'} {R (2.65 U}^{0.7} G^{0.54} R)^{7.69} h_{m}^{- 8.69},

here, $B$ is contact length.

Time-varying meshing stiffness can be expanded in the Fourier series with the fundamental meshing frequency:

3

\{\begin{matrix} k_{12}^{(j)} (t) = k_{m 12} + k_{a 12} \sin (ω_{12} t + β_{12}), \\ k_{34}^{(j)} (t) = k_{m 34} + k_{a 34} \sin (ω_{34} t + β_{34}), \\ k_{56}^{(j)} (t) = k_{m 56} + k_{a 56} \sin (ω_{56} t + β_{56}), \\ k_{67} (t) = k_{m 67} + k_{a 67} \sin (ω_{67} t + β_{67}), \\ k_{89} (t) = k_{m 89} + k_{a 89} \sin (ω_{89} t + β_{89}), \\ k_{s p i} (t) = k_{m, s p i} + k_{a, s p i} \sin (ω t + β_{s p i}), \\ k_{r p i} (t) = k_{m, r p i} + k_{a, r p i} \sin (ω t + β_{r p i}), \end{matrix}

where $k_{12}^{(j)} (t)$ , $k_{34}^{(j)} (t)$ , $k_{56}^{(j)} (t)$ , $k_{67} (t)$ , $k_{89} (t)$ , $k_{s p i} (t)$ and $k_{r p i} (t)$ are time-varying mesh stiffness in each gear pair. $k_{m}$ is average meshing stiffness considering oil film stiffness, $k_{a}$ is maximum variable meshing stiffness. $β$ is initial meshing phase.

The differential equation of the single-rotor multi-input helicopter main reducer can be deduced through Newton’s law, as shown in Eq. (4):

4

\{\begin{array}{l} J_{1} {\ddot{θ}}_{1}^{(j)} + [F_{12}^{p (j)} (t) + F_{12}^{d (j)} (t)] r_{1} + k_{i n} θ_{1}^{(j)} = T_{E j}, \\ J_{2} {\ddot{θ}}_{2}^{(j)} - [F_{12}^{p (j)} (t) + F_{12}^{d (j)} (t)] r_{2} + k_{23}^{(j)} (θ_{2}^{(j)} - θ_{3}^{(j)}) = 0, \\ J_{3} {\ddot{θ}}_{3}^{(j)} + [F_{34}^{p (j)} (t) + F_{34}^{d (j)} (t)] r_{3} + k_{23}^{(j)} (θ_{3}^{(j)} - θ_{2}^{(j)}) = 0, \\ J_{4} {\ddot{θ}}_{4}^{(j)} - [F_{34}^{p (j)} (t) + F_{34}^{d (j)} (t)] r_{4} + k_{45}^{(j)} (θ_{4}^{(j)} - θ_{5}^{(j)}) = 0, \\ J_{5} {\ddot{θ}}_{5}^{(j)} + [F_{56}^{p (j)} (t) + F_{56}^{d (j)} (t)] r_{5} + k_{45}^{(j)} (θ_{5}^{(j)} - θ_{4}^{(j)}) = 0, \\ J_{6} {\ddot{θ}}_{6} - \sum_{j = 1}^{3} [F_{56}^{p (j)} (t) + F_{56}^{d (j)} (t)] r_{6} + [F_{67}^{p (j)} (t) + F_{67}^{d (j)} (t)] r_{6} + k_{6 s} (θ_{6} - θ_{s}) = 0, \\ J_{7} {\ddot{θ}}_{7} - [F_{67}^{p (j)} (t) + F_{67}^{d (j)} (t)] r_{7} + k_{78} (θ_{7} - θ_{8}) = 0, \\ J_{8} {\ddot{θ}}_{8} + [F_{89}^{p (j)} (t) + F_{89}^{d (j)} (t)] r_{8} + k_{78} (θ_{8} - θ_{7}) = 0, \\ J_{9} {\ddot{θ}}_{9} - [F_{89}^{p (j)} (t) + F_{89}^{d (j)} (t)] r_{9} + k_{R R} θ_{9} = - T_{R R}, \\ J_{s} {\ddot{θ}}_{s} + \sum_{i = 1}^{N} [F_{s p i}^{p} (t) + F_{s p i}^{d} (t)] r_{s} - k_{6 s} (θ_{6} - θ_{s}) = 0, \\ J_{p} {\ddot{θ}}_{p i} - [F_{s p i}^{p} (t) + F_{s p i}^{d} (t)] r_{p} + [F_{r p i}^{p} (t) + F_{r p i}^{d} (t)] r_{p} = 0, \\ [J_{c} + \sum_{i = 1}^{N} (m_{p i} r_{c}^{2})] {\ddot{θ}}_{c} - \sum_{i = 1}^{N} [F_{s p i}^{p} (t) + F_{s p i}^{d} (t) + F_{r p i}^{p} (t) + F_{r p i}^{d} (t)] r_{c} \cos α = - T_{M R}, \end{array}

where $T_{E j}$ is the torque of engine $j$ ( $j =$ 1, 2, 3); $T_{R R}$ and $T_{M R}$ are the torque of tail branch and planet carrier. $F^{p}$ and $F^{d}$ are dynamic meshing and damping forces. $J_{c}$ is carrier moment of inertia.

In addition, after the decomposition and recombination of Eq. (4), it can be expressed with mass matrix, damping matrix and stiffness matrix form. By setting the value of damping item and external excitation item to be zero, the vibration differential equation of the system under free condition can be obtained.

3. System natural characteristics analysis

Gear parameters are listed in Table 1, and EHL parameters are shown in Table 2.

Table 1Gear parameters

Gear	Tooth number	Module	Face width (mm)
Gear 1	30	4.5	40
Gear 2	85	4.5	40
Gear 3	40	5	45
Gear 4	90	5	45
Gear 5	25	4.75	40
Gear 6	142	4.75	40
Gear 7	40	5	40
Gear 8	60	5	35
Gear 9	70	5	35
Gear 10	68	5	28
Gear 11-16	37	5	28

Table 2EHL parameters

Parameter	Value
Dynamic viscosity $η_{0}$ (Pa·s)	0.04
Pressure-viscosity coefficient $α_{l}$ (Pa^-1)	2.2×10^-8
Elastic modulus $E_{1}$ (Pa)	2×10¹¹
Elastic modulus $E_{2}$ (Pa)	2×10¹¹
Poisson’s ratio $v_{1}$	0.3
Poisson’s ratio $v_{2}$	0.3

In order to explore the influence law of oil film stiffness on natural characteristics of the system, the natural frequencies of the first five orders are calculated and depicted in Fig. 2. Fig. 2(a) and Fig. 2(b) are the influence of oil film stiffness on natural frequency in first stage and the second stage, as shown in the figure, when the oil film stiffness is greater than 2×10⁹N/m, the natural frequencies no longer change. When the oil film stiffness is less than 2×10⁹N/m, the decrease of natural frequency of the fourth and fifth order is the most obvious. Fig. 2(c) shows the effect of oil film stiffness on the natural frequency in the third stage. The figure shows that when $k_{56}$ is less than 2×10⁹N/m, the first-order natural frequency decreases rapidly. Fig. 2(d) and Fig. 2(e) show the impact of oil film stiffness on natural frequency in the tail branch. When $k_{67}$ is less than 4×10⁹N/m, the first-order natural frequency decreases sharply; when $k_{89}$ is less than 0.5×10⁹N/m, the natural frequency of the fifth order decreases while the natural frequencies of other orders do not change. Fig. 2(f) and Fig. 2(g) are the influence law of planetary gear train on the system natural frequency, as seen from the figure, when the internal and external meshing oil film stiffness are equal to 0.7×10⁹N/m and 0.9×10⁹N/m, the natural frequency of each order has a sudden drop-point, which could easily destabilize the system. Therefore, the planetary gear train is the most important branch in splash lubrication analysis, the oil film stiffness cannot be too small in mechanical design.

4. Conclusions

In this paper, a dynamic model of single-rotor three-input helicopter main reducer is proposed and influence laws of the oil film stiffness are calculated, the analysis results enable us to draw the following conclusions:

1) The influence laws of the oil film stiffness of the two gear pairs in the input branch are almost the same, the influence laws of the internal and external meshing pairs in the planetary gear system are also very similar, therefore these two branches should consider all components within the branch.

Fig. 2Impact of oil film stiffness on first five orders natural frequency

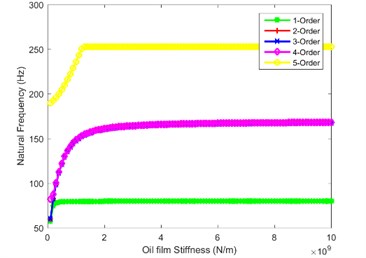
a) $k_{12}$

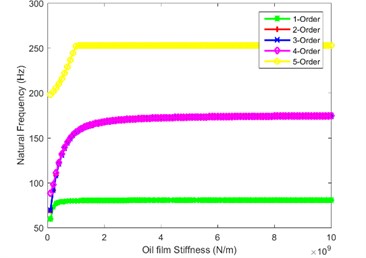
b) $k_{34}$

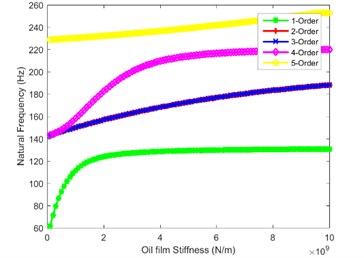
c) $k_{56}$

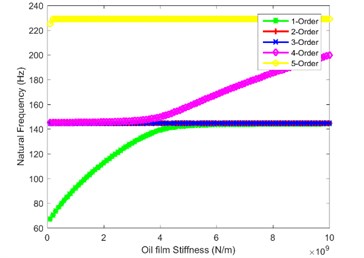
d) $k_{67}$

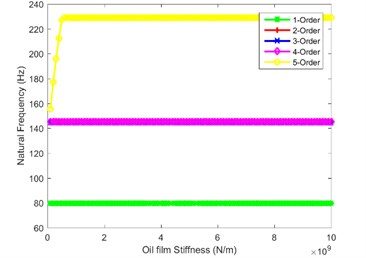
e) $k_{89}$

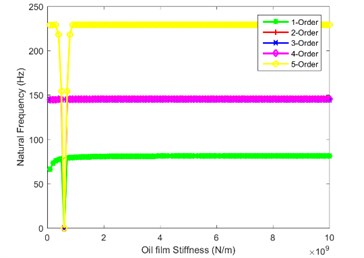
f) $k_{m s p}$

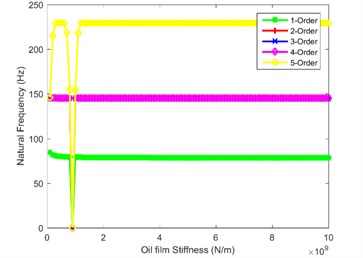
g) $k_{m r p}$

2) When the oil film stiffness is small, the natural frequencies of each order can be variable. When the oil films stiffness of all meshing pairs in the system is more than 4×10⁹ N/m, the natural frequencies tend to be stable.

3) Planetary gear train is the most critical branch of the single-rotor three-input system regarding splash lubrication, so their oil film stiffness cannot be too small during working condition.

References

Kahraman A., Zini D. M., Kienzle K. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: model and experiment. ASME Journal of Vibrations and Acoustics, Vol. 126, Issue 3, 2004, p. 398-406.

Publisher
Huang J., Zhang S., Zhang Y. The influences of system parameters on the natural characteristics of a parallel multi-shaft gear-rotor system. Machinery Design and Manufacture, Vol. 7, 2013, p. 15-17, (in Chinese).

Search CrossRef
Choy F. K., Ruan Y. F., R. K., Zakrajsek J. J., Townsend D. P. Modal analysis of multistage gear systems coupled with gearbox vibrations. Journal of Mechanical Design, Vol. 114, Issue 3, 2008, p. 486-497.

Publisher
Chen Y., Zhu, R. P., Xiong, Jin, G. H. Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter. Vibroengineering Procedia, Vol. 12, 2017, p. 19‑23.

Publisher
Li S., Kahraman A. A spur gear mesh interface damping model based on elastohydrodynamic contact behaviour. International Journal of Powertrains, Vol. 1, Issue 1, 2011, p. 4-21.

Publisher
Bianchi A., Rossi S. Modeling and finite element analysis of a complex helicopter transmission including housing, shafts and gears. 1997, http://hdl.handle.net/20.500.11881/3273.

Publisher
Ye Y. D., Zhou Z. B. Research on influence of gear parameters on lubrication oil film thickness under condition of elasto hydrodynamic lubrication. Journal of Machine Design, Vol. 29, 9, p. 73-76, (in Chinese).

Search CrossRef

Cited by

Designing of Drive Systems in the Aspect of the Desired Spectrum of Operation

(2021)

A New Mathematical Modeling Method for Four-Stage Helicopter Main Gearbox and Dynamic Response Optimization

(2019)

About this article

Received

29 January 2018

Accepted

05 February 2018

Published

20 April 2018

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2018.19707

Keywords

helicopter main reducer

natural characteristics

oil film stiffness

nonlinear dynamics

Acknowledgements

This work is supported by the National Natural Science Foundation of PRC (Grant No. 51775265 and 51475226); China Scholarship Council; China Association for Science and Technology.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 06 11

Design, analysis and fabrication of a fully articulated helicopter main rotor system

Arafat Ahmed Shamol, Samin Yaser Ahmed, Md. Ariful Islam Shubho, Towsibur Rahman

Research article

2020 04 02

Nonlinear dynamic characteristics of face gear pair for helicopter

Wang Li, Ning Zhao

Research article

2019 02 15

Research on static load sharing characteristics of power split two-stage five-branching star gearing drive system

Hao Dong, Zhi-yu Liu, Xiao-long Zhao, Ya-hui Hu

Research article

2018 08 15

Tooth surface friction and its influence on dynamic transmission error of double power input transmission system

G. H. Jin, H. Y. Yang, R. P. Zhu

Y. Chen, R. P. Zhu, Z. C. Feng, G. H. Jin, and W. Zhang, “Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox,” Vibroengineering PROCEDIA, Vol. 17, pp. 7–12, Apr. 2018, https://doi.org/10.21595/vp.2018.19707

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.19707
UR  - https://doi.org/10.21595/vp.2018.19707
TI  - Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox
T2  - Vibroengineering PROCEDIA
AU  - Zhu, Ru Peng
AU  - Chen, Yuan
AU  - Feng, Zai Chun
AU  - Jin, Guang Hu
AU  - Zhang, Wei
PY  - 2018
DA  - 2018/04/20
PB  - JVE International Ltd.
SP  - 7-12
VL  - 17
SN  - 2345-0533
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhu_2018,
	doi = {10.21595/vp.2018.19707},
	url = {https://doi.org/10.21595/vp.2018.19707},
	year = 2018,
	month = {apr},
	publisher = {{JVE} International Ltd.},
	volume = {17},
	pages = {7--12},
	author = {Ru Peng Zhu and Yuan Chen and Zai Chun Feng and Guang Hu Jin and Wei Zhang},
	title = {Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]R. P. Zhu, Y. Chen, Z. C. Feng, G. H. Jin, and W. Zhang, “Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox,” Vibroengineering PROCEDIA, vol. 17, pp. 7–12, Apr. 2018, doi: 10.21595/vp.2018.19707.

Copy IEEE

Copied to clipboard!

Zhu, Ru Peng, Yuan Chen, Zai Chun Feng, Guang Hu Jin, and Wei Zhang. “Influence of Oil Film Stiffness on Natural Characteristics of Single-Rotor Three-Input Helicopter Main Gearbox.” Vibroengineering PROCEDIA 17 (April 20, 2018): 7–12. https://doi.org/10.21595/vp.2018.19707.

Copy Chicago

Copied to clipboard!

Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox

Abstract

1. Introduction

2. System dynamic model

2.1. Dynamic modeling

2.2. Differential equation

3. System natural characteristics analysis

4. Conclusions

References

Cited by

About this article

Related Articles