Improved numerical approximation of dry friction phenomena

Keywords: dry friction, piecewise linear approximation, vibrations, numerical results, graphical relationships.

1. Introduction

In the numerical investigation of vibration problems with dry friction it is accepted to use some type of approximation to this phenomenon. Often linear variation of the force of friction in a region around zero velocity is assumed. In this paper trigonometric variation is proposed and comparison of numerical results is performed. From the presented results higher precision of this approximation is observed.

Analysis of linear variation of the force of friction in a region around zero velocity is presented in [1]. The role of dry friction is highlighted in [2-4]. Engineering assumptions in modelling systems with dry friction are presented in [5]. Models comprising dry friction are discussed in [6, 7]. Mechanical systems with dry friction are investigated in [8]. Mechanisms for surface cleaning based on dry friction are discussed in [9-12]. Problems of dry friction in the micro scale are investigated in [13-16]. Applications of dry friction in vibration engineering are discussed in [17, 18].

2. Investigation of numerical approximations to dry friction phenomenon

The investigated vibrating system is described by the following equation:

(1)

$m\ddot{u}+c\dot{u}+H+ku=P\mathrm{s}\mathrm{i}\mathrm{n}\omega t,$

where $m$ is the mass of the structure, $c$ is the coefficient of viscous friction, $k$ is the stiffness of the structure, $u$ is the displacement, $P$ is the amplitude of the exciting force, $\omega$ is the frequency of excitation, $H$ is the approximation of the force of dry friction and the upper dot denotes differentiation with respect to time $t$.

In the numerical calculations it is assumed that:

(2)

$H=H_p+C\left(\dot{u}-{\dot{u}}_p\right),$

where $C$ is a function defined further and the subscript $p$ denotes the previous value of the corresponding variable.

Thus, the following equation is solved:

(3)

$m\ddot{u}+\left(c+C\right)\dot{u}+ku=P\mathrm{s}\mathrm{i}\mathrm{n}\omega t-H_p+C{\dot{u}}_p.$

2.1. Conventional linear approximation of dry friction

It is assumed that:

(4)

$C=\left\{\begin{array}{l}\frac{h}{\mathrm{\Delta }},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|<\mathrm{\Delta },\\ 0,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|\ge \mathrm{\Delta },\end{array}\right.$

where $h$ is the coefficient of dry friction and $\mathrm{\Delta }$ determines the width of the transition region.

The following parameters of the investigated structure are assumed: $\omega =$ 1, $h=$ 1.6, $\mathrm{\Delta }=$ 0.8, $c=$ 0.1, $P=$ 4, $m=$ 1, $k=$ 1$.$ Calculations from zero initial conditions are performed and two periods of steady state motions are represented in Fig. 1.

Fig. 1. Steady state motion for linear approximation of dry friction

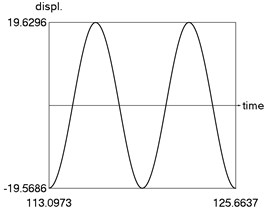
a) Displacement as function of time

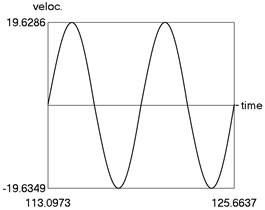
b) Velocity as function of time

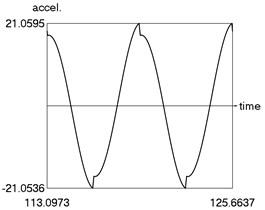
c) Acceleration as function of time

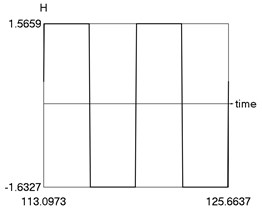
d)$H$ as function of time

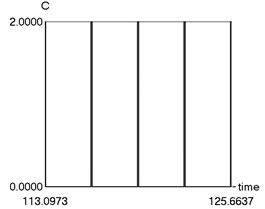
e)$C$ as function of time

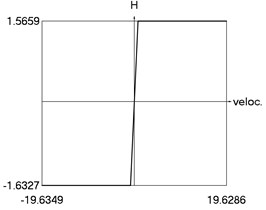
f)$H$ as function of velocity

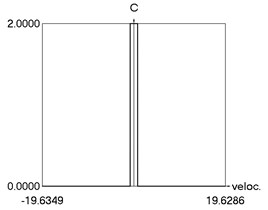
g)$C$ as function of velocity

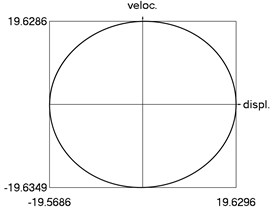
h) Phase trajectory: velocity as function of displacement

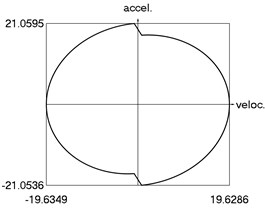
i) Phase trajectory: acceleration as function of velocity

2.2. Trigonometric approximation of dry friction

It is assumed that:

(5)

$C=\left\{\begin{array}{l}\frac{d}{d\dot{u}}\left(h\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi }{2}\frac{\dot{u}}{\mathrm{\Delta }}\right)=h\frac{\pi }{2}\frac{1}{\mathrm{\Delta }}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi }{2}\frac{\dot{u}}{\mathrm{\Delta }},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|<\mathrm{\Delta },\\ 0,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|\ge \mathrm{\Delta }.\end{array}\right.$

Calculations from zero initial conditions are performed and two periods of steady state motions are represented in Fig. 2.

From the obtained results higher precision of trigonometric approximation is seen. This is especially evident from the indicated minimum and maximum values of $H$.

Fig. 2. Steady state motion for trigonometric approximation of dry friction

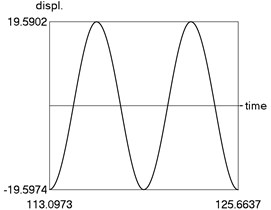
a) Displacement as function of time

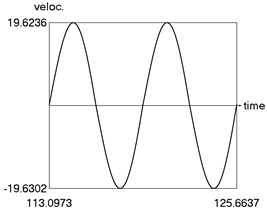
b) Velocity as function of time

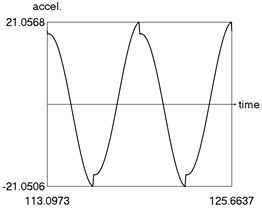
c) Acceleration as function of time

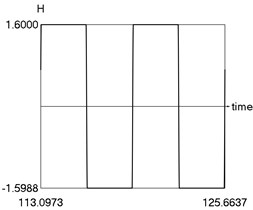
d)$H$ as function of time

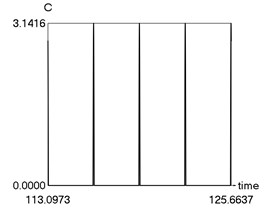
e)$C$ as function of time

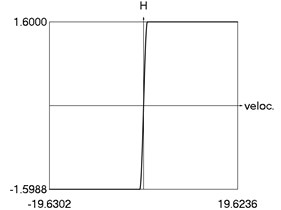
f)$H$ as function of velocity

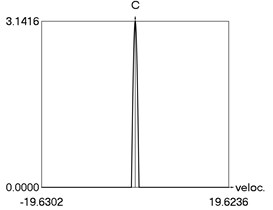
g)$C$ as function of velocity

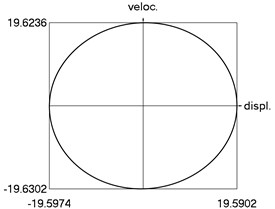
h) Phase trajectory: velocity as function of displacement

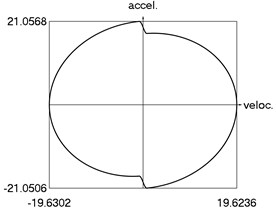
i) Phase trajectory: acceleration as function of velocity

3. Investigation of more complicated numerical approximation to dry friction phenomenon

The increase of the coefficient of dry friction near to the value of zero velocity is often assumed. It is considered that:

(6)

$\frac{h}{\mathrm{\Delta }}=\frac{h_a}{{\mathrm{\Delta }}_a},$

where $h_a$ is the increase of the coefficient of dry friction near to the value of zero velocity and ${\mathrm{\Delta }}_a$ determines the width of the transition region between the values of the coefficient of dry friction $h$ and $h+h_a$.

From this equation the relationship between $h_a$ and ${\mathrm{\Delta }}_a$ is determined:

(7)

$h_a=h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}.$

3.1. Conventional linear approximation of dry friction

It is assumed that:

(8)

$C=\left\{\begin{array}{l}\frac{h}{\mathrm{\Delta }},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|<\mathrm{\Delta }+{\mathrm{\Delta }}_a,\\ -\frac{h}{\mathrm{\Delta }},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{\Delta }+{\mathrm{\Delta }}_a\le \left|\dot{u}\right|<\mathrm{\Delta }+2{\mathrm{\Delta }}_a,\\ 0,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|\ge \mathrm{\Delta }+2{\mathrm{\Delta }}_a.\end{array}\right.$

The following parameters of the investigated structure are assumed: $\omega =$ 1, $h=$ 1.6, $\mathrm{\Delta }=$ 0.8, ${\mathrm{\Delta }}_a=$ 0.8, $c=$ 0.1, $P=$ 4, $m=$ 1, $k=$ 1$.$ Calculations from zero initial conditions are performed and two periods of steady state motions are represented in Fig. 3.

Fig. 3. Steady state motion for linear approximation of dry friction

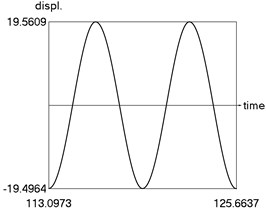
a) Displacement as function of time

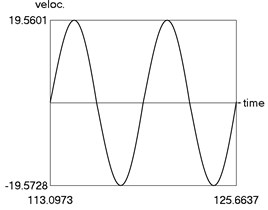
b) Velocity as function of time

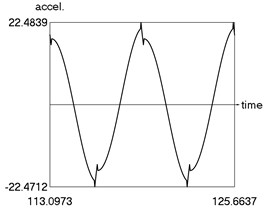
c) Acceleration as function of time

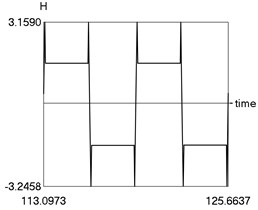
d)$H$ as function of time

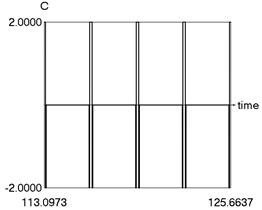
e)$C$ as function of time

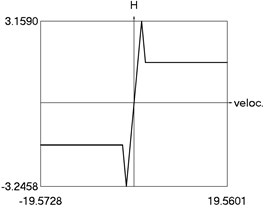
f)$H$ as function of velocity

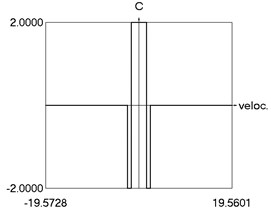
g)$C$ as function of velocity

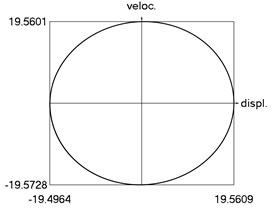
h) Phase trajectory: velocity as function of displacement

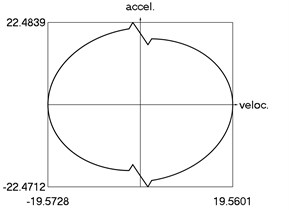
i) Phase trajectory: acceleration as function of velocity

3.2. Trigonometric approximation of dry friction

It is assumed that:

(9)

$C=\left\{\begin{array}{l}\frac{d}{d\dot{u}}\left(\left(h+h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}\right)\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi }{2}\frac{\dot{u}}{\mathrm{\Delta }+{\mathrm{\Delta }}_a}\right)=\left(h+h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}\right)\frac{\pi }{2}\frac{1}{\mathrm{\Delta }+{\mathrm{\Delta }}_a}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi }{2}\frac{\dot{u}}{\mathrm{\Delta }+{\mathrm{\Delta }}_a},\left|\dot{u}\right|<\mathrm{\Delta }+{\mathrm{\Delta }}_a,\\ \begin{array}{l}\begin{array}{l}\frac{d}{d\dot{u}}\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}-\frac{1}{2}h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi }{2}\frac{\dot{u}-\left(\mathrm{\Delta }+1.5{\mathrm{\Delta }}_a\right)}{0.5{\mathrm{\Delta }}_a}\right)=-\frac{1}{2}h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}\frac{\pi }{2}\frac{1}{0.5{\mathrm{\Delta }}_a}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi }{2}\frac{\dot{u}-\left(\mathrm{\Delta }+1.5{\mathrm{\Delta }}_a\right)}{0.5{\mathrm{\Delta }}_a},\\ \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{\Delta }+{\mathrm{\Delta }}_a\le \left|\dot{u}\right|<\mathrm{\Delta }+2{\mathrm{\Delta }}_a,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\dot{u}>0,\end{array}\\ \begin{array}{l}\frac{d}{d\dot{u}}\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}-\frac{1}{2}h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi }{2}\frac{\dot{u}+\left(\mathrm{\Delta }+1.5{\mathrm{\Delta }}_a\right)}{0.5{\mathrm{\Delta }}_a}\right)=-\frac{1}{2}h\frac{{\mathrm{\Delta }}_a}{\mathrm{\Delta }}\frac{\pi }{2}\frac{1}{0.5{\mathrm{\Delta }}_a}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi }{2}\frac{\dot{u}+\left(\mathrm{\Delta }+1.5{\mathrm{\Delta }}_a\right)}{0.5{\mathrm{\Delta }}_a},\\ \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{\Delta }+{\mathrm{\Delta }}_a\le \left|\dot{u}\right|<\mathrm{\Delta }+2{\mathrm{\Delta }}_a,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\dot{u}<0,\end{array}\end{array}\\ 0,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left|\dot{u}\right|\ge \mathrm{\Delta }+2{\mathrm{\Delta }}_a.\end{array}\right.$

Calculations from zero initial conditions are performed and two periods of steady state motions are represented in Fig. 4.

The obtained results demonstrate a higher precision of trigonometric approximation of the dry friction. This is especially evident from the indicated minimum and maximum values of $H$.

Fig. 4. Steady state motion for trigonometric approximation of dry friction

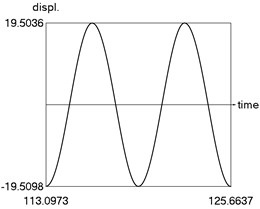
a) Displacement as function of time

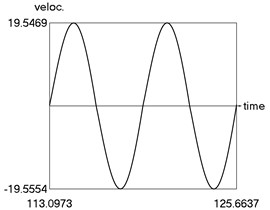
b) Velocity as function of time

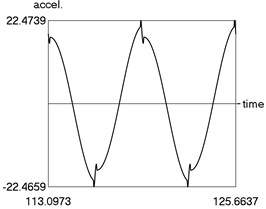
c) Acceleration as function of time

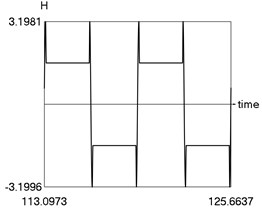
d) H as function of time

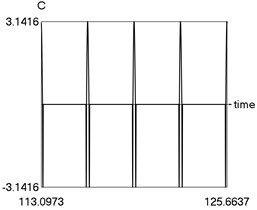
e) C as function of time

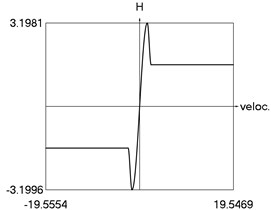
f) H as function of velocity

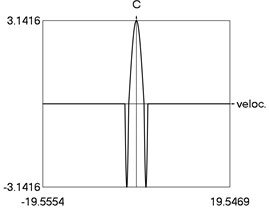
g) C as function of velocity

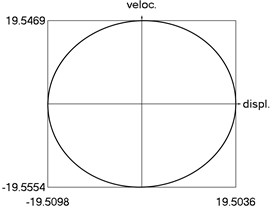
h) Phase trajectory: velocity as function of displacement

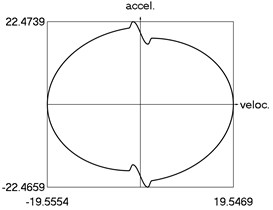
i) Phase trajectory: acceleration as function of velocity

4. Conclusions

In the numerical investigation of vibration problems with dry friction it is accepted to use some type of approximation to this phenomenon. Often linear variation of the force of friction in a region around zero velocity is assumed. In this paper, a trigonometric variation of the force of friction in a region around zero velocity is proposed, and the comparison of numerical results is presented. The obtained results do show a higher precision of the proposed approximation.

Investigation of the problem with more complicated dry friction phenomenon is also performed. The increase of the coefficient of dry friction near to the value of zero velocity is assumed. This model confirms the conclusions obtained previously for the simplest model of dry friction.

The advantage of the investigated models of dry friction when compared to some other known approximate models is in the fact that they have a local transition region near to the value of zero velocity.

Acknowledgements

References

1. Levy S., Wilkinson J. P. D. The Component Element Method in Dynamics with Application to Earthquake and Vehicle Engineering. McGraw-Hill, New York, 1976. [Search CrossRef]
2. Ragulskienė V. Vibro-Shock Systems (Theory and Applications). Mintis, Vilnius, 1974, (in Russian). [Search CrossRef]
3. Bolotin V. V. Vibrations in Engineering. Handbook, Vol. 1, Mashinostroienie, Moscow, 1978, (in Russian). [Search CrossRef]
4. Inman D. J. Vibration with Control, Measurement, and Stability. Prentice-Hall, New Jersey, 1989. [Search CrossRef]
5. Lalanne M., Berthier P., der Hagopian J. Mechanical Vibrations for Engineers. John Wiley and Sons, New York, 1984. [Search CrossRef]
6. Thomson W. T. Theory of Vibration with Applications. Prentice-Hall, New Jersey, 1981. [Search CrossRef]
7. Bathe K. J. Finite Element Procedures in Engineering Analysis. Prentice-Hall, New Jersey, 1982. [Search CrossRef]
8. Sumbatov A. S., Yunin Ye. K. Selected Problems of Mechanics of Systems with Dry Friction. Physmathlit, Moscow, 2013, (in Russian). [Search CrossRef]
9. Kohli R., Mittal Kashmiri L. Developments in Surface Contamination and Cleaning: Methods for Surface Cleaning., Elsevier, 2016. [Search CrossRef]
10. Chahine G. L., Kapahi A., Choi J.-K., Hsiao Ch.-T. Modeling of surface cleaning by cavitation bubble dynamics and collapse. Ultrasonics Sonochemistry, Vol. 29, 2016, p. 528-549. [Search CrossRef]
11. Witte A. K., Bobal M., David R., Blättler B., Schoder D., Rossmanith P. Investigation of the potential of dry ice blasting for cleaning and disinfection in the food production environment. LWT – Food Science and Technology, Vol. 75, 2016, p. 735-741. [Search CrossRef]
12. Mažeika D., Ragulskis K., Kandrotaitė-Janutienė R., Bubulis A., Bartkus A. Cleaning of the surface contaminated by micro-particles by means of vibrations. Vibroengineering Procedia, Vol. 7, 2016, p. 65-69. [Search CrossRef]
13. Petean P. G. C., Aguiar M. L. Determination of the adhesion force between particles and rough surfaces. Powder Technology, Vol. 274, 2015, p. 67-76. [Search CrossRef]
14. Cui Y., Sommerfield M. Forces on micron-sized particles randomly distributed on the surface of larger particles and possibility of detachment. International Journal of Multiphase Flow, Vol. 72, 2015, p. 39-52. [Search CrossRef]
15. Jiang Y., Turner K. T. Measurement of the strength and range of adhesion using atomic force microscopy. Extreme Mechanics Letters, Vol. 9, Issue 1, 2016, p. 119-126. [Search CrossRef]
16. Kumar N., Zhao C., Klaassen A., Van Den Ende D., Mugele F., Siretanu I. Characterisation of the surface charge distribution on kaolinite particles using high resolution atomic force microscopy. Geochimica et Cosmochimica Acta, Vol. 175, 2016, p. 100-112. [Search CrossRef]
17. Pauliukaitis D., Kibirkštis E., Ragulskis K. Problems of precise vibromechanics and vibroengineering. Vibroengineering Procedia, Vol. 8, 2016, p. 377-385. [Search CrossRef]
18. Ragulskis K., Bubulis A., Mažeika D., Kandrotaitė-Janutienė R., Ragulskis L., Bartkus A. Vibrational method of cleaning of surfaces from homogeneous waste materials. Journal of Vibroengineering, Vol. 19, Issue 3, 2017, p. 1709-1717. [Search CrossRef]

Cited By