Abstract
In this work, the problem of free longitudinal vibration of rods with variable cross-sectional area and material properties is investigated using the pseudospectral method. With the gradation of material properties like modulus of elasticity and mass density in the axial direction, the results corresponding to a functionally graded axial bar are obtained using the proposed pseudospectral formulation. The pseudospectral formulation used is relatively easy to implement and powerful in analyzing vibration problems. With the help of several numerical examples, the non-dimensional natural frequencies of rods obtained using the pseudospectral method are compared with those obtained by the analytical solution, generalized finite element method, the discrete singular convolution method and differential transformation method. The numerical results obtained show that the proposed technique allows boundary conditions to be incorporated easily and yields results with good accuracy and faster convergence rates than other methods.
1. Introduction
Functionally graded (FG) material structures find extensive use in modern engineering as their material properties can be tailored to meet the requirements of different applications [1]. The FG axial bars are a class of inhomogeneous rods/bars with material properties varying continuously in desired spatial directions. The inhomogeneous rods are known to provide a suitable distribution of strength and weight for engineering structures [2]. A study of the vibration characteristics of these rods is a subject of considerable scientific interest that has wide applications in aerospace, civil and mechanical engineering [3-5].
The governing differential equations of motion for longitudinal vibration of non-uniform rods have variable coefficients introduced by variable cross-sectional area. In addition, for functionally graded tapered axial bars, the varying material properties add up to the previous variable coefficients in the governing equation increasing the complexity in vibration analysis of these bars/rods. In general, methods of vibration analysis are classified as analytical and numerical methods while some are semi-analytical that use a combination of both the approaches. It is generally agreed that obtaining analytical/closed-form solutions of this vibration problem is possible only for some specific geometric and material functions and are often cumbersome. Application of numerical methods becomes essential to obtain the solution of the problem for general cases. There are many different methods for the numerical solution of differential equations which include Finite Element Method (FEM), Differential Quadrature Method (DQM), Differential Transformation Method (DTM), Discrete Singular Convolution (DSC) method and Spectral/Pseudo Spectral methods. Several studies have been dedicated to the problem of exact/analytic solutions for longitudinal vibrations of non-uniform rods [6-13] while some researchers [3, 14-17] have developed numerical methods.
Eisenberger [6] obtained the exact longitudinal vibration of a rod with polynomial variation in the cross-sectional area and mass distribution along the member employing an exact element method. Bapat [7] introduced an efficient approach to solve the vibration problem of a rod composed of uniformly tapered sections and studied the vibrations of a rod composed of uniform, conical, exponential and catenoidal tapers. Abrate [8] has shown that there is a class of non-uniform rods for which the equations of motion can be transformed into the wave equation and considered area of variation of the form . Kumar and Sujith [9] obtained exact analytical solutions for the longitudinal vibration of rods with polynomial and sinusoidal area variations of form , Li [10] carried out a functional transformation of the governing differential equation and presented the exact solutions for certain functional forms of an involved parameter. The differential transformation method was used in [11] to obtain exact solutions of the free axial vibration of a tapered bar with linearly varying mass and area. Raj and Sujith [12] derived a general analytical technique that helps in obtaining cross-sectional area variations which give specific, closed-form solutions for the longitudinal vibration of rods and have presented numerical solution for area variation of the form , . Yardimoglu and Aydin [13] obtained the exact longitudinal vibration characteristics of rods with sinusoidal area cross-sections of the form , in terms of associated Legendre functions. In [14], a domain partition power series method for the vibration analysis of variable cross-section rods is presented and the longitudinal vibrations of a rod with linearly varying area is studied. The differential quadrature method was used in [15] to analyze the free vibrations of a general non-uniform rod. In [16], the free vibration analysis of elastic rods was investigated using a novel global collocation method. An adaptive generalized finite element (GFEM) method was proposed in [17] to study the free longitudinal vibration analysis of straight bars and trusses. The results obtained using GFEM for sinusoidal and polynomial area variations of rod were compared with those obtained using finite element and composite elements methods. Several closed form solutions have been derived by the semi-inverse method for the problem of determining eigenvalues of inhomogeneous structures in [18]. It is also shown in [19] than an inhomogeneous rod can possess an exponential mode shape and derived closed-form solutions that can be utilized as model solutions for verification purposes. Recently, [3] investigated the longitudinal free vibrations of non-uniform rods by using the Discrete Singular Convolution (DSC) approach. The non-dimensional natural frequencies, obtained were compared with those obtained using exact methods and the differential quadrature method.
In most of the aforementioned works, the focus was on vibration of rods having variable area cross-sections. Recently, the longitudinal vibration of a functionally graded tapered axial bar was considered in [20] wherein, the material gradation was accounted for by varying the modulus of elasticity and mass density. Two new approaches based on Differential Transformation Method (DTM), namely Differential Transform Element Method (DTEM) and Differential Quadrature Element method of Lowest order (DQEL) were introduced by them to numerically study the free longitudinal vibration of tapered functionally graded (FG) rods. Further, in [21], the longitudinal vibrations of a linearly tapered axial bar with exponential variation in mass density and modulus of elasticity was investigated using Finite Element Method (FEM) by proposing a new element that could be derived by using the basic principles of structural mechanics.
The purpose of this paper is to implement the pseudospectral method for the longitudinal vibration analysis of tapered axial bars. Pseudospectral methods (PSM) are powerful tools for solving differential equations with high accuracy in a simple domain. The method has been successfully applied to the free vibration analysis of curved Timoshenko beams [22], Timoshenko beams and axisymmetric Mindlin plates [23], linear and non-linear beams [24], cylindrical helical springs [25] and Functionally graded Timoshenko beams [26]. There have been different approaches in implementing the pseudospectral formulations based on their treatment of boundary conditions. In this work, an efficient formulation of the PSM involving a change of independent variable that greatly simplifies computer programs for solving differential equations is used to transform the governing differential equation together with the boundary conditions into an eigenvalue problem, in which the eigenvalue represents the physical property of the vibration problem, namely the natural frequency. The problem is then solved using standard eigensolvers. The remainder of the paper is organized as follows. In Section 2, we introduce the pseudospectral method. In Section 3, we outline the problem and the solution methodology. In Section 4, the method is applied to examples that outline the convergence behavior, perform validations and demonstrate the advantages of the method.
2. Pseudospectral method
The spectral methods arise from the fundamental problem of approximation of a function by interpolation on an interval and are very much successful for the numerical solution of differential equations [27]. The PS method can be considered as a spectral method that performs a collocation process and delivers exponential (spectral) accuracy under the condition of smoothness. The starting point for the Pseudospectral method is the representation of the approximate solution of the solution of the given differential equation by a linear combination of basis functions :
The best choice for are the eigenfunctions of a singular Sturm-Liouville problem such as the Chebyshev polynomials. Although the Legendre, Hermite and Laguerre polynomials are eigenfunctions of Sturm-Liouville problem, Chebyshev polynomials are more effective in handling the boundaries [28]. The Chebyshev polynomials are recursive orthogonal polynomials that can be defined as:
where is an integer [29]. Although defined for all , Chebyshev polynomials are a stable representation only on .
In PS method, one is usually content with obtaining an approximation to the solution on a discrete set of grid points. The PS method, demands that the differential equation be exactly satisfied at these set of points known as collocation points [30]. The accuracy, stability and rate of convergence of the numerical solutions depend on the choice of the collocation point [31] and the best choice for the collocation points is to use nodes that are clustered near the edges of the interval with an asymptotic density proportional to as [32]. The Chebyshev polynomial extreme points that are the Chebyshev-Gauss-Lobatto sampling grid points on are known to have such density properties [33]. Therefore, these points are chosen as collocation points in this work. The internal points which are the extrema of are given by:
with denoting the end points and 1, 2, …, the internal points. These points correspond to:
The pseudospectral method associates the grid of collocation points with the basis set and the coefficients in the expansion (1) are found by requiring the residual function where is the operator of the differential equation to vanish at the collocation points. There are several ways of implementing the PS method of which the differentiation based formulation [34, 35], integration based formulation [36, 37] and straight forward implementation [22, 23] are normally used. The differentiation based formulation is widely used in which one can construct the differentiation matrices using the recurrence finite-differences formulae on arbitrarily spaced grids [34, 38] or utilizing the approach followed in [35, 39]. However, incorporation of boundary conditions when using differentiation matrices is complicated. The present work utilizes the straight forward implementation utilizing the Chebyshev polynomial-to-cosine change of variable together with a proper selection of internal collocation points based on the boundary conditions.
3. Mathematical formulation and solution methodology
The differential equation that governs the free longitudinal vibration of a axially graded bar reads as [40]:
Here denotes the axial coordinate, denotes longitudinal displacement at any position and time . , and are the modulus of elasticity, cross-sectional area and mass density respectively, which are assumed to vary along the axial coordinate with and being the end coordinates of the rod. The classical boundary conditions considered are:
The longitudinal displacement is assumed to be separable in space and time where the time dependence is harmonic with angular frequency i.e., where represents the mode shape. Denote where is the axial rigidity that varies along the axial coordinate .
Eq. (5) becomes :
where:
The governing equation becomes:
We now outline the solution methodology for Eq. (8) using PSM. The natural interval in which the collocation points are located may be adapted to the interval of interest by the transformation:
where .
Due to change of variable:
Applying the transformation, the solution function is now a function of and is assumed to be of the form:
Here:
It is to be noticed that the trigonometric form of the Chebyshev polynomial which is a change of coordinate is used for the representation of the approximate solution. This is coupled with analytic differentiation and collocation at internal points followed by enforcement of boundary conditions at end points.
The transformed governing differential equation is:
If we collocate Eq. (17) at the points given by Eq. (4) and enforce the boundary conditions at 0, which are given by:
Then we get a system of equations that is expressed as a matrix eigen value equation. The resulting equation is then solved using a standard eigensolver.
4. Numerical results and discussion
In this section we examine the convergence behavior of the PS method, validate the accuracy by comparing the results obtained with other analytical/numerical methods. Finally, we apply the method to obtain the non-dimensional frequencies of vibration of a functionally graded axial bar. In all the examples considered, the rods are of unit length. The details of the work carried out in this section are presented in Table 1. A diagrammatic view of typical rods considered herein is given in Fig. 1.
Table 1A layout of the numerical work carried out in Section 4
Purpose | Section | Variable characteristics of rod | End conditions | Previous literature (used for comparison) | |
, | Method | Reference number | |||
Convergence behaviour study | 4.1 | 1. | Fixed-Free | Analytical | [8] |
2. ; | Free-Fixed | Differential transform | [11] | ||
3. | Fixed-Fixed and Fixed-Free | Discrete singular convolution | [3] | ||
Validation of accuracy | 4.2 | and | Fixed-Fixed | Analytical and generalized FEM | [9, 17] |
4.3 | Fixed-Fixed and Fixed-Free | Analytical | [13] | ||
4.4 | and | Fixed-Fixed, Fixed-Free and Fixed-Fixed | Analytical | [12] | |
4.5 | 1. | Fixed-Free and Fixed-Fixed | DQEL/ DTEM | [20] | |
2. and | Fixed-Free and Fixed-Fixed | FEM with a new element | [21] | ||
4.1. Convergence behaviour of PS method
To study the convergence behaviour of the PS method in obtaining the frequency values of the vibration of non-uniform rods, some examples have been examined. As a first example, we consider the longitudinal free vibration of a fixed-free non-uniform bar with polynomial variation of cross-section area, constant elasticity modulus and constant density and unit length. The cross-section area varies as where is a reference cross-section area. Abrate [8] has presented exact analytical solution for longitudinal free vibration of bars with polynomial area variations. The exact non-dimensional frequency parameters of rods given [8] are set as basis values and the relative error of the PS method with values varying from 10 to 16 is analyzed. The relative errors of the numerical values of the first six non-dimensional natural frequencies given by ; computed using the PS method are presented in Table 2. It is observed that the proposed method requires less number of grid points to obtain a relative error of the order of 10-5 in the computation of the first six non-dimensional frequency values of a non-uniform rod with polynomial variation of cross section area.
As a second example we examine the convergence of the PS method by considering the free axial vibration of a tapered fixed-free bar. The area of cross-section and mass density are assumed to vary linearly i.e. and where is the characteristic area and the characteristic mass. The computations are carried out for a unit length rod. The exact first two non-dimensional frequency values given in [11] are taken as basis values and the relative error of the PS method with varying from 6 to 9 are presented in Table 3. It is observed that the present method achieves a relative error of order 10-6 with fewer grid points.
Fig. 1A Schematic view of typical inhomogeneous rods
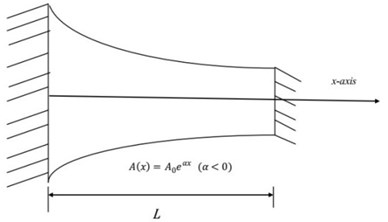
a) Fixed-Fixed non-uniform exponential rod
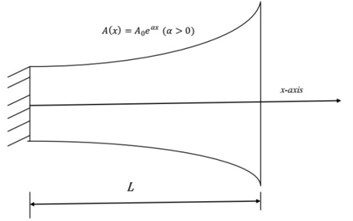
b) Fixed-Free non-uniform exponential rod
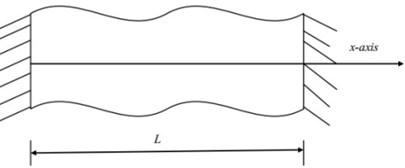
c) Fixed-Free non-uniform sinusoidal rod
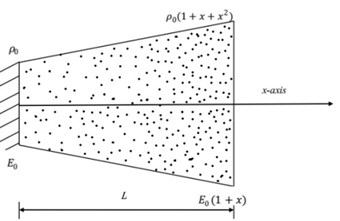
d) Side view of axially graded fixed-free bar
Table 2Convergence study of non-uniform fixed free rods with Ax=A01+2x2
Mode | Non dimensional frequency values Abrate [8] | Relative errors | |||
10 | 12 | 14 | 16 | ||
1 | 0.967403 | 3.976E-05 | 3.7 E-06 | 6.512 E-07 | 4.031 E-07 |
2 | 4.567452 | 3.027 E-06 | 1.860 E-07 | 4.816 E-08 | 3.721 E-08 |
3 | 7.768373 | 1.888 E-05 | 4.003 E-07 | 5.535 E-08 | 4.427 E-08 |
4 | 10.934682 | 6.278 E-04 | 3.47 E-05 | 1.415 E-06 | 9.145 E-09 |
5 | 14.089887 | 2.545 E-03 | 2.346 E-05 | 1.675 E-05 | 8.928 E-07 |
6 | 17.240109 | 1.525E-02 | 3.22 E-04 | 3.22 E-04 | 2.700 E-05 |
Table 3Convergence study of tapered fixed free rod with Ax=2A0x and m(x)=2m0x
Mode | Non dimensional frequency values Zang and Bert [11] | Relative errors | |||
6 | 7 | 8 | 9 | ||
1 | 2.4048 | 8.316E-05 | 8.316E-06 | 8.316E-06 | 8.316E-06 |
2 | 5.5201 | 1.105E-04 | 3.623 E-06 | 3.623 E-06 | 3.623 E-06 |
We further study the convergence of the frequency values obtained for fixed-fixed and fixed-free non-uniform rods with cross-section area given by. We examine our results with the non-dimensional frequency values presented in [3] as basis values. Using the four digit DSC results that were computed in [3] with 500 grid points for a unit length rod, the relative error of the PS method for fixed-fixed and fixed-free rods with taking values 20, 22, 25 and 28 is presented in Table 4. The relative errors of the non-dimensional frequency parameter given by for the first 13 modes are given in the table. It is observed that precision of the order of 10-5 is obtained for all the 13 modes with 28 (29 collocation points).
4.2. Comparison with GFEM
In this example, the longitudinal free vibration of a fixed-fixed non-uniform rod with area variation given by where is a reference cross-section area is analyzed and the non-dimensional frequencies obtained using PS method are compared with the corresponding results obtained using GFEM method.
Table 4Convergence study of nonuniform rod with Ax=x-0.5exp(-0.5x2)
Boundary condition | Mode | Shokrollahi and Nejad DSC [3] 500 | Relative errors | |||
25 | 20 | 22 | 28 | |||
Fixed-Fixed | 1 | 3.4662 | 2.452 E-05 | 4.298 E-05 | 3.346 E-05 | 1.875 E-05 |
2 | 6.6399 | 1.506 E-05 | 3.991 E-05 | 2.725 E-05 | 7.379 E-06 | |
3 | 9.7930 | 2.460 E-05 | 5.483 E-05 | 3.941 E-05 | 1.552 E-05 | |
4 | 12.9405 | 3.013 E-05 | 6.460 E-05 | 4.706 E-05 | 1.962 E-05 | |
5 | 16.0857 | 3.577 E-05 | 7.397 E-05 | 5.427 E-05 | 2.374 E-05 | |
6 | 19.2297 | 3.879 E-05 | 8.066 E-05 | 5.938 E-05 | 2.605 E-05 | |
7 | 22.3730 | 4.116 E-05 | 8.671 E-05 | 6.351 E-05 | 2.748 E-05 | |
8 | 25.5158 | 4.115 E-05 | 8.900 E-05 | 6.454 E-05 | 2.621 E-05 | |
9 | 28.6584 | 4.428 E-05 | 1.433 E-04 | 7.048 E-05 | 2.875 E-05 | |
10 | 31.8008 | 4.767 E-05 | 4.683 E-04 | 5.330 E-05 | 3.116 E-05 | |
11 | 34.9430 | 4.538 E-05 | 4.991 E-03 | 4.781 E-04 | 3.196 E-05 | |
12 | 38.0851 | 1.016 E-04 | 1.619 E-02 | 2.423 E-03 | 3.313 E-05 | |
13 | 41.2272 | 3.379 E-04 | 2.320 E-02 | 1.234 E-02 | 4.334 E-05 | |
Fixed-Free | 1 | 2.1954 | 3.006 E-05 | 2.960 E-05 | 2.505 E-05 | 1.776 E-05 |
2 | 5.2032 | 2.229 E-05 | 5.169 E-05 | 3.939 E-05 | 2.037 E-05 | |
3 | 8.3081 | 2.864 E-05 | 5.067 E-05 | 3.755 E-05 | 1.709 E-05 | |
4 | 11.4328 | 2.212 E-05 | 5.886 E-05 | 4.163 E-05 | 1.495 E-05 | |
5 | 14.5648 | 3.199 E-05 | 6.495 E-05 | 4.689 E-05 | 1.881 E-05 | |
6 | 17.7002 | 3.581 E-05 | 7.926 E-05 | 5.819 E-05 | 2.547 E-05 | |
7 | 20.8374 | 3.978 E-05 | 7.976 E-05 | 5.907 E-05 | 2.495 E-05 | |
8 | 23.9757 | 3.870 E-05 | 7.741 E-05 | 6.460 E-05 | 2.594 E-05 | |
9 | 27.1148 | 4.329 E-05 | 1.339 E-04 | 5.934 E-05 | 2.714 E-05 | |
10 | 30.2544 | 4.657 E-05 | 5.397 E-04 | 1.979 E-05 | 3.001 E-05 | |
11 | 33.3944 | 6.444 E-05 | 4.309 E-04 | 1.366 E-04 | 3.129 E-05 | |
12 | 36.5346 | 1.083 E-05 | 1.925 E-03 | 1.518 E-03 | 2.923 E-05 | |
13 | 39.6750 | 1.698 E-04 | 7.268 E-03 | 6.095 E-04 | 4.398 E-05 | |
Table 5Comparison of non-dimensional frequencies of fixed-fixed non-uniform rods
Variation in area | Mode | Kumar and Sujith [9] | Adaptive GFEM Arndt et al. [17] | PS method 16 |
Polynomial | 1 | 3.286007 | 3.286007 | 3.286007 |
2 | 6.360678 | 6.360678 | 6.360678 | |
3 | 9.477196 | 9.477196 | 9.477196 | |
4 | 12.605890 | 12.605890 | 12.605890 |
The GFEM method is an iterative approach whose main goal is to increase the accuracy of eigenvalues related to a chosen vibration mode. In the method [17] each tangent frequency was obtained by different iterative analysis. The results presented in [17] brought out the narrow precision of GFEM than the c-version of composite element method and the -version of FEM in free longitudinal vibration analysis of uniform and non-uniform straight bars for the same degree of freedom. For the considered example, the results of the PS method have been obtained using 16 (17 collocation points). Table 5 presents the first four non-dimensional eigenvalues obtained by these methods. The results show that the PS method which is easier and simple to implement achieves the same accuracy as that of the adaptive GFEM with relatively few grid points.
4.3. Rods with sinusoidal variation of cross-section area
A numerical study of the longitudinal vibrations of non-uniform rods with area variations of the form is carried out. The non-dimensional eigenvalues are computed with 29 (i.e. 30 collocation points) for various parameter (, , ) values under different boundary conditions and the lowest six eigenvalues for each end conditions are listed in the tables. The non-dimensional frequencies of fixed-fixed and fixed-free non-uniform rods with variation in area given by , , 1 for 1, 2, 3, 4 is computed. The computations have been carried out with 29 (30 collocation points) to obtain a precision of 6 digits. The results obtained are given in Tables 6 and 7 and are found to be in good agreement with the exact results obtained by [13].
Table 6Non-dimensional natural frequencies of fixed-fixed rods with Ax=A0sinnax+b, a=π-2b, b= 1
1 | 2 | 3 | 4 | |||||
Mode | Yardimoglu and Aydin [13] | PS method | Yardimoglu and Aydin [13] | PS method | Yardimoglu and Aydin [13] | PS method | Yardimoglu and Aydin [13] | PS method |
1 | 3.033658 | 3.0336576 | 2.926836 | 2.9268362 | 2.821246 | 2.8212460 | 2.717003 | 2.7170029 |
2 | 6.228475 | 6.2284746 | 6.178607 | 6.1786069 | 6.133696 | 6.1336963 | 6.093840 | 6.0938397 |
3 | 9.388171 | 9.3881713 | 9.355384 | 9.3553837 | 9.326456 | 9.3264558 | 9.301424 | 9.3014242 |
4 | 12.538877 | 12.5388771 | 12.514409 | 12.5144091 | 12.492985 | 12.4929848 | 12.474621 | 12.4746212 |
5 | 15.685954 | 15.6859536 | 15.666425 | 15.6664251 | 15.649387 | 15.6493872 | 15.634849 | 15.6348492 |
6 | 18.831208 | 18.8312077 | 18.814955 | 18.8149548 | 18.800803 | 18.8008028 | 18.788757 | 18.7887572 |
Table 7Non-dimensional natural frequencies of clamped-free (fixed-free) rods with
, , 1 | ||||||||
1 | 2 | 3 | 4 | |||||
Mode | Yardimoglu and Aydin [13] | PS method | Yardimoglu and Aydin [13] | PS method | Yardimoglu and Aydin [13] | PS method | Yardimoglu and Aydin [13] | PS method |
1 | 1.568123 | 1.5681231301 | 1.560155 | 1.5601546708 | 1.547041 | 1.5470412314 | 1.529023 | 1.5290233495 |
2 | 4.715830 | 4.7158295684 | 4.726102 | 4.7261023944 | 4.743064 | 4.7430637298 | 4.766484 | 4.7664838791 |
3 | 7.856372 | 7.8563718913 | 7.863537 | 7.8635367860 | 7.875459 | 7.8754586693 | 7.892108 | 7.8921080766 |
4 | 10.997350 | 10.9973504866 | 11.002678 | 11.0026777710 | 11.011552 | 11.0115521944 | 11.023967 | 11.0239671552 |
5 | 14.138571 | 14.1385710137 | 14.142783 | 14.1427828065 | 14.149801 | 14.1498010423 | 14.159624 | 14.1596235881 |
6 | 17.279918 | 17.2799178393 | 17.283392 | 17.2833923984 | 17.289183 | 17.2891827469 | 17.297288 | 17.2972880091 |
4.4. Rods with exponential variation of cross-section area
In this section, the variation in the natural frequencies of rod with exponential area variation of the forms and are analyzed. The length of the rod is considered to be one unit with 0.1 units and 1.1 units as in [12]. The fundamental frequencies for fixed-fixed and fixed-free rods are computed using PS method for –2.5, –2.0, –1.5, –0.5, 0.5, 1.0, 1.5, 2.0, 2.5 and –3, –1, 1 and 3 in the first area variation. A comparison of the values obtained is carried out with the corresponding the exact values in [12]. The frequency values with 6 significant digits for the three end conditions are given in Tables 8, 9 and have been obtained using 29. The results bring out the accuracy of the method. Now, consider a fixed-fixed non-uniform rod with area variation given by The natural frequencies for different values of the parameters are given in Table 10. The fundamental, first overtone and second overtone frequency values obtained using the PS method are presented in the tables for –2.5, –1.5, –0.5, 0.5, 1.5, 2.5 and –3, –1, 1 and 3. These values are presented along with the corresponding exact values given in [12]. Though exact values are available for 3 significant digits, the approximate values are given for 6 significant digits for future comparison. It is observed from the results that the proposed PS formulation achieves good accuracy/convergence with less computational effort.
Table 8Fundamental frequency values for fixed-fixed rods with Ax=Kxnexp(bx2)
–3 | –1 | 1 | 3 | |||||
Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | |
–2.5 | 5.286 | 5.286487 | 4.608 | 4.607728 | 4.270 | 4.269796 | 4.353 | 4.352809 |
–2.0 | 4.885 | 4.884997 | 4.280 | 4.278711 | 4.038 | 4.038238 | 4.226 | 4.226488 |
–1.5 | 4.471 | 4.471088 | 3.949 | 3.948826 | 3.820 | 3.820109 | 4.122 | 4.121969 |
–0.5 | 3.622 | 3.622149 | 3.317 | 3.316916 | 3.464 | 3.464380 | 4.015 | 4.014968 |
0.0 | 3.206 | 3.205804 | 3.043 | 3.043136 | 3.356 | 3.355694 | 4.034 | 4.034498 |
0.5 | 2.817 | 2.816767 | 2.825 | 2.825281 | 3.314 | 3.313942 | 4.115 | 4.115115 |
1.0 | 2.479 | 2.479202 | 2.686 | 2.686375 | 3.349 | 3.349120 | 4.260 | 4.259864 |
1.5 | 2.221 | 2.221301 | 2.642 | 2.642387 | 3.462 | 3.461533 | 4.465 | 4.464770 |
2.0 | 2.068 | 2.068134 | 2.695 | 2.694565 | 3.642 | 3.641521 | 4.720 | 4.719870 |
2.5 | 2.030 | 2.029770 | 2.829 | 2.828769 | 3.873 | 3.873233 | 5.012 | 5.011982 |
3.0 | 2.094 | 2.094091 | 3.023 | 3.022737 | 4.140 | 4.139679 | 5.328 | 5.327778 |
Table 9Fundamental frequency values for fixed-free rods with Ax=Kxnexp(bx2)
–3 | –1 | 1 | 3 | |||||
Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | |
–2.5 | 4.884 | 4.883958 | 3.738 | 3.737838 | 2.638 | 2.637833 | 1.674 | 1.674235 |
–2.0 | 4.494 | 4.494413 | 3.399 | 3.398900 | 2.350 | 2.350311 | 1.447 | 1.446866 |
–1.5 | 4.089 | 4.088940 | 3.051 | 3.050617 | 2.061 | 2.060792 | 1.226 | 1.225409 |
–0.5 | 3.233 | 3.233094 | 2.330 | 2.330227 | 1.485 | 1.484599 | 0.812 | 0.812405 |
0.0 | 2.791 | 2.790891 | 1.966 | 1.966070 | 1.207 | 1.207392 | 0.630 | 0.629796 |
0.5 | 2.350 | 2.350355 | 1.610 | 1.609937 | 0.948 | 0.947727 | 0.470 | 0.470061 |
1.0 | 1.924 | 1.923852 | 1.274 | 1.273623 | 0.715 | 0.715118 | 0.338 | 0.337307 |
1.5 | 1.525 | 1.525415 | 0.970 | 0.970008 | 0.518 | 0.517865 | 0.233 | 0.233024 |
2.0 | 1.169 | 1.168590 | 0.710 | 0.710121 | 0.359 | 0.360406 | 0.156 | 0.155565 |
2.5 | 0.864 | 0.863907 | 0.500 | 0.500186 | 0.242 | 0.242026 | 0.101 | 0.100883 |
3.0 | 0.617 | 0.616690 | 0.341 | 0.340130 | 0.158 | 0.157712 | 0.064 | 0.063935 |
4.5. Functionally graded tapered axial bar
In the first example, we consider a tapered bar with a rectangular cross-section whose breath taper ratio is height taper ratio is and whose cross-section is given by The modulus of elasticity and mass density vary as and respectively. For such an FG axial bar, Shahba and Rajasekharan [20] computed the non-dimensional frequencies using DQEL and DTEM methods. Both the methods are known to considerably improve the convergence rate of conventional Differential Transform Method (DTM). PSM is used in the present work to compute the non-dimensional longitudinal frequencies given by , () with 10 (11 collocation point) under Fixed-Free and Fixed-Fixed boundary conditions. The first three frequency values computed using the PSM method are compared with those obtained using DQEL/DTEM methods in Tables 11, 12. It is observed that the frequencies are significantly dependent on the cross-section area which is in turn dependent on both the height and breadth taper ratios. The accuracy of the proposed method is evident from the results presented in the Tables 11, 12. The ease of implementation is the added advantage.
Table 10Fundamental, first and second overtone frequency values for fixed-fixed rods with Ax=Kxnexp(bx)
Frequency | |||||||||
–3 | –1 | 1 | 3 | ||||||
Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | Raj and Sujith [12] | PS method | ||
Fundamental | –2.5 | 5.238 | 5.238527 | 4.637 | 4.637222 | 4.181 | 4.181430 | 3.921 | 3.920829 |
–1.5 | 4.551 | 4.551209 | 4.023 | 4.023155 | 3.690 | 3.689657 | 3.605 | 3.604571 | |
–0.5 | 3.835 | 3.835153 | 3.436 | 3.435609 | 3.300 | 3.300225 | 3.460 | 3.460119 | |
0.5 | 3.149 | 3.149215 | 2.979 | 2.978935 | 3.134 | 3.134029 | 3.572 | 3.572401 | |
1.5 | 2.645 | 2.644851 | 2.814 | 2.813816 | 3.280 | 3.280556 | 3.941 | 3.941452 | |
2.5 | 2.509 | 2.509226 | 3.008 | 3.007659 | 3.689 | 3.688720 | 4.473 | 4.472545 | |
First overtone | –2.5 | 8.014 | 8.013470 | 7.570 | 7.569653 | 7.234 | 7.234170 | 7.023 | 7.022754 |
–1.5 | 7.335 | 7.335764 | 6.980 | 6.980137 | 6.754 | 6.753894 | 6.670 | 6.670355 | |
–0.5 | 6.720 | 6.719940 | 6.488 | 6.488146 | 6.406 | 6.405740 | 6.478 | 6.478436 | |
0.5 | 6.245 | 6.244882 | 6.170 | 6.170228 | 6.256 | 6.256576 | 6.498 | 6.497498 | |
1.5 | 5.982 | 5.981634 | 6.083 | 6.082643 | 6.342 | 6.341725 | 6.740 | 6.740350 | |
2.5 | 5.965 | 5.964897 | 6.237 | 6.237472 | 6.650 | 6.649665 | 7.176 | 7.176343 | |
Second overtone | –2.5 | 10.858 | 10.859154 | 10.511 | 10.510870 | 10.248 | 10.247762 | 10.077 | 10.076690 |
–1.5 | 10.249 | 10.248726 | 9.985 | 9.984917 | 9.816 | 9.816274 | 9.748 | 9.747800 | |
–0.5 | 9.743 | 9.742691 | 9.581 | 9.581170 | 9.523 | 9.522504 | 9.568 | 9.568586 | |
0.5 | 9.386 | 9.385647 | 9.339 | 9.338701 | 9.398 | 9.398571 | 9.563 | 9.563248 | |
1.5 | 9.205 | 9.205052 | 9.278 | 9.278490 | 9.458 | 9.458103 | 9.738 | 9.737949 | |
2.5 | 9.211 | 9.211393 | 9.404 | 9.404156 | 9.697 | 9.697506 | 10.080 | 10.082356 | |
Table 11Non-dimensional frequencies of a fixed-free axially FG bar
Shahba and Rajasekaran [20] DQEL/DTEM | PS method | Shahba and Rajasekaran [20] DQEL/DTEM | PS method | Shahba and Rajasekaran [20] DQEL/DTEM | PS method | ||
0.2 | 0.2 | 1.3119 | 1.311936 | 4.2841 | 4.284133 | 7.1821 | 7.181803 |
0.4 | 1.3928 | 1.392789 | 4.3090 | 4.309044 | 7.1970 | 7.196715 | |
0.6 | 1.5059 | 1.505925 | 4.3559 | 4.355943 | 7.2260 | 7.225773 | |
0.8 | 1.6818 | 1.681840 | 4.4726 | 4.472646 | 7.3068 | 7.306703 | |
0.4 | 0.4 | 1.4759 | 1.475871 | 4.3377 | 4.337722 | 7.2143 | 7.214022 |
0.6 | 1.5917 | 1.591695 | 4.3897 | 4.389690 | 7.2466 | 7.246450 | |
0.8 | 1.7706 | 1.770668 | 4.5138 | 4.513827 | 7.3329 | 7.332918 | |
0.6 | 0.6 | 1.7104 | 1.710443 | 4.4487 | 4.448671 | 7.2839 | 7.283791 |
0.8 | 1.8918 | 1.891820 | 4.5832 | 4.583282 | 7.3787 | 7.378728 | |
0.8 | 0.8 | 2.0723 | 2.072303 | 4.7328 | 4.732920 | 7.4888 | 7.488952 |
In the second example we consider a functionally graded tapered axial bar with ; and where is the taper ratio. For such an FG axial bar Shahba et al [21] computed the nondimensional frequencies , () using Finite element method by introducing the concept of basic displacement functions. The pseudospectral method is used in the present work to compute the first three non-dimensional frequencies of the axial bar with 16 under fixed-fixed, fixed-free boundary conditions. The results obtained using the present method are compared with those presented in [21] in Table 13. It is observed from the table that the results obtained using PSM is slightly lower than that of [21]. The results presented in [21] were calculated utilizing 20 elements to model the bar for a taper ratio of 0.1 and higher number of elements for other taper ratios. Moreover, it is observed from literature [21], that the stiffness method generally provides results that are higher than the exact ones. We therefore, feel that the results obtained here are of high precision with fewer collocation points.
Table 12Non-dimensional frequencies of a fixed-fixed axially FG bar
Shahba and Rajasekaran [20] DQEL/DTEM | PS method | Shahba and Rajasekaran [20] DQEL/DTEM | PS method | Shahba and Rajasekaran [20] DQEL/DTEM | PS method | ||
0.2 | 0.2 | 2.8539 | 2.853926 | 5.7515 | 5.751501 | 8.6378 | 8.637841 |
0.4 | 2.8369 | 2.836936 | 5.7430 | 5.742966 | 8.6321 | 8.632147 | |
0.6 | 2.8042 | 2.804223 | 5.7260 | 5.726023 | 8.6207 | 8.620747 | |
0.8 | 2.7311 | 2.731119 | 5.6829 | 5.682900 | 8.5903 | 8.590337 | |
0.4 | 0.4 | 2.8260 | 2.825973 | 5.7375 | 5.737498 | 8.6284 | 8.628504 |
0.6 | 2.8016 | 2.801561 | 5.7249 | 5.724929 | 8.6200 | 8.620056 | |
0.8 | 2.7415 | 2.741519 | 5.6892 | 5.689170 | 8.5947 | 8.594748 | |
0.6 | 0.6 | 2.7886 | 2.788644 | 5.7188 | 5.718775 | 8.6160 | 8.615999 |
0.8 | 2.7468 | 2.746813 | 5.6942 | 5.694204 | 8.5986 | 8.598631 | |
0.8 | 0.8 | 2.7340 | 2.734041 | 5.6901 | 5.690056 | 8.5965 | 8.596521 |
Table 13Non-dimensional frequencies of a FG tapered axial bar
Taper ratio () | Fixed-Fixed | Fixed-Free | ||
Shahba et al. [21] | PS Method ( 16) | Shahba et al. [21] | PS method ( 16) | |
0.1 | 3.17567 | 3.172409 | 1.2988 | 1.2985 |
6.3247 | 6.298648 | 4.6478 | 4.637424 | |
9.5228 | 9.435093 | 7.8592 | 7.809505 | |
0.3 | 3.1514 | 3.148153 | 1.3722 | 1.371958 |
6.3123 | 6.286365 | 4.6656 | 4.655118 | |
9.5144 | 9.426885 | 7.8698 | 7.819942 | |
0.5 | 3.1120 | 3.108831 | 1.4710 | 1.470676 |
6.2916 | 6.265918 | 4.6983 | 4.687528 | |
9.5005 | 9.413135 | 7.8899 | 7.839570 | |
0.7 | 2.9780 | 2.975221 | 1.7168 | 1.716251 |
6.2113 | 6.186568 | 4.8486 | 4.836778 | |
9.4427 | 9.357079 | 7.9958 | 7.9433464 | |
5. Conclusions
The main contribution of the present study consists in applying a pseudospectral formulation for solving the governing differential equation of motion for tapered functionally graded axial bars. The method utilizes a Chebyshev polynomial-to-cosine change of variable that simplifies the computer implementation and achieves good precision. Numerical experiments that include variation in geometrical properties (area of cross-section) and/or material properties (mass density, modulus of elasticity) have been considered and the results obtained with less computational effort exhibits good accuracy and flexibility for longitudinal vibration analysis of tapered axial bars.
References
-
Elishakoff I., Pentaras D., Cristina G. Mechanics of Functionally Graded Material Structures. World Scientific, 2015.
-
Simsek M. Nonlocal effects in the free longitudinal vibration of axially functionally graded tapered nanorods. Computational Materials Science, Vol. 61, 2012, p. 254-265.
-
Shokrollahi M., Nejad A. Z. B. Numerical analysis of free longitudinal vibration of non uniform rods: discrete singular convolution approach. Journal of Engineering Mechanics, Vol. 140, 2014, p. 6014007.
-
Kapulnov J., Prikazchikov D., Sergushova O. Multi-Parametric analysis of the lowest natural frequencies of strongly inhomogeneous elastic rods. Journal of Sound and Vibration, Vol. 366, 2016, p. 264-276.
-
Li L., Hu H., Li X. Longitudinal vibration of size-dependent rods via nonlocal starch gradient theory. International Journal of Mechanical Sciences, Vol. 115, Issue 116, 2016, p. 135-144.
-
Eisenberger M. Exact longitudinal vibration frequencies of a variable cross-section rod. Applied Acoustics, Vol. 34, 1991, p. 123-130.
-
Bapat C. N. Vibration of rods with uniformly tapered sections. Journal of Sound and Vibration, Vol. 185, 1995, p. 185-189.
-
Abrate S. Vibration of non-uniform rods and beams. Journal of Sound and Vibration, Vol. 185, 1995, p. 703-716.
-
Kumar B. M., Sujith R. I. Exact solutions for the longitudinal vibration of non-uniform rods. Journal of Sound and Vibration, Vol. 207, 1997, p. 721-729.
-
Li Q. S. Exact solution for free longitudinal vibration of non-uniform rods. Journal of Sound and Vibration, Vol. 234, 2000, p. 1-19.
-
Zeng H., Bert C. W. Vibration analysis of a tapered bar by differential transformation. Journal of Sound and Vibration, Vol. 242, 2001, p. 737-739.
-
Raj A., Sujith R. I. Closed-form solutions for the free longitudinal vibrations of inhomogeneous rods. Journal of Sound and Vibration, Vol. 283, 2005, p. 1015-1030.
-
Yardimoglu B., Aydin L. Exact longitudinal characteristics of rods with variable cross-sections. Shock and Vibration, Vol. 18, 2011, p. 555-562.
-
Inaudi J. A., Matusevich A. E. Domain-partition power series in vibration analysis of variable-cross-section rods. Journal of Sound and Vibration, Vol. 329, 2010, p. 4534-4549.
-
Al Kaisy A. M. A., Esmaeel R. A., Nassar M. M. Application of the differential quadrature method in the longitudinal vibration of non-uniform rods. Engineering Mechanics, Vol. 14, 2007, p. 303-310.
-
Provatidids C. G. Free vibration analysis of elastic rods using global collocation. Archive of Applied Mechanics, Vol. 78, 2008, p. 241-250.
-
Arndt M., Machado R. D., Scremin A. An adaptive generalized finite element method applied to free vibration analysis of straight bars and trusses. Journal of Sound and Vibration, Vol. 329, 2010, p. 659-672.
-
Elishakoff I. Eigenvalues of Inhomogeneous Structures: Unusual Closed-Form Solutions. CRC Press, USA, 2005.
-
Calio I., Elishakoff I. Exponential solution for a longitudinally vibrating inhomogeneous rod. Journal of Mechanical and Material Structures, Vol. 4, 2009, p. 1251-1256.
-
Shahba A., Rajasekaran S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials. Applied Mathematical Modeling, Vol. 36, 2012, p. 3094-3111.
-
Shahba A., Attarnejad R., Hajilar Sh. A mechanical-based solution for axially functionally graded tapered Euler-Bernoulli beams. Mechanics of Advanced Materials and Structures, Vol. 20, 2013, p. 696-707.
-
Lee J. In-plane free vibration analysis of curved Timoshenko beams by the pseudospectral method. International Journal of KSME, Vol. 17, 2003, p. 1156-1163.
-
Lee J., Schultz W. W. Eigenvalue analysis of Timoshenko beams and axisymmetric Mindlin plates by the pesudospectral method. Journal of Sound and Vibration, Vol. 269, 2004, p. 609-621.
-
Yagci B., Filiz S., Romero L. L., Ozdoganlar O. B. A spectral Tchebyshev technique for solving linear and nonlinear beam equations. Journal of Sound and Vibration, Vol. 321, 2004, p. 375-404.
-
Lee J. Free vibration analysis of cylindrical helical springs by the pseudospectral method. Journal of Sound and Vibration, Vol. 302, 2007, p. 185-196.
-
Wattanasakulpong N., Mao Q. Dynamic response of Timoshenko functionally graded beams with classical and non-classical boundary conditions using Chebyshev collocation method. Composite Structures, Vol. 119, 2015, p. 346-354.
-
Canuto C., Hussaini M., Quanteroni A., Zang T. Spectral Methods in Fluid Dynamics. Springer, Berlin, 1988.
-
Gotlieb D., Orzag S. A. Numerical Analysis of Spectral Methods: Theory and Applications. SIAM, USA, 1977.
-
Mason J. C., Handscomb D. C. Chebyshev Polynomials. Chapman & Hall/CRC, USA, 2002.
-
Boyd J. P. Chebyshev and Fourier Spectral Methods. Dover, New York, USA, 2001.
-
Fung T. C. Stability and accuracy of differential quadrature method in solving dynamic problems. Computer Methods in Applied Mechanical Engineering, Vol. 19, 2002, p. 1311-1331.
-
Berrut J. P., Trefethen L. N. Barycentric Lagrange interpolation. SIAM Review, Vol. 46, 2004, p. 501-517.
-
Belforte G., Gay P., Monegato G. Some new properties of Chebyshev polynomials. Journal of Computational and Applied Mathematics, Vol. 117, 2000, p. 175-181.
-
Fornberg B. A Pratical Guide to Pseudospectral Methods. Cambridge University Press, Cambridge, U.K, 1996.
-
Trefethen L. N. Spectral Methods in MATLAB. 1st Ed., SIAM, Philadelphia, USA, 2000.
-
Fox L., Parker I. P. Chebyshev Polynomials in Numerical Analysis. Oxford University Press, 1968.
-
Mai Duy N. An effective spectral collocation method for the direct solution of high-order ODEs. Communication in Numerical Methods in Engineering, Vol. 22, 2006, p. 627-642.
-
Babolian E., Hosseini M. M. A modified spectral method for numerical solution of ordinary differential equation with non-analytical solution. Applied Mathematics and Computation, Vol. 132, 2002, p. 341-351.
-
Weideman J. A. C., Reddy S. C. A MATLAB differentiation matrix suite. Transactions on Mathematical Software, Vol. 26, 2000, p. 465-519.
-
Maalawi K. Y. Functionally graded bars with enhanced dynamic performance. Journal of Mechanics of Materials and Structures, Vol. 6, Issues 1-4, 2011, p. 377-393.
