Abstract
Due to the friction and manufacturing and assembly errors, the clearance of revolution joints is unavoidable. When the clearance value increases to a certain value, the influence of clearance on the performance of the equipment could not be ignored. In this paper, the contact collision model is used to describe the effect of clearance. The model of reciprocating compressor is simplified properly, and the influence of revolution joint clearance on the system is studied by contact impact function. The influence of parameters on the acceleration of piston is studied by changing the size, position of clearance and velocity of crankshaft. The Lyapunov exponent of crosshead acceleration under the condition of load and no load are compared, which lays the foundation for studying the vibration of reciprocating compressor caused by clearance.
1. Introduction
The structure of reciprocating compressor is complex, and the excitation source is numerous, rotation of the drive motor and the crankshaft and other parts not only exist in the process of operation, there are also the reciprocating motion of the crosshead, piston and valves. The components are excited and coupled mutually with the change of reciprocating machine, which is the overall strong nonlinearity. Therefore, using conventional linear system analysis method, it is hard to get accurate results, which sometimes cannot explain some component fault phenomenon, thus increasing the difficulty of fault diagnosis and analysis.
In recent years, many scholars have studied the fault diagnosis of reciprocating compressor, mainly focused on the valve. Because the valve is installed on the outside of the reciprocating compressor, it is convenient to detect and install the valve. Kurt Pichler, et al. [1] investigated fault detection in reciprocating compressor valves under varying load conditions and Pichler K., Lughofer E., Pichler M., et al. [2] detected cracks in reciprocating compressor valves using pattern recognition in the pV diagram. Reciprocating compressor movement mechanism is mainly slider crank mechanism, for Paulo Flores and his team did a lot of research in the mechanism with joint clearance [3-5], which the multi clearance, the clearance of the moving pair and the contact impact detection are considered respectively. Haiyang Zhao, et al. [6] present a parameters optimization method for planar joint clearance model for dynamics simulation of reciprocating compressor and a multi-body dynamic model built in ADAMS software was used to solve this equation.
In this work, the dynamic simulation of reciprocating compressor with hinged clearance in ADAMS is introduced. The influence of clearance, velocity and piston force on the system is analyzed. The Lyapunov exponent is used to discuss whether the system is in chaos or not.
2. Revolute joint model with clearance
2.1. The relationship between journal and bearing position
Ideally, the center of the bearing in the revolute pair is coincident with the center of the journal. Due to the existence of the clearance between the moving pairs, the center position of the bearing and the shaft changes with the motion. Two generalized coordinates are added to the contact collision model and Lagrange equation, and manual calculation is more complicated.
Bearing clearance revolute axis and there are three different motion patterns [6]:
1) The freedom movement model, shaft bearings on contour free movement without bearing contact;
2) The collision mode occurs at the beginning and the end of the free motion mode, that is, the stage when the collision force is generated or disappeared;
3) Continuous contact mode, continuous contact between shaft and bearing; the penetration depth of shaft and bearing in contact process changes continuously along the periphery of shaft.
2.2. Contact force model
Simulation of clearance revolute contact process using the contact function of ADAMS software, the ideal operation analysis of crankshaft and connecting rod between the rotation of the crankshaft and connecting rod in the side to delete, add up to the contact function, through the contact force to drive the connecting rod to move, so close and the actual condition. The contact force is usually obtained by simulation of nonlinear spring damper. In the simulation process, the collision function starts with the contact between the shaft and the bearing, and can continuously calculate a series of responses of the contact parts and contact points.
The calculated normal contact force by the elastic and damping force is composed of two parts, which stretch is a function of the penetration depth, and the damping force is a function of the penetration rate.
Formula of normal contact force in model:
The local deformation of the contact region is defined as the penetration depth (: mm). The motion mechanism of reciprocating compressor for metal materials, elastic index 1.5.
The instantaneous damping coefficient and penetration depth relationship in ADAMS:
where, is the penetration depth corresponding to the maximum damping coefficient , which is generally set to 0.01 mm. Normally, the maximum damping factor is set to 1 % of the stiffness [7].
3. Simulation results and analysis of reciprocating compressor
Using the Solidworks software to build geometric model of reciprocating compressor and it is imported into ADAMS /View in Parasolid format. In ADMAS, piston, piston rod and crosshead fixed together, all reciprocating compressor parts are regarded as rigid body. The influence of the cylinder component on the dynamic performance of the transmission mechanism is equivalent to the effect of the piston load on the system, and the piston load is loaded on the piston with the step function. It is assumed that the wear occurs at the big end of the connecting rod, and the crankshaft is not worn. The inner diameter (original value: 180 mm) of big head tile of the connecting rod after wearing is 180.2 mm, 180.4 mm, 180.6 mm, respectively. Other reciprocating compressor parameters are shown in Table 1 [6] and gas forces acted on piston of each cylinder see Fig. 5. After the system is stable, the value of two cycles is plotted into Fig. 1-Fig. 4.
3.1. Influence of the clearance
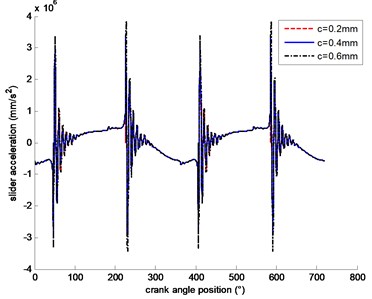
Fig. 1 and 2 show the relationship between the crank angle and the crosshead acceleration when the crank speed is 600 r/min and the clearance is 0.2 mm, 0.4 mm, and 0.6 mm respectively. When the clearance is different, acceleration of crosshead acceleration without load can be seen in Fig. 1. And acceleration of crosshead acceleration with load can be seen in Fig. 2. It is clear that the greater the clearance, the greater the impact on the crosshead acceleration.
Fig. 1Acceleration of crosshead without load
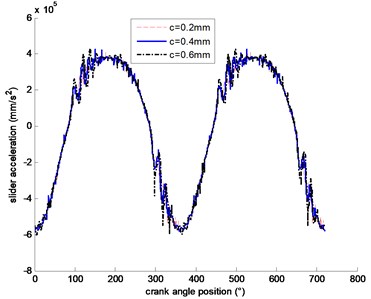
Fig. 2Acceleration of crosshead with load
3.2. Influence of the crank speed
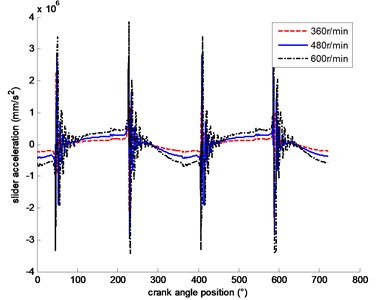
Figs. 3 and 4 show the relationship between the crank angle and the crosshead acceleration when the clearance is 0.6 mm and the crank speeds are 360 r/min, 480 r/min and 600 r/min respectively. When the crank speed is different, acceleration of crosshead without load can be seen in Fig. 3. And acceleration of crosshead with load can be seen in Fig. 4. With the crank speed increasing, whether or not there is a piston load, it can be seen from the two figures that the clearance has a greater influence on the crosshead acceleration.
Fig. 3Acceleration of crosshead without load
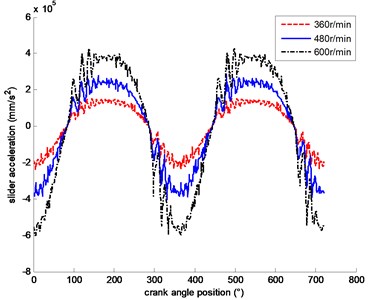
Fig. 4Acceleration of crosshead with load
4. Nonlinear analysis
Lyapunov exponent is one of the most effective methods to judge whether the system is chaotic or not. In this paper, the maximum Lyapunov exponent is used to judge whether the system is chaotic, and the wolf method is used to calculate the Lyapunov exponent.
When the crank speed is 600 r/min and the gap 0.2 mm, 0.4 mm, 0.6 mm, the corresponding Lyapunov exponents are 0.0053, 0.0027, 0.0042, and the corresponding Lyapunov exponent spectra are graphs Fig. 5(a), (b), (c). At the same time, the piston force is zero.
Fig. 5Lyapunov exponent spectra without load
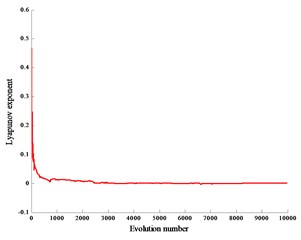
a)
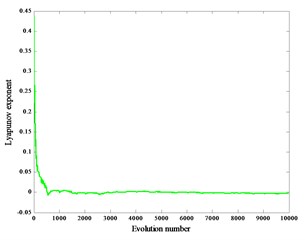
b)
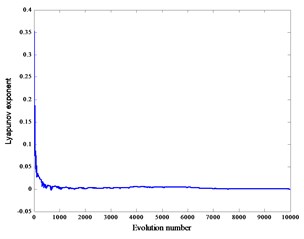
c)
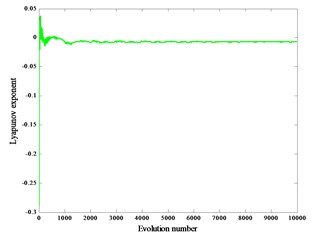
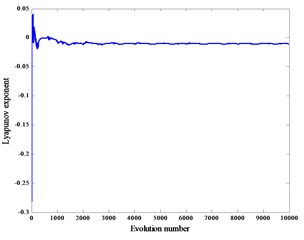
Fig. 6Lyapunov exponent spectra with load
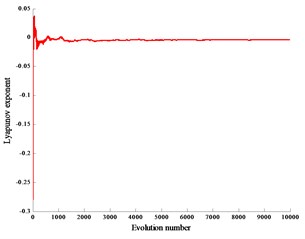
a)
b)
c)
When the reciprocating compressor works normally, the crank speed is 600 r/min and the gap 0.2 mm, 0.4 mm, 0.6 mm, the corresponding Lyapunov exponents are –0.0041, –0.0065, –0.0092, and the corresponding Lyapunov exponent spectra are graphs Fig. 6(a), (b), (c).
It is calculated that the Lyapunov exponent compares the piston with load when the clearance is 0.06 mm and the speed is 360 r/min, 480 r/min and 600 r/min respectively, and the calculation results are listed in the Table 1 of two cases. It can be seen that the system exhibits chaos in the case of no load. Under the action of piston force, the system is not chaotic.
Table 1Lyapunov exponent value of different crank speed
360 | 480 | 600 | |
No load | 0.0094 | 0.0050 | 0.0042 |
Load | –0.0149 | –0.0082 | –0.0092 |
5. Conclusions
In this work, the piston force of reciprocating compressor in different clearance and crank speed is modeled and calculated respectively. And the maximum Lyapunov exponent is used to judge whether the system is chaotic or not. The acceleration of the crosshead is affected by the piston force, and the bearing and the journal are always in contact, which changes the motion state. In simulation calculation, the crank speed is assumed to rotate at constant speed. The friction and lubrication effects are not considered. The contact impact model is provided by the ADAMS software. The equivalent piston force used simplifies the actual piston force and further studies will take more actual parameters into account in the simulation of reciprocating compressor.
References
-
Kurt Pichler, Edwin Lughofer, Markus Pichler, et al. Fault detection in reciprocating compressor valves under varying load conditions. Mechanical Systems and Signal Processing, Vols. 70-71, 2016, p. 104-119.
-
Pichler K., Lughofer E., Pichler M., et al. Detecting cracks in reciprocating compressor valves using pattern recognition in the pV diagram. Pattern Analysis and Applications, Vol. 18, Issue 2, 2015, p. 461-472.
-
Paulo Flores A parametric study on the dynamic response of planar multibody systems with multiple clearance joints. Nonlinear Dynamics, Vol. 61, 2010, p. 633-653.
-
Paulo Flores Remco Leine, Christoph Glocker, Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody System Dynamics, Vol. 23, 2010, p. 165-190.
-
Paulo Flores, Jorge Ambrósio On the contact detection for contact-impact analysis in multibody systems. Multibody System Dynamics, Vol. 24, 2010, p. 103-122.
-
Haiyang Zhao, Minqiang Xu A parameters optimization method for planar joint clearance model and its application for dynamics simulation of reciprocating compressor. Journal of Sound and Vibration, Vol. 344, 2015, p. 416-433.
-
Imed Khemili, Lotfi Romdhane Dynamic analysis of a flexible slide-crank mechanism with clearance. European Journal of Mechanics – A/Solids, Vol. 27, 2008, p. 882-898.
About this article
This work is supported by the Natural Science Foundation of China (51575331). We also wish to thank the anonymous reviewers and the editor for their helpful comments and suggestions.
