Abstract
Vibration is a major issue in rotor systems. Due to the presence of material property dispersions, manufacture or assembling errors and time-varying working status, rotor systems are always subject to uncertainties. The uncertainties should be taken into consideration to understand the dynamic characteristics of rotors more thoroughly. In this study, interval analysis is carried out to investigate the non-probabilistic characteristics of a double-disk rotor with uncertain parameters. The uncertainties are modeled as uncertain-but-bounded variables due to insufficient essential information to define their precise probabilistic distributions. The deterministic analysis model is derived by the finite element method (FEM). The accuracy and effectiveness of the proposed method in solving uncertain rotor problems are validated by comparative study with the Monte Carlo simulation (MCS). Several cases where different physical parameters are regarded as uncertain are investigated and the dynamic response bounds are obtained. Simulations suggest that uncertainties have significant influence on the dynamic characteristics of the rotor system. Multi-source uncertainties propagation can cause heavy vibrations in mechanical systems.
1. Introduction
Rotor system is a crucial part of rotating machinery such as aero-engines and electric generators. One of the fundamental and significant issues encountered in rotor systems is the heavy vibration aroused by the mass unbalance. The dynamic characteristics are frequently investigated by designers and researchers to understand the performance of a rotor system. Many efforts have been put in during the past few decades both theoretically and experimentally [1-8]. As can be seen, these contributions were mostly focused on rotor systems in which the parameters and loads are all deterministic. The fact is that uncertainty is unavoidable in practice, which is especially true in rotor systems. Material property dispersions, varying working status and assembly or measurement errors are all possible sources of uncertainty. In uncertain problems, the traditional analysis methods fail to give reasonable estimations of the response ranges induced by uncertain inputs. Thus, new solution methods should be incorporated.
Pioneering works have been done to study rotordynamics involved with various kinds of uncertainties [9]. Liao [10] proposed a global resonance optimization method and applied it to the uncertainty quantification of rotor systems. Didder and Sinou et al. [11, 12] had carried out many researches concerning uncertain rotor systems with nonlinearity and faults in which the uncertainties were represented by the Polynomial Chaos Expansion (PCE). The PCE was also applied to analyze the performance of a H-Darrieus rotor under uncertainty in transient turbulent flow simulations recently [13]. Sinou et al. [14] further studied the effect of the PCE order on the dynamic response of an asymmetric uncertain rotor using a recursive stochastic harmonic balance method. Gan et al. [15] studied the sensitivity of the first order critical speed of an uncertain Jeffcott rotor to uncertain parameters via the MCS. It was found that the uncertain effect cannot be neglected in some circumstances. The proper orthogonal decomposition method can be applied to model reduction for deterministic and random rotor systems [16]. Li et al. [17] investigated the nonlinear stochastic response of an angular misalignment rotor considering the fluid induced random forces. Nonparametric stochastic modelling method for uncertain rotor systems in unbalance and balancing aspects was proposed by Murthy et al. [18]. It should be noted that all the works above were done in the probabilistic frame, which means that the precise distributions of the uncertainties must be known beforehand. That is a requirement hard to meet due to lack of sufficient statistical information. For example, the epistemic uncertainty introduced by the designer’s inadequate essential knowledge is generally difficult to define. In that case, the probabilistic methods are sometimes inapplicable. However, the varying ranges of uncertain parameters are usually easy to obtain, which can be described by uncertain-but-bounded variables. So non-probabilistic based methods are advocated in general uncertain problems and the interval analysis method is a typical one among them. A universal review of the non-probabilistic methods for the FEM analysis in uncertain problems was contributed by Moens et al. [19]. Qiu et al. [20] had proposed many interval approaches including perturbation method, Taylor interval expansion method and interval collocation method to calculate static and dynamic problems in structures. Qi et al. [21] further compared these interval methods with probabilistic ones in the aspects of efficiency, accuracy and overestimations. Wu et al. [22] proposed a non-intrusive interval method for dynamic systems with uncertain parameters by introducing the Chebyshev inclusion function, which has been successfully applied to uncertain vehicle systems [23]. It can achieve high efficiency and accuracy with low expansion order and control the overestimation effectively. So far, few researches can be found using interval methods for uncertain rotor problems. Ma et al. [24-27] studied the variations of the critical speeds, dynamic responses and modes in uncertain rotor systems using combination of perturbation method, the interval modal superposition method and interval Taylor expansion method. Fang et al. [28] applied the interval method to a simple rotor model for modal characteristic investigations. These methods were validated by different rotor systems with considerable accuracy. However, an important feature of them is that modifications need to be made to the original procedure. In other words, they are intrusive.
In this study, the non-probabilistic dynamic response analysis of a double-disk rotor with uncertain-but-bounded parameters is carried out based on interval analysis in a non-intrusive way. The FEM is used to derive the deterministic analysis model. In order to verify the accuracy and efficiency of the interval method in solving uncertain rotordynamics, the results are compared with those obtained by the MCS. Several simulations are done considering different uncertain parameters. Some conclusions are drawn based on the simulation results.
2. Rotor model and equations of motion
In this paper, a double-disk rotor system supported by two journal bearings is considered. The two disks are located in the middle of the elastic shaft and the layout of the system is shown in Fig. 1(a). The FEM is used to discretize the system into elements with two nodes each. The nodal displacement vector, which consists of two rotating angles and two lateral displacements, is defined by in fixed coordinates as demonstrated in Fig. 1(b) [11]. The deterministic values of physical parameters of the rotor are given in Table 1.
The equations of motion of the rotor system can be obtained by assembling all of the shaft elements:
where , , and are the global mass, damping, gyroscopic and stiffness matrices of the system, respectively. , and represent the displacement, velocity and acceleration vectors, respectively. is the excitation vector and corresponds to the rotating speed.
Table 1Parameter values of the rotor system
Parameter description | Value | Parameter description | Value |
Length 1, | 0.05 m | Young’s modulus, | 2.1×1011 N⋅m-2 |
Length 2, | 0.16 m | Support stiffness 1, | 7×105 N⋅m-1 |
Length 3, | 0.2 m | Support stiffness 2, | 5.5×105 N⋅m-1 |
Length 4, | 0.18 m | Density, | 7800 kg⋅m-3 |
Length 5, | 0.01 m | Viscous damping 1, | 50 N⋅s⋅m-1 |
Shaft diameter, | 0.03 m | Viscous damping 2, | 50 N⋅s⋅m-1 |
Mass of disk 1, | 1.5 kg | Eccentricity on disk 1, | 1×10-4 m |
Mass of disk 2, | 4 kg | Eccentricity on disk 2, | 5×10-5 m |
Diameter of disk 1, | 0.09 m | Diameter of disk 2, | 0.15 m |
Fig. 1Double-disk rotor schematic diagram: a) rotor system and b) coordinates in fixed frame
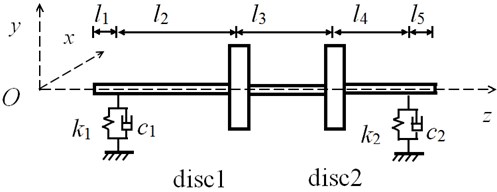
a) Rotor system
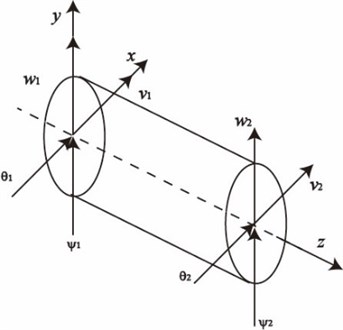
b) Coordinates in fixed frame
3. Interval analysis of the uncertain rotor response
The interval analysis methods are widely used nowadays in uncertain dynamic investigations. Approximation theory and derivative information are all introduced into the calculation process [21, 22]. These kind of interval procedures are non-intrusive and capable of controlling the large overestimation compared with Taylor series based methods. High accuracy can be achieved via low expansion orders and a few interpolations. Moreover, it is convenient to obtain higher accuracy by higher order and more interpolation points while the computation effort is not increased enormously comparing with the MCS.
Firstly, we define an interval variable in mathematic form:
in which superscript denotes an interval character, and are the lower and upper bounds of the uncertain variable . The first class Chebyshev orthogonal polynomials can be described as:
where is a nonnegative integer. The one-dimensional Chebyshev approximation is defined as:
where are the expansion coefficients. They can be expressed as:
in which is the function being approximated and is the deterministic value of . is the weight function. The integration can be further calculated by the Gauss-Chebyshev integration formulas:
with being the number of interpolation points. In order to use the boundedness of trigonometric functions, the variable can be replaced as:
where .
As stated previously, we consider that the rotor system under study subject to uncertainties and then the parameters such as the support stiffness and density are all uncertain [24]. No sufficient data is available to define their probabilistic distributions. Therefore, the uncertainties are modeled as uncertain-but-bounded parameters. For clarity, we define an uncertain parameter vector, which is composed of all the uncertain parameters in the rotor system:
in which is the total number of uncertain parameters. The th member of can be expressed in interval form as:
where and are the lower and upper bounds, respectively. is the mean value of the parameter and represents the deviation coefficient. The matrices in the general equations of motion are all related to one or more members of the uncertain parameter vector, thus Eq. (1) can be rewritten as:
The dynamic response calculation of the system can be interpreted as initial value problems of Eq. (10) under the constraints of Eq. (8) with respect to time :
in which is the initial value of the response displacement vector, represents the possible interval parameter vector comprised of individuals expressed by Eq. (9). The multi-dimensional Chebyshev orthogonal approximation of Eq. (11) is:
where is the number of zeros in subscripts, is the expansion order. represents the -dimensional Chebyshev orthogonal series which is defined as [22]:
denotes the -dimensional expansion coefficient, which can be obtained by Mehler integration at Chebyshev interpolation points. The expression is:
with representing the Chebyshev interpolation point, being the total interpolation point number which should be no less than for the benefit of accuracy. denotes the deterministic rotor response values calculated at interpolation points. They can be numerically solved by regular numerical integration method as deterministic ODEs. Generally, the interpolation points are the zeros of the Chebyshev series:
The response interval of the double-disk rotor system is finally given by:
Now, we have transformed the uncertain dynamic problem into a set of deterministic problems at the interpolation points and the structures of the governing motion equations remain unchanged compared with Eq. (1). The dynamic response range can then be explicitly calculated by interval arithmetic as denoted by Eq. (16).
4. Numerical results and discussions
The non-probabilistic dynamic response of the uncertain rotor system detailed in Section 2 is obtained based on interval arithmetic and the Newmark- numerical integration method which has been proved to be unconditionally stable as long as the integral parameters are chosen properly [29]. To verify the effectiveness and accuracy of the interval method, results are compared with those calculated by the MCS [30]. Then the uncertain responses in single or multi-dimensional uncertainties are investigated, respectively.
4.1. Deterministic dynamic response
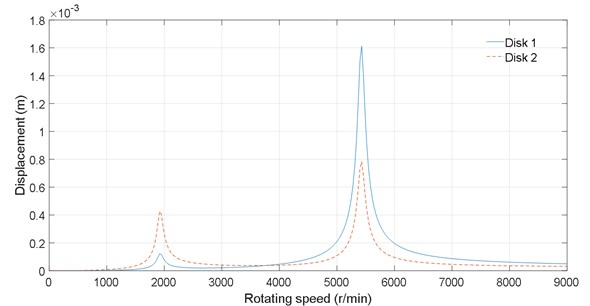
Based on the deterministic parameters of the rotor model, the dynamic characteristic analysis of the double-disk rotor system is carried out. Fig. 2 illustrates the steady state responses of the rotor for deterministic parameters in a traditional sense. The first two critical speeds are 1920 revolutions per minute (r/min) and 5435 r/min. The resonant peaks of the two disks are given by Table 2. It can be observed from Fig. 2 that the vibration of the second resonance is higher than the first one which is especially true for disk 1. In all of the uncertain dynamic response figures presented in the following text, the deterministic steady state response will be plotted firstly for direct reference.
Table 2Deterministic dynamic characteristics of the rotor
1st resonant peak (at 1920 r/min) | 2nd resonant peak (at 5435 r/min) | |
Disk 1 | 1.23×10-4 m | 1.61×10-3 m |
Disk 2 | 4.28×10-4 m | 7.85×10-4 m |
Fig. 2The steady state response of the deterministic rotor model
4.2. Method verification
In this subsection, we use the MCS to verify the accuracy and efficiency of the interval method in solving non-probabilistic uncertain dynamic problems. For simplicity and clarity, the dynamic response ranges under one-dimensional uncertainty at several rotating speeds are investigated. The support stiffness 1 is assumed to be uncertain which can be expressed in interval form as:
where and are the mean value and the deviation coefficient of . The response bounds under deviation coefficient 10 % obtained from the MCS and the interval method are given in Table 3. Total sampling times in the MCS are 100 and 500. The results calculated with different expansion order and interpolation points are also given in the table for comparisons. We refer the interested readers to Ref. [21] for the selection principles of the calculation parameters based on the truncation error of the Chebyshev approximation. To illustrate the computational efforts taken in the two approaches, the computing costs (CPU time) are listed in Table 4. In Tables 3 and 4, RS is short for rotating speed and IA is the abbreviation of interval analysis.
From Table 3, it is observed that the response ranges calculated by the interval method are in good agreement with those generated by the MCS, which is considered to be accurate on the premise of sufficient samples. The response bounds calculated from the interval method with different expansion orders and interpolation numbers are almost identical when two decimal digits are kept. It can be concluded that the results are accurate adequately when the expansion order is 5 and the interpolation number is 10. There is still some discrepancy between the ranges obtained from the interval method and the MCS, which is small and acceptable. It can be explained that the sampling times is finite and minor errors could be introduced by the interval arithmetic. As demonstrated in Table 4, the computing time for the MCS to obtain accurate results is much longer than the interval method which indicates the efficiency of the latter. Moreover, increasing the expansion order introduces little computation cost. The results validate the accuracy and effectiveness of the interval method. Hereafter, we used the expansion order 5 and 10 interpolation points in the interval analysis.
Table 3Displacement bounds of disk 1 obtained from the MCS and the interval method (μm)
RS (r/min) | MCS (100 samples) | MCS (500 samples) | IA ( 5, 10) | IA ( 7, 10) | IA ( 5, 12) |
1800 | [41.01,42.28] | [40.98,42.28] | [40.97,42.28] | [40.97,42.28] | [40.97,42.28] |
4200 | [50.32,69.87] | [50.23,70.83] | [50.23,70.83] | [50.23,70.83] | [50.23,70.83] |
5100 | [175.76,684.97] | [175.76,714.26] | [175.66,716.65] | [175.69,716.41] | [175.67,716.58] |
5700 | [220.38,929.42] | [220.40,1007.3] | [220.17,1014.3] | [220.20,1014.3] | [220.18,1014.3] |
6000 | [147.44,288.38] | [146.04,290.17] | [146.04,290.17] | [146.04,290.17] | [146.04,290.17] |
Table 4The average cost of computing time (s)
MCS (100 samples) | MCS (500 samples) | IA ( 5, 10) | IA ( 7, 10) | IA ( 5, 12) | |
Time elapsed | 122.65 | 628.82 | 18.23 | 19.01 | 21.19 |
4.3. Non-probabilistic analysis under different uncertainties
In this part, some parameters are regarded as uncertain-but-bounded variables and the corresponding dynamic responses are analyzed. The deviation coefficient is set to 10 % and the displacement of disk 1 with respect to rotating speed is presented in the single dimensional cases. For the multi-dimensional case, the response ranges of disk 1 and disk 2 are investigated. It should be noted that any location of interest in the rotor system with different deviation coefficients can be analyzed via the solution procedure if necessary.
4.3.1. Uncertain support stiffness
The effects of the uncertain stiffness of support 1 are investigated in this subsection which is expressed as Eq. (17). The dynamic response bound curves under 10 % deviation coefficient are plotted in Fig. 3. As we can see from Fig. 3, the response deviates from the original deterministic one in the presence of uncertainty and the deviation is especially obvious in the resonant areas. However, the deviation is not symmetric about the deterministic curve with a larger offset in the upper bound before and after the resonant peak while near the peak point the lower bound deviates further. It can be explained that the solution algorithm searches the maximum and minimum response in the uncertain parameter interval and the deterministic resonant peak is given in the near vicinity of the critical speed while the furthest and also lowest response is set as the lower bound. The resonant peak is shifted due to inherent stiffness matrix changes which influence the critical speeds of the system directly. The response of this rotor is sensitive to the stiffness of support 1 and a resonance band appears near the second critical speed where the displacement is large. It implies that the resonant region is expanded, and the displacement may stay high in a relatively wide rotating speed range around the critical speeds. Local fluctuations of the response upper curve in the resonant region are observed which could be caused by the errors introduced in the interval algorithm and it may be influenced by the expansion orders.
4.3.2. Uncertain density
To account for the uncertainty introduced by material dispersion, the density of the system is considered to be uncertain and treated as interval variable as:
where and are the nominal value and the deviation coefficient of the density, respectively.
The response varying range under 10 % uncertainty of the density is plotted in Fig. 4. It can be noted that the dynamic response is also sensitive to the density and a large displacement area is observed. The resonant peak is shifted as illustrated in Fig. 4. Also, we can see that there are local fluctuations in the top band of the second critical speed which assure again the high sensitivity of the dynamic response to the uncertain parameter.
Fig. 3Dynamic response under the stiffness uncertainty
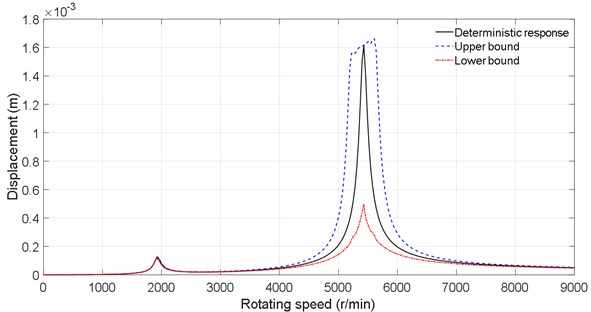
Fig. 4Dynamic response under the density uncertainty
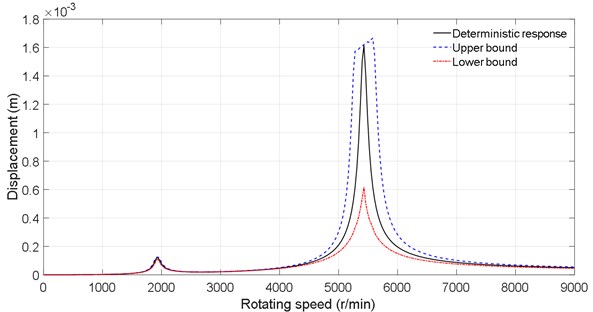
4.3.3. Effect of multi-source uncertainties
In this subsection, the effects of multi-dimensional uncertainties on the uncertain dynamic characteristics are analyzed. Considering multi-source of uncertainties, the stiffness of support 1 and the density are assumed to be uncertain-but-bounded parameters. The non-probabilistic response ranges are obtained using the interval analysis procedure under a typical uncertain deviation coefficient 10 %. Figs. 5 and 6 are the response bounds of disk 1 and disk 2. Multi-source uncertainties can result in unexpected high displacement vibration in a large rotating speed range. The local fluctuations are more obvious compared with former cases. The resonant peaks of the upper bounds are shifted to the right and the lower ones to the left due to the changes in critical speeds caused by multiple uncertainties.
Fig. 5Dynamic response of the disk 1 under multiple uncertainties
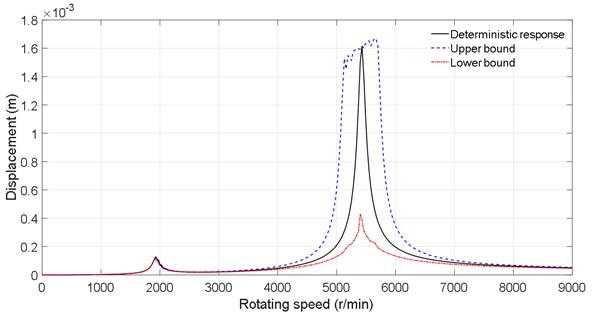
Fig. 6Dynamic response of the disk 2 under multiple uncertainties
5. Conclusions
This work aims at analyzing the dynamic characteristics of a double-disk rotor system with non-probabilistic uncertain parameters included. The interval method is applicable when the precise probabilistic distribution is unknown and insufficient prior information to implement stochastic methods. Two parameters in this paper are modeled as uncertain-but-bounded variables and the corresponding dynamic response ranges are investigated. The MCS is utilized to illustrate the accuracy and effectiveness of the interval method. From the results, it is clear that the interval method is efficient in solving uncertain rotor dynamics and satisfactory accuracy can be achieved via low expansion orders and a few interpolation points. Based on the simulations in the previous sections, several conclusions can be summarized as follows:
1) The uncertainties in rotor systems have significant effects on the dynamic response which evolved from deterministic value to a response range. The influence of uncertainties is notable in the resonant regions while weak in other areas. The interval method can also be used to analyze the sensitivities of the dynamic response to system parameters.
2) A high displacement band appears in several uncertain cases. The displacement is high in a rotating speed range close to the critical speeds in comparison with the original one.
3) In some cases, there are obvious shifts of the resonant peaks due to the variations of the critical speeds.
4) Multiple source uncertainties can cause large offset of the dynamic response and small range uncertainties propagation has major impacts on the dynamic characteristics of the rotor systems. To understand the uncertain dynamic characteristics more thoroughly, it is advised that the uncertainties be taken into consideration in the design or maintenance of rotors.
References
-
Saxena A., Chouksey M., Parey A. Effect of mesh stiffness of healthy and cracked gear tooth on modal and frequency response characteristics of geared rotor system. Mechanism and Machine Theory, Vol. 107, 2017, p. 261-273.
-
Ma H., Shi C., Han Q., Wen B. Fixed-point rubbing fault characteristic analysis of a rotor system based on contact theory. Mechanical Systems and Signal Processing, Vol. 38, Issue 1, 2013, p. 137-153.
-
Li H., Meng G., Meng Z., Wen B. Effects of boundary conditions on a self-excited vibration system with clearance. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 8, Issue 4, 2007, p. 571-580.
-
Yang Y., Chen H., Jiang T. Nonlinear response prediction of cracked rotor based on EMD. Journal of the Franklin Institute, Vol. 352, Issue 8, 2015, p. 3378-3393.
-
Hou L., Chen Y., Cao Q. Nonlinear vibration phenomenon of an aircraft rub-impact rotor system due to hovering flight. Communications in Nonlinear Science and Numerical Simulation, Vol. 19, Issue 1, 2014, p. 286-297.
-
Chu F., Lu W. Experimental observation of nonlinear vibrations in a rub-impact rotor system. Journal of Sound and Vibration, Vol. 283, Issue 5, 2005, p. 621-643.
-
Li C., She H., Tang Q., Wen B. The effect of blade vibration on the nonlinear characteristics of rotor-bearing system supported by nonlinear suspension. Nonlinear Dynamics, Vol. 89, Issue 2, 2017, p. 987-1010.
-
Qin Z., Han Q., Chu F. Analytical model of bolted disk-drum joints and its application to dynamic analysis of jointed rotor. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science, Vol. 228, Issue 4, 2014, p. 646-663.
-
Yang L., Zhang J., Guo Y. Uncertainty representation and quantification for a nonlinear rotor/stator system with mixed uncertainties. Journal of Vibroengineering, Vol. 18, Issue 7, 2016, p. 4836-4851.
-
Liao H. Global resonance optimization analysis of nonlinear mechanical systems: application to the uncertainty quantification problems in rotor dynamics. Communications in Nonlinear Science and Numerical Simulation, Vol. 19, Issue 9, 2014, p. 3323-3345.
-
Sinou J. J., Didier J., Faverjon B. Stochastic non-linear response of a flexible rotor with local non-linearities. International Journal of Non-Linear Mechanics, Vol. 74, 2015, p. 92-99.
-
Didier J., Sinou J. J., Faverjon B. Study of the non-linear dynamic response of a rotor system with faults and uncertainties. Journal of Sound and Vibration, Vol. 331, Issue 3, 2012, p. 671-703.
-
Daróczy L., Janiga G., Thévenin D. Analysis of the performance of a H-Darrieus rotor under uncertainty using Polynomial Chaos Expansion. Energy, Vol. 113, 2016, p. 399-412.
-
Sinou J. J., Jacquelin E. Influence of Polynomial Chaos expansion order on an uncertain asymmetric rotor system response. Mechanical Systems and Signal Processing, Vol. 50, Issue 51, 2015, p. 718-731.
-
Gan C., Wang Y., Yang S., Cao Y. Nonparametric modeling and vibration analysis of uncertain Jeffcott rotor with disc offset. International Journal of Mechanical Sciences, Vol. 78, 2014, p. 126-134.
-
Lu K., Chen Y., Jin Y., Hou L. Application of the transient proper orthogonal decomposition method for order reduction of rotor systems with faults. Nonlinear Dynamics, Vol. 86, Issue 3, 2016, p. 1913-1926.
-
Li Z., Jiang J., Tian Z. Stochastic dynamics of a nonlinear misaligned rotor system subject to random fluid-induced forces. Journal of Computational and Nonlinear Dynamics, Vol. 12, Issue 1, 2017, p. 11004.
-
Murthy R., Tomei J. C., Wang X. Q., Mignolet M. P., El-Shafei A. Nonparametric stochastic modeling of structural uncertainty in rotordynamics: unbalance and balancing aspects. Journal of Engineering for Gas Turbines and Power, Vol. 136, Issue 6, 2014, p. 62506.
-
Moens D., Hanss M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: recent advances. Finite Elements in Analysis and Design, Vol. 47, Issue 1, 2011, p. 4-16.
-
Qiu Z., Ma L., Wang X. Non-probabilistic interval analysis method for dynamic response analysis of nonlinear systems with uncertainty. Journal of Sound and Vibration, Vol. 319, Issues 1-2, 2009, p. 531-540.
-
Qi W., Qiu Z. A collocation interval analysis method for interval structural parameters and stochastic excitation. Science China Physics, Mechanics and Astronomy, Vol. 55, Issue 1, 2012, p. 66-77.
-
Wu J., Zhang Y., Chen L., Luo Z. A Chebyshev interval method for nonlinear dynamic systems under uncertainty. Applied Mathematical Modelling, Vol. 37, Issue 6, 2013, p. 4578-4591.
-
Wu J., Luo Z., Zhang N., Zhang Y. A new uncertain analysis method and its application in vehicle dynamics. Mechanical Systems and Signal Processing, Vol. 50, Issue 51, 2015, p. 659-675.
-
Ma Y., Liang Z., Chen M., Hong J. Interval analysis of rotor dynamic response with uncertain parameters. Journal of Sound and Vibration, Vol. 332, Issue 16, 2013, p. 3869-3880.
-
Wang J., Hong J., Chen M., Ma Y. Non-probabilistic analysis on aero-engine rotordynamics. Journal of Aerospace Power, Vol. 27, 2012, p. 75-81, (in Chinese).
-
Hao Y., Chen M., Hong J., Ma Y. Interval analysis method of rotordynamics based on Taylor expansion method. Journal of Aerospace Power, Vol. 29, 2014, p. 571-577, (in Chinese).
-
Wang C., Ma Y., Zhang D., Hong J. Interval analysis on aero-engine rotor system with misalignment. Turbine Technical Conference and Exposition, ASME, Montréal, Canada, 2015.
-
Fang B., Zhang J., Gao Y. Interval analysis method for dynamical properties of rotor system with uncertain parameters. Journal of Shenyang University of Technology, Vol. 39, 2017, p. 84-87, (in Chinese).
-
Park K. Practical aspects of numerical time integration. Computers and Structures, Vol. 7, Issue 3, 1977, p. 343-353.
-
Dimarogonas A. D. Interval analysis of vibrating systems. Journal of Sound and Vibration, Vol. 183, Issue 4, 1995, p. 739-749.
About this article
This work was supported by National Natural Science Foundation of China (11272257), Aerospace Science and Technology Innovation Fund (2016KC060013) and the Fundamental Research Funds for the Central Universities (3102016ZY016).
