Abstract
This paper presents an analytical approach to investigate the free vibration analysis of cracked non-uniform beam carrying spring-mass systems by finite element method and illustrates a valid and reliable damage identification method which using hybrid neural genetic technique. Firstly, based on the finite element method, the dynamic characteristics of non-uniform cracked beam carrying spring-mass systems are obtained. Then, the first five frequencies are used as input parameters by combining genetic algorithm with neural network to identify the damage. Finally, Numerical simulations of direct and inverse problems of non-uniform cracked beams carrying a spring-mass system are carried out.
1. Introduction
Crack is one of the most common structural damage, and the existence of cracks will greatly affect the performance and the residual life of structures. The structure is often subjected to dynamic loads during the process of using. Therefore, the dynamic characteristics of cracked structures have attracted many particular attentions. On the other hand, the presence of cracks can lead to the changes of structural physical parameters, which causes the changes in its dynamic characteristics. So, it means that the damage identification based on the dynamic characteristics has great potential [1]. And the non-uniform beam carrying spring-mass systems is widely used in civil engineering, mechanical engineering and other fields. Therefore, it is of great significance to study direct and inverse problems on free vibration analysis of cracked non-uniform beams carrying spring-mass systems.
The research on the dynamic behavior of cracked beams has received a great deal of attention. And the various kinds of analytical, semi-analytical and numerical methods have been employed to solve the vibration analysis of cracked beam structures. The beam can be divided into several sub-beams by cracks simulated by massless rotational springs and then the general solution for eigenfunctions of every sub-beam contains four unknown constants, which leads to a system of 4() equations in the case of cracks [2]. Based on the transfer matrix method (TMM), Tan et al. [3] studied the natural frequencies and mode shapes of cracked Timoshenko beams carrying spring-mass systems. By using modified Fourier series (MFS), Zheng and Fan [4] obtained the natural frequencies of a non-uniform beam with an arbitrary number of transverse open cracks. The finite element method (FEM) is widely used for free vibration analysis of damaged beams [5] and the key problem in using FEM is how to appropriately obtain the stiffness matrix for the cracked beam element.
Structural damage identification has played an important role for ensuring safety, implementing rescues and avoiding emergency action. In the studies of the inverse problem, the genetic algorithms, artificial neural network, fractal dimension-based method and so on have been adopted to identify cracks in the structures. By using the genetic algorithms, Mehrjoo et al. [6] proposed a crack detection methodology for detecting cracks in beam-like structures. An artificial neural network based approach is presented by Jeyasehar and Sumangala [7] for the assessment of damage in prestressed concrete beams. This paper presents an analytical approach to study the free vibration of cracked non-uniform beam carrying spring-mass systems by finite element method and illustrates a damage identification method which based on hybrid neural genetic algorithm.
2. Theoretical background
2.1. Fundamental theory of free vibration analysis of the non-uniform cracked beam
The free vibration equation of the non-uniform intact beam using the finite element method is expressed by:
where, and are the mass matrix and stiffness matrix of the non-uniform beam, respectively. and are the acceleration and displacement vectors of the degrees of freedom of each node.
Let be the flexibility matrix of the non-uniform intact beam. According to the basic concepts of structural analysis, we know that:
Dimarogonas et al. [8] presented an attractive method for modeling open edge crack in a beam as a local flexibility which can be derived from the stress intensity factors based on the theory of fracture mechanics. Zheng and Kessissoglou [5] presented that the flexibility of the cracked beam can be obtained by putting the flexibility of the intact beam and the local flexibility due to crack together. Then the flexibility of cracked beam can be expressed as:
where, is the flexibility matrix of the cracked beam; is the local flexibility matrix caused by the crack.
The stiffness matrix of the cracked beam is expressed by . According to the relation between the structural flexibility matrix and stiffness matrix expressed in Eq. (2), one obtains . The existence of the crack does not lead to the change of the structural mass matrix, then the free vibration equation of the cracked beam can be written as:
Assume that the degrees of freedom of each node do harmonic vibration near the equilibrium position, it has:
where, is the vibrational amplitude vector corresponding to ; is the circular frequency of the cracked beam, .
Substituting Eq. (5) into Eq. (4), one obtains:
Eq. (6) can be written as:
It can be known from Eq. (7) that the eigenvalues of the matrix are the square of the natural frequencies of the cracked beam, and the characteristic vectors are the mode shapes of the cracked beam. By using the similar procedure, it could also be obtained that the square and mode shape of the natural frequency of the intact beam are the eigenvalue and eigenvector of the matrix . From the above analysis, one sees that the existences of cracks result in the changes in the structural stiffness matrix, which leads to the changes of the dynamic characteristics.
Under the action of spring-mass system, the vibration equation of the cracked beam is:
where, , is the position matrix of the force acting point; is the force of the spring-mass system acting on the beam.
According to the principle of mode superposition, it has:
where, , , is the th order mode shape of the cracked beam; is the modal coordinate corresponding to .
Substituting Eq. (9) into Eq. (8) and left multiply can obtain:
where, includes the acceleration and displacement of all degrees of freedom of beam nodes, and those of the spring mass system [9]. So, Eq. (10) can be expressed as:
where, , , ; and are the mass matrix and stiffness matrix of spring-mass system, respectively; is the coupling stiffness of the cracked beam and spring-mass system; is the modal coordinate vector of spring-mass system.
The analysis of Eq. (11) shows that the dynamic characteristics of cracked beam with spring-mass system are the characteristic value and characteristic vector for the matrix . The spring-mass system will not only lead to the variation in stiffness matrix of the vibration system, but also cause the changes in mass matrix. Therefore, it can be considered that the spring-mass system could result in the change of the dynamic characteristics of the beam or the cracked beam.
2.2. Theoretical basic of inverse problem for free vibration analysis of the cracked beam
In this paper, a damage identification method for cracked beams is proposed based on hybrid neural genetic technique. As a global optimization algorithm, genetic algorithm (GA) is a random search algorithm based on natural selection and natural genetic mechanism. By minimizing the error between the numerical simulation and the measured frequencies, the fitness of each individual in the swarm is estimated to achieve the wide-range search. The BP network is optimized by using the characteristic of global optimization of GA in this paper.
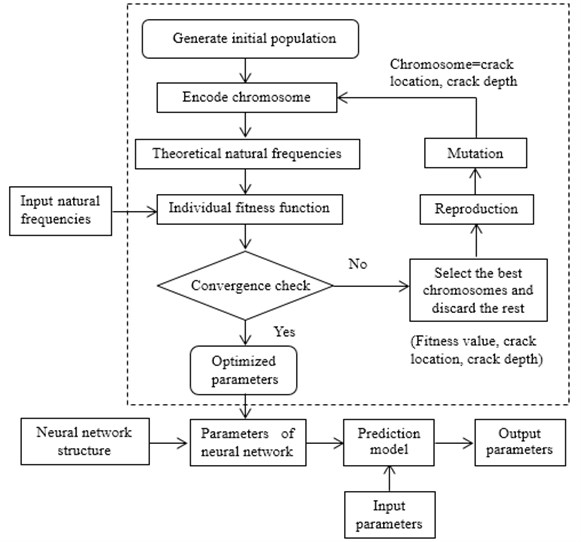
The three layer BP neural network is adopted in this paper. The input parameter is the first 5 natural frequencies of the cracked beam, and the output parameter is the location and depth of the crack. The “trainlm” function is used as the training function of the network and the pure linear transformation function is adopted in the output layer neuron. The Levenberg-Marquardt algorithm is chosen as the training algorithm of the network, and the corresponding learning rate and training target are set up. When the algorithm is used to identify the damage, firstly GA is employed to optimize the weights and thresholds of the network. Then the optimization results are adopted as the initial value of the three layer BP neural network. Through the training of sample data, the suitable network is established. Finally, using the natural frequencies as the test values to obtain the predicted results of crack parameters. The process of the hybrid genetic algorithm is shown in Fig. 1.
Fig. 1The process of the hybrid genetic algorithm
3. Numerical examples of direct problem
The non-uniform cracked fixed-free beam shown in Fig. 2 has one spring-mass system. The numerical results are obtained based on the beam with the following given data: rectangular cross section with uniform width of 0.3 m, the height of the beam varies linearly and the height 0.8 m, 0.4 m. Young’s modulus 3.25×1010Pa, mass density 2500 kg/m3, Poisson’s ratio 0.3. For the parameters of spring-mass system, the point mass is 1500 kg and the spring coefficient is60000 N/m. Two cases of the cracked beam are investigated by the proposed method.
Case1: only single crack occurs at 4m from the fixed end of the beam carrying one spring mass system, the relative depth () of the crack changes from 0 % to 30 % at intervals of 5 %.
Case2: the same crack position and relative depth (30 %) with Case 1 and the second crack occurs at 8 m from the fixed end of the beam which also changes from 0 % to 30 % at intervals of 5 %.
The change ratio for natural frequency is defined by Eq. (12) and the calculated results of the fixed-free beam are presented in Fig. 3:
where is the natural frequency of cracked beam with spring-mass systems, is the natural frequency of intact beam without spring-mass systems.
Fig. 2A cracked fixed-free beam with one spring-mass system
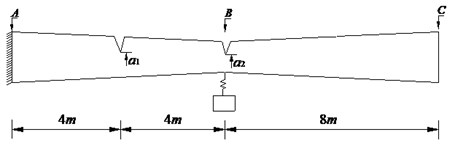
Fig. 3Change ratios for natural frequencies of fixed-free beam
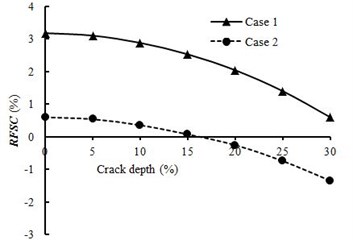
a) RFSC of the first order natural frequency
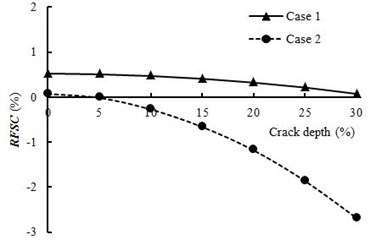
b) RFSC of the second order natural frequency
As can be seen from Fig. 3, when the relative crack depth is 0 %, the first two natural frequencies of fixed-free beam increase by the influence of spring-mass system, in which the change of the first natural frequency is more significant than that of the second one. This is because the spring-mass system is located at different points with respect to the lowest two mode shapes and the positive RFSC is attributed to the attached spring-mass system. Then the lowest two natural frequencies of fixed-free beam decrease with relative crack depth increasing, which indicates that crack has a negative influence on RFSC.
4. Numerical examples of inverse problem
The non-uniform cracked fixed-free beam carrying a spring-mass system (shown in Fig. 2) is used to simulate the crack diagnosis. There are 6 kinds of crack case, in which there are three cases for single crack and double cracks, respectively. The first five natural frequencies are adopted as input data in all cases of the crack diagnose. Furthermore, in order to investigate the anti-noise ability of the crack identification algorithm in this paper, different levels of noise is added into the first five natural frequencies calculated by the present method. The expression of the natural frequency with noise is written as:
is the randon generator function in MATLAB with a zero mean and a standard deviation of , is error lever. The noise level is controlled by the error lever and the inverse problem is solved under three different values of 3 %, 6 %, 9 %, respectively. The results of crack identification of the double I-section beam are presented in Tables 1-2.
According to the calculated results in Tables 1-2, crack parameters of cracked non-uniform fixed-free beam carrying a spring-mass system can be determined effectively and accurately by the presented method in this paper. It is also observed that the reliability of the present method is influenced by the level of noise pollution.
Table 1Crack identification of the fixed-free beam with single crack
Case | Error lever (%) | Crack location (m) | Crack depth () | ||||
Actual | Predicted | Error (%) | Actual | Predicted | Error (%) | ||
1 | 3% | 4.00 | 4.0704 | 1.76 | 0.30 | 0.2942 | –1.93 |
2 | 6% | 4.00 | 3.9132 | –2.17 | 0.30 | 0.3080 | 2.67 |
3 | 9% | 4.00 | 4.1824 | 4.56 | 0.30 | 0.3104 | 3.47 |
Table 2Crack identification of the fixed-free beam with double crack
Case | Error lever (%) | Crack location (m) | Crack depth () | ||||
Actual | Predicted | Error (%) | Actual | Predicted | Error (%) | ||
4 | 3 % | 4.00 | 4.0636 | 1.59 | 0.30 | 0.2945 | –1.83 |
8.00 | 8.1168 | 1.46 | 0.30 | 0.3035 | 1.17 | ||
5 | 6 % | 4.00 | 3.9016 | –2.46 | 0.30 | 0.3058 | 1.93 |
8.00 | 8.2312 | 2.89 | 0.30 | 0.2918 | –2.73 | ||
6 | 9 % | 4.00 | 4.1392 | 3.48 | 0.30 | 0.2893 | –3.57 |
8.00 | 7.7160 | –3.55 | 0.30 | 0.3092 | 3.07 | ||
5. Conclusions
This paper presents an analytical approach for determining the dynamic characteristics of cracked non-uniform beam carrying spring-mass systems by finite element method and illustrates a damage identification method which using hybrid neural genetic algorithm. And the following conclusions are acquired:
1) The effect of spring-mass system on the different order natural frequencies is different. And the natural frequencies of the cracked beam decrease with the increase of crack depth.
2) The crack diagnosis algorithm presented in this paper has strong anti-noise capability, which further illustrates the reliability and validity of this algorithm.
References
-
Tan G. J., Wang W. S., Jiao Y. B. Free vibration analysis of a cracked simply supported bridge considering bridge-vehicle interaction. Journal of Vibroengineering, Vol. 18, Issue 6, 2016, p. 3608-3635.
-
Ostachowitz W. M., Krawczuk M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. Journal of Sound and Vibration, Vol. 150, Issue 2, 1991, p. 191-201.
-
Tan G. J., Shan J. H., Wu C. L., Wang W. S. Free vibration analysis of cracked Timoshenko beams carrying spring-mass systems. Structural Engineering and Mechanics, Vol. 63, Issue 4, 2017, p. 551-565.
-
Zheng D. Y., Fan S. C. Natural frequencies of a non-uniform beam with multiple cracks via modified Fourier series. Journal of Sound and Vibration, Vol. 242, Issue 2, 2001, p. 701-717.
-
Zheng D.Y., Kessissoglou N.J. Free vibration analysis of a cracked beam by finite element method. Journal of Sound and Vibration, Vol. 273, Issue 3, 2004, p. 457-475.
-
Mehrjoo M., Khaji N., Ghafory-Ashtiany M. Application of genetic algorithm in crack detection of beam-like structures using a new cracked Euler-Bernoulli beam element. Applied Soft Computing Journal, Vol. 13, Issue 2, 2013, p. 867-880.
-
Jeyasehar C. A., Sumangala K. Damage assessment of prestressed concrete beams using artificial neural network (ANN) approach. Computers and Structures, Vol. 84, Issue 26, 2006, p. 1709-1718.
-
Dimarogonas A. D., Paipetis S. A., Chondros T. G. Analytical Methods in Rotor Dynamics. Applied Science Publishers, 1983.
-
Tan G. J., Wang W. S., Jiao Y. B., W. Z. G. Free vibration analysis of continuous bridge under the vehicles. Structural Engineering and Mechanics, Vol. 61, Issue 3, 2017, p. 335-345.
