Abstract
In order to grasp the nonlinear characteristics of high-speed spatial parallel mechanism, the bifurcation and chaotic behaviors of 4-UPS-RPS mechanism are analyzed. Firstly, the nonlinear elastic dynamic model of the mechanism is established by using the Lagrange equation and the finite element method. Then the effects of parameters including driving angular velocity, the radius of motion trajectory, the material of driving limbs, the diameter of driving limbs, and the mass of moving platform, on the bifurcation and chaotic behaviors of high-speed spatial parallel mechanism are studied. The results show that the above parameters all have a certain influence on nonlinear characteristics of the 4-UPS-RPS high-speed spatial parallel mechanism. The research can provide important theoretical basis for the further research on the non-linear dynamics of spatial parallel mechanism.
1. Introduction
With the development of modern industry, the requirement of the precision and dynamic performance of mechanical products is gradually increased. Nowadays, parallel mechanism has received more and more attention [1, 2]. Compared with the serial mechanism, parallel mechanism has the characteristics of high speed, high precision and no cumulative error. Chen et al. [3] analyzed the kinematics of 4-UPS-RPS spatial 5-DOF parallel mechanism. Liu et al. [4] studied the kinematics and dynamics of a spatial 3 degree-of-freedom parallel manipulator. Sun et al. [5] established a dynamic model of high-speed 6-PSS parallel robot and optimized the parameters of the mechanism.
There are a wide range of nonlinear factors in the mechanisms, such as clearance, dry friction, bearing oil film and nonlinear material constitutive relation [6-10]. As a seemingly irregular and random phenomenon, chaos is one of the most important nonlinear characteristic caused by nonlinear factors [11-14]. Recently, the chaotic behavior analysis of the mechanism is mainly focused on the time-delay system, vibro impact system, the mechanism with joint clearances and so on. G. I. Koumene Taffo et al. [15] studied the effects of time delay on the stability of the nonlinear oscillator and analyzed the heteroclinic bifurcation of the system by the Melnikov method. Wu et al. [16] analyzed the bifurcation and chaotic anti-control of a 3 degree-of-freedom vibro-impact system with clearance. Lu et al. [17] studied the influence of clearance to the steering swing system, and concluded that the pair clearance can make the swing system from the state of periodic motion, quasi periodic motion to chaotic motion gradually. As is known to all, nonlinear deformation of light components of high-speed parallel mechanism can cause complex chaotic behaviors, and worsen the dynamic performance of the mechanism. But up to now, the previous studies were focused on the nonlinearity caused by clearance, dry friction and bearing oil film, rarely involved the bifurcation and chaotic behaviors analysis of spatial high-speed parallel mechanism with nonlinear deformation of the limbs.
Therefore, the main purpose of this paper is to study the bifurcation and chaotic behaviors of spatial high-speed parallel mechanism, thus forecasting the dynamic behavior of the parallel mechanism and selecting appropriate system parameters of the mechanism. This paper regards 4-UPS-RPS high-speed spatial parallel mechanism as the research object. The nonlinear elastic dynamic model of the mechanism is introduced. The bifurcation and chaotic behaviors of the 4-UPS-RPS high-speed parallel mechanism with different parameters are analyzed by the phase diagram, the Poincare map, bifurcation diagram and the largest Lyapunov exponent method.
2. Description of high-speed spatial parallel mechanism
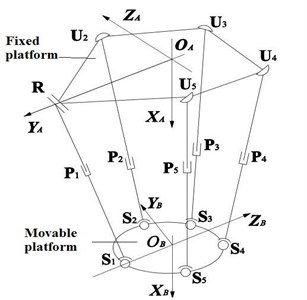
4-UPS-RPS (U represents hooke hinge, P represents prismatic pair, S represents spherical joint, R represents revolute pair) high-speed spatial parallel mechanism is shown in Fig. 1. The mechanism is composed of a fixed platform, a movable platform and five driving limbs. The fixed platform is connected with the movable platform by four UPS branch and a RPS. By changing the five driving limbs length, the movable platform can realize three-dimensional rotation and the two dimensional translation. The coordinate system of 4-UPS-RPS high-speed spatial parallel mechanism is shown in Fig. 2.
Fig. 1Mechanism diagram of 4-UPS-RPS
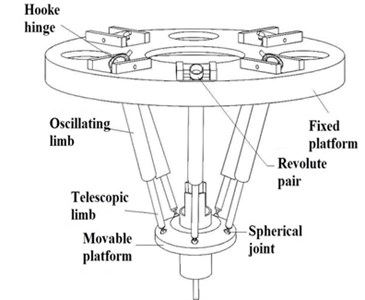
Fig. 2The coordinate system of 4-UPS-RPS
3. Nonlinear elastic dynamic model of high-speed spatial parallel mechanism
According to the Lagrange equation and the finite element method, the nonlinear elastic dynamic model of the spatial high-speed parallel mechanism is given by [18]:
where is the system total mass matrix, is the system total damping matrix, is the system total stiffness matrix, is the system total generalized force matrix, is the generalized coordinate of system, is the transfer matrix from system to driving limbs, is the transfer matrix from system to moving platform.
4. Bifurcation and chaotic behaviors analysis of high-speed spatial parallel mechanism
As we all known, we can judge whether the system is chaotic or not by observing the intercept point on the Poincare map [19, 20]. When the Poincare map is only one fixed point or a small number of discrete points, the system is in periodic motion. When the Poincare map is the limit cycle, the system is in almost periodic motion. When the Poincare map is stretches of dense point and having a fractal structure, the system is in chaotic motion [21].
Chaotic motion is very sensitive to the initial condition. Lyapunov exponents are a quantitative description of the indicators of this phenomenon [22]. When the Lyapunov exponent is negative in the direction, the phase volume is shrinkage, and the motion is stable. When the Lyapunov exponent is positive in the direction, the motion is in chaotic state. If the largest Lyapunov exponent (LLE) is positive, the system must be chaos. Therefore, the largest Lyapunov exponent of the time series can be used as a criterion for determining whether a sequence in a state of chaos [23, 24].
There are many methods for solving the largest Lyapunov exponent, such as the definition, the small data method, the Wolf method and the Jacobian method. The Wolf method is widely used in the research of chaos behaviors and chaotic time series prediction based on Lyapunov exponent [25-28]. The nonlinear elastic dynamic model shown in Eq. (1) is a set of coupled variable coefficient second order differential equations, and as everyone knows, this kind of dynamic model can be solved by Newmark integral method, and the Lyapunov exponent can be estimated by Wolf method [29]. Then in this paper, the Lyapunov exponent is estimated by Wolf method. The main calculation steps of Wolf method are as follows:
Step 1. Estimated average period by using fast Fourier transform.
Step 2. Estimated time delay and embedding dimension by using C-C method.
Step 3. Reconstructed phase space by using the time delay technique.
Step 4. Obtained the largest Lyapunov exponent by mapping the Lyapunov exponent chart and looked for stable region data.
The distribution of hinge of 4-UPS-RPS parallel mechanism is shown in Table 1. The basic parameters of 4-UPS-RPS parallel mechanism are shown in Table 2. The law of motion for 4-UPS-RPS spatial parallel mechanism is defined as (unit: rad, m):
Table 1The distribution of hinge of 4-UPS-RPS parallel mechanism (mm)
Hinge type | R | U2 | U3 | U4 | U5 | S1 | S2 | S3 | S4 | S5 |
Distribution radius | 717.07 | 645 | 645 | 645 | 645 | 202 | 202 | 202 | 202 | 202 |
Distribution angle | 0 | 0 |
Table 2The basic parameters of 4-UPS-RPS parallel mechanism
The length of oscillating limb | 760 mm | Elastic modulus of tension and compression | 2.0×1011 Pa |
The length of telescopic limb | 840.116 mm | Shear elastic modulus | 8.0×1010 Pa |
The cross section radius of telescopic limb | 20 mm | Poisson ratio | 0.29 |
The material of telescopic limb | Steel | The density of telescopic limb | 7.801×103 kg/m3 |
The material of moving platform | Aluminum alloy | The mass of moving platform | 36.28 kg |
Principal moment of inertia of unit cross section to -axis, -axis and -axis, respectively | 2.512×10-7 m4 | Moment of inertia of moving platform | 0.932 kg·m2 |
9.549×10-3 kg·m2 | |||
–1.937×10-2 kg·m2 | |||
9.549×10-3 kg·m2 | |||
1.256×10-7 m4 | 0.6735 kg·m2 | ||
8.43×10-4 kg·m2 | |||
1.256×10-7 m4 | –1.937×10-2 kg·m2 | ||
8.43×10-4 kg·m2 | |||
0.6816 kg·m2 |
4.1. Effect of driving angular velocity on the dynamic behavior of high-speed spatial parallel mechanism
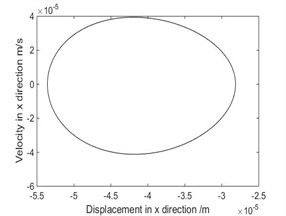
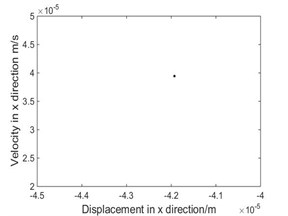
When the other parameters are invariant and 0.045, we change the values of the driving angular velocity, the phase diagram of the system in direction and the corresponding Poincare map are shown from Fig. 3 to Fig. 8. Bifurcation diagram of displacement with driving angular velocity is shown in Fig. 9.
Fig. 3The phase diagram and Poincare map when ω=π rad/s
a) Phase diagram
b) Poincare map
Fig. 4The phase diagram and Poincare map when ω= 4.712 rad/s
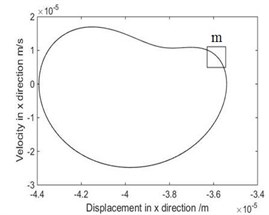
a) Phase diagram
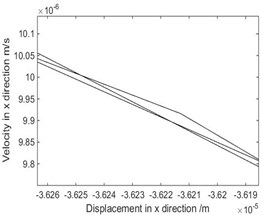
b) Local phase diagram of region
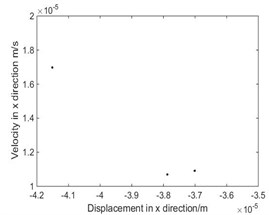
c) Poincare map
Fig. 5The phase diagram and Poincare map when ω= 9.2 rad/s
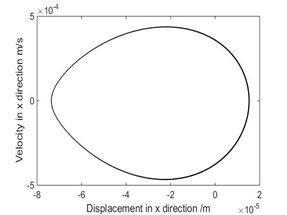
a) Phase diagram
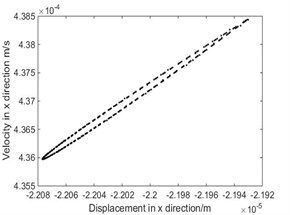
b) Poincare map
As shown in Fig. 3, when rad/s, phase diagram has only one trajectory and Poincare map has only one point, the system is in single-cycle motion. When is 4.712 rad/s, the system becomes unstable and bifurcates from single-cycle to 3-cycle. From Fig.4, when 4.712 rad/s, phase diagram has three tracks and Poincare map has three points, the system is in a state of three periodic motion. As shown in Fig. 5, when is 9.2 rad/s, phase diagram has many trajectories and Poincare map is a limit cycle, the system is in a state of almost periodic motion. From Fig. 6, when 9.35 rad/s, phase diagram has five tracks and Poincare map has five points, the system appears 5-cycle. As shown in Fig. 7, when 9.4 rad/s, the system is in a state of almost periodic motion. From Fig. 8, when 9.417 rad/s, the almost periodic ring is fracture, and the system is transferred from almost periodic motion to chaos, the phase trajectory of the system is not repeated and the Poincare map is a bit of dense points with fractal structure. The results show that the driving angular velocity has a great influence on the motion state of the system. When driving angular velocity is different, the system has different motion state. Overall, from Fig. 9, we could see the effects of driving angular velocity on chaotic behavior of the parallel mechanism.
Fig. 6The phase diagram and Poincare map when ω= 9.35 rad/s
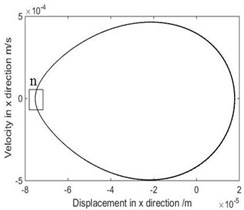
a) Phase diagram
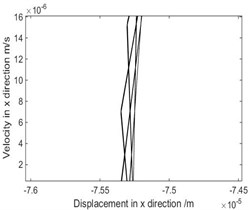
b) Local phase diagram of region
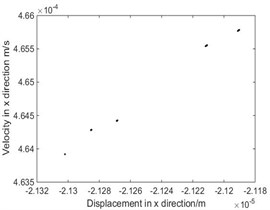
c) Poincare map
Fig. 7The phase diagram and Poincare map when ω= 9.4 rad/s
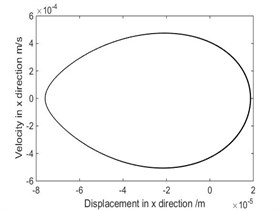
a) Phase diagram
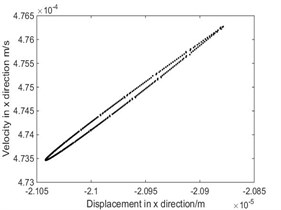
b) Poincare map
Fig. 8The phase diagram and Poincare map when ω= 9.417 rad/s
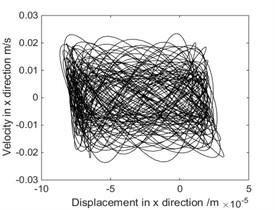
a) Phase diagram
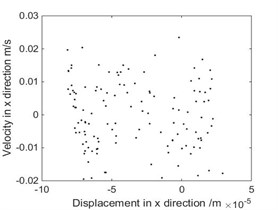
b) Poincare map
Fig. 9Bifurcation diagram of displacement with driving angular velocity
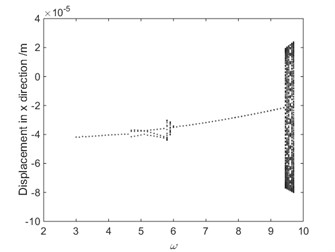
Fig. 10Bifurcation diagrams of largest Lyapunov exponent
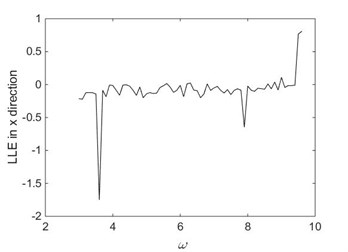
Fig. 11Lyapunov exponent chart in X direction
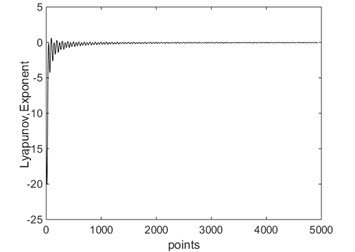
a) LLE = –0.2145 when rad/s
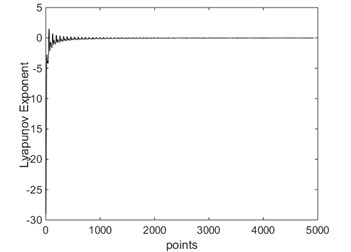
b) LLE = –0.1593 when 4.712 rad/s
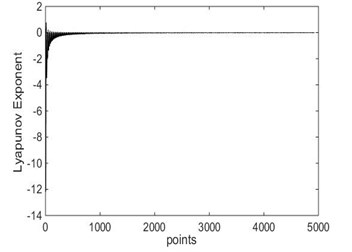
c) LLE = –0.0155 when 9.2 rad/s
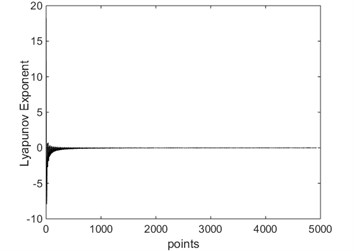
d) LLE = –0.0455 when 9.35 rad/s
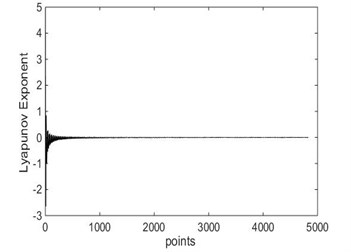
e) LLE = –0.0099 when 9.4 rad/s
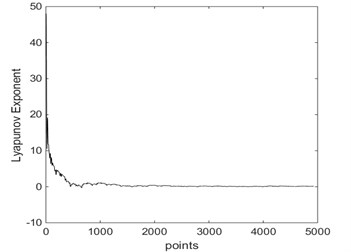
f) LLE = 0.7749 when 9.417 rad/s
Bifurcation diagrams of largest Lyapunov exponent is shown in Fig. 10. From Fig. 10, when 9.417 rad/s, the largest Lyapunov exponent in X direction is negative; when 9.417 rad/s, the largest Lyapunov exponent in direction is positive. The Lyapunov exponent diagram in direction corresponding to different driving angular velocity is shown in Fig. 11. From Fig. 11, when rad/s, 4.712 rad/s and 9.35 rad/s, the largest Lyapunov exponent in direction are –0.2145, –0.1593 and –0.0455, respectively. In these cases, the system is in a state of periodic motion. When 9.2 rad/s and 9.4 rad/s, the largest Lyapunov exponent in direction are –0.0155 and –0.0099, respectively. And the system is in a state of almost periodic motion. When 9.417 rad/s, the largest Lyapunov exponent in direction is 0.7749, the Lyapunov exponent is positive, therefore the system is in a state of chaos. As shown in Fig. 10 and Fig. 11, the driving angular velocity has a complicated influence on the chaotic behaviors of the 4-UPS-RPS high-speed parallel mechanism.
4.2. Effect of the radius of motion trajectory on the dynamic behavior of high-speed spatial parallel mechanism
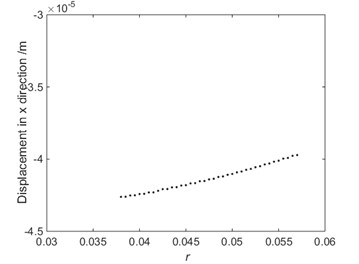
Due to the limitation of the workspace of the 4-UPS-RPS mechanism, the radius of motion trajectory denoted as is choosed from 0.038 m to 0.057m. When rad/s, bifurcation diagram of displacement with the radius of motion trajectory is shown in Fig. 12. From Fig. 12, the system is stable.
Fig. 12Bifurcation diagram of displacement with the radius of motion trajectory
4.3. Effect of the material of driving limbs on the chaotic motions of parallel mechanism
When 9.417 rad/s and 0.045, the largest Lyapunov exponent in direction of two different materials is shown in Fig. 13. If the driving limbs were aluminum, the largest Lyapunov exponent in direction is –0.2808. If the driving limbs were copper, the largest Lyapunov exponent in direction is –0. 1092. From Fig. 13, the system is stable.
Fig. 13Lyapunov exponent in X direction
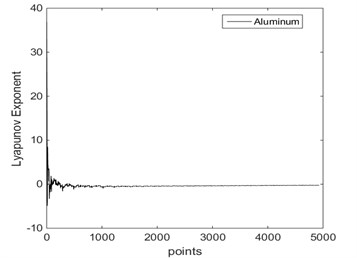
a) Aluminum
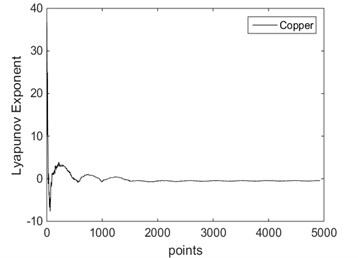
b) Copper
4.4. Effect of diameter of driving limbs and the mass of moving platform on the bifurcation and chaotic motions of parallel mechanism
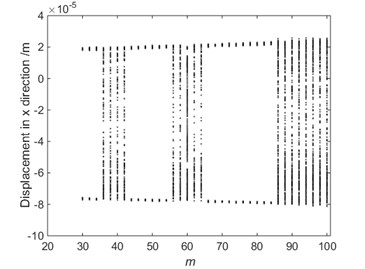
When 9.417 rad/s, 0.045 and the materials of the driving limbs was steel, the relationship between the LLE in direction and the diameter of driving limbs is shown in Fig. 14, the corresponding bifurcation diagram of displacement with the diameter of driving limbs is shown in Fig. 15. From Fig. 15, the system is in chaotic state. When 9.417 rad/s, 0.045 and the materials of the driving limbs was steel, the relationship between the LLE in direction and the mass of moving platform is shown in Fig. 16. The corresponding bifurcation diagram of displacement with the mass of moving platform is shown in Fig. 17. As shown in Fig. 17, the system is sometimes in periodic state and sometimes in chaotic state. From Fig. 14 to Fig. 17, the diameter of driving limbs and the mass of moving platform have a complex influence on the chaotic motions of the 4-UPS-RPS high-speed parallel mechanism.
Fig. 14The relationship between the diameter of driving limbs and the LLE in X direction
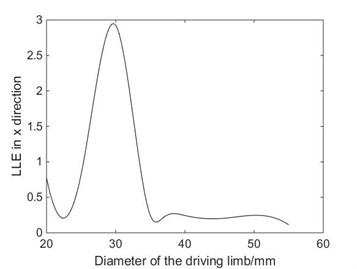
Fig. 15Bifurcation diagram of displacement with the diameter of driving limbs
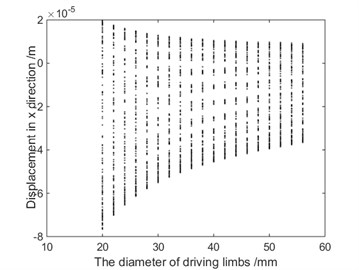
Fig. 16The relationship between the mass of platform and the LLE in X direction
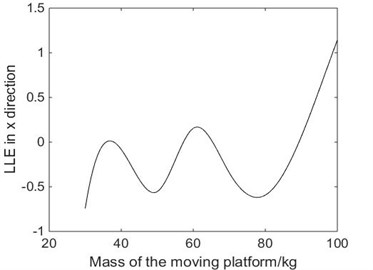
Fig. 17Bifurcation diagram of displacement with the mass of moving platform
5. Conclusions
This paper investigates the bifurcation and chaotic behaviors of 4-UPS-RPS high-speed spatial parallel mechanisms. The main conclusions are as follows:
1) The nonlinear elastic dynamics model of 4-UPS-RPS high-speed spatial parallel mechanism is introduced.
2) The effects of parameters including driving angular velocity, the radius of motion trajectory, the material of driving limbs, the diameter of driving limbs, and the mass of moving platform, on the bifurcation and chaotic behaviors of high-speed spatial parallel mechanism are studied by phase diagrams, Poincare map, bifurcation diagram and largest Lyapunov exponent, respectively. The results show that the above parameters all have a certain influence on the nonlinear characteristics of the 4-UPS-RPS high-speed spatial parallel mechanism.
3) The results show that the chaos phenomena can be avoided by selecting suitable control parameter, and therefore the motion property of mechanism is improved. The research can provide important theoretical basis for the further research on the nonlinear characteristic of 4-UPS-RPS high-speed spatial parallel mechanism.
References
-
Mei X., Tsutsumi M., Yamazaki T., et al. Study of the friction error for a high-speed high precision table. International Journal of Machine Tools and Manufacture, Vol. 41, Issue 10, 2001, p. 1405-1415.
-
Gao Lihua, Zheng Yaqing, Mitrouchev Peter Dynamic model of wire-driven parallel suspension system based on ADAMS. Journal of Shandong University of Science and Technology (Natural Science), Vol. 32, Issue 6, 2013, p. 89-94.
-
Chen Xiulong, Sun Xianyang, Deng Yu Kinematics analysis of 4-UPS-RPS spatial 5-DOF parallel mechanism. Transactions of the Chinese Society for Agricultural Machinery, Vol. 44, Issue 8, 2013, p. 257-261.
-
Liu Shanzeng, Yu Yueqing, Si Guoning, et al. Kinematic and dynamic analysis of a three-degree-of-freedom parallel manipulator. Journal of Mechanical Engineering, Vol. 45, Issue 8, 2009, p. 11-17.
-
Sun Xiaoyong, Zheng Bin, Baojie, et al. Parameter optimization design of high-speed 6-PSS parallel robot. Transactions of the Chinese Society for Agricultural Machinery, Vol. 46, Issue 5, 2015, p. 372-378.
-
Leine R. I., Wouw N. V. D. Stability properties of equilibrium sets of non-linear mechanical systems with dry friction and impact. Nonlinear Dynamics, Vol. 51, Issue 4, 2008, p. 551-583.
-
Manoj Mahajan, Robert Jackson, George Flowers Experimental and analytical investigation of a dynamic gas squeeze film bearing including asperity contact effects. Tribology Transactions, Vol. 51, Issue 1, 2008, p. 57-67.
-
Chang Jian C.-W. Bifurcation and chaos of gear-rotor-bearing system lubricated with couple-stress fluid. Nonlinear Dynamics, Vol. 79, Issue 1, 2015, p. 749-763.
-
González Cruz C.-A., Jáuregui Correa J.-C., Domínguez González A., et al. Effect of the coupling strength on the nonlinear synchronization of a single-stage gear transmission. Nonlinear Dynamics, Vol. 85, Issue 1, 2016, p. 1-18.
-
Yue Yuan Local dynamical behavior of two-parameter family near the Neimark-sacker-pitchfork bifurcation point in a vibro-impact system. Chinese Journal of Theoretical and Applied Mechainics, Vol. 48, Issue 1, 2016, p. 163-172.
-
Wang C. C., Hung J. P. Theoretical and bifurcation analysis of a flexible rotor supported by gas-lubricated bearing system with porous bushing. Journal of Vibroengineering, Vol. 18, Issue 3, 2016, p. 1934-1940.
-
Wang C. C. Non-periodic and chaotic response of three-multilobe air bearing system. Applied Mathematical Modelling, Vol. 47, 2017, p. 859-871.
-
Yang Xiaoli, Xu Wei Study on phase synchronization of stochastic chaotic system. Chinese Physics B, Vol. 17, Issue 6, 2008, p. 2004-2009.
-
Chun Biao A new procedure for exploring chaotic attractors in nonlinear dynamical systems under random excitations. Acta Mechanica Sinica, Vol. 27, Issue 4, 2011, p. 593-601.
-
Koumene Taffo G. I., Siewe M. Parametric resonance, stability and heteroclinic bifurcation in a nonlinear oscillator with time-delay: application to a quarter-car model. Mechanics Research Communications, Vol. 52, 2013, p. 1-10.
-
Wu Xin, Wen Guilin, Xu Huidong Anti-controlling Neimark-Sacker bifurcation of a three-degree-of-freedom vibration system with clearance. Acta Physica Sinica, Vol. 64, Issue 20, 2015, p. 89-96.
-
Lu Jianwei, Gujue, Wang Qidong Influence analysis of movement pair clearance on nolinear dynamic behavior of vehicle shimmy system. Journal of Mechanical Engineering, Vol. 44, Issue 8, 2008, p. 169-173.
-
Chen Xiulong, Li Yunfeng, Deng Yu, et al. Kineto elastodynamics modeling and analysis of spatial parallel mechanism. Shock and Vibration, Vol. 17, 2015, p. 1-10.
-
Goong Chen, Szebi Hsu, Jianxin Zhou Chaotic vibrations of the one-dimensional wave equation due to a self-excitation boundary condition. International Journal of Bifurcation and Chaos, Vol. 8, Issue 3, 1998, p. 447-470.
-
Qiu Chenlin, Cheng Li A chaotic analyzing method based on the dependence of neighbor sub-sequences in the data series. Acta Physica Sinica, Vol. 65, Issue 3, 2016, p. 48-63.
-
Niu Yujun, Wang Xingyuan, Nian Fuzhong, et al. Dynamic analysis of a new chaotic system with fractional order and its generalized projective synchronization. Chinese Physics B, 2010, Vol. 19, 12, p. 97-104.
-
Yang S. Quantitative analysis of unmanned ground vehicles trajectories based on chaos theory. Journal of Mechanical Engineering, Vol. 52, 2016, p. 2-127.
-
Zhang Yong New prediction of chaotic time series based on local Lyapunov exponent. Chinese Physics B, Vol. 22, Issue 5, 2013, p. 191-197.
-
Li Qingdu, Chen Shu, Zhou Ping Horseshoe and entropy in a fractional-order unified system. Chinese Physics B, Vol. 20, Issue 1, 2011, p. 175-180.
-
Dieci L., Vleck E. S. V. Lyapunov spectral intervals: theory and computation. Siam Journal on Numerical Analysis, Vol. 40, Issue 2, 2002, p. 516-542.
-
Fell J., Beckmann P. E. Resonance-like phenomena in Lyapunov calculations from data reconstructed by the time-delay method. Physics Letters A, Vol. 190, Issue 2, 1994, p. 172-176.
-
Diebner H. H., Sahle S., Mathias A. A robust, locally interpretable algorithm for Lyapunov exponents. Chaos Solitons and Fractals, Vol. 16, Issue 5, 2003, p. 841-852.
-
Dieci L., Russell R. D., Vleck E. S. V. On the computation of Lyapunov exponents for continuous dynamical systems. Siam Journal on Numerical Analysis, Vol. 34, Issue 1, 1997, p. 402-423.
-
Li Dongming Study on chaotic vibration of elastic linkage mechanism. Kunming University of Science and Technology, 2003.
About this article
This research is supported by the Natural Science Foundation of Shandong Province (Grant No. ZR2017MEE066), the Shandong Young Scientists Award Fund (Grant No. BS2012ZZ008).
