Abstract
In order to accurately and rapidly identify the vibration characteristic parameters of nonlinear stiffened plate structure, Rayleigh-Ritz method is used for modeling. First, the stiffened plate with four edges clamped is divided into plate and stiffeners. The plate is considered to be geometrically nonlinear, and the stiffeners are taken as Euler beams to solve the deformation energy and kinetic energy. Then, natural frequency of stiffened plate is solved by Rayleigh-Ritz method. Finally, stiffened plate structure in the laboratory is selected as the research object, results from Rayleigh - Ritz method calculation are compared with ANSYS and the swept frequency method results. The results show that the solution in this paper can be correct, which lays a good foundation for further nonlinear active control experiment.
1. Introduction
In order to improve rigidity and strength of plate, stiffened plate structure is wide used in industrial fields specially in the aerospace, shipbuilding and automobile industry. This structure has the advantages of light weight and high stiffness [1]. Therefore, in order to better understand the characteristics of the stiffened plate, it is necessary to analyze the vibration characteristics of stiffened plate.
At present, its results are seldom about the vibration analysis of the stiffened plate, and most of the results focus on FEM (Finite Element Method) software and experiment Method, the numerical method of stiffened plate is rare analyzed. Cho [2] proposed a method based on FEM and the assumed modal for the inherent modal analysis of stiffened plate structure, but there are still some deficiencies in this research of using FEM software methods, such as the serious distortion if the inappropriate element and mesh are selected. Liu [3] developed a method to study influence of the different arrangement forms of the stiffened rib for vibration of stiffened plate, Qiu [4] presented a method for the ultimate strength research for two-way orthogonal stiffened plate. Laser method, sweeping method of frequency, tapping method are frequent used in experiment, Li Xiao-jun [5], Li Shengquan [6], Hu Yuyong [7] respectively used sweeping method, laser method, tapping method to analyze vibration natural frequency of the stiffened structures. Although experimental method is relatively accurate, it is required the sensor of the reception test data pasted accurately, however, it is not easy that the sensor will be pasted on the appropriate location. For numerical method, Zhou [8] proposed a method based on analysis of stiffened plate structure of the difference method, N. Nguyen-Minh [9] developed a method to research free vibration of folded plate by cell smooth discrete shear gap, Zhong Ming [10] studied the rectangular plates from angle of theory, Ma Niujing [11] presented a analytical method of Lagrange equation for nonlinear free vibration of stiffened plate with four edges clamped. However, the reports of piezoelectric stiffened plates show that the calculating process of numerical calculation method could be often more complicated.
In view of these, Rayleigh-Ritz method was used to simplify numerical calculation of frequency analysis problem for the stiffened plate in this paper. Relative to other numerical methods, the Rayleigh-Ritz method is applied to the modeling of frequency analysis problem creatively. It makes the calculation process of the model simplified greatly. At the meantime, it can guarantee the correctness of the analysis process and provide theoretical basis for the engineering application and contrast of experimental analysis.
2. Vibration equation of stiffened plate
Stiffened plate structure is shown as Figs. 1-2, where , , respective represent the length, width and height of stiffened plate structure, width and height of stiffened plate structure, is neutral flexural function of the stiffened plate.
Fig. 1Structure of stiffened plate
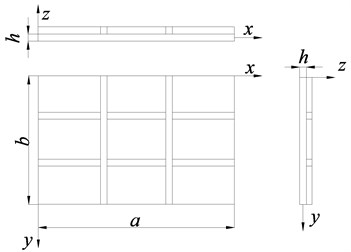
Fig. 2Reinforced bar structure
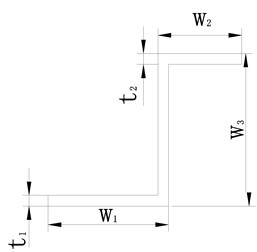
Table 1Related parameters of structure
Item | Plate (mm) | Reinforced bar(mm) | |
The reinforced bar of the -axis direction | The reinforced bar of the -axis direction | ||
600 | / | / | |
400 | |||
1.2 | |||
/ | 23 | 23 | |
19 | 16 | ||
26 | 28 | ||
2 | 2 | ||
2 | 2 | ||
72000 MPa | 72000 MPa | 72000 MPa | |
0.3 | 0.3 | 0.3 | |
2700 kg/m3 | 2700 kg/m3 | 2700 kg/m3 | |
Considering the nonlinear plate, the reinforced bar can be equivalent to Euler beam element [11], then the deformation energy of the reinforced bars can be expressed respectively:
where , , , – bending rigidity.
The kinetic energy of the reinforced bars can be expressed respectively:
Based on Rayleigh-Ritz method:
where , .
3. Analysis for stiffened plate by ANSYS and experiment
3.1. ANSYS analysis for stiffened plate
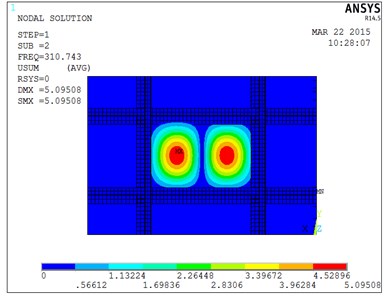
Unit type of the plate is Shell63, density of unit is 2700 kg/m3, elastic modulus is 72e9 Pa, Poisson’s ratio is 0.3. Through the horizontal and vertical line segment to form unit grid, the modal analysis results are shown as Fig. 3-4.
Fig. 3First mode of stiffened plate
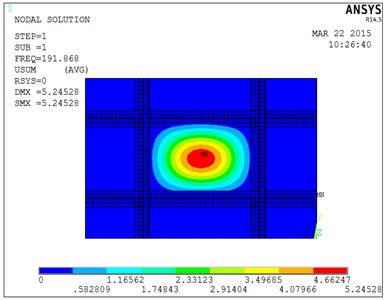
Fig. 4Second mode of stiffened plate
3.2. Experiment analysis for stiffened plate
Experimental system is showed as Fig. 5. Under sinusoidal sweep excitation signal of 0-500 Hz, piezoelectric acceleration sensor collected time domain signal as Fig. 6(a), then Fig. 6(b) is frequency spectrum analysis of Fig. 6(a).
Fig. 5The experimental system

Fig. 6Frequency domain graph
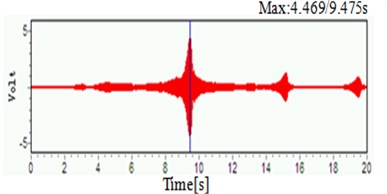
a) The time domain figure
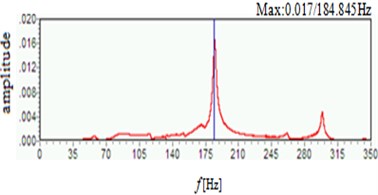
b) Frequency domain graph
Natural frequency results of the stiffened plate are shown in Table 2, these results include theoretical calculation, ANSYS analysis, experiment test three ways.
Table 2 shows that results from ANSYS and experimental would be bigger compared with theoretical calculation results, the main reason is that the impact on natural frequency of stiffened plate by smaller torsional rigidity could be ignored in order to simplify the complex calculation process [12-13]. Experimental results are also small compared with the ANSYS results, the main reason is that the boundary of the stiffened plate fixation couldn’t be fixed completely in the experiment. however, the ANSYS analysis process is the ideal conditions in boundary completely fixed.
Table 2Natural frequency of stiffened plate
Item | The first modal frequency (Hz) | The second modal frequency (Hz) |
Theory | 181.65 | 295.16 |
ANSYS | 191.87 | 310.74 |
Experiment | 184.845 | 298.795 |
4. Conclusions
The natural frequency of stiffened plates with four edges clamped is solved by Rayleigh-Ritz method. Its results compared with results of ANSYS and experiment showed that theoretical derivation from Rayleigh-Ritz method is correctness. Compared with other theoretical calculation methods, its calculation process is relatively simple. Rayleigh-Ritz method is appropriate for the theoretical calculation of the stiffened plate. It offers a new method for the frequency analysis of the stiffened plate, which avoids the high requirements for engineering experience and theoretical basis in the FEM analysis. Meanwhile, it offers contrast of result for the result of the experiment, and it also provides support for further nonlinear vibration active control experiment research.
References
-
Kevin Poulin C. Vibrations of stiffened composite plates with smart materials. Journal of Vibration and Acoustics, Vol. 126, Issue 3, 2004, p. 370-379.
-
Cho Dae Seung Forced vibration analysis of arbitrarily constrained rectangular plates and stiffened plates using the assumed mode method. Thin-Walled Structures, Vol. 90, Issue 5, 2015, p. 182-190.
-
Liu Yucheng, Wang Qingkui Computational study of strengthening effects of stiffeners on regular and arbitrarily stiffed plates. Thin-Walled Structures, Vol. 59, 2012, p. 78-86.
-
Qiu Ji Dong Research on Ultimate Strength of Two-way orthogonal Multi-stiffened Plates. Wuhan University of Technology, 2011.
-
Li Xiao Jun, Zhang Yu, Wang Yu Guo Determining natural frequency of high- speed train door system via scanning frequency excitation technique. Journal of Nanjing Institute of Technology, Vol. 2, 2011, p. 1-5.
-
Li Sheng Quan Composite Active Vibration Control for Smart Piezoelectric Structure Using Feed-forward Compensation. Nanjing University of Aeronautics and Astronautics The Graduate School College of Aerospace Engineering, 2012.
-
Hu Yu Yong, Lv Ming, Wang Shi Ying Measurement of material natural frequency and elastic modulus by knocking method. Mechanical Engineering and Automation, Vol. 5, 2011, p. 88-94.
-
Zhou X. Q. Band gap characteristics of periodically stiffened-thin-plate based on center-finite-difference-method. Thin-Walled Structures, Vol. 82, 2014, p. 115-123.
-
Nguyen Minh N., Nguyen Thoi T. Static and free vibration analyses of stiffened folded plates using a cell-based smoothed discrete shear gap method. Applied Mathematics and Computation, Vol. 266, 2015, p. 212-234.
-
Zhong Yang, Zhang Yong Shan Free vibration analysis of a thin plate with completely supported by finite cosine integral transform method. Journal of Ship Mechanics, Vol. 2, 2008, p. 305-310.
-
Ma Niu Jing, Wang Rong Hui Nonlinar free vibration of stiffened plate with four edges clamped. Chinese Journal of Theoretical and Applied Mechanics, Vol. 5, 2011, p. 922-930.
-
Cao Zhi Yuan Theory of Plate and Shell Vibration. China Railway Publishing House, Beijing, 1989.
-
Prathap G., Varadan T. K. Large amplitude flexural vibration of stiffened plates. Journal of Sound and Vibration, Vol. 57, Issue 4, 1978, p. 583-593.
About this article
National Natural Science Foundation of China (No. 51305003), Foundation of Anhui University of Science and Technology (No. 2016yz004).
