Abstract
Components in engineering systems are degenerated due to different conditions. In order to avoid serious loss, the components need to be replaced before failure occurs to provide the intended and safe operation of the systems. Therefore, the maintenance decision-making method based on remaining useful life considering different optimal targets was presented in this paper, and the purpose of this method was to find an optimal choice of maintenance actions to be performed on a selected group of machines for engineering systems. Then, the optimal maintenance interval based on the minimum expected cost rule was discussed, and the arithmetic reduction of intensity model was introduced to describe the influence of remaining useful life. Finally, a full life experiment of gearbox was given to demonstrate the preferred decision-making with the influence of the remaining useful life.
1. Introduction
As the reliability of complex machine is decreasing with the increasing of its service age, randomly failures unavoidably occur during the production process [1]. Maintenance decision-making is the study of modeling and parameter optimization under different maintenance strategy target. The concept that maintenance decision-making is proposed and the process is already analyzed [2]. Then its characteristics were analyzed, and the key relationship of maintenance contents and decision-making process were proposed [3]. Therefore, the maintenance decision method was proposed in the application of complex equipment [4-6].
In addition, a lot of new methods for maintenance decision-making are proposed to extend its application field. For example, taking the reliability centered maintenance (RCM) into maintenance decision, so maintenance decision mode is used in nuclear power field [7]. A method is to be put forward to make the maintenance decision for long-term reserved equipment [8]. Decision making methods are proposed based on the proportional intensity model for engineered systems [9].
In this paper, we will study the maintenance decision-making method due to the minimum expected cost rule, maximum expected availability rule and expected risk rule with the influence of remaining useful life.
2. Maintenance decision-making based on remaining useful life
Maintenance decision-making is the final step of condition based maintenance (CBM), which also is the fundamental aim of remaining useful life prediction. In maintenance decision-making, we always want to make the minimum of the economic cost of components to achieve maximum profits under the condition of safety and task availability. Therefore, the decision goal of cost model based on economy is the minimum cost to determine the maintenance interval. Cost target in the actual situation is generally measured by the average cost during the same time, which is equal to the cost divided by the time. The time proposed in this paper is a general concept which can describe mileage, calendar time and so on.
The component failure is random, so the number of failure and the number of preventive maintenance is uncertain during a period of time, which makes the cost during the same time is difficult to acquire. The time that between new components or components after repair start work and the next failure is called a cycle. According to the theory of renewal process, the average cost can be represented with a cycle when the component works long enough, which can be described as:
In the cost model based on economy, we usually take the minimal average cost as objective function. When running time is long enough, the average cost can be described as:
where is sum of all cost in a cycle and is the length of update cycle.
In a cycle, the total cost is mainly composed by three parts, which are the state monitoring cost, preventive maintenance cost and corrective maintenance cost. Therefore, the total cost of a cycle is shown as:
where is the cost of preventive maintenance before function failure, is the repair cost after the failure occurs, in general , is the production loss during the same time because of maintenance, is the average cost for component status monitoring, is the optimal maintenance interval after the monitoring, is the moment for the th monitoring of component, is the average time for preventive maintenance and is the average time for corrective maintenance.
The time of a cycle can be defined as:
In conclusion, cost model based on economy can be obtained:
Once the probability density function (PDF) of remaining useful life is obtained, we can get via Eq. (5). Therefore, the minimum maintenance cost and the next maintenance interval of component can be obtained. The monitoring data is updated over time, so the remaining useful life information can also get updated. As a result, the optimal maintenance interval is dynamic change.
The time for preventive maintenance and corrective maintenance is far less than the monitoring time during the maintenance of component, so it can be ignored. In the process of CBM, the money for instruments that used for component condition monitoring is cost already. So, the monitoring cost is negligible compared to the cost for preventive maintenance and corrective maintenance in every condition monitoring process. Therefore, in the process of maintenance decision-making, it can be ignored, which means .
At the current time , if the minimum average cost during the same time appears between two monitoring time (solid line), it demonstrates that preventive maintenance cost is the lowest at time . On the other hand, if the minimum average cost during the same time is not between two monitoring time (dashed line), it means that it is not the best time for maintenance. In this situation, the component needs not to be repaired until the next new monitoring point to make maintenance decision again. As shown in Fig. 1.
Fig. 1Sketch map of optimized maintenance time
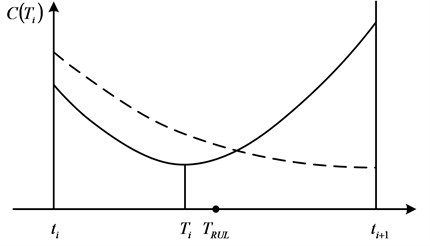
During the maintenance decision-making, we must consider the influence of the remaining useful life. When the maintenance interval obtained via cost model is earlier than component remaining useful life , the result of cost model based on economy can be used for maintenance decision-making. On the contrary, if the maintenance time is later than the remaining useful life, it means that component failure has occurred before next monitoring point, therefore maintenance decision-making is obtained according to the remaining useful life.
3. Application and the results
3.1. The full life experiment of gearbox
The gearbox is compact in structure and precision in output, which is widely used in the transmission system of mechanical equipment. In this paper, the full life experiment of a gearbox is carried out, and its remaining useful life is obtained by the particle filter. The test bed is shown in Fig. 2. The remaining useful life is given as the form of PDF, which the detail is not discussed in this paper. The truth and estimation of remaining useful life in every monitor point is shown in Table 1.
Fig. 2The test bench
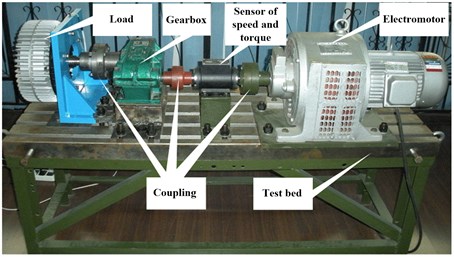
Table 1The truth and estimation of remaining useful life in every monitor point
Monitoring time | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
(h) | 362 | 322 | 282 | 242 | 202 | 162 | 122 | 82 | 42 |
Prediction of RUL (h) | 435 | 383 | 306 | 269 | 211 | 183 | 145 | 128 | 61 |
3.2. The maintenance decision-making for gearbox
In order to achieve the maintenance decision-making for gearbox, the average time for preventive maintenance is 5 hours, the average cost of preventive maintenance is 1000 RMB, the average time for corrective maintenance is 15 hours, the average cost of corrective maintenance is 2000 RMB. In addition, assuming that 200 RMB and 100 RMB. Finally, the risk is 0.05 for the risk model.
The maintenance decision-making based on cost model is carries on firstly. The optimal maintenance interval and the corresponding maintenance cost is obtained via Eq. (5), which is shown in Fig. 3.
Fig. 3Maintenance decision based on cost model. Symbol * is the minimum point of the curve on the plane
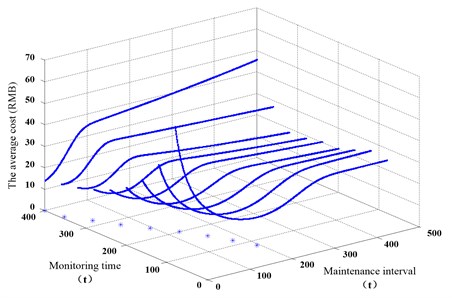
As we can see, maintenance cost changes dynamically over time with each monitoring point. The minimum of the maintenance cost can be obtained, so that we can determine the optimal maintenance interval. Taking the maintenance decision-making at time 350 h as an example, the curve of 350 h has reached the minimum value in 10 hours as shown in figure, which demonstrates that repair at time 360 h will make the cost lowest. As shown in Table 1, the remaining useful life of gearbox is about 400 hours, so repair based on maintenance decision-making will be taken before the fault occurs to decrease the maintenance cost.
Table 2Maintenance result based on cost model
Monitoring time | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
(RMB) | 20.67 | 19.41 | 17.67 | 15.35 | 13.32 | 12.38 | 11.61 | 12.25 | 14.78 |
(h) | 196 | 177 | 155 | 39 | 98 | 73 | 42 | 9 | Repair immediately |
(h) | 362 | 322 | 282 | 242 | 202 | 162 | 122 | 82 | 42 |
Prediction of RUL (h) | 435 | 383 | 306 | 269 | 211 | 183 | 145 | 128 | 61 |
The optimal maintenance interval for individual monitoring point based on cost model is shown in Table 2. It can be seen that there is deviation between the optimal maintenance interval and the actual remaining useful life. This is because that the cost model is used to balance corrective maintenance cost and preventive maintenance cost with the purpose of minimizing the maintenance cost, rather than make full use of the remaining useful life. So, the deviation is reasonable. It demonstrates the effectiveness of the proposed model that repairing before component fault occurs.
4. Conclusions
In this paper, the method of optimal maintenance decision-making for engineered systems considering the remaining useful life is proposed. The optimal maintenance interval respectively based on the minimum expected cost rule, maximum expected availability rule and expected risk rule is formulated. In addition, a gearbox full life experiment is carried out to demonstrate the availability of the proposed method. Meanwhile, the relationship of optimal maintenance interval and the remaining useful life is discussed. The consideration of the remaining useful life can be important for accurately estimating the optimal maintenance interval for the engineered systems.
References
-
Liu Fanmao, Zhu Haiping, Liu Boxing Maintenance decision-making method for manufacturing system based on cost and arithmetic reduction of intensity model. Journal of Central South University, Vol. 20, 2013, p. 1559-1571.
-
Guo Jinmao, Zhang Yaohui, He Rui, et al. The process of mission based maintenance decision-making for material. The 3rd International Conference on Maintenance Engineering, Chengdu, China, 2012.
-
Huang Jianxin, Bian Yaqin, Li Shubin Condition-based maintenance decision-making for Equipment. Journal of Donghua University, Vol. 25, 2008, p. 201-207.
-
Rosmaini Ahmad, Shahrul Kamaruddin An overview of time-based and condition-based maintenance in industrial application. Computers and Industrial Engineering, Vol. 63, 2012, p. 135-149.
-
Cui Yan, Chen Shijun, Qu Meng Research and application of maintenance decision method of complex equipment in nuclear power plant. Journal of Donghua University, Vol. 33, Issue 2, 2016, p. 252-256.
-
Jouin CMarine, Gouriveau Rafael, Hissel Daniel, et al. Particle filter-based prognostics: Review, discussion and perspectives. Mechanical Systems and Signal Processing, 2015.
-
Huang Lijun, Chen Yu, Ma Yijin, et al. Reliability-centered maintenance-based maintenance decision in new nuclear power plants. Journal of Donghua University, Vol. 33, Issue 2, 2016, p. 248-251.
-
Xu Ying, Su Jingjing, Yang Jun The maintenance decision-making for long-term reserved equipment based on the failure data. The 2nd International Conference on Materials Science and Manufacturing, Zhangjiajie, China, 2013.
-
Rong Xiang, Zuo Hongfu Condition-based maintenance decision making methods for civil aeroengine. Transactions of Nanjing University of Aeronautics and Astronautics, Vol. 133, Issue 3, 2011, p. 1-11.
