Abstract
This paper presents a design, a numerical analysis, a build-up and dynamic testing of an engineered and fabricated wheel with a passive vibration damping system designed for a roller coaster system. Taking into account the limited amount of space for fixing a wheel to a roller-coaster, this study shows an approach in which a special wheel design and viscoelastic inserts are used to reduce vibrations. A wheel comprises a rim and hub separated by a viscoelastic material and simultaneously connected by using spring steel fasteners with contractions ensuring elasticity. The dynamic tests of the wheel with a passive vibration damping system were completed with an assessment of the vibration reduction ratio in comparison to conventional roller coaster wheel types currently operated at the amusement park Energylandia located in Zator, Poland. Laboratory test results show reduction of vibrations by 36 % in the low frequency range, by 63 % in the medium frequency range and by 45 % in the high frequency range.
1. Introduction
This paper concerns the design engineering and dynamic testing of a prototype wheel with a passive vibration damping system intended for operation on a roller coaster vehicle. Ultimately, the solution presented herein is intended to replace roller coaster wheels without vibration damping systems. Roller coasters are performance rail vehicles operated for the purpose of moving people at considerable speed along a contorted track at amusement parks. The main components of a roller coaster system are an elevated railway track assembly and a subsystem of wheel assemblies [1-3], which run on the track; due to the arrangement of the running track system, the vehicle performs acrobatic manoeuvres while following the track system (Fig. 1).
Fig. 1Design of the “Mega-Coaster” being built at the Energylandia amusement park in Zator (Poland)

The wheel of a roller coaster is a critical system component, since it interfaces the track rail with the roller coaster car that the wheel assembly is installed on [1]. Fig. 2 shows an example of a typical wheel with an overview and a cross-section. Given that each roller coaster car is intended to carry passengers, each wheel must meet specific (and high) safety standards. Given the characteristics of a roller coaster motion on the track, the wheels are subject to dynamic loads, which include vibration loads. These load types affect the structural strength and material fatigue of the wheels, leading to the propagation of structural component wear, mainly of the rolling bearings. The concomitant vibration phenomena cause some of the negative sensations experienced by roller coaster passengers – the overall riding comfort is reduced, and other effects include audible sound waves. Moreover, the vibration phenomena tend to dissipate the kinetic energy of the roller coaster car and reduce the speed of its motion on the track [4].
Fig. 2Solid wheel: a) overview, b) cross-sectional view, c) actual wheel

a)
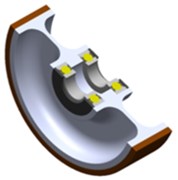
b)

c)
One of the most important factors which inhibit the building of increasingly higher and faster roller coasters are the wheels, or rollers. Therefore, it is prudent to investigate the wheel designs and materials of which the wheels are made. Three types of safety wheels are used to secure roller coaster cars running along tracks (Fig. 3): (1) loaded tractor (or running) wheels, which carry the roller coaster car weight, (2) side friction wheels, which act as guiding rollers mounted square to the running wheels, and (3) underfriction (or up-stop) wheels, which hug the track rail bottom to prevent the roller coaster car from coming off the track.
Fig. 3Wheel assembly of a roller coaster

The design of the wheel for a high-speed roller coaster car must meet four primary requirements [1]: low rolling resistance, high strength, high durability, and vibration damping.
A major requirement that roller coaster passengers expect to be met is vibration reduction for improved riding comfort. Vibrations contribute to bearing wear, loosening of track parts, increased kinetic energy dissipation, reduced roller coaster car speed, etc. The vibration phenomena in a roller coaster system have several root causes. Firstly, an elevated track system is a large steel structure encumbered by inherent dimensional deviations and misalignment of track components. Secondly, the track is exposed to fouling; if it is present, the wheels must traverse various rough spots and smoothness imperfections, resulting in vibration. Vibrations caused by track fouling are eliminated by soft wheel tires; however, the softer a wheel tyre is, the higher the rolling resistance becomes.
A roller coaster system is a complex object comprising a large number of interfaced elements. Any attempt at a precise description of its properties would require physical and mathematical models with many degrees of freedom. When in motion, each roller coaster car is loaded with multiple external inputs from track surface irregularities, the resilience of the track and its load-bearing structure, forces of inertia during the manoeuvring of the roller coaster car, system play, etc. Building a model which considers all of the properties of this system and active inputs is a very difficult problem to solve. It would be extremely challenging to produce analytical solutions for this system, if not outright impossible. Due to the coupling of many phenomena in a roller coaster system, it is difficult to provide any conclusions from model tests. Complex analysis is avoided in testing a system of this type by favouring simplified models, which help to assess the effects of selected parameters or design modifications in singular elements on the dynamic performance of the entire system [5]. A reference research [6] suggests that conclusions established from analysing simplified models show concurrence with the behaviour of more complex systems. Hence research testing is focused on analysing the dynamic properties of a single wheel with a passive vibration damping system. The references [1-4, 7] allow the conclusion to be drawn that improving the vibration isolation performance of a single wheel will reduce the vibration levels acting on the roller coaster car that the wheel is a component of.
In order to reduce unfavourable vibration-related phenomena, two different approaches are basically applied in vehicles of various types. The traditional approach consists in providing a correct suspension system containing necessary damping elements [8, 9]. The innovative approach consists in providing vibration damping elements in a driving wheel itself. This solution demonstrates two basic advantages, i.e. vibrations are attenuated quite closely to their generation source, and, in contrary to the traditional approach, no large space is required to fix damping elements. Solving the problem of damping vibrations by elaborating special designs of driving wheels has been the subject matter of study papers published over the last few years. In their paper [10], the authors presented a solution based on introducing one metre of viscoelastic inserts in the wheel structure which disperse the energy of vibrations due to deformations. In another paper [11], the authors examined properties of rubber materials used as inserts pressed between discs and rims of rail vehicle wheels in order to reduce vibrations. Conclusions resulting from these studies show that using springy wheels with elastic inserts has a positive impact on reduction of vibrations by dispersing their energy.
Taking into account the limited amount of space for fixing a wheel to a roller-coaster, this study shows an approach in which a special wheel design and viscoelastic inserts are used to reduce vibrations.
2. Design principle and test rig description
The wheel was designed according to Patent Application ref. P.420895 (filed with the Polish Patent Office) concerning the invention of a vibration reducing wheel intended for operation in recirculating motion machines categorized as roller coasters. The Patent Applicant is the company ENERGY 2000 Sp. z o.o. The design principle was established from the characterization of the invention and the following operating conditions of the invented wheel:
– wheel load range: 0-2070 N,
– wheel rotation angular velocity range: 0-190 rad/s (equivalent to a roller coaster car speed range of 0-110 km/h),
– wheel vibration frequency range: 0-5000 Hz.
Given the occurring vibration ranges, they were divided into the following:
– low-frequency vibrations from 2 to 18 Hz, sensed by roller coaster car passengers, since this is a resonance frequency range for most systemic organs in humans [12],
– medium-frequency vibrations from 18 to 2000 Hz, sensed by and audible to passengers,
– high-frequency vibrations from 2000 Hz and up, which are audible to, yet poorly sensed by roller coaster car passengers.
All frequency values in the three ranges cause structural fatigue effects. The testing contemplated herein was focused on reducing the vibration amplitude in all three vibration frequency ranges. To assure an impartial assessment of the design principle, factors were defined to assess the vibration reduction ratios resulting from the application of the wheel with a passive vibration damping system. The definitions of the factors first required a specification of the measured vibration values and their expression. A measured vibration signal can be interpreted in physical terms as acceleration which is expressed by a data series in a discrete time domain , with the discrete time domain defined as follows: , and is the sample number, is the sampling frequency, is the total number of samples in the data series. It was more convenient to operate with the notation , which represents a discrete series of measurement data at . A discrete Fourier transform was defined as follows for a sample series :
where: is the number output component of the discrete Fourier transform, while is the total number of samples in the data series and the number of frequency points in the acceleration spectrum.
The vibration reduction was assessed with an effective vibration reduction ratio over a specific frequency band. The effective vibration reduction ratio was defined as follows:
where and are the effective vibration values defined as:
where: is the frequency band number (for the frequency band is 2-18 Hz, for the frequency band is 18-2000 Hz, for the frequency band is 2000-5000 Hz), is the spectrum component number approximately corresponding to the lower limit of the number frequency band, is the spectrum component number approximately corresponding to the lower limit of the number frequency band, is the spectrum of the signal , is the spectrum of the signal , is the acceleration of a specific structural point in operation with the wheel with the vibration damping system, is the acceleration of a specific structural point in operation with a solid wheel. The effective vibration reduction ratio is the percentage change of the effective vibration value in the number frequency band for the wheel with the vibration damping system in relation to the performance of a solid wheel.
A test rig (Fig. 4) was designed and built for the tests and to enable dynamic testing. The test rig enables testing by analysing the vibration levels present during the rotational motion of a roller coaster wheel at speed and load values emulating the operating conditions of actual roller coaster systems. The test rig comprised: a stationary carrier frame, 1 a 3-kilowatt, 2840 RPM three-phase motor with a 2 belt pulley on the shaft, a 2-3 belt transmission with a reduction ratio of , a 4 m driving pulley shaft, a 6 moving frame with a shaft on which the 5 tested wheel was mounted, the wheel featured a diameter of m, and a 7 load at the end of the moving frame. The frequency of rotation of all components in the system can be expressed as a function of the (1) motor shaft rotational frequency, i.e. , with being the motor shaft RPM (revolutions per minute). The 2 belt pulley rotational frequency is , whereas the rotational frequency of the 3 belt pulley and the 4 driving pulley is The 5 tested wheel rotational frequency is , which granted the required wheel angular velocity at the rated speed of the test rig motor.
Fig. 4Test rig: a) the design, b) an overview, c) a kinematic diagram
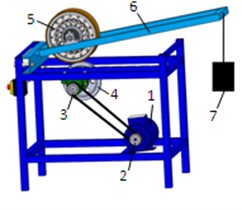
a)

b)
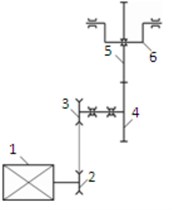
c)
The station design facilitates providing a wheel with correct load 7 of value located at the end of frame 6. One end of the frame (point A) is pivotally connected to the station body, and the other end (point C) remains free. The tested wheel is fixed between these points.
Fig. 5Diagram of station geometry and load
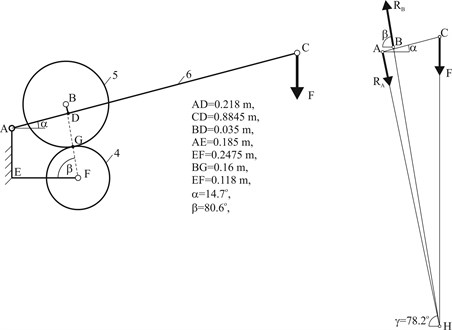
While analysing the frame as a flat lever-type system, it can be stated that it is affected by three forces, i.e. load, force of reaction in the wheel fixing point B and force of reaction in the pivot A. While considering these forces, it is must be stated, on the basis of the theory of mechanics, that they remain in equilibrium, on condition that they create a convergent system. The direction of the force is vertical and the direction of the force of reaction results from the system geometry. Namely, the line of force passes through points B, G and F. The third force, i.e. , must be routed in such a manner that its line is convergent to lines of forces and in point H. When angles , and are known, it is possible to derive the force equilibrium equations:
and use them to determine the relation between the force of value transferred by a bearing onto a wheel in point B and load as:
Application of a lever mechanism resulted in obtaining almost fivefold velocity ratio. Obviously, such a relation between load and force takes place in static equilibrium conditions. In dynamic conditions, due to vibrations, this relation is disturbed by dynamic phenomena, as wheels 4 and 5 freely come in contact. Similar conditions are present during roller-coaster wheel movement on a track where static loads are complemented with vibration-type dynamic phenomena, and the wheel-track contact is free.
3. Design and production of the wheel with the vibration damping system
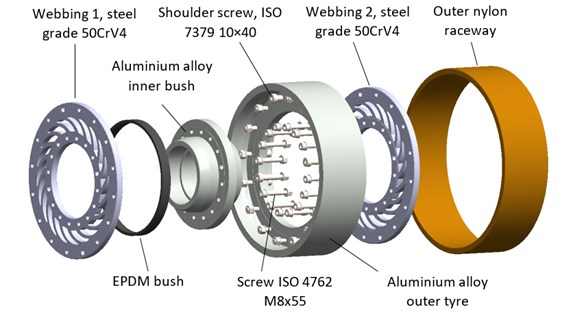
Fig. 6 shows an overview and a cross-sectional view of the designed wheel with the vibration damping system, and the components of the wheel assembly.
Fig. 6Wheel with the vibration damping system: a) overview, b) cross-sectional view, c) wheel components

a)

b)
c)
Static endurance simulations using the FEM were conducted for the designed driving wheel, with the view to determining deflections and stresses in individual system elements and selecting correct thickness of a fastener. Deflections are important for operation of flexible elastomer inserts, as presence of such inserts with insufficient deflections does not have any significant impact on vibration damping. On the other hand, due to endurance-related issues, stresses in material must not be excessive.
A wheel placed on a track was provided with a static load equal to 2070 N applied to the wheel shaft, and the applied model of the wheel-track contact assumes no penetration. The node mesh and the wheel loading method chosen are shown in Fig. 7.
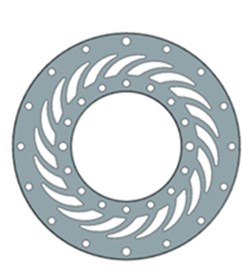
A key contributor to the vibration isolation performance of the wheel with the vibration damping system was the webbing of the wheel, aside from the resilient bush. The most important geometric parameters of the wheel webbing were the webbing thickness and the shape of the webbing slots. The designed wheel webbing is shown in Fig. 8, with a single webbing slot geometry highlighted. The wheel webbing featured twenty slots intended to add resilience so that the inner bush and the outer tyre could move relative to each other.
The resilience of the wheel webbing depended on the webbing thickness; hence, the wheel webbing design selection was first narrowed down by completing a numerical analysis of displacement, stress and deformation of the entire wheel with the vibration damping system featuring different wheel webbing thickness values: 6, 8, 10, 12, 14, and 16 mm. The load was 2,070 N. The selected test results are shown in Tables 1 and 2. A numerical analysis of frequency was also carried out for each of the wheel webbing thickness values shown above, and the resonance frequency values produced are listed in Table 3.
Fig. 7Assumed node mesh and the wheel loading method
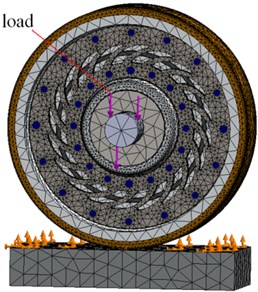
Fig. 8Designed webbing of the wheel with the vibration damping system: a) overview, b) geometry of a single slot of the wheel webbing
a)
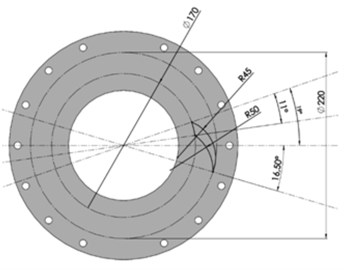
b)
The results of numerical analyses qualified a 12 mm thick wheel web as feasible for use in an actual system. This thickness was a compromise between the wheel resilience desired (as determined by the riding comfort of roller coaster passengers) and the required wheel strength. A lower wheel webbing thickness resulted in excessive deformation of the resilient bush, ultimately leading to it being forced out of the wheel assembly. A higher wheel webbing thickness made the wheel overly hard, minimizing the vibration isolation performance of the resilient bush. The frequency analysis showed that the resonance frequency values of the wheel designed with the vibration damping system and a 12 mm thick webbing would fall within ranges similar to those of solid wheels previously in operation.
Based on the design explained herein, the specific components of the wheel with the vibration damping system were fabricated and are shown in Fig. 9(a). The inner bush and the outer tyre were fabricated in order to install the wheel with the vibration damping system as a direct replacement of a solid wheel in the wheel assembly of a roller coaster car without any need for modifying the car design. Fig. 9(b) shows the complete object, which was the wheel with the vibration damping system fabricated for the tested design.
Table 1Displacement, stress and deformation of the wheel with the vibration damping system for 12 mm wheel webbing thickness
Scale of displacement | Scale of stress | Scale of deformation |
 |  |  |
Distribution of displacement | Distribution of stress | Distribution of deformation |
 |  |  |
Table 2Maximum displacement and stress values for an assembled wheel with the vibration damping system relative to the webbing thickness
Webbing thickness, mm | Max. displacement, mm | Von Mises max. stress, N/m2 |
6 | 0,010 | 34731328 |
8 | 0,0092 | 23808770 |
10 | 0,0087 | 20029782 |
12 | 0,0085 | 17654744 |
14 | 0,0082 | 15293037 |
16 | 0,0081 | 13067882 |
4. Laboratory performance testing of the wheel with the vibration damping system
The first stage of experimental testing was to determine the natural frequency values of the tested wheels. To accomplish this, a test was completed to measure the vibration levels under pulse inputs in a solid wheel and a wheel with the vibration damping system. The theory of mechanical vibration assumes that a Dirac pulse input applied to a system excites all natural frequencies inherent to that system. The acceleration spectrum of vibration excited by a pulsed input is shown in Fig. 10. The acceleration spectrum helped to identify the natural vibrations of the tested rollers. They are listed in Table 4.
Table 3Resonance frequency values of the wheel with the vibration damping system for various thickness values of the wheel webbing
Frequency no. | Webbing thickness, mm | |||||
6 | 8 | 10 | 12 | 14 | 16 | |
Natural frequency, Hz | ||||||
1 | 852 | 912 | 981 | 1050 | 1120 | 1180 |
2 | 1116 | 1177 | 1258 | 1346 | 1442 | 1534 |
3 | 1190 | 1270 | 1350 | 1432 | 1520 | 1604 |
4 | 1784 | 1821 | 1834 | 1832 | 1822 | 1806 |
5 | 2610 | 2672 | 2745 | 2820 | 2895 | 2971 |
6 | 2900 | 2960 | 3000 | 3022 | 3035 | 3040 |
7 | 3900 | 4002 | 4080 | 4144 | 4195 | 4237 |
Fig. 9Wheel with the vibration damping system: a) components: 1 – inner bush, 2 – outer tyre, 3 – webbing, 4 – bearing assembly, 5 – outer wheel raceway polymer material, 6 – thin resilient bush, b) an assembled wheel with the vibration damping system

a)

b)
The range of frequency of on-board wheels must be somehow explained. Let us assume that, in the event of any possible single defect in the wheel race, excitation coincides with each wheel turn, which, at the permissible speed of the designed wheel, generates excitations of frequencies up to 30 Hz. If there are more such defects or a track is rough in numerous locations, the range of excitation frequency can be multiplied. Thus, roller-coaster wheels are designed in such a manner that native frequencies of wheels are quite high, but definitely never overlap the range of human organ native frequency. This prevents excessive excitation of frequencies unpleasant for passengers, in case wheel defects or rough track sections are present. The analysis of characteristics presented in Fig. 10 shows that the driving wheel has been designed correctly.
Table 4Natural vibrations of the solid wheel and the wheel with the vibration damping system
Natural frequency no. | 1 | 2 | 3 | 4 | 5 | 6 |
Solid wheel natural frequency value, Hz | 1268 | 1836 | 2647 | 3110 | 3849 | 4510 |
Wheel w/vibration damping system natural frequency value, Hz | 1365 | 1857 | 2789 | 3378 | 3950 | 4535 |
Further laboratory tests performed on the test rig were intended to collect comparative data to enable a determination of the assumed vibration reduction ratios. The completed tests included various operating condition scenarios of the tested wheels: at maximum RPM under low, moderate and high loads (Table 5). The weight of a complete roller-coaster car without passengers is 5800 N and 9200 N with all possible passengers, and with the maximum excessive load resulting from movement on the track curvature equal to 1.8 g, the car will press on the track with a force equal to 16560 N. With 8 driving wheels on the car, the average load of a wheel in such conditions will be correspondingly 725 N, 1150 N and 2070 N. The weight of passengers and maximum excessive loads are relatively small, because the roller-coaster, for which the wheel is designed, is to be used by children and too high excessive loads would cause discomfort and reluctance to use the attraction again.
Fig. 10Natural vibration acceleration spectra for the solid wheel and the wheel with the vibration damping system in three directions perpendicular to one another: – solid wheel, – wheel w/vibration damping system
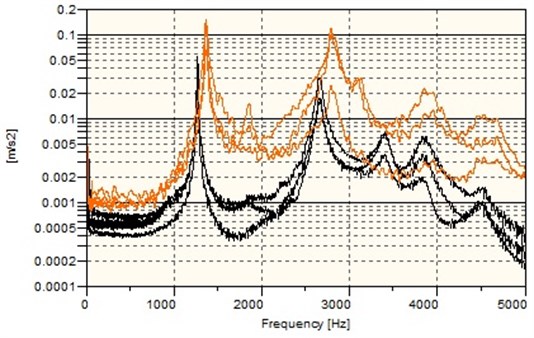
Table 5Wheel operating scenarios
Scenario | RPM | Load | Measurement | Analysis range | |
1 | Max. constant (190 rad/s) | Low | 725 N | Wheel bracket vibration | Vibration spectrum Total vibration level Effective vibration in freq. band 2-18 Hz Effective vibration in freq. band 18-2,000 Hz Effective vibration in freq. band 2,000-5,000 Hz Vibration reduction ratios |
2 | Moderate | 1150 N | |||
3 | Maximum | 2070 N | |||
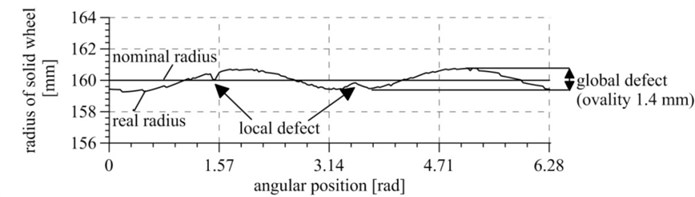
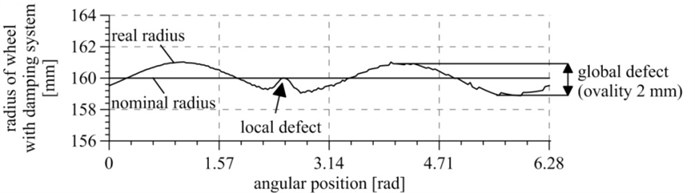
Measurements of the wheel radii tested showed wheel race defects. Fig. 11 presents measured radii of a solid wheel and wheel with vibration isolation system, in the angular position function. It appeared that wheel races show local concave and convex defects and global oval defects. Both kinds of defects will generate forces resulting in vibrations, and ovality will cause harmonic excitation of frequency overlapping the frequency of wheel turns (i.e. lower than 30 Hz). On the other hand, local defects will cause excitations close to pulse excitations, and each defect will generate one pulse per each wheel turn. According to the mechanical vibration theory, a pulse excitation excites all native frequencies of a system, i.e. causes high-frequency resonant vibrations of a wheel. On the other hand, an excitation caused by wheel ovality results in low-frequency vibrations. The analysis conducted shows that the excitation impacting the tested wheels is sufficiently complex to reflect actual operating conditions of the system.
The test results and completed analysis for every load scenario provided a determination of the acceleration spectrum and total vibration level in three perpendicular directions, in three predefined frequency bands. The acceleration signal recording time was 60 s; given the sampling frequency of 51200 Hz, this produced 46 Fourier transforms with a length of 216; the averaged spectra (at the averaging number of 46) were analysed.
Fig. 12 shows the vibration acceleration spectra for various directions at the maximum load on the wheel. This data suggests that the average maximum vibration amplitudes occurred in the medium frequency band, whereas the vibration levels of the wheel with the vibration damping system were lower than those for the solid wheel. The quantitative vibration reduction ratio in specific frequency bands for various load scenarios of the wheels was determined with the ratios defined by the relationships Eqs. (2) to (4). The results are shown in Tables 6 to 8.
Fig. 11Wheel race defects presented as wheel radius deviation from the nominal radius for various angular positions: a) for a solid wheel, b) for a wheel with a vibration isolation system
a)
b)
Fig. 12Vibration acceleration spectrum for various directions at the maximum load on the wheel: – solid wheel, – wheel w/vibration damping system
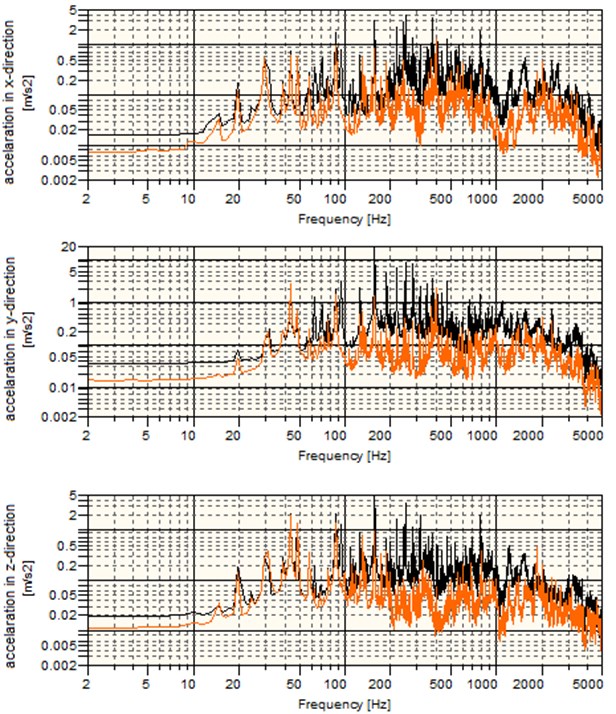
Tables 6 to 8 results show that the wheel with the vibration damping system can reduce vibration levels by an average of 36.63 % in the 2-18 Hz frequency band, 63.49 % in the 18-2000 Hz frequency band, and 44.96 % in the 2000-5000 Hz frequency band. Fig. 13 shows the total vibration levels representative of the total vibrations at all frequencies. In each tested load scenario of the solid wheel a very undesirable phenomenon was observed which manifested itself as a continuous increase in the total vibration level, which, under the low load, resulted in a rapid vibration level rise at about the 43rd second of the test. The observed phenomenon was caused by self-excited vibration. The wheel with the vibration damping system did not reveal a continuous increase in the total vibration level or self-excited vibration. The analysis suggested that the vibration levels were lower for the wheel with the vibration damping system than for the solid wheel.
Table 6Effective vibration reduction ratio values for low-frequency vibrations
Load | Direction | , m/s2 | , m/s2 | , % |
Low | X | 0,0148 | 0,0282 | 47,39 |
Y | 0,0127 | 0,0869 | 85,34 | |
Z | 0,0209 | 0,0268 | 21,98 | |
Moderate | X | 0,0187 | 0,0183 | –2,28 |
Y | 0,0184 | 0,0265 | 30,53 | |
Z | 0,0195 | 0,0259 | 24,62 | |
High | X | 0,0133 | 0,0222 | 40,25 |
Y | 0,0156 | 0,0361 | 56,64 | |
Z | 0,0163 | 0,0218 | 25,26 | |
Average effective vibration reduction ratio for low-frequency vibrations (2-18 Hz) (various loads and directions) | 36,63 | |||
Table 7Effective vibration reduction ratio values for medium-frequency vibrations
Load | Direction | , m/s2 | , m/s2 | , % |
Low | X | 0,1014 | 0,2999 | 66,16 |
Y | 0,1527 | 0,9049 | 83,12 | |
Z | 0,1049 | 0,3286 | 68,05 | |
Moderate | X | 0,0970 | 0,1775 | 45,33 |
Y | 0,1439 | 0,2952 | 51,25 | |
Z | 0,1040 | 0,1837 | 43,37 | |
High | X | 0,0829 | 0,2774 | 70,11 |
Y | 0,1320 | 0,6257 | 78,89 | |
Z | 0,0935 | 0,2683 | 65,13 | |
Average effective vibration reduction ratio for medium-frequency vibrations (18-2000 Hz) (various loads and directions) | 63,49 | |||
Table 8Effective vibration reduction ratio values for high-frequency vibrations
Load | Direction | , m/s2 | , m/s2 | , % |
Low | X | 0,0426 | 0,1784 | 76,09 |
Y | 0,0512 | 0,1891 | 72,89 | |
Z | 0,0249 | 0,0844 | 70,51 | |
Moderate | X | 0,0469 | 0,0332 | –41,09 |
Y | 0,0567 | 0,0954 | 40,57 | |
Z | 0,0268 | 0,0303 | 11,58 | |
High | X | 0,0433 | 0,1098 | 60,51 |
Y | 0,0441 | 0,1210 | 63,48 | |
Z | 0,0255 | 0,0512 | 50,17 | |
Average effective vibration reduction ratio for high-frequency vibrations (2000-5000 Hz) (various loads and directions) | 44,96 | |||
Fig. 13Vibration levels for various direction and load scenarios
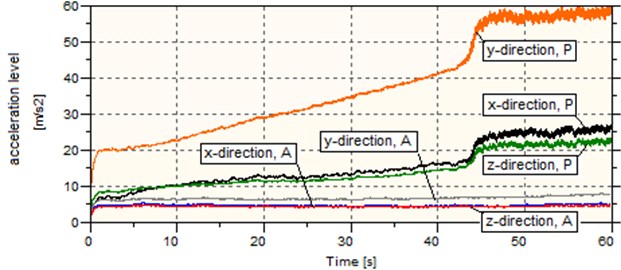
a) Minimum load
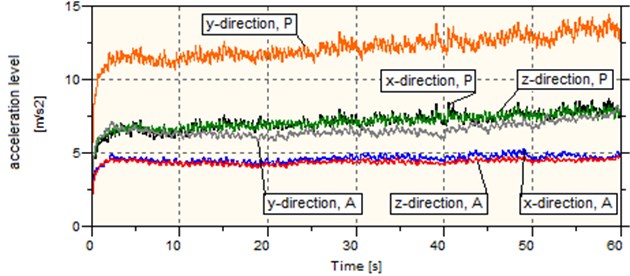
b) Medium load
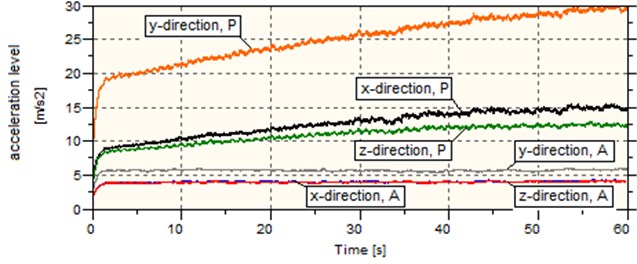
c)Maximum load
5. Conclusions
The completed tests and analyses led to the conclusion that the application of the wheel with the vibration damping system may:
– reduce vibration by an average of 36.63 % in the low frequency band (2-18 Hz);
– reduce vibration by an average of 63.49 % in the medium frequency band (18-2000 Hz);
– reduce vibration by an average of 44.96 % in the high frequency band (2000-5000 Hz).
Adopting a percentage-based assessment of vibration reduction is more favourable than determining vibration changes in absolute numbers. The vibrations that may occur in laboratory conditions vary in amplitude range when compared to actual vibrations under the normal operating conditions of the system; hence, it makes no practical sense to assess any vibration reduction expressed in absolute numbers. A viable conclusion in this case is that the percentage vibration reduction ratio demonstrated in laboratory conditions will occur in the normal operating conditions of a real system.
Moreover, the application of the system of resilient wheel webbing and the resilient insert provided a vibration damping effect, which reduced the total vibration levels and cancelled self-excited vibration.
Hence, a deliverable version of this experimental work was a prototype wheel with the vibration damping system that would be effective under actual operating conditions typical of roller coaster systems.
References
-
Weisenberger N. Coasters 101. An Engineer’s Guide to Roller Coaster Design, 2012.
-
Pendrill A. M. Rollercoaster loop shapes. Physics Education, Vol. 40, Issue 6, 2005, p. 517.
-
Pendrill A. M. Acceleration in one, two, and three dimensions in launched roller coasters. Physics Education, Vol. 43, Issue 5, 2008, p. 483.
-
Fujita K., Kimura T., Yamamoto Y. Motion and vibration analysis of a roller coaster. Proceedings of the Asme Design Engineering Technical Conferences, 2001.
-
Steišūnas S., Dižo J., Bureika G., Žuraulis V. Examination of vertical dynamics of passenger car with wheel flat considering suspension parameters. Procedia Engineering, Vol. 187, 2017, p. 235-241.
-
Verros G., Georgiou G., Natsiavas S. Multi-objective optimization of quarter-car models with linear or piecewise linear suspension dampers. ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2005, p. 2407-2415.
-
Pendrill A. M., Rödjegård H. A rollercoaster viewed through motion tracker data. Physics Education, Vol. 40, Issue 6, 2005, p. 522.
-
Shen Y., Chen L., Yang X., Shi D., Yang J. Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension. Journal of Sound and Vibration, Vol. 361, 2016, p. 148-158.
-
Ibrahim R. A. Recent advances in nonlinear passive vibration isolators. Journal of Sound and Vibration, Vol. 314, Issue 3, 2008, p. 371-452.
-
Merideno I., Nieto J., Gil-Negrete N., Ortiz J. G. G., Landaberea A., Iartza J. Theoretical prediction of the damping of a railway wheel with sandwich-type dampers. Journal of Sound and Vibration, Vol. 333, Issue 20, 2014, p. 4897-4911.
-
Šulc P., Pešek L., Bula V., Cibulka J., Boháč T., Tašek H. Pre-stressed rubber material constant estimation for resilient wheel application. Advances in Engineering Software, Vol. 113, 2017, p. 76-83.
-
Koradecka D., Koton J., Lipowczan A., Szopa J. Mechanical vibration. Central Institute for Labour Protection, Vol. 6, Issue 4, 2014, p. 1-10.
Cited by
About this article
Piotr Gierlak responsible for planning a measurement experiment, measuring and analyzing the system’s vibration. Dariusz Szybicki conducted numerical analyzes using the FEM. Krzysztof Kurc designed the roller coaster wheel in accordance with the patent application. Andrzej Burghardt responsible for designing and performing a test rig for dynamic tests of running wheel. Dawid Wydrzyński responsible for making wheel components according to the design. Radosław Sitek developed the design assumptions and analyzed the compatibility of the tested wheel with other roller-coaster components. Marek Goczał developed indicators for evaluating the researched system based on conducted environmental studies.
