Abstract
Condition monitoring and fault diagnosis via vibration signal processing play an important role to avoid serious accidents. Aiming at the complexity of multiple faults in a rotor-bearing system and drawback, the characteristic frequency of relevant fault could not be determined effectively with traditional method. The Spectral Kurtosis (SK) is useful for the bearing fault detection. Nevertheless, the simulation of experiment in this paper shows that the SK is unable to identify multi-fault of rotor-bearing system fully when different faults excite different resonance frequencies. A new multi-fault detection method based on EEMD and spectral kurtosis (SK) is proposed in order to overcoming the shortcoming. The proposed method is applied to multi-faults of rotor imbalance and faulty bearings. The superiority of the proposed method based on spectral kurtosis (SK) and EEMD is demonstrated in extracting fault characteristic information of rotating machinery.
1. Introduction
Rotating machinery is widely used for energy transformation and power transmission in industry. Rolling-element bearings are among the most common components of rotating machinery used for transformation of energy. The malfunctions of the bearing rotating system are mostly caused by the rotor and the bearing faults due to harsh operation conditions, which cause unexpected downtime and economic loss [1, 2]. Fault detection and diagnosis in rotor-bearing system based on vibration signal analysis is one of the principal tools [3]. The multi-fault diagnosis of rotor-bearing system is a difficult problem because the weaker fault signal is often buried in the other sources of vibration or background noise in the vibration signal [4, 5].
For condition monitoring of rotor bearing system, the vibration signals associated to damaged bearing typically produce an impulsive signature. In such case, the Spectral Kurtosis (SK) is useful by calculating Kurtosis value across different frequency bands [6]. The Spectral Kurtosis (SK) is developed by Dwyer [7]. Using the SK, it is possible to extract the part of the signal with the highest level of impulsiveness, enhancing the bearing fault signal from the raw data. The SK has been already applied successfully by many researchers in rotating machinery condition monitoring and fault diagnosis [8-10]. SK was directly applied to the bearing fault detection in induction motors in [8]. Professor Chu introduced the application of SK algorithm in the compound faults detection that happened in the gear and the rolling bearing of a gearbox simultaneously [9]. The kurtogram has now also been used for feature extraction of bearing in the presence of bearing faults [10].
Vibration signal of rotating machinery are facing to non-stationary characteristics when mechanical transmission system emerges fault. Empirical mode decomposition (EMD) has been proved an innovative and powerful approach for dealing with nonlinear and non-stationary signal [11]. Any complex information can be adaptively decomposed into a number of individual, nearly mono-component signals, named as intrinsic mode functions (IMFs). EMD has been introduced for the analysis of nonlinear and non-stationary signals of rotating machinery fault detection [12-14]. In order to solve the mode mixing problem that the EMD method may encounter, the ensemble EMD (EEMD) was proposed to improve the drawbacks [15]. EEMD is a noise-assisted data analysis method, and to restrain the mode mixing problem of EMD by adding white noise to the initial data. Admittedly, EEMD method is a great breakthrough in the development of EMD algorithm evidently [16, 17].
In this paper, we propose a new method with combining the advantages of EEMD and SK for rotor bearing system multi-fault diagnosis. It can solve the challenging task of rotor bearing system multi-fault information and extract the different fault value. The rest of this paper is organized as follows. Section 2 presents a brief description of SK technique and EEMD algorithm, as well as the procedure of multi-fault detection based on EEMD and SK. Section 3 shows the resulting benefits by means of experimental tests using the proposed method. The conclusion is given in the final section.
2. Theoretical background and proposed method
2.1. Spectra kurtosis calculation
Kurtosis is a statistical parameter, the fourth order cumulant of random variables. The value of kurtosis is normally used in detecting the degree of impulsiveness in fault bearings from vibration data. Kurtosis is defined as [18]:
where is the sampled time signal, is the sample index, is the number of samples, is sample mean. The bearing fault features in the vibration data are often buried by strong background noise. The value of Kurtosis from real domain may be unable to reflect the peak of the faulty signal.
The SK is defined as the Kurtosis in the spectral domain. It is devoted at finding the optimal frequency and bandwidth for recovering the demodulated impulsive signal that is mixed in the raw vibration waveform. The spectral kurtosis at each frequency can be obtained by Eq. (2):
where is the time-frequency averaging operator. and represents the fourth-order and the second-order cumulants respectively of signal at frequency point.
2.2. The definition of EEMD
To solve the problem of mode mixing, EEMD is introduced based on the statistical properties of white noise. The EEMD algorithm can be given as follows [15]:
(1) Given is an original signal, add a random white noise signal to :
where is the noise-added signal, 1, 2, 3,..., , and is the number of trials.
(2) Decompose into a series of intrinsic mode functions (IMFs) utilizing EMD as follows:
where denotes the ith IMF of the th trial, denotes the residue of th trial and is the IMFs number of the th trial.
(3) If , then repeat steps (3) and (4) with different white noise series each time.
(4) Calculate the ensemble means of corresponding IMFs of decompositions as the final result:
(5) ( 1, 2, 3, ..., ) is the ensemble mean of corresponding IMF of the decompositions.
2.3. Procedure of multi-fault detection based on EEMD and SK
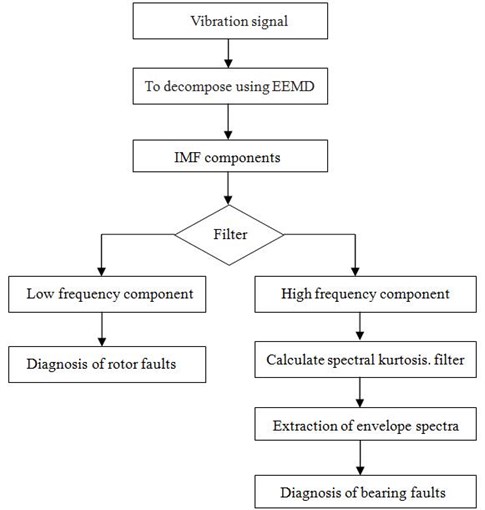
To impose a high demand for reliability on the feature extraction of the rotor bearing system running state, Application of EEMD analysis method can be used to decompose different frequency bands and eliminate the interference signal. For the low frequency components of EEMD decomposition, the rotor failure can be analysed directly. For the high frequency demodulation components of EEMD decomposition, the fault feature can be extracted combining with spectral kurtosis. Flow chart shown in Fig. 1, the specific diagnostic steps are as follows:
1) The fault vibration signal is decomposed by using EEMD method.
2) The low-frequency IMFs from decomposition is analysed in the spectrum, to show rotor unbalance failure characteristics.
3) The signal with faulty bearing impulsive feature is obtained from the decomposed high-frequency IMFs. Kurtogram and the corresponding envelope is calculated by spectral kurtosis. The bearing fault characteristic frequency is extracted from the envelope spectrum.
4) The proposed method is compared with SK by analyzing two different results of envelope spectrum. The diagnosis results show the advantages of this method.
Fig. 1Flow chart of the new method
3. Application to the fault diagnosis of rotating machinery
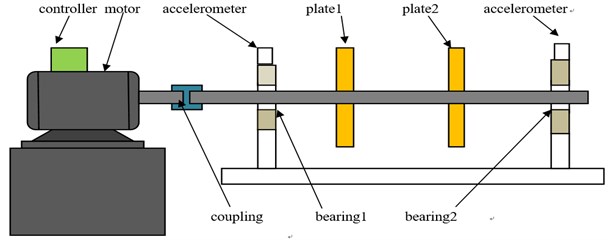
In this section, the proposed method is applied to the fault detection of multi-faults rotor bearing system. The rotor bearing system is the usual and key part for rotating machinery. The sketch and photograph of the rotor bearing system are shown in Fig. 2. The unit is composed of a shaft, a motor, two plates, coupling and bearings. The rotating speed is 1200 r/min (20 Hz). Vibration signals were taken from the radial direction of the No.2 bearing by acceleration sensor. Depending on whether the rotor system has a bearing fault, the sampling frequency is set to 2560 Hz and 5120 Hz, respectively.
Fig. 2The experiment setup of rotor bearing system
a)

b)
Four different faults including the normal, unbalance, bearing inner ring failure and imbalance-bearing inner ring coupling failure are simulated in the experiment. The vibration signals of the four different running states were collected by an acceleration transducer fixed on the bearing box, which are illustrated in Fig. 3. A series of fluctuant sine waveforms and some waveforms with pulse signals can be seen from Fig. 3.
The Fourier transform spectrum of the four different signals are shown in Fig. 4. The change of amplitude values and spectrum distribution can be seen with the four different signals.
3.1. Fault diagnosis of spectra kurtosis
Analysis only employing SK was undertaken on all data. The spectral kurtosis of normal signal and unbalance signal are shown in Fig. 5. It is not useful to analysis data without impulsive feature. For the data with bearing fault, the spectra kurtosis method is also directly applied. Their plots and defaults of the center frequencies are shown in Fig. 6(a) and Fig. 7(a). With the goal of analysing vibration signal of bearing fault, these frequencies were employed for envelop analysis in Fig. 6(b) and Fig. 7(b). Results from enveloped analysis are shown that the frequencies feature of bearing fault can be partly explained using SK.
Fig. 3The vibration signal of the tested bearing
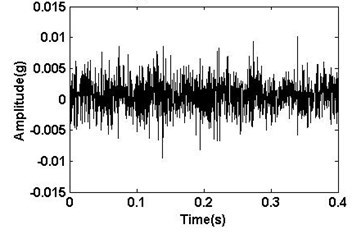
a) Normal
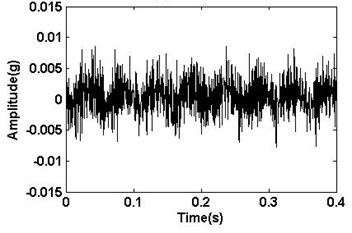
b) Unbalance
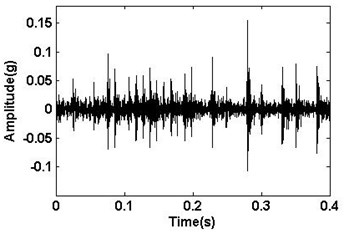
c) Inner race defect bearing
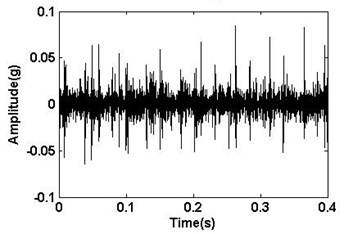
d) Unbalance and bearing inner race defect
Fig. 4The Fourier transform spectrum of the signal of Fig. 3
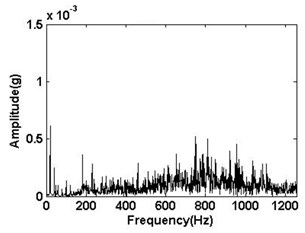
a) Normal
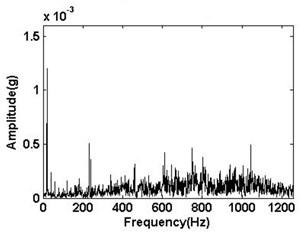
b) Unbalance
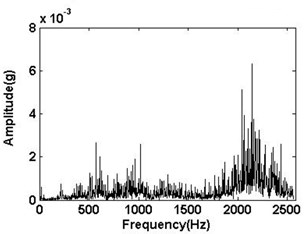
c) Inner race defect bearing
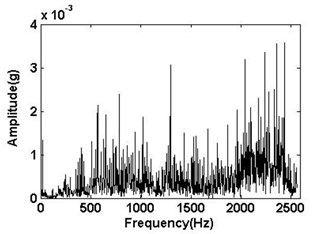
d) Unbalance and bearing inner race defect
3.2. Fault diagnosis of EEMD
In this section, the EEMD method was applied to the four different vibration signals of the tested bearing, which are shown in Fig. 3. They are respectively decomposed with the ensemble number of 100 and the white noise amplitude of 0.1 time standard deviation. After performing EEMD method on the four different vibration signals IMFs are obtained, as shown in Fig. 8. It could be seen that some local components of IMFs cover the most characteristic information. From Fig. 8(c) and Fig. 8(d), it can be found easily that the decomposed components IMF2 indicate the impulsive feature with bearing fault.
Fig. 5Spectrum kurtosis: a) normal, b) unbalance
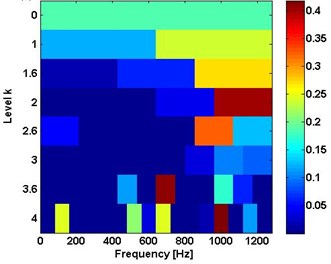
a)
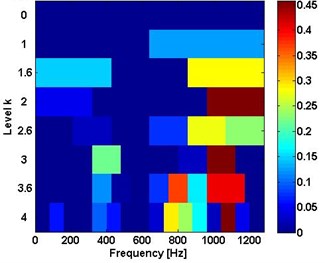
b)
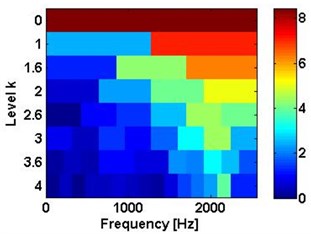
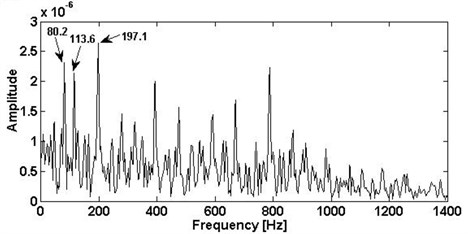
Fig. 6The results of inner ring fault: a) using SK, b) the corresponding envelope spectra
a)
b)
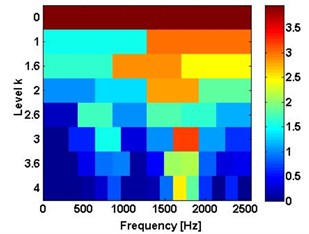
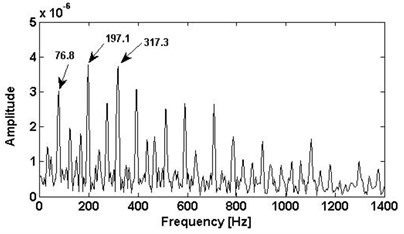
Fig. 7The results of unbalance and bearing inner race defect: a) using SK, b) the corresponding envelope spectra
a)
b)
The rotational frequency of the unbalance can be located in the lower frequency area of IMFs, which are presented in Fig. 8. We consider that the fault frequency value of the rotor unbalance is changed in the frequency spectrum. The frequency spectrum of the IMFs components with 20 Hz frequency are all performed and shown in Fig. 9. In the frequency spectrum, there is a predominant component and corresponding frequency is 20 Hz. Obviously, the amplitude of the rotating frequency 20 Hz will change when the rotating machinery is unbalance. For better comparison, the values of frequency 20 Hz are presented in the Table 1. Thus, the proposed method based on EEMD is able to effectively extract the unbalance features that are buried in the original vibration signal.
3.3. Fault diagnosis using the proposed method
The proposed algorithm is both applied to analyse the bearing inner race fault signal and compound faults signal (rotor unbalance fault and bearing inner race fault). The results of IMF2 in Fig. 8(c) and Fig. 8(d) are plotted in Fig. 10 and Fig. 11. With the algorithm proposed above, the spectral kurtosis is separately calculated and illustrated in Fig. 10(a) and Fig. 11(a). In the spectral kurtosis, higher SK values can be located. One of them is around 1900 Hz, and another can be found around 427 Hz.
Table 1Amplitude of Frequency 20 Hz
Signal | Frequency value (20 Hz) (×10-4) |
Normal signal | 5.154 |
Rotor unbalance signal | 8.287 |
Bearing inner race fault signal | 2.616 |
Multi-fault signal (unbalance and bearing inner race fault) | 6.494 |
Fig. 8The decomposed results of the vibration signals with EEMD
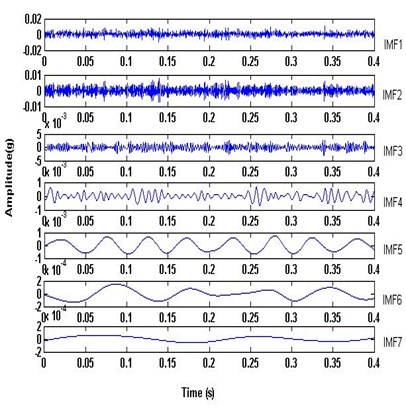
a) Normal signal
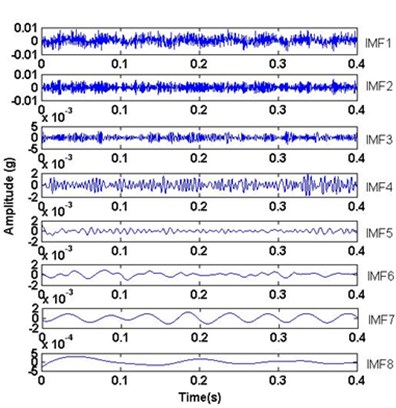
b) Unbalance signal
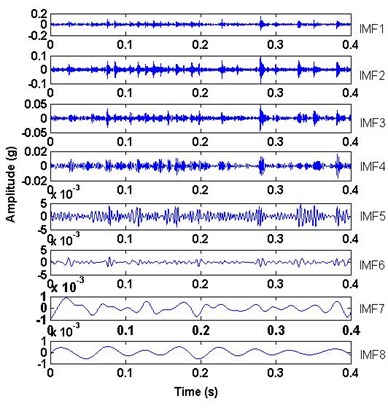
c) Bearing inner ring fault
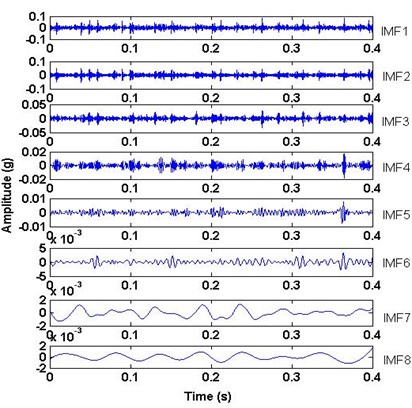
d) Unbalance and bearing inner ring fault
To provide the details of the bearing fault signal used above, the corresponding envelope spectrums of the filtered results of the bearing inner fault and the multi-faults are shown in the Fig. 10(b) and Fig. 11(b), respectively. The bearing inner race fault signal band is [1280 Hz, 2500 Hz] in level 1. The multi-fault signal band is [0 Hz, 854 Hz] in level 1.5. In Fig. 10(b) and Fig. 11(b), the bearing fault frequencies of the bearing inner race fault both can be located in the envelope spectrums. The prominent peaks can be easily found at 98.5 Hz, 197 Hz, 295.5 Hz and 395 Hz. They almost equal the theoretical results of bearing fault characteristic frequency and its harmonics.
The proposed method is also tested under the other two multi-faults as shown in Fig. 12 and Fig. 13, to get the bearing outer ring fault frequencies and rolling element defect frequencies. The results also equal the bearing fault theoretical characteristic frequencies. So, from the above fault detection it can be concluded that the proposed algorithm is able to detect multi-fault being in the rotor unbalance fault and bearing faults.
Fig. 9Frequency spectrum of IMFs with 20 Hz
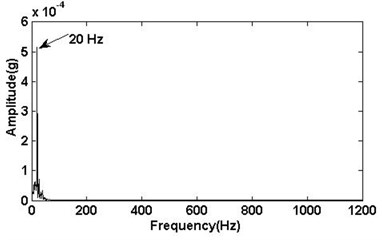
a) Normal
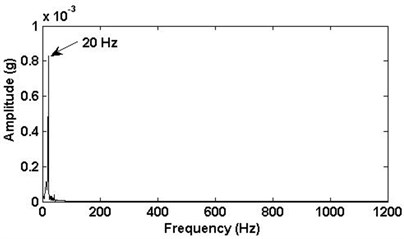
b) Unbalance
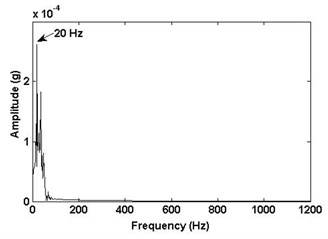
c) Bearing inner ring fault
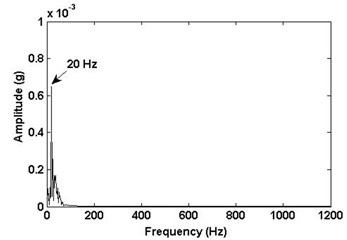
d) Unbalance and bearing inner race defect
Fig. 10The proposed method results of bearing inner ring fault
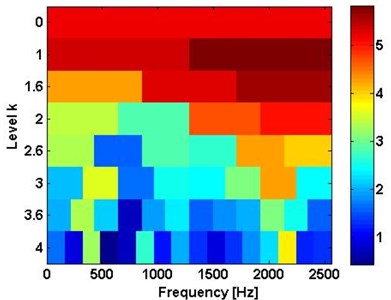
a) Kurtogram
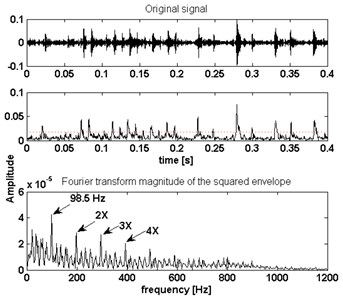
b) Envelope spectra
Fig. 11The proposed method results of unbalance and bearing inner race defect
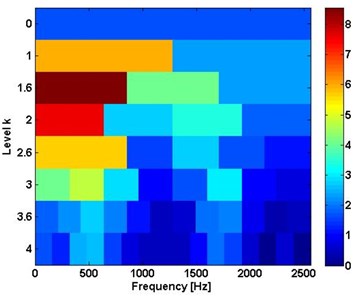
a) Kurtogram
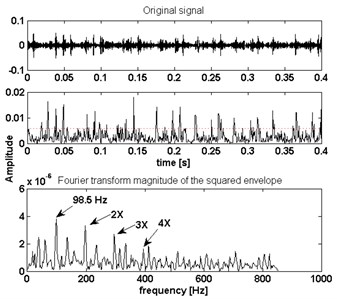
b) Envelope spectra
Fig. 12The proposed method results of unbalance and bearing outer race defect
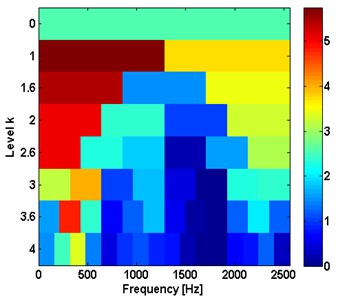
a) Kurtogram
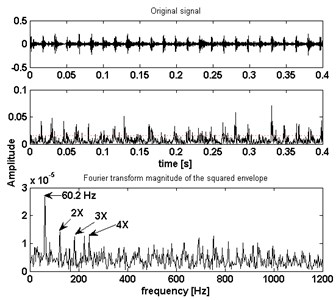
b) Envelope spectra
Fig. 13The proposed method results of unbalance and bearing rolling element defect
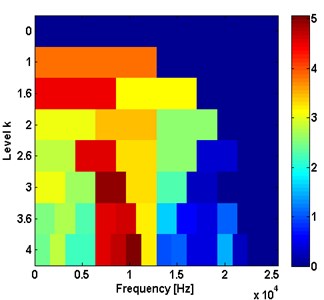
a) Kurtogram
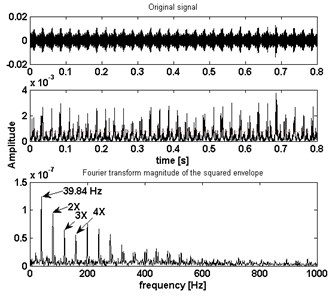
b) Envelope spectra
4. Conclusions
Spectral Kurtosis (SK) method is able to detect the bearing faults with impulsive signal. However, it is unable to fully reflect the fault characteristics in fault diagnosis of the multi-fault including imbalance and bearing faults. The ensemble empirical mode decomposition (EEMD) method provides a powerful tool for nonlinear signal analysis. It can decompose the complex signal into a number of intrinsic mode functions (IMFs). In this paper, we have proposed a new method on multi-fault signals, by means of EEMD and SK. The proposed method is applied to the diagnosis of the multi-fault in a rolling bearing and the unbalance of rotor system. The results show that the compound faults can be both detected by EEMD decomposing the raw signal, in which the imbalance signatures are buried in strong bearing fault frequency bands. Then SK is used for feature extraction of bearing inner ring fault, outer ring fault and rolling element fault from the modulated impulsive signal. The three envelope spectrums can finally indicate the presence of the bearing faults. This proves that the proposed algorithm is effective than only using SK algorithm.
References
-
Wang H., Gao J. J., Jiang Z. N., Zhang J. J. Rotating machinery fault diagnosis based on EEMD time-frequency energy and SOM neural network. Arabian Journal for Science and Engineering, Vol. 39, 2014, p. 5207-5217.
-
Miao Q., Wang D., Pecht M. A probabilistic description scheme for rotating machinery health evaluation. Journal of Mechanical Science and Technology, Vol. 24, 2010, p. 2421-2430.
-
Lal M., Riwari R. Multi-fault identification in simple rotor-bearing-coupling systems based on forced response measurements. Mechanism and Machine Theory, Vol. 51, 2012, p. 87-109.
-
Zhang D. C., Yu D. J. Multi-fault diagnosis of gearbox based on resonance-based signal sparse decomposition and comb filter. Measurement, Vol. 103, 2017, p. 361-369.
-
Liu Z. W., Wei G., Hu J. H., Ma W. S. A hybrid intelligent multi-fault detection method for rotating machinery based on RSGWPT. KPCA and Twin SCM, Vol. 66, 2017, p. 249-261.
-
Wang Y. X., Xiang J. W., Markert R., Liang M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mechanical Systems and Signal Processing, Vol. 66, Issue 67, 2016, p. 679-698.
-
Dwyer R. Detection of non-Gaussian signals by frequency domain kurtosis estimation. IEEE International Conference on Acoustics, Speech, and Signal Processing ICASSP’83, 8, p. 1983-607.
-
Vrabie V., Granjon P., Maroni C. S., Leprettre B. Application of spectral kurtosis to bearing fault detection in induction motors. Proceedings of the 5th International Conference on Acoustical and Vibratory Surveillance Methods and Diagnostic Techniques, Senlis, France, 2004.
-
Wang T. Y., Chu F. L., Han Q. K., Kong Y. Compound faults detection in gearbox via meshing resonance and spectral kurtosis methods. Journal of Sound and Vibration, Vol. 392, 2017, p. 367-381.
-
Lei Y. G., Lin J., He Z. J., et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mechanical System and Signal Process, Vol. 25, 2011, p. 1738-1749.
-
Huang N. E., Shen Z., Long S. R., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London, Vol. 454, 1998, p. 903-995.
-
Parey A., El Badaoui M., Guillet F., et al. Dynamic modeling of spur gear pair and application of empirical mode decomposition-based statistical analysis for early detection of localized tooth defect. Journal of Sound and Vibration, Vol. 294, 2006, p. 547-561.
-
Cheng J. S., Yu D. J., Tang J. S., et al. Local rub-impact fault diagnosis of the rotor systems based on EMD’. Mechanism and Machine Theory, Vol. 44, 2009, p. 784-791.
-
Rai V. K., Mohanty A. R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform. Mechanical Systems and Signal Processing, Vol. 21, 2007, p. 2607-2615.
-
Wu Z., Huang N. E. Ensemble Empirical Mode Decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, 2009, p. 1-41.
-
Zvokelj M., Zupan S., Prebil L. Non-linear multivariate and multiscale monitoring and signal denoising strategy using Kernal principal component analysis combined with ensemble empirical mode decomposition method. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 2631-2653.
-
Wang H. C., Chen J., Dong G. M. Feature extraction of rolling bearing’s early weak fault based on EEMD and tuneable Q-factor wavelet transform. Mechanical Systems and Signal Processing, Vol. 48, 2014, p. 103-119.
-
Saidi L., Ali J. B., Bechhoefer E., Benbouzid M. Wind turbine high-speed shaft bearings health prognosis through a spectral Kurtosis-derived indices and SVR. Applied Acoustics, Vol. 120, 2017, p. 1-8.
Cited by
About this article
This paper is supported by National Natural Science Foundation of China, (No. 51405453), by Program for Science and Technology Innovation Talents in Universities of Henan Province (No. 17HASTIT028) and by Key Scientific Research Projects of Henan Province (No. 16A460012).
