Abstract
Fault diagnosis of rotating machinery is of great significance in preventing catastrophic accidents and beneficially guaranteeing sufficient maintenance, which attracted a large number of researches to propose different diagnostic methods. However, different from the ideal state in laboratory, in practical engineering applications, the quality of collected vibration signals is vulnerable to environment and conditions and tends to be uneven, which lead to difficulties in accurate fault diagnosis. Concentrating on the signals with characteristics of poor quality, high noise and weak separability in the practical engineering applications, this paper proposes a CEEMD and ELM based fault diagnostic method. The proposed method contains four major steps: Row data acquired, feature extraction based on CEEMD and SVD, fault diagnosis based on ELM and calculation of total accuracy. At last, the proposed method is applied to a practical engineering application, fault diagnosis of a centrifugal pump. Results achieve a better fault recognition rate than the peer methods, which verifies the effectiveness and feasibility of the proposed method.
1. Introduction
Generally, rotating machinery under an abnormal state are accompanied with changes in vibration. Thus, the vibration analysis method has widely applied to diagnosis of the rotary machine fault diagnosis due to its intrinsic merits of revealing failure. It is generally accepted that vibration analysis method consists of three major aspects: (1) The acquisition of the fault vibration signals; (2) The extraction of fault features; (3) The state identification and fault pattern classification [1].
A lot of literature and researchers have developed a number of useful fault diagnosis method. In [2], a fault diagnosis method based on EMD-SVD and SVM is proposed by Cheng, which pays attention to the condition that the number of the samples is small. In [3], Da combined EMD with LS-SVM, and the simulation results show that the method can achieve a high accuracy. In [4], the authors focus on the improvement of the EMD method, and adopted LMD to gearbox for fault diagnosis. However, due to the sensitivity and confidentiality of collected data, most of the current methods are proposed to deal with data collected from an ideal condition in laboratory.
Different from the data acquired from laboratory, the signal acquired from practical engineering application has its own characteristics. Firstly, the mechanism of failure is totally different. In laboratory, signals are acquired in the way of fault injection, which leads to the fault features of the signal are obvious. While the mechanism of failure in practical engineering applications are derived from the real degradation of the product, which results in the difference between different fault modes in signals are small and difficult to recognize. Secondly, environment of signal acquisition has a significant effect on the quality of the signal. The laboratory environment is ideal, and the signal is almost not interfered by noise. However, in practical engineering applications the signal is always interfered by different kinds of noise. It means the practical signals are filled with plenty of noise and increases the difficulty of signal processing. Thirdly, fault coupling phenomenon occurs usually in practical applications, which means the fault of a product is actually the combination of some fault modes and one of them has the primary effect rather than a single fault mode.
For example, Fig. 1 shows the data comes from laboratory and practical engineering application. Signals of five fault modes are collected from a practical engineering centrifugal pump. Simultaneously, signals of four fault modes are collected from a bearing in lab environment for comparison. In Fig. 1, it is obvious to find that signals from the pump are full of noise and difficult to distinguish, while signals from the lab are so easy to classify that a glance is enough to recognize different fault modes.
All mentioned above makes the collected data from practical applications with characteristics of poor quality, high noise and weak separability, and contribute to the difficulty in implementing an effective and accurate fault diagnosis in practical applications.
Fig. 1Signals collected from practical engineering applications and laboratory environment
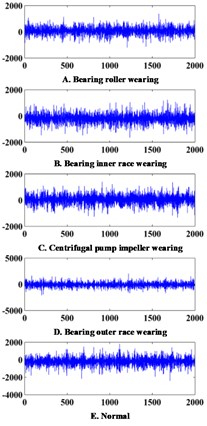
a) Signals collected from a practical engineering application: vibrational signals of a centrifugal pump
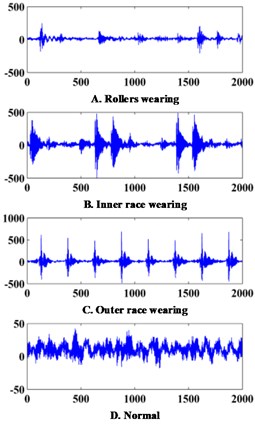
b) Signals collected from a laboratory environment: vibrational signals of a bearing
Empirical Mode Decomposition (EMD) proposed by Huang et al. is a commonly used method to process such nonlinear and non-stationary vibration signals of rotating machineries self-adaptively [5-7]. However, some obvious drawbacks exist in EMD such as over-envelopment, less-envelopment, mode confusion, high time consumption.
Ensemble EMD (EEMD), as an improved method of EMD, effectively inhibits the mode mixing phenomenon of EMD by adding Gaussian white noise sequence in the original signal [8]. However, EEMD is also incapable if the raw data have a low signal-to-noise ratio (SNR). The reconstructed signal still includes residual noise, and different realizations of signal and noise may produce different modes [9].
Complementary Ensemble Empirical Mode Decomposition (CEEMD) is similar to EEMD as it adds white noise to the input signals and uses the ensemble mean to extract the IMFs [8]. However, the more effective ensemble strategy makes CEEMD can not only overcomes mode mixing of EMD, but also avoid low computing efficiency of EEMD [10, 11]. And CEEMD is able to fully grasp the main features of the original signal. The most important thing is his strong anti-interference ability. Therefore, the CEEMD method is applied to decompose the vibration signals of different fault types.
The dimension of IMFs obtained from CEEMD is always too large and complex to be taken as the final fault features. To solve this problem and improve the robustness of the feature vectors, singular value decomposition (SVD) was introduced in this study to compress the scale of the fault feature vectors and obtain more stable feature vectors.
Naturally, after extracting fault feature vectors using CEEMD-SVD, the classifier is needed to automatically conduct the fault diagnosis. Extreme learning machine (ELM), as an intelligent technology, has shown good performance in regression applications as well as in large datasets and multi-label classification applications [12]. Moreover, ELM has been proven to require less human intervention and less running time than most other pattern recognition methods. In this study, ELM was introduced to accomplish the state classification. Therefore, aiming to practical engineering applications, a CEEMD and SVD based fault diagnostic method is proposed in this paper.
The subsequent paper is organized as follows: In Section 2, the framework of the proposed method is constructed and the fundamental principles of the CEEMD-SVD and ELM are reviewed briefly. In Section 3, the case study is performed to validate the proposed method. Finally, the conclusions and related future work are presented in Section 4.
2. Methodology
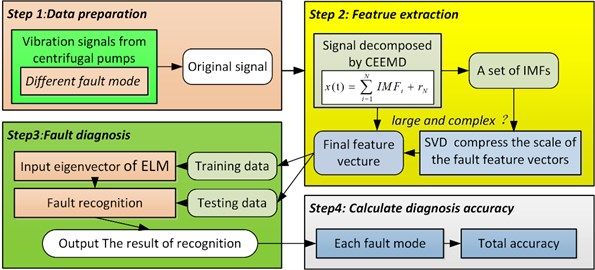
Fig. 2 shows the framework of the proposed method, which consists of four major steps: (1) Acquire the vibration signals under different fault modes. (2) CEEMD is applied to decompose sensor signals into several IMFs and then SVDs of each IMFs are extracted as signal features. (3) The feature vectors composed by CEEMD-SVD are input to the ELM for fault diagnosis. (4) Calculate the total accuracy.
Fig. 2Framework of the proposed method
Complementary ensemble empirical mode decomposition (CEEMD) is an improved algorithm based on empirical mode algorithm (EMD). EMD is an adaptive signal analysis method based on the signal characteristics of local extrema, which can have decomposed any non-stationary and nonlinear signals into intrinsic mode functions (IMFs) and a residue:
where denotes the number of IMFs decomposed by EMD under a given precision, represents the th IMF, is the residue after times decomposition [13] IMFs gained through EMD is distributed from high frequency to low frequency in frequency domain. As an improved method of EMD, the procedure of CEEMD can be describe as follows [14].
(1) Add white noise onto the initial signal and obtain the first EMD component of the data with noise. Repeat the decomposition and add different noise realizations and compute the ensemble average to define it as the first IMF1, that is:
Here, is the initial signal, is a radio coefficient, is the white noise realization while is the number of realizations. is an operator which returns the first IMF of the initial signal via decomposition with EMD [15].
(2) Calculate the first-order residual:
Then, see as the new signal and continue to decomposition until the signal meet the conditions of the first IMF, and define the ensemble average as the second IMF, denote it as :
(3) Repeat step (1) and step (2) until the th IMF component are obtained, that is:
Eq. (6) demonstrates that the initial signal was exactly reconstructed by CEEMD and the last step indicates the completeness of the decomposition method. Through the observation, we found that the first five IMF components contain the main feature information, so the first five IMFs are selected for further feature extraction.
ELM, proposed by Huang et al., was originally developed for single-hidden-layer feed forward neural networks and then extended to “generalized” single-hidden-layer feed forward networks (SLFNs). ELM is a novel learning algorithm with a faster learning speed and better generalization performance [16, 17]. The details of the ELM algorithm can be found in [18].
3. Case study
As shown in Fig. 3, data collected from the following centrifugal pump data acquisition system are used as the experimental raw data in our study and it comes from a practical engineering application. The signals are acquired from an installed accelerometer, with a sampling rate of 10.24 kHz.
In the experiment, data from five commonly occurring faults in the centrifugal pump are collected, namely normal, bearing roller wearing, bearing inner race wearing, bearing outer race wearing, and centrifugal pump impeller wearing.
Vibration signals of different fault modes are processed by CEEMD method, in which the radio of the standard deviation of the added noise is set to 0.15. A serious IMFs under different fault modes are obtained by CEEMD. The obtained IMFs are always too large to serve as the inputs of the classification method. To compensate this problem, SVD is introduced in this study. SVD is able to compress the scale of the decomposed components and the singular values have great stability. Therefore, they change little when the matrix elements change, which makes it possible to enhance the robustness of the proposed method under variable conditions.
The input eigenvector of ELM is extracted by CEEMD and SVD. Four set cross validations are adopted to verify the accuracy of the proposed method. For each fault mode, 160 sets of data are collected and the length of a data is 2000. Divide the 160 sets into 4 groups and each group is consisted of 40 data samples. Each group is selected as a training data set in turn, whereas the other 3 groups are selected as a test data set.
Table 1 presents a summary of the cross-validation results. From the diagnosis of ELM, we can conclude that all of the accuracy rates exceed 94 %. The cross- validation results of the four sets are 94.33 %, 94.00 %, 94.00 %, and 94.33 % respectively. Average classification accuracy is as high as 94.17 %, which verifies the effectiveness of the proposed method.
To further validate the superiority of the proposed method, the same data are used for the fault diagnosis with two peer methods. For comparison, (1) the fault diagnosis method based on EMD-ELM and (2) the fault diagnosis method based on CEEMD and PNN are chosen. Four sets cross validation is also adopted to the above methods. The results are also shown in the Fig. 4 and Table 2.
As shown in the Fig. 4 and Table 2, the proposed method achieves the accuracy of 94.17 % and the superiority of the approach is validated, by comparison with the EMD-ELM method and CEEMD-PNN method, of which the accuracy rates of classification are 90.94 % and 88.54 % respectively.
Fig. 3Centrifugal pump data acquisition system

Fig. 4Comparison results of diagnostic methods
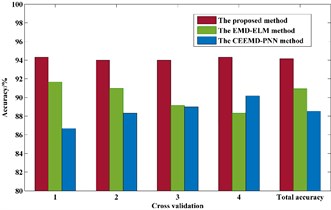
Table 1Results of 4 groups’ cross-validation
No. of group | Items | Fault modes | Total accuracy | ||||
A | B | C | D | E | |||
1 | Accuracy / % | 93.33 | 94.17 | 93.33 | 95.00 | 95.83 | 94.33 |
2 | Accuracy / % | 93.33 | 94.17 | 93.33 | 92.50 | 96.67 | 94.00 |
3 | Accuracy / % | 94.17 | 95.83 | 92.50 | 93.33 | 94.17 | 94.00 |
4 | Accuracy / % | 94.17 | 93.33 | 94.17 | 95.00 | 95.00 | 94.33 |
Total accuracy / % | 93.75 | 94.38 | 93.33 | 93.96 | 95.63 | 94.17 | |
Table 2Classification accuracy of three methods
Fault diagnosis method | The classification accuracy of each set of cross validation | Total accuracy | |||
1 | 2 | 3 | 4 | ||
The proposed method | 94.33 % | 94.00 % | 94.00 % | 94.33 % | 94.17 % |
The EMD-ELM method | 91.67 % | 90.99 % | 89.17 % | 88.33 % | 90.94 % |
The CEEMD-PNN method | 86.67 % | 88.33 % | 89.00 % | 90.17 % | 88.54 % |
4. Conclusions
In this paper, we present a fault diagnosis method concentrating on the vibration signal with the characteristic of poor quality, high noise, and weak separability in practical engineering applications. The method contains four major steps: firstly, acquire the vibration signal under different fault mode. Then, CEEMD is applied to decompose sensor signals into several IMFs and then the SVD of the IMFs are extracted as signal features; next, the feature vectors composed by CEEMD-SVD are input into the ELM for fault diagnosis. Finally, calculate the total accuracy.
In the case study, the proposed method is applied to the fault diagnosis of a practical centrifugal pump. The proposed method achieves an accuracy rate of 94.17 % and the compared methods only achieve the accuracy rates of 90.94 % and 88.54 %, which verified the effectiveness and superiority of the proposed method.
However, we only applied the proposed method to a centrifugal pump, more rotating machineries and more conditions should be taken into consideration for further study.
References
-
Wang Y., Lu C., Li L. F., Tian Y. A centrifugal pump fault diagnosis approach based on LCDApEn and PNN. Vibroengineering Procedia, Vol. 5, 2015, p. 169-174.
-
Cheng J., Yu D., Tang J., Yang Y. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery. Shock and Vibration, Vol. 16, 2013, p. 89-98.
-
Dai G. Rotating machinery fault diagnosis based on EMD-approximate entropy and LS-SVM. Advanced Intelligent Computing Theories and Applications – International Conference on Intelligent Computing, Changsha, China, 2010, p. 485-492.
-
Liu S., Pan H., Liu T. Gearbox fault diagnosis based on local mean decomposition (LMD) and radial basis function neural network (RBF). Machine Tool and Hydraulics, 2015.
-
Yang Y., YuDejie, Cheng J. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. Journal of Sound and Vibration, Vol. 294, 2006, p. 269-277.
-
Cheng J., Yu D., Yang Y. A fault diagnosis approach for roller bearings based on EMD method and AR model. Mechanical Systems and Signal Processing, Vol. 20, 2004, p. 350-362.
-
Yang Y., Yu D., Cheng J. Roller bearing fault diagnosis method based on EMD and neural network. Journal of Vibration and Shock, Vol. 294, Issues 1-2, 2006, p. 269-277.
-
Lei Y., Zuo M. J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs. Measurement Science and Technology, Vol. 20, Issue 12, 2009, p. 125701.
-
Mahgoun H., Bekka R. E., Felkaoui A. Gearbox fault diagnosis using ensemble empirical mode decomposition (EEMD) and residual signal. Mechanics and Industry, Vol. 13, 2012, p. 33-44.
-
Zhao L., Yu W., Yan R. Rolling bearing fault diagnosis based on CEEMD and time series modeling. Mathematical Problems in Engineering, Vol. 2014, 2014, p. 1-13.
-
Zhou T., Zhu X., Liu Y., Peng W. Rolling element bearings fault diagnosis based on CEEMD and SVM. Vibroengineering Procedia, Vol. 5, 2015, p. 199-204.
-
Huang G.-B., Ding X., Zhou H. Optimization method based extreme learning machine for classification. Neurocomputing, Vol. 74, 2010, p. 155-163.
-
Bian J., Wang P., Mei Q., Lei M. Fault detection of rolling bearings through vibration analysis via the hybrid CEEMD-EMD approach. Prognostics and System Health Management Conference, 2014, p. 245-250.
-
Torres M. E., Colominas M. A., Schlotthauer G., Flandrin P. A complete ensemble empirical mode decomposition with adaptive noise. IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic, 2011, p. 4144-4147.
-
Li J., Liu C., Zeng Z., Chen L. GPR signal denoising and target extraction with the CEEMD method. IEEE Geoscience and Remote Sensing Letters, Vol. 12, 2015, p. 1615-1619.
-
Huang G. B., Zhu Q. Y., Siew C. K. Extreme learning machine: a new learning scheme of feedforward neural networks. Proceedings of International Joint Conference on Neural Networks, Vol. 985, Issue 2, 2004, p. 990-982.
-
Huang G. B., Zhu Q. Y., Siew C. K. Extreme learning machine: theory and applications. Neurocomputing, Vol. 70, 2006, p. 489-501.
-
Huang G. B., Ding X., Zhou H. Optimization method based extreme learning machine for classification. Neurocomputing, Vol. 74, 2010, p. 155-163.
