Abstract
Fractional order control schemes are being actively investigated for various systems. Fractional order concept is incorporated in integral (I), proportional integral (PI), proportional derivative (PD) or proportional integral derivative (PID) controller to investigate the performance of different state variables of the system. These techniques are often used for the purpose of technology transfer but very scanty research has so far been conducted using state space approach. The current investigation is initiated to observe the effect of fractional order controller using state space approach for the system's performance while tracking the position and regulating the speed of a linear servo cart system. Integer order controller based on proportional derivative (PD) approach is also shown for comparison. Simulation responses are presented and analyzed, in this investigation. The superiority of state space approach based fractional order controller is shown in the results. The paper contains a literature review on several control techniques used to control position and speed of a servo-cart system. An over view of mathematical modeling of servo cart system and a description of a proposed fractional controller is presented in this paper. A brief description of integer order control scheme is also presented. Simulated results are compared and discussed for both fractional order controller and integer order controller at the end of this paper.
1. Introduction
Servomotor based linear cart system is a powerful tool for real world applications. It can reduce many men-hours through designing an automated actuating system in production lines. Basically, the servo cart system is an important key element to use in variety of processes. Depending upon the type of production plant, position and speed control of servo cart system can be of major importance. For this very purpose, several studies are performed to design position tracking and speed regulating scheme to achieve accurate tracking, robustness and increased efficiency [1]. Such as, a PI control technique is applied to improve set point tracking as described in [2]. In this investigation, a simple design is proposed to enhance the performance using dynamic weighting technique. To change the error of the process related variable, the weighting factor is produced through on-line. Feed forward, and feedback are jointly composed and proposed in a compound controller as explained in [3]. Other than the PI control technique, a fuzzy logic based PID controller is tested for servo cart position control [4]. Actually, the Fuzzy controller is implemented for a large target value. But the PID controller is applied when the values are close to the targeted value. This PID controller is tuned alone using different techniques. For instance, Luus-Jaakola Optimization technique based PID tuning process is accomplished for position and speed control of a DC servo motor [5]. Integral-Square-Error (ISE) based PID tuning is also performed for servo cart position and speed control [6]. However, this tuning was accomplished with the help of optimization technique. Servo cart position and speed controller are further designed based on sliding mode control, PD control and PI control techniques [7-10]. In fact, 90 % of industrial processes are equipped with this PID controller. Perfect parameter tuning is the main aspect of this type of control. A chaotic ant colony algorithm with the adaptive multi-strategies (CASOAMS) concept is implemented to animatedly tuning the constraints of PID controller for the purpose to justify the effectiveness of various physical systems [11]. The adaptive control idea is implemented in to genetic algorithm (GA) and colony optimization algorithm to propose an adaptive collaborative optimization technique (MGACACO) for solving complex real-world optimization problems [12].
A self-adaptive algorithm is introduced recently based on artificial bee colony (ABC) optimization technique [13]. It is claimed that the proposed ABC algorithm is better than other EAs techniques for various physical real-world problems. It is also crucial to minimize the boundary errors while controlling support vectors of some physical systems. Therefore, a v-support vector classification (ν-SVC) is proposed implementing a robust regularization path algorithm [14]. Further, the ν-SVC is modified to propose an effective incremental support vector ordinal regression (SVOR) algorithm [15, 16]. Multiple constraints based real world control problems are suitable to be handled with this algorithm while the quadratic formulations are readily available. A multi-scale local phase quantity (LPQ) and principal component analysis (PCA) is proposed to construct the feature vectors of a fingerprint liveness detection algorithm [17].
It can be mentioned that the above controllers are considered as integer order controllers in general. But currently the fractional order differentiation and integration becomes an innovative technique to implement in various branches of science and technology. Specially for the automation industry, designing a fractional order controller is an attractive tool for researchers. Therefore, it opens a wide door to re-investigate and reexamine all the former works conducted so far based on integer order calculus. It is already well known that the effectiveness of integer order controller can be enhanced with the help of fractional order differentiation and integration [18-20]. While the tuning process is concerned to obtain the most suitable gain parameter, the fractional order controllers are flexible enough in compare to that of integer order techniques. Although the parameter tuning of fractional controllers is a complex process, yet there are various effective tuning techniques introduced and published in several papers (see for example [21]).
Some other works are accomplished for modeling fractional order real-world systems using fractional-order operator. For example, an operator without a singular kernel is implemented for modelling a fractional order steady heat flow process which developed an analytical solution of dynamic equations [22, 23]. An integral transform operator is also designed and implemented on the heat-diffusion problem [24]. Another type of fractional operator with a variable order is developed using monotonic increasing function and justified the usefulness for transport process [25]. Again, non-differentiable elements based LC circuit is studied using local fractional calculus, and obtained results were compared with the relaxation oscillator (RO) circuit [26]. Besides, fractional calculus based improved adaptive particle swarm optimization(DOADAPO) algorithm is proposed to solve gate assignment problem of airport [27].
In this current investigation, the challenge is taken to design a fractional order linear controller to control the position and speed of a linear servo cart system. Now a day, the fractional order method is being used for technology transfer, but a little significant work has been done based on state space approach. Traditional state space approach described in [28] is suitable to be introduced in fractional order dynamics. The approach is presented under the name “augmented system approach” [29, 30]. The stabilization issue of commensurate fractional order systems is studied using system augmentation, and used in [31, 32]. Fractional order tuning is performed in several recent works [33-35]. Therefore, the current study introduced in this paper designs a state space based fractional order integral controller. The proposed control scheme is compared to an integer order controller, and simulation results are shown.
The remaining part of the paper is organized as follows: Fractional order controller is designed in the next Section. Section 3 is dedicated to system description of linear servo cart unit and its model. In Section 4, the proposed control scheme is simulated for the position tracking and speed regulating of a linear servo cart system. Simulation results with comparison over integer order controller are presented in the same Section as well. Finally, the discussion and conclusion are addressed in Section 5.
2. Design of fractional order controller
Integral action based state feedback control is a very useful technique for set-point tracking application [36, 37]. State space model for integer order control of an LTI system can be represented by:
where, , and are state vector, a control input, disturbance input and output variables, respectively. Further, is the plant dynamic matrix, is the control input vector, is disturbance matrix and is the output gain vector. The law of control with state feedback based integral action is expressed by:
where, is the augmented state vector and the output of integral operator is mentioned by . This integral operator is produced through an integral control as shown in Fig. 1. The figure shows a control scheme based on state feedback with integer integral action. This control scheme helps to improve the quality of system response in terms of the steady-state error. For the computation of feedback gain vector and , any suitable method, such as Ackermann's formula can be implemented.
Fig. 1Control scheme based on a state feedback with integer integral action
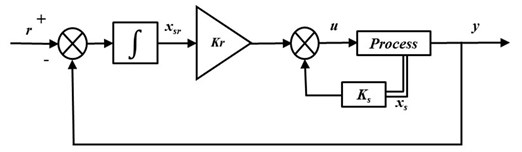
To implement fractional order control scheme, it is necessary to use fractional integrator 1/ instead of integer order integrator 1/ ( being a rational number between 0 and 1). Again, the static gain should be replaced by a compensator . Further, is used to stabilize the system. Fractional order integrator 1/is cascaded with compensator as shown in Fig. 2. The concept of Bode’s ideal transfer function [38] is the base to design this . The said transfer function is as follows:
where, and are responsible for the overshoot and the behavior of transient response for set point tracking. This Bode’s ideal transfer function helps to eliminate steady-state error in the response. It also guarantees the robustness of process gain and ensures the iso-damping property of step response for a closed loop system. These properties are not obtainable while using traditional state feedback control scheme with integer integral control action [33-35].
From the known overshoot, non-integer order can be calculated using the following equation which is referred from work of Barbosa et al. [39] and for more detail, one can see in [40, 41]:
Other way proposed in [38], can be implemented to calculate and from gain crossover frequency, and phase margin, . The required equations are as follows [29, 30]:
Fig. 2Fractional compensator based state space control [33-35]
![Fractional compensator based state space control [33-35]](https://static-01.extrica.com/articles/18519/18519-img2.jpg)
It can be noted that the structure provided in Fig. 2 is suitable for both stable and unstable system due to its state feedback, . It needs to design both integer filter and . Here the fractional integrator is cascaded by integer filter . Design steps are summarized in this paper, but the details are available in [35].
Now the law of control can be expressed for an LTI system as follows:
Let the above system is an integer order linear system. But to implement fractional action, a fractional derivative operator is introduced by the Eq. (8):
where, and are reference set-point and new states produced through fractional order integral (1/), respectively (order being a rational number between 0 and 1). The Fractional derivative operator is denoted by . is the output gain vector. is the gain vector need to be designed to place number of poles for the characteristic roots in the state feedback loop. Which can be stated in Eq. (9) and can be evaluated with the help of Ackermann's method [42]:
of Eq. (7) is the impulse response of , which is an integer compensator. It can be computed as follows [35]:
where, is the numerator of the transfer function of integer system described in Eq. (1), and is loop characteristic polynomial of the inner loop described by the system and the state feedback vector . Further, a low pass filter, is cascaded to make it effective. It can be mentioned here that the order of the fractional integrator operator is equal to the fractional order of the reference model of Eq. (3).
2.1. Stability analysis of fractional order controller
Stability of the control structure is suitably proved in [35] in which one can see the obtained Laplace transformed output equation as follows:
where, is essential to obtain the closed loop transfer model similar to Bode’s Ideal transfer function, stated in Eq. (3). Then the integer order filter is cascaded with the fractional integrator . These express the stability condition of the control scheme. Further, in [35], Eq. (33) shows that the disturbances are rejected by the proposed control structure.
3. Mathematical modeling of linear servo cart system
A linear servo cart system is shown in Fig. 3. The cart has the mass, , velocity, . The motor pinion of the cart is experienced by viscous damping force , which is combined with other damping terms and obtained an equivalent damping coefficient, . is the driving force generated by the servo motor. Therefore, Newton’s second law of motion is described as follows:
where:
Note that, is the efficiency of the gearbox, is gear ratio, is the efficiency of motor, is the motor torque constant, is back-emf constant, is the radius of motor pinion, and is the motor resistance. Motor inductance is considered very low; therefore, it is ignored.
Now the driving force:
Here is applied voltage, and is actuator gain, which is obtained as . Hence, the Eq. (11) expresses the complete dynamic behavior of cart velocity which is directly influenced by input voltage . Therefore, the transfer function is obtained as follow:
From this transfer function, the steady sate gain and time constant are expressed as and respectively. Hence, the plant transfer function for cart speed to applied voltage is:
In Eq. (11), the inertial force due to motor armature is ignored. If this force is considered, then there will be only changes in time constant parameter and steady-state gain will remain unchanged such that:
where equivalent inertia term:
An integrator (1/) can be cascaded with the speed transfer function to obtain the transfer function of voltage and cart position. The resulting transfer function becomes:
Fig. 3Typical linear servo cart system [43]
![Typical linear servo cart system [43]](https://static-01.extrica.com/articles/18519/18519-img3.jpg)
4. Simulation results
Model parameters of the plant is chosen such as actuator gain, 1.727 N-m/V, equivalent damping coefficient, 12.04 N-m-s/rad and equivalent mass in terms of armature inertia of motor, 0.7031 kg. Hence, the time constant, and steady state gain is depicted as 0.0584 s and 0.143 m/s/V, respectively. Now the state space model of linear servo cart system is as follows:
The purpose of the control is to track the set-point of linear servo cart position, and speed, . Transfer functions for cart position and speed corresponding to this model are:
and:
where, 0.143 and The method discussed in Section No. 2 is implemented to solve the set-point tracking problem of linear servo cart system.
Since represents 2nd order transfer function model, both roots are comprised to be a second order polynomial where 0.591 and 26.0 rad/s, which complies with the expected time-domain specifications to control the position of linear servo cart system. In which, pick time 0.15 s, percentage overshoot 10 % and steady state error, 0 are chosen. The state feedback is calculated for fulfilling these requirements such that:
Now the transfer function between input signal and cart position output of closed loop system is:
This transfer function shows corresponding poles at the denominator. Now it needs to find the characteristic polynomial of fractional controller. To obtain this, phase margin and gain crossover frequency are measured considering the open-loop transfer function related to . The measured values are used in Eq. (5) and Eq. (6) to obtain the parameters 1.8657 and 0.5 s of the characteristic polynomial to design the fractional controller. The fractional controller, is designed with the help of Eq. (10). It is expressed as:
Here, 1 because is second order. A suitable value of is chosen as 0.005 s for the time constant of the filter in Eq. (26).
To prove the superiority of the proposed technique, integer order controller based on modified proportional derivative (PD) method is demonstrated as shown in Fig. 4. A high-pass filter with negative velocity feedback is incorporated in this integer order control scheme. The strategy of integer order control scheme, to be compared, is considered similar to the structure shown in Eq. (27):
where and are proportional gain and negative velocity feedback gain, respectively. is the control input and is the position measured for linear servo cart system. With the help of characteristic equation for closed loop system and equating with the standard second order system, the gains and are calculated 275.49 V/m and 5.54 V-s/m, respectively.
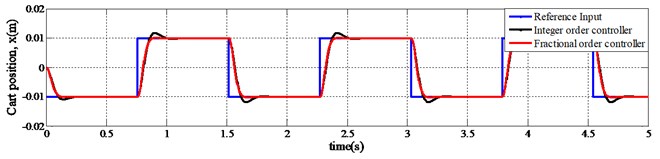
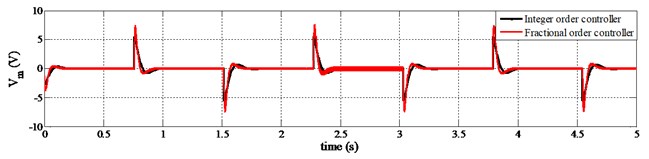
At first, the designed fractional order controller is evaluated and compared with integer order controller using simulation program for position tracking of a linear servo cart system. The position set-point of applied reference input changes such that, –0.01 m at 0 s and +0.01 m at 0.75 s. Square reference input signal is applied with one complete cycle time of 1.5 s. Fig. 5 represents the simulation results of position tracking performances for the linear servo cart system. The model used are described in Eq. (19) to Eq. (21). These results entail that, positions of linear servo cart are stabilized after some transient value, and then the cart tracks the set-point.
Although the duration of transient and steady state conditions is a fraction of a second, yet it is crucial for several complex applications like double or triple inverted pendulum, the inverted pendulum on seesaw, etc. A comparison is shown in this figure between integer order controller based PD compensator and fractional order controller. It is observed that the fractional order controller performed better than the integer order controller. Fig. 5 shows that; the position of the cart is disturbed using integer order controller when the set point is changing. But fractional order control laws provide no disturbance at all during the transition of set-point except some delay.
Fig. 4Block diagram of integer order control scheme
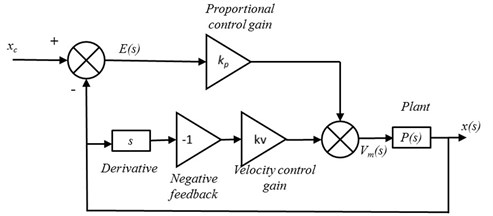
Fig. 5Position tracking control for a linear servo cart system
a)
b)
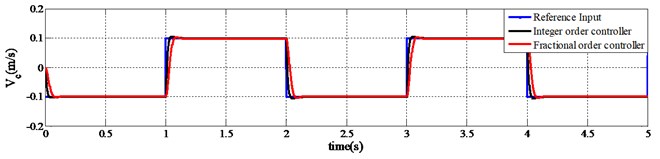
Further, the designed fractional order controller is evaluated and compared with integer order controller using simulation program for speed regulation of a linear servo cart system. The speed set-point of applied reference input changes such that, –0.1 m/s at 0 s and +0.1 m at 1.0 s. Step reference input signal is applied with one complete cycle time of 2.0 s. Fig. 6 represents the simulation results of the speed controller. It shows the performances of speed regulation of linear servo cart system. These results entail that, the speed of linear servo cart is perfectly following the set-point reference signal. A performance comparison is shown in the same figure between integer order controller and fractional order controller.
Fig. 6Speed tracking control for a linear servo cart system
a)
b)
It is observed that the fractional order controller performed well enough and almost similar to the integer order controller. Fig. 6 shows that, when the set point is changing, the speed of the cart is following the reference signal accordingly without any major overshoot except a slight delay.
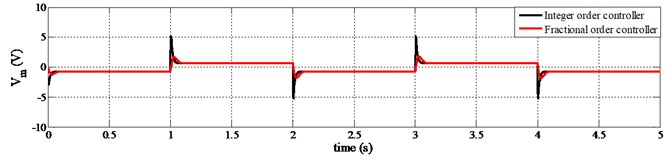
Again, in Fig. 5, the bottom one is showing the fluctuation of control voltage while the set-point changes. The amplitude of required control voltage is higher for fractional order control scheme than the integer one. However, the range of control voltage is still within the limit for both fractional and integer order controller. On the other hand, in Fig. 6, the amplitude of required control voltage for speed regulating of servo cart system is lower for fractional order control scheme than the integer one.
5. Conclusions
A fractional order controller is designed and simulated in this paper. Although, several research works are accomplished designing fractional order controller incorporating integral, proportional integral (PI), proportional derivative (PD) or proportional integral derivative (PID) controller to investigate the performance of different state variables of the system, but a little research is executed using state space approach to design fractional order controller. Therefore, the current investigation is conducted to observe the effect of fractional order controller using state space approach for the system’s performance in terms of position and speed tracking of a linear servo cart system. Linear servo cart system is a very powerful base unit to stabilize several highly unstable systems like double or triple inverted pendulum, double inverted pendulum with a flexible link, the inverted pendulum on seesaw, etc. Hence, the state space approach based fractional order controller is demonstrated here. Further, an integer order controller based on proportional derivative (PD) approach is also shown for comparison. Simulation responses are presented and analyzed. The comparative simulation results confirmed that the fractional order controller performed well then, the integer order controller while tracking the cart position and speed of a linear servo base system following a set-point reference input.
References
-
Huang M. S., Hsu Y. L., Fung R. F. Minimum-energy point-to-point trajectory planning for a motor-toggle servomechanism. IEEE/ASME Transaction of Mechatronic, Vol. 17, Issue 2, 2012, p. 337-344.
-
Pubali M., Chanchal D., Rajani K. M. An improved dynamic set point weighted pi controller for servo position control application. 2nd International Conference on Computational Intelligence and Networks (CINE), 2016, p. 145-149.
-
Ruijuan G., Yu H. The compound controller design of a position servo system based on the acceleration signal. 8th International Congress on Image and Signal Processing (CISP), 2015, p. 1489-1493.
-
Amanuel T., Ma J. Modeling and simulations on a fuzzy- PID position controller of electro hydraulic servo system. 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), 2015, p. 96-103.
-
Rathore N. S., Chauhan D. P. S., Singh V. P. Tuning of PID controller for position control of DC servo motor using Luus-Jaakola Optimization. International Conference on Computer, Communication and Control (IC4), 2015, p. 1-5.
-
Rathore N. S., Singh V. P., Chauhan D. P. S. ISE based PID controller tuning for position control of DC servo-motor using LJ. International Conference on Signal Processing, Computing and Control (ISPCC), 2015, p. 125-128.
-
Liu J., Er L. Sliding mode controller design for position and speed control of flight simulator servo system with large friction. Journal of Systems Engineering and Electronics, Vol. 14, Issue 3, 2003, p. 59-62.
-
Dharmana S., Chanchal D., Rajani K. M. An auto-tuning PD controller for DC servo position control system. 2nd International Conference on Power, Control and Embedded Systems, 2012, p. 1-6.
-
Luis F. C., Gustavo A. O. Design of a FPGA based position PI servo controller for a DC motor with dry friction. VII Southern Conference on Programmable Logic (SPL), 2011, p. 75-80.
-
Kherraz K., Hamerlain M., Achour N. Robust neuro-fuzzy sliding mode controller for a flexible robot manipulator. International Journal of Robotics and Automation, 2015, https://doi.org/10.2316/Journal.206.2015.1.206-3994.
-
Wu D., Huimin Z., Jingjing L., Xiaolin Y., Yuanyuan L., Lifeng Y., Chuanhua D. An improved CACO algorithm based on adaptive method and multi-variant strategies. Soft Computing, Vol. 19, Issue 3, 2015, p. 701-713.
-
Deng W., Zhao H., Zou L., Li G., Yang X., Wu D. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Computing, 2016, https://doi.org/10.1007/s00500-016-2071-8.
-
Xue Y., Jiang J. M., Zhao B. P., Ma T. H. A self-adaptive artificial bee colony algorithm based on global best for global optimization. Soft Computing, 2017, https://doi.org/10.1007/s00500-017-2547-1.
-
Bin G., Victor S. A robust regularization path algorithm for ν-support vector classification. IEEE Transactions on Neural Networks and Learning Systems, 2016, https://doi.org/10.1109/TNNLS.2016.2527796.
-
Bin G., Victor S., Keng Y. T., Walter R., S. L. Incremental support vector learning for ordinal regression. IEEE Transactions on Neural Networks and Learning Systems, Vol. 26, Issue 7, 2015, p. 1403-1416.
-
Bin G., Victor S., Zhijie W., Derek H., Said O., Shuo L. Incremental learning for ν-support vector regression. Neural Networks, Vol. 67, 2015, p. 140-150.
-
Chengsheng Y., Xingming S., Rui L. V. Fingerprint liveness detection based on multi-scale LPQ and PCA. China Communications, Vol. 13, Issues 7-2016, 2016, p. 60-65.
-
Oustaloup A. La Commande CRONE. Herme’s Edition, Paris, 1991.
-
Oustaloup A., Mathieu B. La Commande CRONE Du Scalaire Au Multivariable. Herm’es Editeur, Paris, 1999.
-
Poblubny I. Fractional-Order system and PIλDμ controllers. JIEEE Transactions on Automatic Control, Vol. 44, Issue 1, 1999, p. 208-214.
-
Das S., Saha Das S., Gupta A. On the selection of tuning methodology of FOPID controllers for the control of higher processes. ISA Transactions, Vol. 50, 2011, p. 376-388.
-
Yang, Srivastava, Machado T. A new fractional derivative without singular kernel – application to the modelling of the steady heat flow. Thermal Science, Vol. 20, Issue 2, 2016, p. 753-756.
-
Yang X. Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. Thermal Science, Vol. 21, Issue 3, 2016, p. 1161-1171.
-
Yang X. A new integral transform operator for solving the heat-diffusion problem. Applied Mathematics Letter, Vol. 64, 2017, p. 193-197.
-
Yang, Machado T. A new fractional operator of variable order: application in the description of anomalous diffusion. Physica A, Vol. 481, 2017, p. 276-283.
-
Yang X., Machado T., Cattani C., Gao F. On a fractal LC-electric circuit modeled by local fractional calculus. Communications in Nonlinear Science and Numerical Simulation, Vol. 47, 2017, p. 200-206.
-
Wu D., Huimin Z., Xinhua Y., Juxia X., Meng And Bo S. L. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Applied Soft Computing, 2017, https://doi.org/10.1016/j.asoc.2017.06.004.
-
Mehedi I. M. Full state-feedback solution for a flywheel based satellite energy and attitude control scheme. Journal of Vibroengineering, Vol. 19, Issue 5, 2017, p. 3522-3532.
-
Bettayeb M., Mansouri R. IMC-PID fractional-order-filter controllers design for integer order systems. ISA Transaction, Vol. 53, Issue 5, 2014, p. 1620-1628.
-
Bettayeb M., Mansouri R. Fractional IMC-PID-filter controllers design for non-integer order systems. Journal of Process Control, Vol. 24, Issue 4, 2014, p. 261-271.
-
Farges C., Moze M., Sabatier J. Pseudo-state feedback stabilization of commensurate fractional order systems. Proceedings of the 10th European Control Conference, Budapest, Hungary, August 2009, p. 23-26.
-
Farges C., Moze M., Sabatier J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica, Vol. 46, 2010, p. 1730-1734.
-
Bettayeb M., Boussalem C., Mansouri R., Al Saggaf U.-M. Stabilization of an inverted pendulum-cart system by fractional PI-state feedback. ISA Transactions, Vol. 53, 2014, p. 508-516.
-
Mansouri R., Bettayeb M., Boussalem C., Al Saggaf U.-M. Linear integer order system control by fractional pi-state feedback. Fractional calculus: History, theory and application, Nova Publishers, 2014.
-
Al Saggaf U.-M., Mehedi I. M., Mansouri R., Bettayeb State M. Feedback with fractional integral control design based on the bode’s ideal transfer function. International Journal of Systems Science, Vol. 47, Issue 1, 2016, p. 149-161.
-
Ogata K. Modern Control Engineering. Prentice-Hall, Englewood Cliffs, NJ, 1991.
-
Kuo B. C. Automatic Control Systems. Prentice-Hall, Englcwood Cliffs, NJ, 1991.
-
Bode H. W. Network Analysis and Feedback Amplifier Design. Van Nostrand, New York, 1945.
-
Barbosa R. S., Machado J. A. T., Ferreira I. M. Tuning of PID controllers based on Bode’s ideal transfer function. Nonlinear Dynamics, Vol. 38, 2004, p. 305-321.
-
Al Saggaf U., Mehedi I. M., Bettayeb M., Mansouri R. Fractional-order controller design for a heat flow process. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 230, Issue 7, 2016, p. 680-691.
-
Bettayeb M., Mansouri R., Al Saggaf U., Mehedi I. M. Smith predictor based fractional-order-filter pid controllers design for long time delay systems. Asian Journal of Control, Vol. 19, Issue 2, 2017, p. 587-598.
-
Dorf R. C., Bishop R. H. Modern Control Systems. 9th Edition, Prentice-Hall, 2001.
-
Quanser SRV02. User Manual, Quanser Inc, 2009.
Cited by
About this article
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under Grant No. (G-419-135-37). The author, therefore, acknowledge with thanks DSR for technical and financial support.
