Abstract
Aiming at the lack research of high-speed water-entry for large projectile, this paper studied the high-speed water-entry for hemispherical-nosed projectile in the method of fluid-solid coupling. Good agreements were obtained compared with the theoretical results. The modalities of water were calculated such as cavity, uplift and pressure. The velocity and deceleration curves of water-entry were gained. Numerical research shows that there is heavy shock pressure on the projectile and pressure waves in water by a projectile impacting into water at high speed, the pressure at the apex and the vicinity is much higher than the rest of area. The projectile’s peak acceleration is in linear correlation with the square of impact velocity. The simulation affords bases for impact-resistant design of the airdropped projectile, and of certain value to investigation of other correlative bodies’ high-speed water-entry.
1. Introduction
There will be a lot of phenomenon during high-speed water entry by a projectile, such as cavity, pressure wave and so on. For a long time, related research always concentrate on what have happened in water, rarely on the projectile itself. This paper is aimed to study the high-speed water-entry phenomena of hemispherical-nosed projectile.
Wang Jian investigated the phenomenon of the rocket sled water-brake high speed entering into water by using the method of fluid-solid coupling. The modalities of water were calculated such as super-cavitations, uplift, spatter and pressure, and the velocity, deceleration and resistance coefficient varied with time of water-brake was gained [1]. Song Baowei established the model of water-entry impact force for airdropped projectile based on the unsteady potential flow theory of incompressible liquid. And the simulation results show that the water entry impact force is huge, the maximum impact force is directly proportional to the square of water entry velocity [2]. High-speed water-entry should consider the water’s compressibility, which can be ignored at low-speed.
Investigations on the low-speed water-entry of large projectiles are relatively mature. Due to the limitation of experimental conditions, the high-speed water-entry hasn’t been investigated very well [3-5]. The method of Fluid solid coupling is used in this paper to investigate the high-speed water-entry of the hemispherical-nosed projectile, and the compressibility of the water was taken into consideration.
2. Mathematical models
High-speed water-entry is complex, which contains fluid, water and solid. ALE (Arbitrary Lagrangian Eulerian) method is good at investigated it numerically.
ALE includes mass, momentum and energy conservation equations. The energy conservation equation can be ignored in subsonic conditions, and the rest equations are as follows [1]:
where is the fluid density, is the fluid velocity, is the hydrodynamic viscosity coefficient. is the convection velocity, is the stress strain, is the body force.
The eight node hexahedron element is used in the model, in which the fluid grids are defined as ALE and the solid grids are defined as Lagrangian. Cause of the symmetry of the model, the water-entry model can be simplified as a quarter models in order to reduce the work of computation. The numerical simulation model is as illustrated in Fig. 1.
Fig. 1Model of calculation domain
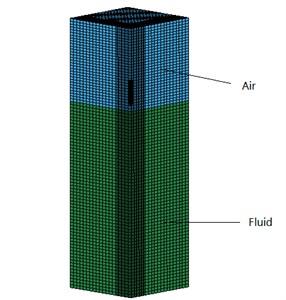
The projectile was in the air at the initial time. The profiles are defined as symmetry planes and the rest of surfaces are defined as none-reflect boundaries in order to simulate the unlimited-surroundings. Using level set method to track the interface of water and air and using operator splitting method to solve the fluid solid coupling equations.
The material of the water is null as well as the air. The water’s EOS is Gruneisen, and the air’s EOS is linear-polynomial. The material of the solid is common structural steel with hollow, and the average density of the projectile is 4000 kg per cubic meter.
3. Numerical validation
M. Lee considered a projectile with an impact velocity penetrating into a fluid along a straight trajectory in the direction. For normal penetration, the deceleration from the impact velocity can be described [6]:
where is the projectile mass, is the penetration velocity of the projectile, is the water density, is the projected area of the projectile, is a velocity-dependent drag coefficient, and is gravitational acceleration. For the high-speed water entry, the gravitational acceleration can be ignored, then the acceleration, , can be expressed as bellow:
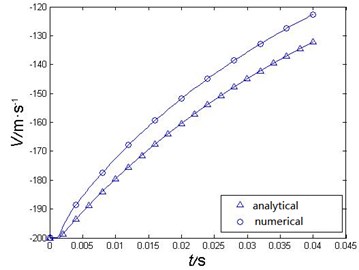
This paper simulated the water-entry of the hemispherical-nosed projectile with an impact velocity of 200 m/s based on the Eq. (3), and compared it with the numerical simulation results. The comparison is as Fig. 2.
The comparison certificates that the numerical simulation results are in good agreement with the calculated results. The numerical simulation results indicate that the acceleration in the impact stage is relatively fast, which is in consistent with the actual situation. So, ALE method can be used to investigate high-speed water-entry of hemispherical-nosed projectile.
Fig. 2A comparison of the velocity curve
4. Cavity of water entry
During high-speed water entry by a projectile, the kinetic energy loss equal the total energy stored in the fluid. Projectiles with different shapes have different cavities for that they have different velocity-dependent drag coefficients. The cavity formed during water-entry for hemispherical-nosed projectile is as Fig. 3.
After entering water, the projectile will squeeze water on both sides, and the surface water is uplifted. A spindly huge cavity of projectile nose shape will formed.
Fig. 3Cross section of the cavity
5. Projectile’s movement parameters
During the early water-entry, the projectile’s velocity descends rapidly. This paper analyzed the first 40 ms after the water-entry of a projectile with a impact velocity of 200 m/s. The velocity curve and the acceleration curve are as Figs. 4-5.
The projectile touched the water in 1.5 ms, and its acceleration reached the maximum in 2.0 ms. The maximum acceleration is about 5359 m/s2. The projectile’s acceleration decreases rapidly, and become gently in 3.6 ms, then the acceleration decreases relative slowly.
This paper also numerically simulated the maximum acceleration during water-entry of projectile with an impact velocity of 230 m/s and 260 m/s. Take a dimensionless coefficient of , which can be expressed as:
where is the impact velocity, is the peak acceleration. Then the comparison of the peak acceleration under different impact velocity is as Table 1.
Fig. 4Projectile’s velocity curve
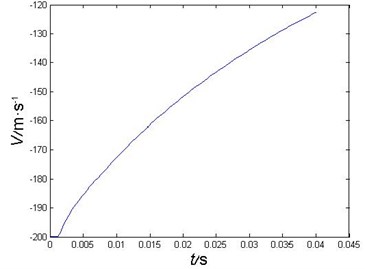
Fig. 5Projectile’s acceleration curve
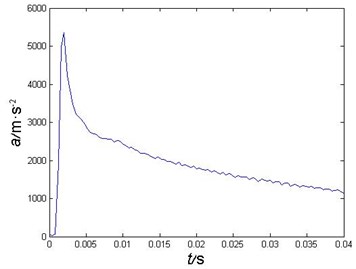
Table 1A comparison of the maximum acceleration under different impact velocity
Impact velocity (m/s) | 200 | 230 | 260 |
Peak acceleration (103m/s2) | 5.4 | 7.6 | 9.5 |
0.135 | 0.144 | 0.140 |
The comparison shows that the maximum acceleration of the projectile is in linear correlation with the square of impact velocity. Then a little raise in impact velocity will cause the maximum acceleration increases rapidly, especially for the range of the high-speed.
6. Pressures
The maximum pressure is a result of multiple effects of impact velocity, hydroelastic and nose-shape of the projectile. The contours of pressure around the projectile’s nose in 0.0016 s are as Fig. 6.
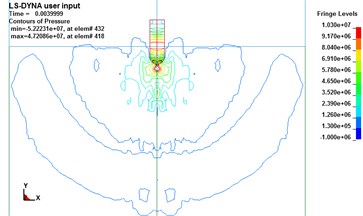
The compressed water expands again and releasing the compression energy in the form of pressure waves. The contours of pressure in 0.004 s are as Fig. 7.
Fig. 6Contours of pressures in 0.0016s
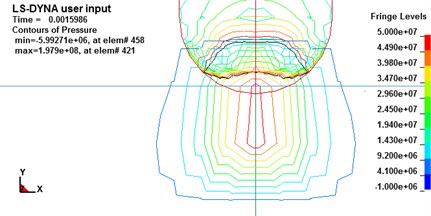
Fig. 7Pressure waves induced by water-entry
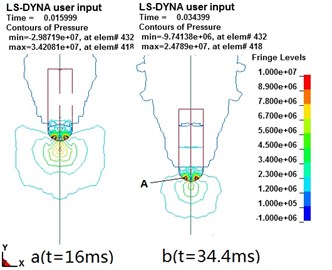
Pressure distribution on the nose is an important basis for the strength design of the projectile. During the water-entry, the pressures distributed on the nose of the projectile are as Fig. 8.
By observing the contours of pressure on the nose of the projectile, a conclusion can be found that the maximum pressure is not always at the apex of the projectile, at it will spread from the center to the periphery periodically, and there exists a relatively high pressure area near the apex.
Fig. 8Contours of pressure
7. Conclusions
This article investigated the high-speed water-entry for hemispherical-nosed projectile by the method of fluid-solid coupling. Good agreements were obtained compared with the analytical simulations. By numerically calculating the water-entry of the projectile with different impact velocity, this paper makes some conclusions as bellow:
1) There exists a huge maximum pressure for a short time on the projectile’s nose during the impacting.
2) The maximum acceleration is over 500 g for the hemispherical-nosed projectile when in an impact velocity of 200 m/s.
3) The maximum acceleration of the projectile is in linear correlation with the impact velocity.
4) For the water-entry of a hemispherical-nosed projectile, the maximum pressure is not always at the apex, it is spread from the center to the periphery periodically, but there exists a relatively high pressure area near the apex.
References
-
Wang Jian, Zhao Qing-bin, Tao Gang, Wu Jun-ji Numerical simulation on rocket sled water-brake high-speed water-entry impact. Explosion and Shock Waves, Vol. 30, Issue 6, 2010, p. 628-632.
-
Song Bao-wei, Du Xiao-xu, Meng Rui, Li Jia-wang, Shao Cheng Numerical simulation of water-entry impact force for air-launched mine. Torpedo Technology, Vol. 16, Issue 3, 2008, p. 6-8.
-
Pan Guang, Wei Gang, Du Xiao-xu The design and simulation of water entry and underwater trajectory for airdropped mine. Fire Control and Command Control, Vol. 32, Issue 3, 2007, p. 85-93.
-
Pan Guang, Yang Kui Impact force encountered by water-entry airborne torpedo. Explosion and Shock Waves, Vol. 34, Issue 5, 2014, p. 521-526.
-
Zhang Yue-qing, Cai Wei-jun, Li Jian-chen, Wang Zhi-jie Application of a FEM/SPH coupling method to torpedo water entry. Torpedo Technology, Vol. 25, Issue 1, 2017, p. 1-6.
-
Lee M., Longoria R. G., Wilson D. E. Cavity dynamics in high-speed water entry. Physics of Fluid, Vol. 9, Issue 3, 1997, p. 540-550.
