Abstract
The problem of hydroelastic oscillations of three-layer beam interacting with viscous liquid layer is set up and analytically solved. The problem presents the equation system of a three-layer beam and Navier-Stokes equations. The following boundary conditions are chosen: the no-slip conditions, the conditions for pressure at the edges, the simply supported edges conditions. The problem is solved for the steady-state harmonic regime. The frequency dependent distribution functions of the beam deflection are constructed. The given function allows investigating the resonance hydroelastic oscillations of a three-layer beam, as well as its deflected mode.
1. Introduction
The studies of elastic construction elements oscillation with consideration of their interaction with a liquid present an important issue of contemporary technology. For instance, the bending oscillations of a beam under interaction with an ideal incompressible liquid were considered in [1]. This solution made it possible to investigate the cylinder cavitations resource of the combustion engine with water cooling. The chaotic oscillations of the plate, interacting with an ideal incompressible liquid flow, are studied in [2]. Reference [3] is devoted to numerical study of rectangular plate hydroelasic oscillations, the plate being fully plunged into motionless ideal liquid or floating on its free surface. The analogous study for the case of rectangular plates interacting with the ideal liquid flow is made in [4]. However, the liquid viscosity is excluded from consideration in the above mentioned studies, but this property is very important, because it determines damping characteristics of oscillation system.
The study of vibrations of infinite length beam on viscous liquid layer was made in [5]. The study of hydroelastic oscillations of the elastic-fixed rigid wall of the finite sizes narrow channel is carried out in [6]. Hydroelastic oscillations of cantilever beam, plunged into a viscous incompressible liquid, are investigated in [7]. The problem of vibrating circular plates interacting with a layer of viscous incompressible liquid between them is solved in [8]. The analogous plane problem for the two vibrating plates of finite sizes is studied in [9]. Reference [10] investigates hydroelastic oscillations of the beam in a viscous liquid flow for the case of piezo-electric elements with the aim of obtaining energy from the flow. The problem of the bending hydroelastic oscillations of the plate under the impact of the viscous liquid pulsating layer was studied in [11]. The study of the hydroelastic oscillations of the plate, resting on Winkler foundation was made in [12-14].
References [15-18] consider the statics and dynamics of three-layer beams and plates under the local and distributed loads of various natures. The investigation of elastic three-layer plate dynamic interaction with a viscous liquid layer is of theoretical importance, while its results are of practical interest for computing and analyzing the new technology objects. But there is a shortage of studies devoted to the interaction of three-layer beams and plates with viscous liquid. For instance, the forced hydroelastic oscillations of the three-layered circular plate, interacting with viscous incompressible liquid layer under the channel foundation vibration, are investigated in [19]. Alongside with this, the hydroelastic oscillations of three-layer beam are of theoretical and practical interest, too.
2. Statement of the problem
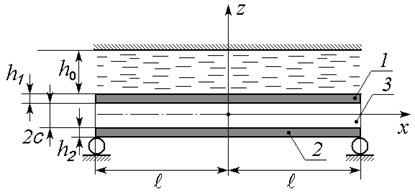
Let us consider the three-layer beam interacting with viscous incompressible liquid layer in conditions of foundation vibration (Fig. 1). We will study the plane hydroelastic problem. The foundation vibration takes place only in a vertical plane. The three-layer beam length is considerably larger than its width 2. The liquid pressure at the right and left edges is constant , and liquid leakage may be considered to be free. The liquid layer thickness is . The three-layer beam is the package consisting of bearing layers 1, 2, their thickness being and , and incompressible lightweight filler 3 with the thickness 2. The zig-zag hypothesis is valid for the three-layer beam, i.e. Kirchhoff hypothesis is valid for bearing layers, as well as the normal in the beam filler remains straight and turning by the angle [13-17]. Let us connect Cartesian coordinate with the center of beam filler medium surface in an undisturbed state. The rigid diaphragms, hindering the relative layers shift, but not impeding the deformation from its plane, are supposed to be situated at the beam edges [15-17]. Hence, the three-layer beam oscillations are caused by foundation vibration, while deformations of the plate are considered to be small. The three-layer beam is simply supported at its edges. Consideration of liquid viscosity leads to quick going down of transition processes, and according to [20], we can exclude the initial processes impact from the very beginning. That is why we will consider the steady-state harmonic oscillations.
Fig. 1A schematic diagram of the three-layer beam interacting with thin liquid layer
3. The theory
The law of foundation vibration motion will be presented in the form of:
Then acceleration of vibration foundation can be written as:
where is the amplitude of foundation oscillation, is the frequency, is the time.
The longitudinal waves are not studied, i.e. inertial forces in a longitudinal direction are not considered according to [21], while we study bending oscillations of the three-layer beam. In this case, dynamics equations of three-layer beam with incompressible lightweight filler will be written as [15]:
where is the shear modulus of th layer, is the bulk modulus of th layer, is the density of th layer material, 1, 2, 3 – layer number, is the longitudinal displacement of the beam, is the beam deflection, is the angle of rotation of the deformed normal in the beam incompressible lightweight filler, is the normal stress in the viscous liquid layer, is the shear stress in the viscous liquid layer.
The expressions for and take the form of [19, 22]:
The boundary conditions of Eq. (3) present simply supported edges conditions, i.e.:
The movement of thin viscous liquid layer can be considered as a creeping one [19]. Consequently, the dynamic equations of the liquid represent the Navier-Stokes equation without the inertia members, i.e. [22]:
where , are liquid velocity projections on the coordinate axis, is the density of the liquid, is the kinematic coefficient of the liquid viscosity, is the pressure.
The boundary conditions of Eq. (6) are the no-slip conditions and the ones for the pressure at the edges:
We introduce dimensionless variables and small parameters into the consideration of:
Taking into account Eq. (9), the Eqs. (6)-(8) in dimensionless variables in zero approximation on and will be written down, as:
Further, solving the problem of Eqs. (10, 11) we get:
The normal and shear stresses Eqs. (4), (5) in variables Eq. (9) take the form of:
According to the expressions Eqs. (14) and (15) the condition is made for a thin liquid layer. Thus, in comparison with normal stress, the shear one can be neglected, and by substituting Eq. (14) in Eq. (3) we get:
By using the first and the second equations (16), we find that:
Taking into account Eq. (18), we get from Eq. (17) the equation of a three-layer beam in the form of:
In view of the boundary conditions Eq. (6), we present the solution of the Eqs. (17), (18) in the form of:
Here is the harmonic time function, is the constant.
Bearing in mind Eqs. (13), (21) in the Eq. (19) and solving it we get:
where the symbols are introduced:
According to Eqs. (19), (20) and (17), we find the expressions for and :
where the symbols are introduced:
4. Summary and conclusion
The first component of Eqs. (22)-(24) corresponds to the loading from the constant pressure , while the second one corresponds to the impact of the channel vibrating foundation. The functions , , can be considered as the frequency dependent functions of deflection distribution, longitudinal displacement distribution and normal rotation angle distribution. The functions , , can be considered as the frequency dependent functions of phase response distribution of values, mentioned above. In the case of the specified value of the coordinate these functions transform into amplitude-frequency characteristics and phase response characteristics in the assigned cross section of the three-layer beam. On the basis of these functions analyses it is possible to investigate the three-layer beam hydroelastic oscillations under foundation vibration. Thus, the obtained mathematical model can be used for investigating the three-layer beam resonance oscillations, where the beam is a wall of a channel with viscous incompressible liquid inside, as well as for studying its mode of deformation under vibration.
References
-
Indeitsev D. A., Polypanov I. S., Sokolov S. K. Calculation of cavitation life-time of ship engine liner. Problemy Mashinostraeniya i Nadezhnos’ti Mashin, Vol. 4, 1994, p. 59-64.
-
Avramov K. V., Strel’nikova E. A. Chaotic oscillations of plates interacting on both sides with a fluid flow. International Applied Mechanics, Vol. 50, Issue 3, 2014, p. 303-309.
-
Kerboua Y., Lakis, Thomas A. A. M., Marcouiller L. Vibration analysis of rectangular plates coupled with fluid. Applied Mathematical Modelling, Vol. 32, Issue 12, 2008, p. 2570-2586.
-
Bochkarev S. A., Lekomtsev S. V., Matveenko V. P. Hydroelastic stability of a rectangular plate interacting with a layer of ideal flowing fluid. Fluid Dynamics, Vol. 51, Issue 6, 2016, p. 821-833.
-
Önsay T. Effects of layer thickness on the vibration response of a plate-fluid layer system. Journal of Sound and Vibration, Vol. 163, 1993, p. 231-259.
-
Ageev R. V., Mogilevich L. I., Popov V. S., Popova A. A., Kondratov D. V. Mathematical model of pulsating viscous liquid layer movement in a flat channel with elastically fixed wall. Applied Mathematical Sciences, Vol. 8, Issue 159, 2014, p. 7899-7908.
-
Faria Cassio T., Inman Daniel J. Modeling energy transport in a cantilevered Euler-Bernoulli beam actively vibrating in Newtonian fluid. Mechanical Systems and Signal Processing, Vol. 45, 2014, p. 317-329.
-
Mogilevich L. I., Popov V. S. Investigation of the interaction between a viscous incompressible fluid layer and walls of a channel formed by coaxial vibrating discs. Fluid Dynamics, Vol. 46, Issue 3, 2011, p. 375-388.
-
Mogilevich L. I., Popov V. S., Popova A. A. Dynamics of interaction of elastic elements of a vibrating machine with the compressed liquid layer lying between them. Journal of Machinery Manufacture and Reliability, Vol. 39, Issue 4, 2010, p. 322-331.
-
Akcabay D. T., Young Y. L. Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Physics of Fluids, Vol. 24, Issue 5, 2012.
-
Ageev R. V., Kuznetsova E. L., Kulikov N. I., Mogilevich L. I., Popov V. S. Mathematical model of movement of a pulsing layer of viscous liquid in the channel with an elastic wall. PNRPU Mechanics Bulletin, Vol. 3, 2014, p. 17-35.
-
Kuznetsova E. L., Mogilevich L. I., Popov V. S., Rabinsky L. N. Mathematical model of the plate on elastic foundation interacting with pulsating viscous liquid layer. Applied Mathematical Sciences, Vol. 10, Issue 23, 2016, p. 1101-1109.
-
Mogilevich L. I., Popov V. S., Popova A. A., Christoforova A. V. Mathematical modeling of hydroelastic walls oscillations of the channel on winkler foundation under vibrations. Vibroengineering Procedia, Vol. 8, 2016, p. 294-299.
-
Mogilevich L. I., Popov V. S., Popova A. A. Interaction dynamics of pulsating viscous liquid with the walls of the conduit on an elastic foundation. Journal of Machinery Manufacture and Reliability, Vol. 46, Issue 1, 2017, p. 12-19.
-
Gorshkov A. G., Starovoitov E. I., Yarovaya A. V. Mechanics of Layered Viscoelastoplastic Structural Elements. Moscow, Fizmatlit, 2005. (in Russian).
-
Kubenko V. D., Pleskachevskii Yu. M., Starovoitov E. I., Leonenko D. V. Natural vibration of a sandwich beam on an elastic foundation. International Applied Mechanics, Vol. 42, Issue 5, 2006, p. 541-547.
-
Starovoitov E. I., Leonenko D. V. Thermal impact on a circular sandwich plate on an elastic foundation. Mechanics of Solids, Vol. 47, Issue 1, 2012, p. 111-118.
-
Pradhan M., Dash P. R., Pradhan P. K. Static and dynamic stability analysis of an asymmetric sandwich beam resting on a variable Pasternak foundation subjected to thermal gradient. Meccanica, Vol. 51, Issue 3, 2016, p. 725-739.
-
Ageev R. V., Mogilevich L. I., Popov V. S. Vibrations of the walls of a slot channel with a viscous fluid formed by three-layer and solid disks. Journal of Machinery Manufacture and Reliability, Vol. 43, Issue 1, 2014, p. 1-8.
-
Panovko Y. G., Gubanova I. I. Stability and Oscillations of Elastic Systems. Consultants Bureau Enterprises, Inc., New York, 1965.
-
Vol’mir A. S. Shells in Fluid and Gas Flows: Aeroelasticity Problems. Nauka, Moscow, 1976, (in Russian).
-
Lamb H. Hydrodynamics, 6th Edition. Dover Publications Inc., New York, 1945.
Cited by
About this article
The study was funded by Russian Foundation for Basic Research (RFBR) according to the Projects Nos. 15-01-01604-a, 16-01-00175-a and President of Russian Federation Grant No. MD-6012.2016.8.
