Abstract
In the present work, a new equation to predict the maximum inter-story drift demands of mid-rise steel framed buildings is proposed in terms of a new ground motion intensity measures based on the spectral shape. For this aim, the maxim\um inter-story drift of steel frames with 4, 6, 8 and 10 stories subjected to several narrow-band ground motions is estimated as a function of the spectral acceleration at first mode of vibration , which is commonly used in earthquake engineering and seismology, and with a new parameter related to the structural response known as . It is observed that the spectral-shape-based intensity measure is the parameter best related with the structural response of the selected steel frames under narrow-band motions. For this reason, an equation to compute the maximum inter-story drift demand of mid-rise steel frames as a function of is proposed. The equation is useful for the rapid seismic assessment.
1. Introduction
The uncertainty of the structural response of buildings under several earthquake ground motions can be reduced if an efficient intensity measure (IM) is selected, where the efficiency is defined as the ability to predict the response of structures subjected to earthquakes with low uncertainty. Several studies have been developed with the aim to observe the relation between intensity measures and the seismic response of structures, and various intensity measures have been proposed [1-16]. Currently, several studies promote the use of vector-valued or scalar ground motion IMs based on spectral shape, because they predict with good accuracy the maximum inter-story drift and maximum ductility of structures subjected to earthquakes [8, 12-13]. In particular, vector and scalar ground motion intensity measures based on which are representative of the spectral shape have resulted very well related with the nonlinear structural response in terms of peak and energy demands [12-14, 17, 18]. Moreover, the parameter has been successfully used for ground motion record selection [19]. Nevertheless, most of the studies to illustrate the potential of -based intensity measures are related to the spectral shape in terms of acceleration were only the standard deviation of the maximum inter-story drift has been obtained, and it is necessary to estimate the relation between promising intensity measures and peak drift demands. In addition, it is important to establish equations to compute the structural demands in terms of ground motion intensity measures as Cornell and co-workers suggest [20]. For this reason, the first objective of the present paper is to compare the efficiency of the new ground motion intensity measure which is based on the spectral shape parameter in comparison with the most used intensity measure around the world which is the spectral acceleration at first mode of vibration. Then simplified expressions to compute the maximum inter-story drift demands of mid-rise steel framed buildings in terms of are proposed.
2. Methodology
2.1. Definition of the selected intensity measures
In the last years, the most used ground motion intensity measure by earthquake engineers, seismologists, and seismic design guidelines is the spectral acceleration at first mode of vibration. This parameter is very useful because is the perfect predictor of seismic response of elastic single degree of freedom systems and it is a good option for predicting the response of elastic multi degree of freedom structures dominated by the first mode of vibration. In addition, studies have demonstrated the sufficiency of with respect to magnitude and distance [7, 21]. Recently, various studies have demonstrated the inefficiency of , for example to predict the response of buildings under near source ground motion records and narrow-band motions [9, 12], energy demands [12, 22] and so on. The limitations of spectral acceleration at first mode of vibration can be clearly observed with the elastic response spectra where the scatter in the spectral shape due to the effect of the elongated period, or some spectral ordinates at higher mode periods is not considered. Inspired by this issues Bojórquez and Iervolino [12] have proposed the parameter and the intensity measure. Although these parameters have been described in works developed by the first author and co-workers, in the next section with the aim to better understanding the potential of and , they are defined.
2.2. The spectral shape parameter
Recent studies suggest that the spectral shape is crucial to predict the structural response of buildings under earthquakes and for this reason the earthquake engineering and seismology community has highlighted the limitations of spectral acceleration at first mode of vibration. For example, does not provide information about the spectral shape in other regions of the spectrum, which may be important for the nonlinear behavior (beyond ) or for structures dominated by higher modes (before ). In the case of nonlinear shaking, the structure may be sensitive to different spectral values associated to a range of periods defined, from the fundamental period and a limit value of practical interest, say . This calls for intensity measures providing information about the spectral shape in a whole region of the spectrum as and , where is defined as the ratio between the spectral acceleration at the period T2 divided by the spectral acceleration at period and is the geometrical mean between the period and . Although parameters as or the area under the spectrum, account for the spectral shape, a specific value of or area under the spectrum may be associated with different patterns of the spectrum between and , that is, with different spectral shapes. A useful improvement may be the use of normalized with respect to . To this aim the spectral shape parameter named Np (Eq. 1) was proposed by Bojórquez and Iervolino [12]:
2.3. ground motion intensity measure
To incorporate the effects of nonlinear behavior in the prediction of structural response, Bojórquez and Iervolino proposed a new scalar ground motion intensity measure based on and defined as:
In Eq. (2) the value has to be determined from regression analysis. Analyses developed by Bojórquez and Iervolino and others [12, 17] suggest that the optimal values of are close to 0.4.
2.4. Steel structures
Four steel frames having 4, 6, 8 and 10 stories were considered for the study. The frames are denoted as F4, F6, F8 and F10, and they were designed according to the Mexico City Seismic Design Provisions having three eight-meter bays and story heights of 3.5 meters. A36 steel was used for the beams and columns of the frames. For the dynamic analysis of the steel frames models, the RUAUMOKO program [23] was used. Relevant characteristics for each frame, such as the fundamental period of vibration (), and the seismic coefficient () are shown in Table 1 (the latter value was established from static nonlinear analyses). An elasto-plastic model with 3 % strain-hardening was used to represent the cyclic behavior of the transverse sections located at both ends of the steel beams and columns, and 3 % of critical damping was assigned to the first two modes of vibration of the frames.
Table 1Characteristics of the structural steel frame models
Frame | Number of stories | Period of vibration (s) | |
F4 | 4 | 0.90 | 0.45 |
F6 | 6 | 1.07 | 0.42 |
F8 | 8 | 1.20 | 0.38 |
F10 | 10 | 1.35 | 0.36 |
2.5. Earthquake ground motion records
A set of 30 narrow-banded ground motions recorded at Lake Zone sites of Mexico City was considered (see Fig. 1). All the motions were recorded at sites having soil periods near of two seconds, during seismic events with magnitudes near of seven or larger and having epicenters located at distances of 300 km or more from Mexico City. It should be mentioned that sites having soil periods of two seconds are fairly common within the Lake Zone and that the higher levels of shaking (in terms of peak ground acceleration PGA and velocity PGV) have been consistently observed at these sites. Moreover, most of the structural damages in the well-known 1985 Mexican earthquake occurred in the selected sites.
2.6. Incremental dynamic analysis
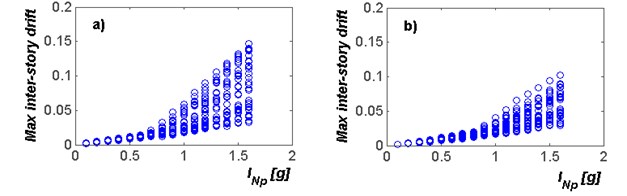
To observe the effectiveness of spectral acceleration and to predict the maximum inter-story drift demands of the selected steel frames under narrow-band motions, incremental dynamic analysis is used [24]. For this aim, the records are scaled at different spectral acceleration and values. Fig. 3 illustrate a typical plot of incremental dynamic analysis results for in terms of maximum inter-story drift demands calculated for frame models F4 and F6 under the selected narrow-band motions. It is observed a clear relation among and drift demands; however, the uncertainty to predict peaks demands using the spectral acceleration tend to increase if the level of intensity of the earthquake ground motion increases. For example for values smaller than 0.5 g, spectral acceleration is an excellent candidate as intensity measure since the uncertainty in the prediction is despicable, because the seismic response of the steel structure is almost linear elastic. Nevertheless, for values of intensities equals to 1.5 g, the maximum inter-story drifts are in the range of 0.02 up to 0.125, which indicate large uncertainty and the limitations of to predict the seismic response of this structure for large levels of nonlinear behavior. Thus, it is necessary to use new intensity measures with better prediction capacity of the structural response as in the case of as can be observed in Fig. 4. In this figure, incremental dynamic analysis for frames F4 and F6 is illustrated, where the horizontal axis corresponds to the records scaled at different values, and the vertical to the maximum inter-story drift. It is observed that for small intensity values, is an excellent predictor of the structural response. Moreover, for large values of intensities, the range of maximum inter-story drift demands at a specific level of is not so large as in the case of . For example, the range of peak drifts is from 0.05 until 0.1 for values of 1.6 g, indicating the advantages of using the new intensity measure in comparison with the spectral acceleration at first mode of vibration. The results suggest that large uncertainty is associated with the spectral acceleration as intensity measure. Thus, can characterize with better efficiency the seismic response of buildings under narrow-band motions, at least for the selected cases of the present study. This motivates the objective of the present study which is to propose simplified equations to compute maximum inter-story drift demands of steel frames as a function of . Note that this study corresponds to the firsts efforts related to scale records for a specific value.
Fig. 3Incremental dynamic analysis for the selected mid-rise steel frames under narrow-band motions using SaT1 as intensity measure: a) F4; b) F6
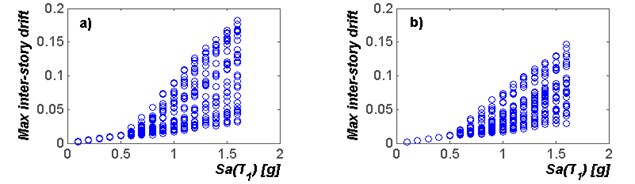
Fig. 4Incremental dynamic analysis for the selected mid-rise steel frames under narrow-band motions using INp as intensity measure: a) F4; b) F6
3. Equations to predict maximum inter-story drifts as a function of
In this part of the present study, a simplified equation to estimate maximum inter-story drift demands of steel frames under narrow-band ground motions is proposed. The equation has the form suggested by Cornell et al. [13], which is well-known as the power law model. This equation indicates that given the level of intensity (for example spectral acceleration), the predicted median inter-story drift demand can be represented as follows:
where is the median value of the maximum inter-story drift demand; is the selected intensity measure, in this study is used as intensity measure; and finally, and are parameters that must be calibrated in the regression. In general, the equations to obtain the median value of the maximum inter-story drift in terms of can be expressed as follows:
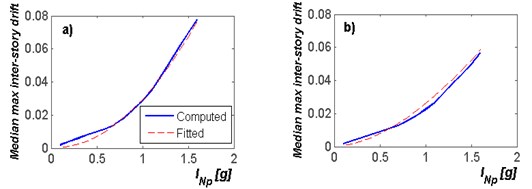
Fig. 5 shows the results of the fitted developed for the Frame F4 and F6 using as intensity measure. It is observed that the regression suggested a very well fitted with the median maximum inter-story drift values obtained from the incremental dynamic analyses. The values of and are expressed in terms of the ratio of structural period divided by the soil period (Eqs. (5-6)). Eqs. (5-6) are substituted in the above proposed simplified equation to predict the median maximum inter-story drift (Eq. (4)) as a function of the ground motion intensity measure (see Eq. (7)). It is important to say that the proposed equation is very useful for a rapid estimation of the structural response of buildings:
Fig. 5Median inter-story drift demands obtained from incremental dynamic analysis of the mid-rise steel frames in terms of INp for frames a) F4; b) F6
4. Conclusions
In this study, the efficiency of spectral acceleration at first mode of vibration to predict the seismic response of mid-rise steel framed buildings under narrow-band motions was compared with a recently proposed ground motion intensity measure accounting for nonlinear behavior, which is known as . It was observed the advantages of in comparison with , where the uncertainty to predict the maximum inter-story drift demands of the selected steel models was considerably reduced. Furthermore, a simplified equation to predict the median value of the maximum inter-story drift demands of mid-rise frames subjected to narrow-band ground motions in terms of has been proposed. Note that the equation is valid for steel framed buildings with structural vibration periods smaller than the soil period. The equations proposed are very useful for the rapid assessment of the structural damage, seismic fragility estimation, structural reliability, life cycle cost and so on.
References
-
Housner G. W. Spectrum intensities of strong motion earthquakes. Proceedings of the Symposium on Earthquake and Blast Effects on Structures. Earthquake Engineering Research Institute, 1952.
-
Housner G. W. Measures of severity of ground shaking. U.S. Conference on Earthquake Engineering. Earthquake Engineering Research Institute, 1975.
-
Arias A. A Measure of Earthquake Intensity. Seismic Design for Nuclear Power Plants. MIT Press, Cambridge, MA, 1970, p. 438-483.
-
Aptikaev F. F. On the correlations of MM Intensity with parameters of ground shaking. The 7th European Conference on Earthquake Engineering, Atenas, Grecia, 1982.
-
Von Thun J.L., Rochin L. H., Scott G. A., Wilson J. A. Earthquake ground motions for design and analysis of dams. Earthquake Engineering and Soil Dynamics: II. Recent advance in ground-motion evaluation, Geotechnical Special Publication, ASCE, New York, 1988, p. 463-481.
-
Cordova P. P., Dierlein G. G., Mehanny S. S. F., Cornell C. A. Development of a two-parameter seismic intensity measure and probabilistic assessment procedure. The 2nd U.S.-Japan Workshop on Performance-Based Earthquake Engineering Methodology for Reinforce Concrete Building Structures, Sapporo, Hokkaido, 2001, p. 187-206.
-
Shome N. Probabilistic Seismic Demand Analysis of Nonlinear Structures. Ph.D. Thesis, Stanford University, 1999.
-
Baker J. W., Cornell C. A. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthquake Engineering and Structural Dynamics, Vol. 34, 2005, p. 1193-1217.
-
Tothong P., Luco N. Probabilistic seismic demand analysis using advanced ground motion intensity measures. Earthquake Engineering and Structural Dynamics, Vol. 36, 2007, p. 1837-1860.
-
Riddell R. On ground motion intensity indices. Earthquake Spectra, Vol. 23, Issue 1, 2007, p. 147-173.
-
Mehanny S. S. F. A broad-range power-law form scalar-based seismic intensity measure. Engineering Structures, Vol. 31, 2009, p. 1354-1368.
-
Bojórquez E., Iervolino I. Spectral shape proxies and nonlinear structural response. Soil Dynamics and Earthquake Engineering, Vol. 31, Issue 7, 2011, p. 996-1008.
-
Bojórquez E., Iervolino I., Reyes-Salazar A., Ruiz S. E. Comparing vector-valued intensity measures for fragility analysis of steel frames in the case of narrow-band ground motions. Engineering Structures, Vol. 45, 2012, p. 472-480.
-
Minas S., Galasso C., Rossetto T. Preliminary investigation on selecting optimal intensity measures for simplified fragility analysis of mid-rise RC buildings. 2nd European Conference on Earthquake Engineering and Seismology (2ECEES), Istanbul, Turkey, 2014.
-
Kostinakis K., Athanatopoulou A., Morfidis K. Correlation between ground motion intensity measures and seismic damage of 3D R/C buildings. Engineering Structures, Vol. 82, 2015, p. 151-167.
-
Yakhchalian M., Ghodrati Amiri G., Nicknam A. Optimal vector-valued intensity measure for seismic collapse assessment of structures. Earthquake Engineering and Engineering Vibration, Vol. 14, 2015, p. 37-54.
-
Buratti N. A comparison of the performances of various ground-motion intensity measures. 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 2012.
-
Modica A., Stafford P. Vector fragility surfaces for reinforced concrete frames in Europe. Bulletin of Earthquake Engineering, Vol. 12, Issue 4, 2014, p. 1725-1753.
-
Bojórquez E., Reyes-Salazar A., Ruiz S. E., Bojórquez J. A new spectral shape-based record selection approach using Np and genetic algorithms. Mathematical Problems in Engineering, 2013.
-
Cornell C. A., Jalayer F., Hamburger R. O., Foutch D. A. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. Journal of Structural Engineering, Vol. 128, Issue 4, 2002, p. 526-533.
-
Iervolino I., Cornell C. A. Records selection for nonlinear seismic analysis of structures. Earthquake Spectra, Vol. 21, 2005, p. 685-713.
-
Bojórquez E., Astorga L., Reyes-Salazar A., Terán-Gilmore A., Velázquez J., Bojórquez J., Rivera L. Prediction of hysteretic energy demands in steel frames using vector-valued IMs. Steel and Composite Structures, Vol. 19, Issue 3, 2015, p. 697-711.
-
Carr A. RUAUMOKO Inelastic Dynamic Analysis Program. Department of Civil Engineering, University of Cantenbury, Nueva Zelanda, 2011.
-
Vamvatsikos D., Cornell C. A. Incremental dynamic analysis. Earthquake Engineering and Structural Dynamics, Vol. 31, Issue 3, 2002, p. 491-514.
About this article
The support given by El Consejo Nacional de Ciencia y Tecnología is appreciated. Financial support also was received from the Universidad Autónoma de Sinaloa under Grant PROFAPI.
