Abstract
Vibration signal modeling of a localized defective rolling bearing under unbalanced force excitations is carried out in this paper. A mass-spring-damping system with eight degrees of freedom is derived to consider the transverse vibrations and high frequency resonances of the rotor and bearing pedestals. External excitations come from the unbalanced mass and self-weight of the rotor. Due to the Hertz contact and bearing clearance, the dynamic model is coupled by the nonlinear stiffness. The inner/outer race defects are localized and modeled by additional contact deformations. The Runge-Kutta method is utilized to solve the nonlinear coupled differential equations and vibration signals with and without defects are obtained. Through envelope analysis, the fault characteristic frequencies of inner/outer raceway defects with and without unbalanced force excitations are presented. Detailed comparisons show that the unbalanced force excitations have significant influence on the fault characteristic frequencies. Finally, dynamic tests on a typical rotor-bearing system are conducted to verify the theoretical results.
1. Introduction
A lot of rotating machinery are supported by rolling element bearings. Due to manufacturing flaws or cyclic loading, localized defects frequently appear in bearing raceways. If undetected early, such defects can pose a potential source of catastrophic failures [1-3].
Thus, many researchers have therefore conducted extensive investigations on the dynamics of defected rolling bearings over the last decades. Patel et al. [4] developed a deep grooving ball bearing dynamics model that considers nonlinear contact force, investigated the dynamic characteristics when the inner and outer raceways contained single-point or multi-point local defects. Betea et al. [5] constructed a dynamics model of bearing systems with three degrees of freedom, which was employed to study the effect of inner and outer raceways defects on the dynamic characteristics of a system. Kankar et al. [6] established a high-speed bearing dynamics model that contains local defects on the inner and outer raceways. The established model considers nonlinear factors, such as the Hertz contact stiffness and the radial clearance. The characteristic frequencies of defects were successfully identified using the model and were verified using a test. Rafsanjania et al. [7] proposed an analytical model to study the nonlinear dynamic behavior of rolling element bearing systems including surface defects. Various surface defects due to local imperfections on raceways and rolling elements are introduced in the model. Using a six degrees of freedom dynamic model for deep groove and angular contact ball bearings, Ashtekar et al. [8] investigated the influence of race defects on the motions of bearing components (i.e. inner and outer races, cage, and balls).
In actual rotating machinery, some interaction factors, such as the meshing gear and induction motor rotor, might also have significant influences upon the vibrational response of the defective rolling bearing system. Sawalhi and Randall [9, 10] presented a combined dynamic model for gears and bearings, in which an extended fault in the inner/outer race of rolling element bearings was studied in the presence of gear interaction. Through detailed comparisons between the simulated and actual signals from the gear/bearing test rig for inner and outer race extended faults, they found a characteristic, referred to as double pulses, corresponding to entry into and exit from the localized fault. Immovilli et al. [11] proposed a novel bearing fault model for an induction motor, and the electromagnetic torque induced by air gap variations was considered as externally excitations. Both simulation and test results showed that the characteristic frequencies of bearing defects change due to the electromagnetic interaction. For the rolling element bearings used in the high speed spindle, dynamic modeling and vibration response simulation were conducted by Niu et al. [12] when localized surface defects occur in the raceways. Recently, the explicit dynamic finite element method was used to analyze the contact forces and vibration response of a defective rolling element bearing [13]. Various methods, such as empirical mode decomposition method [14], envelope analysis method [15] and singular spectrum method [16], were utilized for rolling element bearing fault diagnosis.
Besides the interactions of meshing gears and electromagnetic forces, the excitations induced by the unbalanced mass of rotor should also be considered in the dynamic modeling of defective rolling element bearings. For the vertical rotating machinery, the self-weight is along the axial direction and has no component in the two transversal directions. In the aero engine, the rotor’s gravity force is relatively smaller because of the widely used thin-walled rotating structures. In the two cases, the unbalance forces are the dominant load among the external loads. As the unbalance force rotates with the rotor and varies with time, so the load zone of the rolling bearing also varies with time. The contacts between the rolling ball and localized defects become more complicate due to the simultaneous rotations of both rolling balls and the load zone. Obviously, the fault characteristics of localized defects would have distinct differences with that of the weight-dominant condition, in which the load zone maintains constant.
Thus, dynamics of a localized defective rolling bearing is studied to show the difference between the weight-dominant and unbalance-force-dominant conditions. A mass-spring-damping system with eight degrees of freedom is derived to consider the transverse vibrations and high frequency resonances of the rotor and bearing pedestals. External excitations come from the unbalanced mass and self-weight of the rotor. Due to the Hertz contact and bearing clearance, the dynamic model is coupled by the nonlinear stiffness. The inner/outer race defects are localized and modeled by additional contact deformations. The Runge-Kutta method is utilized to solve the nonlinear coupled differential equations and vibration signals with and without defects are obtained. Through envelope analysis, the fault characteristic frequencies of inner/outer raceway defects are presented. Detailed comparisons are carried out to show the influence of unbalanced force excitations on the fault characteristic frequencies. Dynamic tests on a typical rotor-bearing system are conducted to verify the theoretical results. Finally, some conclusions are summarized.
2. Vibrational model for a rotor-bearing system
Fig. 1 gives a schematic diagram for a rotor supported by deep groove ball bearings. The inner raceway is connected to the rotor shaft and rotates under constant angular speed , while the outer raceway is fixed on the bearing pedestals. A mass-spring-damping system with eight degrees of freedom is derived to consider the transverse vibrations and high frequency resonances of the rotor and bearing pedestals. These degrees of freedom are described as follows:
1) Vibrations along two transversal directions and one axial direction for the rotor: , , and the mass and damping are denoted by , . The transversal supporting forces from the rolling bearings , ( 1, 2) will be derived based upon the Hertz contact theory in the following section. The axial support force from the rolling bearings is assumed to be linear and the support stiffness is denoted by .
2) Two bearing pedestals, respectively, have two transversal vibrations: , ( 1, 2). The lumped mass, support stiffness and damping are repressed by , , ( 1, 2). The coupling between the vibrations of rotor and bearing pedestals are realized through the nonlinear supporting forces , .
3) Moreover, the bearing pedestal would have high frequency resonance in working condition. Two mass-spring-damping systems with high resonant frequency are connected to the bearing pedestals [9]. The lumped mass, connection stiffness and damping are expressed by , , ( 1, 2).
Fig. 1Dynamic model for the rotor-bearing system with localized defective rolling bearing
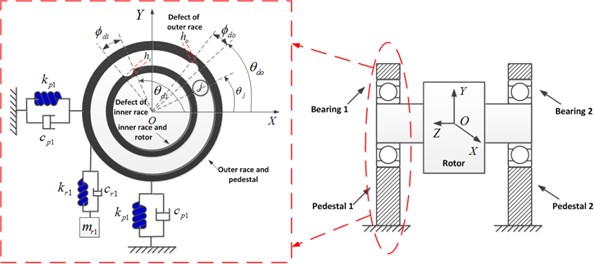
The nonlinear restoring forces of bearing, unbalanced force excitations and self-weight of the rotor are considered in the dynamic model. By applying the energy theorem and Lagrange equation, a series of two order differential equations describing rotor vibrations are derived as follows:
In which , represent the coefficients of unbalanced excitation and rotor’s self weight. For 0, 1, it means that the self-weight of the rotor is the dominant force (weight-dominant condition). When 1, 0, the unbalanced forces are dominant among the external excitations (unbalance-force-dominant condition). In the following, the nonlinear supporting forces of the rolling bearing with and without localized defects will be derived accordingly.
3. Nonlinear supporting forces of localized defective ball bearings
Here, the bearing 1 is taken as an example to show the derivation of bearing supporting forces utilizing the Hertz contact theory. The bearing has the number of balls, and the th ball’s location angle at time t could be expressed as follows:
In which the orbital speed of the ball. For the pure rolling state, the relation between the orbital speed and rotor speed could be given by:
where the ball diameter and the pitch diameter of the bearing.
From the dynamic model shown in Fig. 1, the relative vibrational displacements between the inner race and bearing pedestals along the two transversal directions are expressed by (-) and (-), respectively. Considering the radial clearance of the bearing, the contact deformation for the th ball at time is calculated by:
The localized defects appear in the bearing raceways, as shown in Fig. 1. Obviously, additional clearance would be induced by these localized defect. This means that the expression of contact deformation in Eq. (4) should be modified to consider the additional clearance when the rolling ball contacts with the defective raceways. The actual shape of the defect is very complex. Here, without loss of generality, the half sinusoidal function is utilized to simplify the defect shape. For the outer and inner race defects, we use the , and ho and , and to describe their locations, sizes and depths, respectively. Thus, as long as the ball is contacting with the outer race defect, the contact deformation should be modified as follows:
In this study, the outer race is fixed to the bearing pedestal, and thus the outer race defect has constant location angle . However, for the inner race defect, its location angle becomes time-variant because the inner race rotates with the rotor shaft. In this case, the location angle is expressed as , in which the initial angle with respect to the axis at time 0. Except for this, the modified contact deformation is similar with that of the outer race defect in Eq. (5) by substituting the , , to the , , .
After the contact deformation obtained, the contact force between the rolling ball and inner raceways is calculated based upon the classical Hertz contact theory:
where the judge factor of contact state. For 0, 1; otherwise, 0. The represents the Hertzian contact stiffness. According the results of Harris [17], the stiffness value could be gained after the comprehensive curvature radius, elastic modulus and Poisson’s ratio of the contact pairs determined. Considering the number of balls in contact, the supporting forces of the bearing 1 along the two transversal directions could be derived as follows:
The above derivation mainly aims to the bearing 1. Similarly, for bearing 2, one can also obtain its supporting forces as:
The determination of , , is similar with that of , , , as given in the above equations.
After considering the Hertz contact, bearing clearance and localized defects, the supporting forces induced by rolling bearings are nonlinear and time variable. Thus, the vibration model of rotor-bearing system (see Eq. (1)) should be solved using the numerical integration method, i.e. the Runge-Kutta method. The fault characteristics of the vibrational signal for the rotor-bearing system under various load conditions will be simulated in the following section. Both the weight-dominant and unbalance-force-dominant conditions will be considered in order for comparisons.
4. Dynamic tests
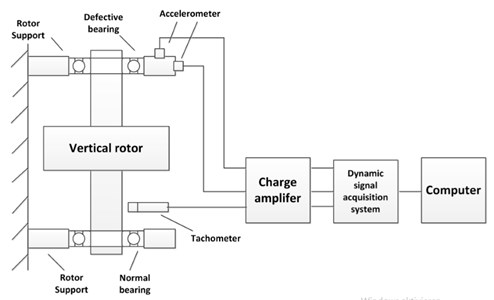
Most current studies focused on the fault diagnosis of defective rolling bearings under weight-dominant condition. The corresponding response signal and fault frequencies have been extensively analyzed and summarized. Thus, the dynamic tests will be carried out on the unbalance-force-dominant rotor-bearing system. For the vertical rotor, the self weight is along the axial direction and has no component in the two transversal directions. In this case, the unbalanced forces might be dominant. Thus, a vertical rotor system is chosen for dynamic tests and the schematic diagram is given in Fig. 2. The experimental system consists of a DC motor, a flexible shaft, a rotating disk and two deep groove rolling bearings (6208). In the test, the rotating disk is supported by the rolling bearing, and driven by a DC motor. The unbalanced force excitation is realized through mounting unbalanced mass on the disk. A tachometer is utilized to record the rotating speed. Two acceleration sensors are mounted on two transversal directions of the pedestal. Dynamic charge signals from the sensors are amplified and acquired by the dynamic signal acquisition system. For the sensors used in the test, the value of sensitivity parameter is about 100 g/mV. The actual acceleration signal (unit: g) could be gained by transferring the analog voltage signal to the acceleration signal through the sensitivity parameter. Sampling frequency is set to be 10 KHz. The physical picture of the test system is shown in Fig. 3.
Fig. 2Schematic diagram for the experimental system
The system parameters used in the dynamic simulation are listed in Table 1. From the values listed in the table, one can calculate the orbital frequency of the cage is 0.41 . Thus, the ball passing frequency of the outer race (BPFO) is 4.1 , and the ball passing frequency of inner race (BPFI) is expressed as 5.9 . In the following, one will see how the fault characteristic frequencies of bearing defects vary when the condition changes from the weight-dominant condition to the unbalance-force-dominant condition.
Fig. 3Physical picture of the experimental system

Table 1System parameters
Parameters | Values | Parameters | Values |
Rotor mass (Kg) | 3 | Number of balls | 10 |
Rotor damping (N/s) | 1200 | Radial clearance (m) | 1e-5 |
Rotor stiffness (N/m) | 1e6 | Pedestal mass (Kg) | 12.638 |
Unbalanced mass (Kg) | 0.01 | Pedestal stiffness (N/m) | 15e6 |
Mass eccentricity (m) | 5e-4 | Pedestal damping (N/s) | 2210 |
Bearing pitch diameter (m) | 0.06 | Springs mass (Kg) | 1 |
Ball diameter (m) | 0.0108 | Springs damping (N/s) | 9500 |
Contact stiffness (N/m3/2) | 8e9 | Springs stiffness (N/m) | 8e9 |
Axial stiffness (N/m) | 1e9 |
5. Discussions
5.1. Weight-dominant condition (Only rotor’s self-weight)
In this section, only rotor’s self-weight is considered and thus the weight dominant condition is in operation, i.e. 0, 1. The rolling bearing considered in this study is deep groove type, and its contact angle is zero. This means that the coupling between the transversal and axial vibrations is weak. Thus, in the following simulations, the transversal vibrations will be mainly considered.
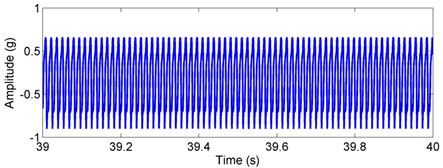
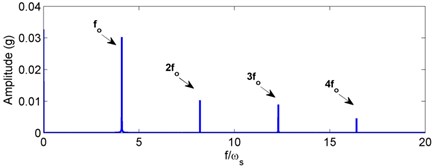
The values of defect parameters are given: 0.1 rad, 1e-3 rad, 1e-3 m for the outer race defect and 0.1 rad (initial angle with respect to the axis at time 0), 1e-3 rad, 1e-3 m for the inner race defect. As the acceleration sensor is used in the dynamic test, so the acceleration signal is gained in the test. In order for comparisons, the simulated signal should also be the acceleration signal. Using the numerical integration method, the vibration displacement and velocity are computed accordingly. By differencing the vibration velocity with time, the vibration acceleration is then obtained for comparison with the test results. The simulated acceleration signal and corresponding envelope spectra for the outer/inner race defects under weight-dominant condition are, respectively, given in Figs. 4 and 5. For the outer race defect, one can see from Fig. 4 that there is a series of impulse with equal amplitudes and intervals in the vibrational signal. The characteristic frequencies could be expressed by ( 1, 2, 3, ...), where is the BPFO. When the inner race has a localized defect, it is found from Fig. 5 that amplitude modulation appears in the vibrational signal, and side bands could be seen in the envelope spectra. The characteristic frequencies are the combinations of (BPFI) and rotating frequency , i.e. (, 0, 1, 2, ...). From Figs. 4 and 5, one can easily find these identified characteristic frequencies. Currently, most studies focused on the fault diagnosis of rolling bearings under weight-dominant condition [1-8]. The obtained fault characteristic frequencies are consistent with current results, indicating that the present dynamic model is reasonable.
Fig. 4Simulated acceleration response and envelop spectra for the outer race defect under weight dominant condition: a) time response, b) envelope spectra. (X-axis direction)
a)
b)
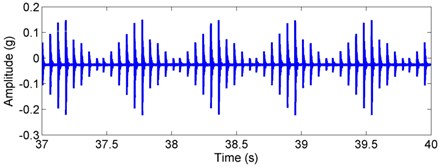
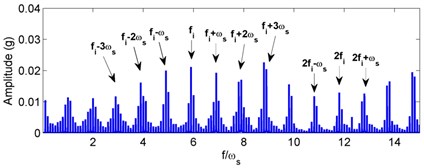
Fig. 5Simulated acceleration response and envelop spectra for the inner race defect under weight dominant condition: a) time response, b) envelope spectra. (X-axis direction)
a)
b)
5.2. Unbalance-force-dominant condition (Only unbalanced force excitation)
For the vertical rotating machinery, the self weight is along the axial direction and has no component in the two transversal directions. In the aero engine, the rotor’s gravity force is relatively smaller because of the widely used thin-walled rotating structures. In order to simulate the unbalance-force-dominant condition, only the unbalanced force is considered in this section, i.e. 1, 0. From Eq. (1), the self-weight force is along the axial direction ( axis). Due to the weak coupling between the transversal and axial vibrations, the transversal vibrations of the rotor are still the focus in the following simulation and experiment analysis.
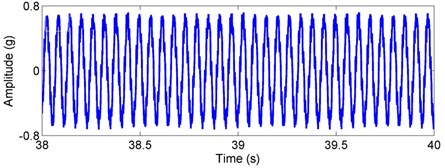
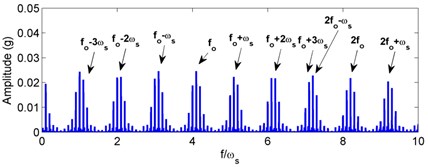
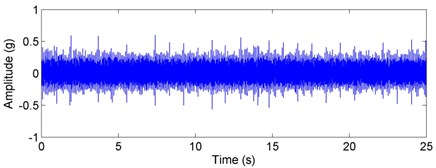
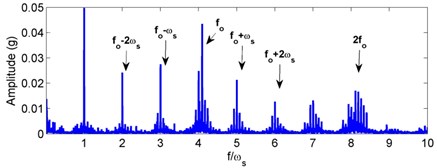
For the outer race defect, the simulated acceleration signal and corresponding envelope spectra are plotted in Fig. 6. Dynamic tests on a vertical rotor-bearing system are also conducted and the results are given in Fig. 7. Compared with the weight-dominant condition (see Fig. 4), one can find that the time signal and fault frequencies differ distinctly for the unbalance-force-dominant condition. It is shown from Fig. 6 that the signal mainly contains the unbalanced response and sidebands are found in the envelop spectra. Fault characteristic frequencies for the outer race defect under unbalance-force-dominant condition could be summarized as: (, 0, 1, 2, ...). In the tested spectra, one can also find these frequencies, as marked in Fig. 7. Thus, the simulation results are verified by the dynamic test.
Fig. 6Simulated acceleration signal and envelop spectra for the outer race defect under unbalance-force-dominant condition: a) time response, b) envelope spectra. (X-axis direction)
a)
b)
Fig. 7Experimental acceleration signal and envelop spectra for the outer race defect under unbalance-force-dominant condition: a) time response, b) envelope spectra. (X-axis direction)
a)
b)
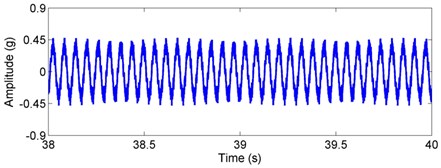
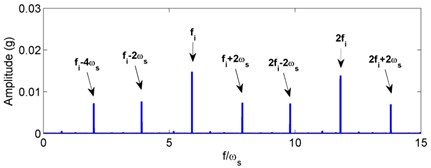
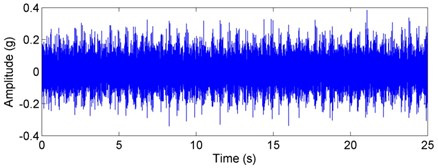
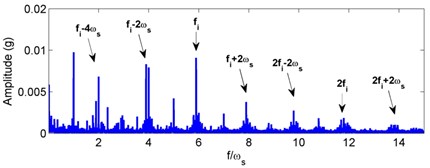
For the inner race defect, both the simulated and tested results are shown in Figs. 8 and 9, respectively. Compared with the weight-dominant condition (see Fig. 5), the time signal for the unbalance-force-dominant condition mainly contains the unbalanced response. Although the fault frequencies are still the combinations of BPFI and rotating frequency, the difference is that only the even times of rotating frequency are found in the sidebands. These frequencies are summarized as: (, 0, 1, 2, ...), and could also be found in the test results of Fig. 9. Thus, the simulation results are also verified by the dynamic test.
Fig. 8Simulated acceleration signal and envelop spectra for the inner race defect under unbalance-force-dominant condition: a) time response, b) envelope spectra. (X-axis direction)
a)
b)
Fig. 9Experimental acceleration signal and envelop spectra for the inner race defect under unbalance-force-dominant condition: a) time response, b) envelope spectra. (X-axis direction)
a)
b)
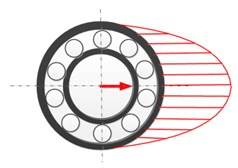
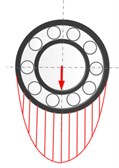
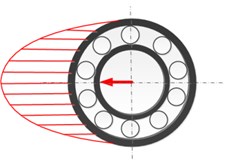
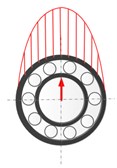
From the above numerical and experimental analysis, the fault characteristic frequencies for both the outer and inner race defects under unbalance-force-dominant condition could be summarized as: (, 0, 1, 2, ...) for the outer race defect and (, 0, 1, 2, ...) for the inner race defect. One can find that the fault characteristic frequencies are all modulated by the rotating frequency besides the BPFO and BPFI. This is mainly because that the load zone of the rolling bearing induced by the unbalance force varies with time. Fig. 10 shows the variation of bearing load zone with rotation. Even for the outer race defect, although the defect holds still, the load zone rotates with the inner shaft and the modulation occurs in the fault characteristics. For the inner race defect, both the load zone and defect are all rotating, which causes the characteristic frequencies more complicate and even times of rotating frequency found in the modulation. Therefore, one can find that the fault characteristics of localized defects indeed have distinct differences with that of the weight-dominant condition, in which the load zone maintains constant.
Fig. 10Schematic diagram for the variation of bearing load zone with rotation under unbalance-force-dominant condition: a) ωst= 0, b) ωst=π/2, c) ωst=π, d) ωst=3π/2
a)
b)
c)
d)
6. Conclusions
Vibration signal modeling of a localized defective rolling bearing under unbalanced force excitations is carried out and the fault characteristics are studied. Through envelope analysis, the fault characteristic frequencies of inner/outer raceway defects with and without unbalanced force excitations are presented. Detailed comparisons through dynamic simulations and tests show that the unbalanced force excitations have significant influence on the fault characteristic frequencies:
1) Fault characteristic frequencies for the outer race defect under non-weight dominant condition are expressed as (, 0, 1, 2, ...).
2) For the inner race defect, its fault frequencies are still the combinations of BPFI and rotating frequency, the difference is that only the even times of rotating frequency are found in the sidebands. These frequencies are summarized as: (, 0, 1, 2, ...).
References
-
Sopanen J., Mikkola A. Dynamic model of a deep-groove ball bearing including localized and distributed defects, Part 1: Theory. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, Vol. 217, Issue 3, 2003, p. 201-211.
-
Sopanen J., Mikkola A. Dynamic model of a deep-groove ball bearing including localized and distributed defects, Part 2: implementation and results. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, Vol. 217, Issue 3, 2003, p. 213-223.
-
Zeki K., Hira K. Simulation and analysis of vibration signals generated by rolling element bearing with defects. Tribology International, Vol. 36, 2003, p. 667-678.
-
Patel V. N., Tandon N., Pandey R. K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races. Journal of Tribology, Vol. 132, Issue 4, 2010, p. 41101.
-
Betea B., Dobra P., Trusca M. Simplified mathematical model of the bearings with defects. 16th International Conference on System Theory, Control and Computing, 2012.
-
Kankar P. K., Sharma S. C., Harsha S. P. Fault diagnosis of high speed rolling element bearings due to localized defects using response surface method. Journal of Dynamic Systems, Measurement, and Control, Vol. 133, Issue 3, 2011, p. 200-205.
-
Rafsanjania A., Abbasiona S., Farshidianfarb A. Nonlinear dynamic modeling of surface defects in rolling element bearing systems. Journal of Sound and Vibration, Vol. 319, 2009, p. 11501174.
-
Ashtekar A., Sadeghi F., Stacke L. E. Surface defects effects on bearing dynamics. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 224, 2010, p. 25-35.
-
Sawalhi N., Randall R. B. Simulating gear and bearing interactions in the presence of faults. Part I. The combined gear bearing dynamic model and the simulation of localized bearing faults. Mechanical Systems and Signal Processing, Vol. 22, 2008, p. 19241951.
-
Sawalhi N., Randall R. B. Simulating gear and bearing interactions in the presence of faults: Part II: Simulation of the vibrations produced by extended bearing faults. Mechanical Systems and Signal Processing, Vol. 22, Issue 8, 2008, p. 1952-1966.
-
Immovilli F., Bianchini C., Cocconcelli M. Bearing fault model for induction motor with externally induced vibration. IEEE Transactions on Industrial Electronics, Vol. 60, Issue 8, 2013, p. 3408-3418.
-
Niu L., Cao H., He Z. Dynamic modeling and vibration response simulation for high speed rolling ball bearings with localized surface defects in raceways. Journal of Manufacturing Science and Engineering, Vol. 136, Issue 4, 2014, p. 41015.
-
Singh S., Kpke Howard U. G. C. Q., et al. Analyses of contact forces and vibration response for a defective rolling element bearing using an explicit dynamics finite element model. Journal of Sound and Vibration, Vol. 333, Issue 21, 2014, p. 5356-5377.
-
Zhao S. F., Liang L., Xu G. H. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method. Mechanical Systems and Signal Processing, Vol. 40, Issue 1, 2013, p. 154-177.
-
Borghesani P., Ricci R., Chatterton S. A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions. Mechanical Systems and Signal Processing, Vol. 38, Issue 1, 2013, p. 23-35.
-
Muruganatham B., Sanjith M. A., Krishnakumar B. Roller element bearing fault diagnosis using singular spectrum analysis. Mechanical Systems and Signal Processing, Vol. 35, Issue 1, 2013, p. 150-166.
-
Harris T. A., Kotzalas M. N. Rolling Bearing Analysis Taylor and Francis, Boca Raton, 2007.
About this article
The research work described in this paper was supported by Natural Science Foundation of China under Grant No. 11472147.
