Abstract
An important problem in the design of printing equipment is measurement of vibrations of rollers and also of their segments in the designed folding machines. Such measurements were carried out in the process of this investigation. Laser displacement head “Microtrack LTC 200-100” was applied during the process of performed measurements. Results from the experiment were obtained and analyzed at the pre-selected positions of the investigated rollers and also of their segments. Vibrational displacements were determined (they have the form of beatings) of the investigated rollers and also of their segments, which originate during the process of rotation. They influence the quality of resulting printing products. Plane stress problem by taking into account orthotropic properties of material is analyzed. Supplementary stiffness, which takes place because of the static loading as a result of action of centrifugal forces, is used in the analyzed model. Eigenmodes are calculated and analyzed.
1. Introduction
An important problem in the design of printing equipment is measurement of vibrations of rollers and also of their segments in the folding machines. Such measurements were carried out in the process of this investigation. Laser displacement head “Microtrack LTC 200-100” was applied during the process of performed measurements. Results from the experiment were obtained and analyzed at the pre-selected positions of the investigated rollers and also of their segments. Vibrational displacements were determined (they have the form of beatings) of the investigated rollers and also of their segments, which originate during the process of rotation. They influence the quality of resulting printing products.
Plane stress problem by taking into account orthotropic properties of material is analyzed. Supplementary stiffness, which takes place because of the static loading as a result of action of centrifugal forces, is used in the analyzed model. Eigenmodes are calculated and analyzed.
This paper presents a continuation of the previous analysis performed by the authors. Basic results from earlier investigations have been presented in [1-3]. Experimental setup was designed and developed and the performed experimental procedure was implemented on the basis of the material, which is presented in [4-7]. The performed numerical analysis is based on the procedure described in the earlier papers of the authors as well as on the material presented in [8-11]. Related engineering problems are described and investigated in other papers of various authors [12-22].
Thus, the aim of the authors of this paper is to determine the level of wear of rollers located in the folding machine by performing measurements of the displacements of surfaces of the investigated rollers.
2. Numerical procedure for the analysis of plane vibrations of a rotating orthotropic element of the investigated structure
Further in this paper and denote the axes of the orthogonal system of coordinates. Firstly, the plane stress problem is solved. The stiffness matrix of this problem has the usual form:
where is used to denote the thickness of the analyzed structure and also:
where , ,…, are used to denote the conventional shape functions of the applied finite element (two dimensional Lagrange element with quadratic approximation is used). The transformation matrix for the investigated problem has the conventional form:
where the assumed directions of orthotropic qualities of the investigated material for this problem are coinciding with the radial direction and with the angular direction of the circular element of the folding machine. On the basis of the described assumptions it is considered that the following equalities hold:
The matrix of physical parameters describing the elastic properties of the analyzed material having orthotropic qualities is assumed to have the form:
where , are modulus of elasticity in the directions of the axes of orthotrophy and , are Poisson’s ratios of the orthotropic material. Also, as usual for orthotropic materials it is assumed that the following relationship is true:
The loading vector for the static problem which is caused by the centrifugal forces that take place for the angular velocity equal to one, that is 1 rad/sec is of the form presented further:
where is used to denote the density of the material of the analyzed element of the folding device and the matrix of the previously described shape functions has the conventional form, that is:
By performing the solution of the system of linear algebraic equations the static displacements for the loading force which was previously described in detail and is caused by the centrifugal forces the vector of nodal displacements of the elastic structure is obtained.
Then it is necessary to calculate the supplementary stiffness matrix which is caused by the previously described centrifugal loading. This matrix has the conventional form presented further:
where it is denoted that:
And also, it is assumed that:
This expression involves the stresses, which are to be calculated on the basis of the relationship presented further:
The full stiffness matrix is to be determined finally. This matrix is obtained for rotation by the angular velocity It is of the form presented further:
Finally, the mass matrix is required. For the analyzed problem, it is of the conventional form presented further:
3. Eigenmodes of plane vibrations of the rotating orthotropic element of the investigated element of the folding machine
The analyzed element of the folding machine has the shape of a circle with the internal radius having the value of 0.02 m and the external radius having the value of 0.04 m. In the present investigation, it is considered that the thickness of the investigated element of the folding machine has the value 0.0001 m. The following boundary conditions are assumed: all displacements of the nodes are considered to be equal to zero (that is the structure is fastened) on the internal radius of the analyzed element of the folding machine. It is considered that the physical parameters of the investigated element of the folding machine have the following values: elastic modulus 0.34·109 Pa, the two Poisson’s ratios 0.4 and also 0.14, density of the investigated material of the analyzed element of the folding machine 785 kg/m3.
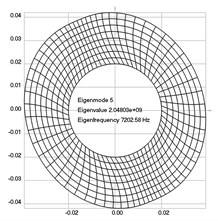
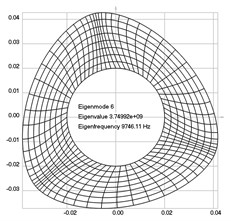
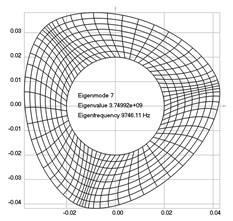
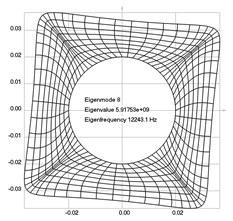
The first eigenmodes were calculated and for the value of 0 rad/sec are represented in Fig. 1.
Fig. 1Eigenpairs when the analyzed element of the folding machine does not experience rotation: a) the first, b) the second, …, i) the ninth eigenpairs
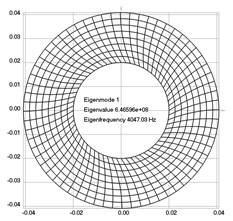
a)
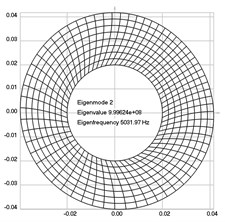
b)
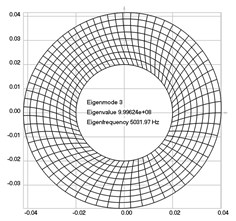
c)
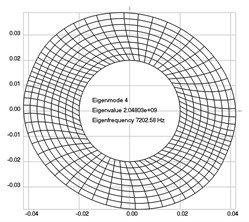
d)
e)
f)
g)
h)
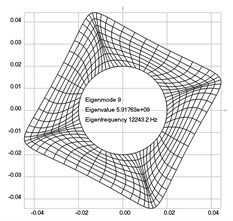
i)
The first eigenmodes were calculated and for the value of rad/sec are represented in Fig. 2.
Fig. 2Eigenpairs when the analyzed element of the folding machine does experience rotation: a) the first, b) the second, …, i) the ninth eigenpairs
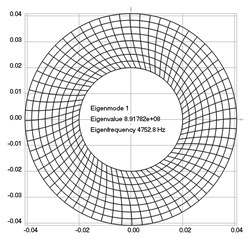
a)
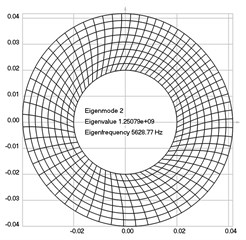
b)
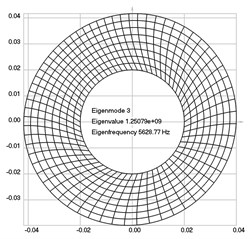
c)
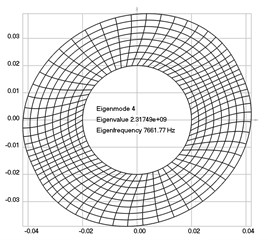
d)
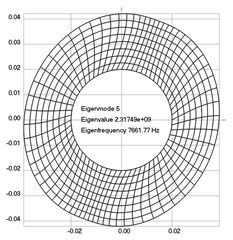
e)
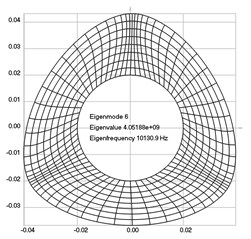
f)
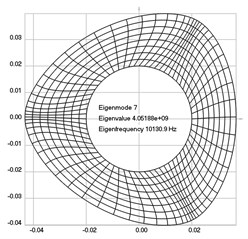
g)
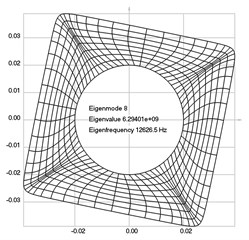
h)
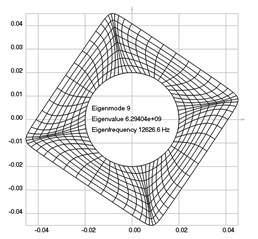
i)
The element of the folding machine with interchanged qualities of the orthotropic material was also analyzed. The following parameters of the element of the folding machine were taken into account: elastic modulus Pa, the two Poisson’s ratios 0.14 and also 0.4.
The first eigenmodes were calculated and for the value of 0 rad/sec are represented in Fig. 3.
The first eigenmodes were calculated and for the value of rad/sec are represented in Fig. 4.
From the obtained numerical results of performed analysis it is determined that the change of the physical parameters of the investigated element of the folding machine does have a substantial and evident effect to the shapes of the higher eigenmodes of the investigated element of the folding machine.
Fig. 3Eigenpairs when the analyzed element of the folding machine does not experience rotation: a) the first, b) the second, …, i) the ninth eigenpairs
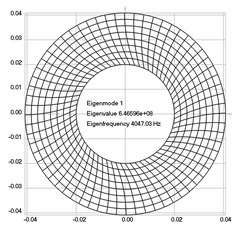
a)
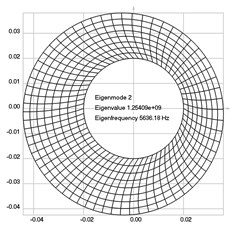
b)
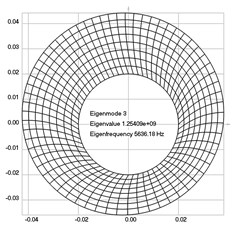
c)
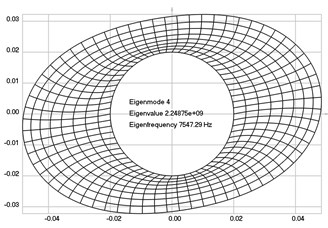
d)
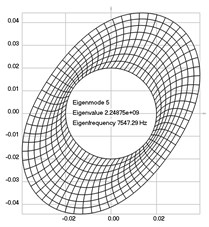
e)
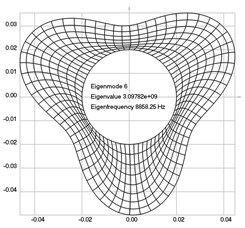
f)
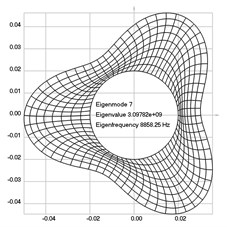
g)
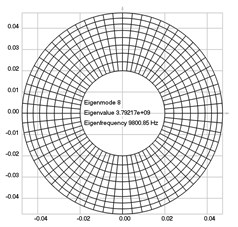
h)
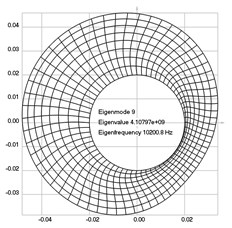
i)
4. Results of experimental investigations of vibrations of the rollers of the element of the folding machine
In the described experimental investigation measurements of vibrations of the elements of the analyzed folding machine, that is of rollers and also of their segments, were performed by using the proposed and developed experimental setup. This setup involves the laser head for performing the measurement of the required displacements of the type “Microtrack LTC 200-100”. Various methods of supplying of rotational motion to the rollers can be considered. In the presented and performed analysis the rollers were supplied by rotational motion manually. Results of performed measurements were transferred to and registered by a personal computer. Measurements of displacements of the analyzed rollers of the folding machine were performed at various pre-selected points, some of the typical points are indicated in Fig. 5. Results of performed measurements after this were processed by applying a special filter for low frequencies. Thus, it was possible to separate low frequency vibrations, which show the displacements of the investigated roller of the folding machine and of its segments in the process of performed measurements. Detailed description of the developed devices used in the experimental setup, as well as of the proposed experimental procedure, also the choice of the points in which analysis and measurements are performed, the use of the special digital filtering procedure and the choice of the type and special parameters of the applied digital filter are presented in the previous investigations as well as papers of the authors.
Fig. 4Eigenpairs when the analyzed element of the folding machine does experience rotation: a) the first, b) the second, …, i) the ninth eigenpairs
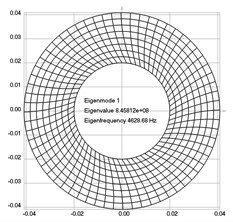
a)
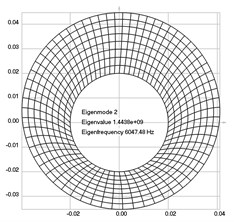
b)
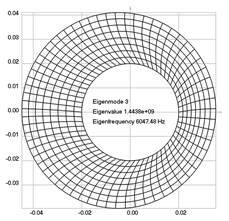
c)
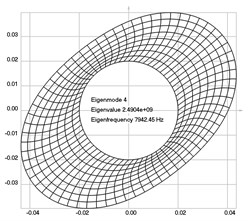
d)
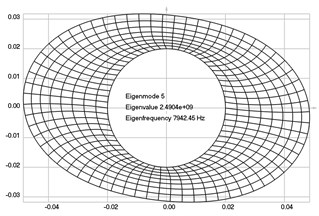
e)
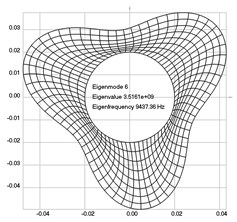
f)
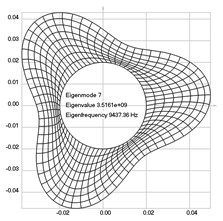
g)
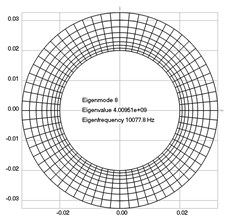
h)
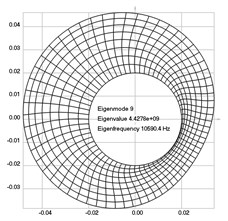
i)
Fig. 5General view of 8 pockets of the analyzed folding device and locations of pre-selected points at which measurements were performed (1-4)

Further some of the obtained typical results of analysis when the rollers of the investigated folding machine are rotated manually are shown. In Fig. 6 the results obtained when performing the procedure of measurements of the investigated displacements at some of the typical pre-selected points of measurement of the rollers of the investigated folding machine are presented.
The obtained results of performed analysis and measurements were investigated in detail. It is evident that vibrational motions and processes of various types take place and can be seen in the analyzed element of the folding machine. But after successful processing of results and application of the proposed low pass digital filter and after the process of choosing of suitable parameters of this digital filter it is possible to obtain low frequency vibrations. They satisfactorily correspond with the natural vibrations obtained previously and represented by the eigenpairs.
Fig. 6Typical results of obtained measurements of the analyzed displacements of rollers of the folding machine at pre-selected points of analysis
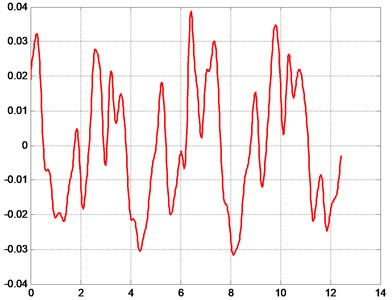
a) Measurement performed at position number 1, resulting displacement (mm) is a function of time (sec)
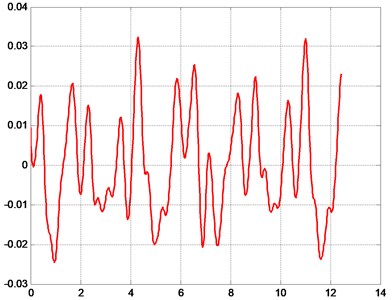
b) Measurement performed at position number 2, resulting displacement (mm) is a function of time (sec)
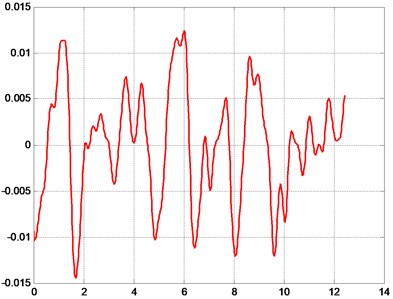
c) Measurement performed at position number 3, resulting displacement (mm) is a function of time (sec)
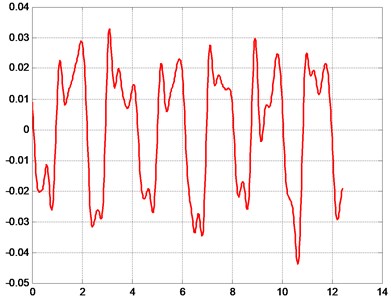
d) Measurement performed at position number 4, resulting displacement (mm) is a function of time (sec)
5. Conclusions
Measurements of vibrations of the rollers of the folding machine and also of their segments were carried out in the process of this investigation. Laser displacement head “Microtrack LTC 200-100” was applied during the process of performed measurements. In the presented procedure of investigations, the rollers of the folding machine were rotated manually. Results of the performed measurements were transferred to and then registered by using a personal computer. Results from the experiment were obtained and analyzed at the pre-selected positions of the investigated rollers and also of their segments. Results of those measurements were processed by applying a low frequency filter of special type, thus separating vibrations of low frequency, which reflect the displacements of the analyzed roller of the folding machine and of its segments in the process of performed measurements.
Plane stress problem by taking into account orthotropic properties of material is analyzed. Supplementary stiffness, which takes place because of the static loading as a result of action of centrifugal forces, is used in the analyzed model. Eigenmodes are calculated and analyzed.
Two problems with different values of physical parameters were analyzed in this paper. From the obtained and presented results it is seen that the change of the physical parameters does have a substantial effect to the higher eigenmodes of the element of the folding machine.
The obtained results of performed analysis and measurements were investigated in detail. It is evident that vibrational motions and processes of various types take place and can be seen in the analyzed element of the folding machine. But after successful processing of results and application of the proposed low pass digital filter and after the process of choosing of suitable parameters of this digital filter it is possible to obtain low frequency vibrations. They satisfactorily correspond with the natural vibrations obtained previously and represented by the eigenpairs.
The obtained results of analysis are used in the process of design of rollers of the folding machines and of their elements. Also, these results which were obtained during the performed investigations allow to predict and determine the time when it is already necessary to carry out the process of renewal of obsolete rollers of the folding machine in order to ensure that the folding of printing products would be performed qualitatively.
References
-
Kibirkštis E., Miliūnas V., Havenko S., Ragulskis K., Ragulskis L. Measurement of longitudinal vibrations of the rollers in a folding machine. Journal of Measurements in Engineering, Vol. 5, Issue 1, 2017, p. 40-48.
-
Ragulskis K., Ragulskis L., Kibirkštis E., Augutis S. V., Vainilavičius D., Miliūnas V., Pauliukaitis D. Measurement of vibrations of rotating elements in a folding machine. Journal of Measurements in Engineering, Vol. 3, Issue 1, 2015, p. 9-16.
-
Kibirkštis E., Augutis S. V., Vainilavičius D., Miliūnas V., Pauliukaitis D., Ragulskis L. Effect of dynamic regime of rollers of pocket folding machine to quality of printing products. Journal of Vibroengineering, Vol. 17, Issue 6, 2015, p. 2869-2881.
-
Peiponen K. E., Myllyla R., Priezzhev A. V. Optical Measurement Techniques – Innovations for Industry and the Life Sciences. Springer, 2009, p. 155.
-
Jayakumar T., Thavasimuthu M. Practical Non-Destructive Testing. Cambridge: Woodhead, 2002, p. 184.
-
Rastogi P. K. Optical Measurement Techniques and Applications. Artech House Incorporated, 1997, p. 433.
-
Technical Characteristics of Laser Displacement Measurement Head “Microtrack LTC 200-100”. http://mtiinstruments.com/pdf/products/microtrak2sal.pdf.
-
Bathe K. J. Finite Element Procedures in Engineering Analysis. Prentice-Hall, New Jersey, 1982.
-
Zienkiewicz O. C. The Finite Element Method in Engineering Science. Mir, Moscow, 1975, (in Russian).
-
Castro J., Ostoja-Starzewski M. Elasto – plasticity of paper. International Journal of Plasticity, Vol. 19, 2003, p. 2083-2098.
-
Levy S., Wilkinson J. P. D. The Component Element Method in Dynamics with Application to Earthquake and Vehicle Engineering. McGraw-Hill, New York, 1976.
-
Huang H., Hagman A., Nygards M. Quasi static analysis of creasing and folding for three paperboards. Mechanics of Materials, Vol. 69, Issue 1, 2014, p. 11-34.
-
Barbier C., Larsson P. L., Östlund S. Numerical investigations of folding of coated papers. Composite Structures, Vol. 67, Issue 4, 2005, p. 383-394.
-
Barbier C., Larsson P. L., Östlund S. On dynamic effects at folding of coated papers. Composite Structures, Vol. 67, Issue 4, 2005, p. 395-402.
-
Barbier C., Larsson P. L., Östlund S. Experimental investigation of damage at folding of coated papers. Nordic Pulp and Paper Research Journal, Vol. 17, Issue 1, 2002, p. 34-38.
-
Sim K., Youn H. J., Oh K. D., Lee H. L., et al. Fold cracking of coated paper: the effect of pulp fiber composition and beating. Nordic Pulp and Paper Research Journal, Vol. 27, Issue 2, 2012, p. 445-450.
-
Dai J. S., Medland A. J., Mullineux G. Carton erection using reconfigurable folder mechanism. Packaging Technology and Science, Vol. 22, Issue 7, 2009, p. 385-395.
-
Yao W., Cannella F., Dai J. S. Automatic folding of cartons using a reconfigurable robotic system. Robotics and Computer – Integrated Manufacturing, Vol. 27, Issue 3, 2011, p. 604-613.
-
Mullineux G., Feldman J., Matthews J. Using constraints at the conceptual stage of the design of carton erection. Mechanism and Machine Theory, Vol. 45, Issue 12, 2010, p. 1897-1908.
-
Sirkett D. M., Hicks B. J., Berry C., Mullineux G., Medland A. J. Simulating the behavior of folded cartons during complex packing operations. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 220, Issue 12, 2010, p. 1797-1811.
-
Liu H., Dai J. An approach to carton – folding trajectory planning using dual robotic fingers. Robotics and Autonomous Systems, Vol. 42, Issue 1, 2003, p. 47-63.
-
Gidlöf V. In press conditions and their effect on runnability and convertability in digital package printing. Packaging Technology and Science, Vol. 18, Issue 4, 2005, p. 189-197.
About this article
All authors declare that all of them have made contributions to the paper. So, contributions of all coauthors are acknowledged. The authors thank the reviewers for their valuable comments. They enabled to improve the paper. The work was carried out on the basis of the Contract No. F5-90-1389.
