Abstract
Acoustic emission (AE) technique has been widely used for the classification of rub-impact in rotating machinery due to its high sensitivity, wide frequency response range and dynamic detection property. However, it is still unsatisfied to effectively classify the rub-impact in rotating machinery under complicated environment using traditional classification method tailored to a single AE sensor. Recently, motivated by the theory of compressed sensing, a sparse representation based classification (SRC) method has been successfully used in many classification applications. Moreover, when dealing with multiple measurements the joint sparse representation based classification (JSRC) method could improve the classification accuracy with the aid of employing structural complementary information from each measurement. This paper investigates the use of multiple AE sensors for the classification of rub-impact in rotating machinery based on the JSRC method. First, the cepstral coefficients of each AE sensor are extracted as the features for the rub-impact classification. Then, the extracted cepstral features of all AE sensors are concatenated as the input matrix for the JSRC based classifier. Last, the backtracking simultaneous orthogonal matching pursuit (BSOMP) algorithm is proposed to solve the JSRC problem aiming to get the rub-impact classification results. The BSOMP has the advantages of not requiring the sparsity to be known as well as deleting unreliable atoms. Experiments are carried out on real-world data sets collected from in our laboratory. The results indicate that the JSRC method with multiple AE sensors has higher rub-impact classification accuracies when compared to the SRC method with a single AE sensor and the proposed BSOMP algorithm is more flexible and it performs better than the traditional SOMP algorithm for solving the JSRC method.
1. Introduction
Rub-impact classification is one of the most important issues in the research filed of large rotating machinery. Traditional rub-impact classification techniques use vibration signals, which have some technical defects especially in the early rubbing stage [1]. Acoustic emission (AE) technique provides a new approach for the rub-impact classification because of its unique advantages, such as high sensitivity, wide frequency response range and dynamic detection property [2]. During the past few years, plenty of methods have been proposed in order to extract robust features of the AE signal employed in the rub-impact classification in rotating machinery. Modal acoustic emission (MAE) derived from the traditional propagation theory is an effective way to express the AE signal [3]. Following the MAE theory, an analytic expression of the AE signal was given and then used as feature representation for the rub-impact classification [4]. A rub-impact classification method based on Gaussian mixture model (GMM) [5] was proposed in [6] using the cepstral coefficients of the AE signal as the input features. In [7], a new fractal dimension of the AE signal was used as the feature for the rub-impact classification, and simulation results demonstrated the effectiveness of the proposed wavelength based fractal dimension. However, it is still unsatisfied to effectively classify the rub-impact in rotating machinery under complicated environment using traditional classification method tailored to a single AE sensor.
Recently, a sophisticated classification approach based on the theory of sparse representation has been proposed in the fields of compressed sensing [8]. This sparse representation based classification (SRC) scheme represents the test sample as a linear sparse combination of the training samples and then classifies the test sample to the class which yields the minimum representative error [8]. The SRC method has been successfully used in many applications, such as face recognition [8], power system transient recognition [9] and hyperspectral image classification [10]. As an extension of the SRC method, the joint sparse representation based classification (JSRC) method has been proposed for the multiple measurements classification which uses not only the sparse property of each measurement but also the structural sparse information across the multiple measurements [11]. The JSRC method has demonstrated advantageous over the SRC method in the classification problems of multiple measurements [11], multimodality [12] and multiple features [13].
Inspired by the amazing performance of the JSCR method for the multiple measurements classification problem, in this paper we investigate the use of multiple AE sensors for the classification of rub-impact in rotating machinery with the aid of the JSRC method. We build a rub-impact test bed with multiple AE sensors in our laboratory. As far as we known, this is the first attempt to use the JSCR method for the classification of rub-impact in rotating machinery. Previous works rely on simultaneous orthogonal matching pursuit (SOMP) [14-16] for solving the JSRC method. However, the SOMP algorithm should have the knowledge of the sparsity in advance which makes the algorithm less flexible. Moreover, once an atom has been wrongly selected, it will not have the chance to be deleted. Accordingly, in this paper we propose a novel algorithm called backtracking SOMP (BSOMP), by employing the backtracking strategy [17] to compensate for these shortcomings.
The rest of this paper is organized as follows. Section 2 introduces cepstral coefficients which are extracted as features of the AE signal for the rub-impact classification, and then in Section 3 we give a brief review of the SRC method. In Section 4 we first present the JSRC method for the rub-impact classification in rotating machinery with multiple AE sensors and then propose a BSOMP algorithm for solving it. Experiments on real-world data sets collected from our laboratory are carried out in Section 5, and final conclusions are given in Section 6.
2. Feature extraction
Feature extraction plays an important role for rub-impact faults classification in rotating machinery. Previous works have demonstrated the effectiveness of using the cepstral coefficients of the AE signal as the features for the rub-impact classification [6]. So, in this paper, we use the cepstral coefficients of each AE measurement to be the features for the rub-impact classification. And in this section, we will describe the method for extracting the cepstral coefficients in details.
The analytic expression of the AE signal based on the modal acoustic emission (MAE) theory was derived in [4]. However, some AE mode waves would be separated or even disappeared in time domain due to different propagation speeds and different distances from source to sensors. So, it is reasonable to classify the rub-impact in rotating machinery using the frequency domain information with the filter banks. The frequency spectrum of the AE signals mainly concentrated form 100 kHz to 300 kHz, and different frequency bins provide different contributions for the rub-impact classification. This assumption is same as the speech recognition problem, so in this paper we employ the cepstral coefficients of the AE signal as the features for the rub-impact classification which have been proven to be effective as the frequency domain features for speech recognition. The procedure for extracting the cepstral coefficients is shown in Fig. 1 and explained in steps as the following [4]:
Step 1: Transform the input AE signal from the time domain to the frequency domain using the short-time Fourier transform (STFT):
where is the window function. In this paper, we use the Hanning window.
Fig. 1The procedure for extracting the cepstral coefficients
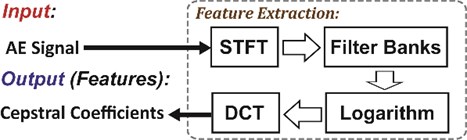
Step 2: Pass through the triangular filter banks and then calculate the output spectrum energy of each sub filter:
where is the number of the sub filters, is the frequency response of the th sub filter, and are the low frequency limit and the high frequency limit of the th sub filter respectively, is the energy normalization factor defined as:
The center frequencies of all the sub filters are equal distributed at the logarithm scale, meanwhile the low frequency limit and the high frequency limit of the th sub filter equal to the center frequency and of its two adjacent sub filters at the logarithm scale, respectively. Accounting for higher attenuation of the AE signal happening in the lower frequency band, the center frequency of th sub filter, the low frequency limit and the high frequency limit of the triangular filter banks should satisfy:
For AE signals we set 100 kHz and 300 kHz. From Eq. (4) we can get all the design parameters of the triangular filter banks.
Step 3: Following the logarithm operation and the discrete cosine transform (DCT), we can finally get the cepstral coefficients of the AE signal:
where is the desired order of the cepstral coefficients which usually ranges from 12 to 16. In this paper, we set 12 as suggested in [4].
3. The sparse representation based classification (SRC) method
Recently the sparse representation based classification (SRC) method motivated by the theory of compressed sensing [14-15] has been successfully used in many classification applications, such as face recognition [8], power system transient recognition [9] and hyperspectral image classification [10]. The basic idea of the SRC method is to correctly determine which class the test sample belongs to using the training samples collected from different classes with the sparse representation method [20]. This SRC scheme first constructs the dictionary using training samples, and then represents the test sample as a linear sparse combination of the dictionary atoms and finally classifies the test sample to the class which yields the minimum representative error [21]. The SRC approach is employed as a benchmark for the classification of rub-impact in rotating machinery with a single AE sensor in this paper.
In the SRC approach, all the training samples from the th class are arranged as the columns of a sub-dictionary matrix . We can define a dictionary which includes the entire set of the training samples from all the classes given as follows:
where is the total number of the training samples from all the classes, is the dimensionality of the cepstral coefficients extracted from its corresponding AE measurement.
The basic assumption of the SRC method is that the test sample lies in the linear span of the training samples from the same class. Suppose the test sample belongs to the th class linearly represented by all the atoms of the dictionary:
where is the representation vector, in which is the sub-representation vector associated with the sub-dictionary . In ideal situation when belongs to the th class , so can represent as , i.e., directly classified to the th class. However, in general case most of the representation coefficients are quite small while only the coefficients of the sub-representation vector have large values. This means that the test sample can be accurately classified to the th class by forcing the representation vector to be sparse, which leads to the l0-norm minimization problem:
For practical classification of the rub-impact in rotating machinery, we should account for the noises and rewrite the l0-norm minimization problem Eq. (8) as follows [22]:
However, the l0-norm minimization problem Eq. (9) is NP-hard which is hard to solve. In practice, problem Eq. (9) can be solved using the greedy algorithm [23-26] or relaxing to its convex l1-norm minimization form [27, 28]:
In this paper, we use the orthogonal matching pursuit (OMP) algorithm to solve the l0-norm problem Eq. (9), the general procedure of the OMP algorithm is described in Algorithm 1 [23]:
Algorithm 1 OMP.
Input: dictionary , test sample , maximum number of iteration , error threshold .
Initialization: the residual , the index set , the iteration counter 1.
whileand
1. Find the index
2. Set
3. Solve the least squares problem
4. Renew the residual
5.
end while
Output: the sparse representation vector equals to with the index in and 0 otherwise.
Having obtained the sparse representation vector , we can identify the test sample to the class with the minimum representative error. The procedure of the SRC method for the classification of rub-impact in rotating machinery with a single AE sensor is described as follows:
1) Use the feature extraction method described in Section 2 to get the training samples of all the classes to form dictionary and then normalize the columns of .
2) Use the feature extraction method described in Section 2 to get the test sample .
3) Solve the problem Eq. (9) using the OMP algorithm and get the sparse representation vector .
4) Calculate the representation error of each class:
5) The class associated with the smallest representation error is classified to be the right one:
4. The joint sparse representation based classification (JSRC) method
From the classification results of previous works [4, 6, 7], we can see that it is still unsatisfied to effectively classify the rub-impact in rotating machinery under complicated environment using traditional classification method tailored to a single AE sensor. Making a classification with multiple measurements using the joint sparse representation based classification (JSRC) method has shown its advantages to improve the classification accuracy in transient acoustic signal classification [11], so in this paper we investigate using the JSRC method for the classification of rub-impact in rotating machinery with multiple AE sensors.
In this section, we first present the JSRC problem formulation for the classification of rub-impact with multiple AE sensors and introduce the SOMP algorithm [15, 16] which is used in the previous work [14] to solve the JSRC problem. Then we propose an algorithm called BSOMP by employing the backtracking strategy [17] and provide the procedure of the JSRC method for rub-impact classification.
4.1. Problem formulation
As an extension of the SRC method, the general idea of the JSRC method is the same with the SRC method with the exception that not only using the sparse property of each measurement but also the joint sparse information across the multiple measurements [11]. Suppose the number of AE sensors is , then for each training sample there are measurements. So, in the JSRC method, the dictionary including the entire set of the training samples from all the classes can be defined as:
where is the number of the training samples of all the classes for each measurement, each sub-dictionary contains all training samples of all the classes from the th measurement.
In the JSRC method, the test sample is represented by a matrix which could be linearly represented by the dictionary:
where is the representation coefficient matrix.
There are two assumptions for the JSRC method [14]:
First the th measurement of the test sample should lie in the span of the training samples corresponding to the th measurement, i.e. the representation coefficient matrix should have a block-diagonal structure with the columns have the following structure:
where denotes a zero vector in , each subvector , lies in and denotes the number of the training samples for the th class.
Second the coefficients of the representation coefficient matrix corresponding to the measurements from the same training sample should be activated simultaneously to jointly and sparsely represent the test sample. For this assumption, we should transform the matrix to the sparse representation matrix by removing the zero coefficients of :
where denotes the matrix Hadamard product, the matrix and are defined as:
where is the vector of all ones and is the -dimensional identity matrix.
For the JSRC method, the matrix defined in Eq. (16) is constraint to be row wise sparse. Taking into the practical noises into consideration, this problem can be formulated as [14]:
where the l0\l2 norm is equals to the number of nonzero rows in the matrix.
However, the l0\l2 norm minimization problem Eq. (18) is also NP-hard. In practice, it can be solved using the greedy algorithm [16] or relaxing to the l1\l2 norm minimization problem [29, 30]:
4.2. SOMP algorithm
Previous work [14] uses the simultaneous orthogonal matching pursuit (SOMP) algorithm [15, 16] to solve the l0\l2 norm problem Eq. (18), and the general procedure of the SOMP algorithm is described in Algorithm 2.
Algorithm 2 SOMP.
Input: dictionary , test sample , maximum number of iteration , error threshold.
Initialization: the residual , the index set , the iteration counter 1.
whileand
1. Find the index
2. Set
3. Compute the orthogonal projector for 1,…,
4. Renew the residual
5.
end while
Output: the nonzero rows of the sparse representation matrix indexed by equal to .
4.3. BSOMP algorithm
The main drawback of the SOMP is that the sparsity should be known in advance. So cross-validation should be used in order to obtain a better classification result which makes the algorithm less flexible. Additionally, once the atom has been selected, it will not have the chance to be deleted even if it is a wrong one. In [17] backtracking strategy is employed to improve the OMP algorithm by detecting the previous chosen atoms’ reliability and then deleting the unreliable atoms. With the aid of backtracking strategy, no prior knowledge of the sparsity is needed, so in this paper we propose a BSOMP algorithm by incorporating the backtracking strategy with SOMP. The general procedure of the BSOMP algorithm is described in Algorithm 3.
Algorithm 3 BSOMP.
Input: dictionary , test sample , atom-adding threshold , atom-deleting threshold , error threshold .
Initialization: the residual , the index set , the iteration counter 1.
while
1. Find the candidate set by choosing all the indexes of atoms that satisfying
2. Compute the orthogonal projector for 1,…,
3. Find the candidate deleting set D by choosing all the indexed of atoms that satisfying
4. Set
5. Compute the orthogonal projector for 1,…,
6. Renew the residual
7.
end while
Output: the nonzero rows of the sparse representation matrix indexed by equal to .
4.4. The procedure of JSRC
The procedure of the JSRC method for the classification of rub-impact in rotating machinery with multiple AE sensors is described as follows:
1. Use the feature extraction method described in Section 2 to get the training samples of all the classes from measurements to construct dictionary and then normalize the columns of .
2. Use the feature extraction method described in Section 2 to get the test sample .
3. Solve the problem Eq. (18) using the SOMP/BSOMP algorithm and get the sparse representation matrix .
4. Calculate the representation error of each class:
5. The class associated with the smallest representation error is classified to be the right one:
5. Experiment
All the data for the experiment are collected in our laboratory. Data obtained from a rub-impact test bed for fault diagnosis of rotor are used in the paper as shown in Fig. 2(a). The test rig containing three bearings and two rubbing components can simulate two rub-impact faults at the same time through the steel arch case and the rub-impact screws in Fig. 2(a). The case is tightly fixed on the base support of the test rig by four fixed screws and drilled two rub-impact holes on the one side according to the size of the rub-impact screws. Also, the fault degree generated by rub-impact can be adjusted by screws. AE sensors with an operating range of 20 kHz to 1 MHz are marked as A, B, C and D form the left to the right respectively as shown in Fig. 2(b). The output signals from AE sensors are amplified to 40 dB. The AE signals are then passed through a band-pass filter 1 kHz-200 kHz to record AE signature rising from run-impact faults. The sampling rate for acquisition of AE signal waveforms is 2MSPS.
Fig. 2The data collection system

a) 3-bearing 2-span rotor system

b) AE signal collection system with 4 sensors
Three classes rub-impact events are simulated in the experiments: the non-rub-impact event sampled at common condition, the medium rub-impact event and the heavy rub-impact event. The number of the AE signals collected for each is 300, the maximum number of iteration and are all set to 15 and the error threshold is set to 1×10-3. The atom-adding threshold and the atom-deleting threshold have wide choices to get similar good results, and here we set 0.4 and 0.6 as suggested in [30]. In order to demonstrate the effectiveness of the JSRC method using multiple AE sensors for the rub-impact classification, we also compare it with the SRC method using AE signal from a single AE senor. Moreover, a modified SVM classifier named concatenated SVM (CSVM) [11], concatenating the cepstral features of all AE measurements into a single vector as the input for the SVM, is also used for comparison. For each class 10 rounds 3-fold-cross-validation are used as the evaluation type and the average performances are reported in Table 1.
Table 1The classification accuracy of the rub-impact in rotating machinery (noted as ‘%’)
Method | Non | Medium | Heavy |
JSRC-BSOMP | 98.87 | 91.28 | 94.58 |
JSRC-SOMP | 98.76 | 90.06 | 94.16 |
CSVM | 93.87 | 84.78 | 90.46 |
SRC-A | 95.42 | 86.63 | 92.58 |
SRC-B | 93.79 | 85.32 | 91.14 |
SRC-C | 93.56 | 85.28 | 90.79 |
SRC-D | 93.23 | 83.87 | 88.64 |
It is drawn from Table 1 that, the JSRC method obtains better classification results than the SRC method which demonstrates the advantage of jointly using the information from multiple AE sensors over only using the information from a single sensor or directly concatenating the information from multiple AE sensors. Moreover, the classification accuracy of the proposed JSRC-BSOMP method is better than the JSRC-SOMP method. For the non-rub-impact event all the methods can get good classification accuracies, while the JSRC method performances best. The classification accuracy for the medium rub-impact is lower than the heavy rub-impact, due to the fact that the medium rub-impact may be misclassified into non-rub-impact or heavy rub-impact. For the SRC method with a single AE sensor, the classification accuracy becomes lower and lower form senor A to senor D because of the distance to the AE source getting farther and farther, which is coincident with the early analysis in paper [4].
Fig. 3The classification accuracies with various values of sparsity
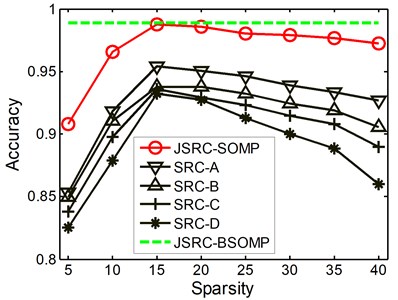
a) Non-rub-impact
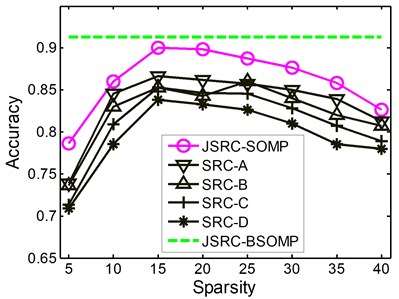
b) Medium rub-impact
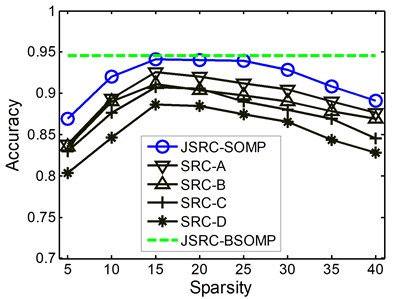
c) Heavy rub-impact
Further, in order to show the advantages of the BSOMP algorithm, we also investigate the effects of the parameter and namely the sparsity on the classification accuracies of the JSRC-SOMP and the SRC methods. The performances of two methods with the sparsity within the range {5, 10, 15, 20, 25, 30, 35, 40} are showed in Fig. 3 for all the three rub-impact events. It is drawn from Fig. 3 that, the classification performances of the JSRC-SOMP and the SRC vary heavily with the sparsity which demonstrates the advantages of the proposed BSOMP algorithm. The accuracy performances of the JSRC-SOMP and the SRC methods first increase with increased sparsity, and then get the leading classification accuracy around the sparsity of 15. This is the reason for which we set and to 15 for fair comparison. The classification performances decease when the sparsity goes beyond 25 which mainly because more atoms of the training dictionary from the incorrect classes are selected with the sparsity increasing thus deteriorating the classification performance. However, with the backtracking strategy the BSOMP algorithm could delete the incorrectly selected atoms, thus obtain the leading performance without the prior knowledge of the sparsity.
6. Conclusions
Inspired by the success of the joint sparse representation based classification (JSCR) method for the multiple measurements classification problem, in this paper we investigate the use of multiple acoustic emission (AE) sensors for the classification of rub-impact in rotating machinery. With the extracted cepstral coefficients of each AE sensor concatenated as the input matrix, the BSOMP algorithm is used to solve the JSRC problem to get the classification result. Experimental results demonstrate that the JSRC method with multiple AE sensors has higher rub-impact classification rate when compared to the SRC method with a single AE sensor. The proposed BSOMP algorithm is more flexible and better than the traditional SOMP algorithm for solving the JSRC method. In our future work, it is expected to employ a learned discriminative dictionary of the training data, in order to further improve the classification accuracy.
References
-
Ehrich F. F. Some observations of chaotic vibration phenomena in high-speed rotor dynamics. Journal of Vibration and Acoustics, Vol. 113, Issue 1, 1991, p. 50-57.
-
Aggelis D. G. Classification of cracking mode in concrete by acoustic emission parameters. Mechanics Research Communications, Vol. 38, Issue 3, 2011, p. 153-157.
-
Dunegan H. L. Modal analysis of acoustic emission signals. Journal of Acoustic Emission, Vol. 15, 1997, p. 53-61.
-
Deng A., Zhao L., Zhao Y. Recognition of acoustic emission signal based on mae and propagation theory. IEEE International Conference on Management and Service Science, 2009, p. 1-4.
-
Reynolds D., Rose R. C. Robust text-independent speaker identification using Gaussian mixture speaker models. IEEE Transactions on Speech and Audio Processing, Vol. 3, Issue 1, 1995, p. 72-83.
-
Deng A., Bao Y., Zhao L. Rub-impact acoustic emission signal recognition of rotating machinery based on Gaussian mixture model. Journal of Mechanical Engineering, Vol. 46, Issue 15, 2010, p. 52-58.
-
Deng A., Gao W., Bao Y., et al. Study on recognition characteristics of acoustic emission based on fractal dimension. IEEE International Conference on Embedded Software and Systems Symposia, 2008, p. 475-478.
-
Wright J., Yang A. Y., Ganesh A., et al. Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 31, Issue 2, 2009, p. 210-227.
-
Chakraborty S., Chatterjee A., Goswami S. K. A sparse representation based approach for recognition of power system transients. Engineering Applications of Artificial Intelligence, Vol. 30, 2014, p. 137-144.
-
Chen Y, Nasrabadi N M, Tran T D. Hyperspectral image classification via kernel sparse representation. IEEE Transactions on Geoscience and Remote sensing, Vol. 51, Issue 1, 2013, p. 217-231.
-
Zhang H., Zhang Y., Nasrabadi N. M., et al. Joint-Structured-Sparsity-Based Classification for Multiple-Measurement Transient Acoustic Signals. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), Vol. 42, Issue 6, 2012, p. 1586-1598.
-
Shekhar S., Patel V. M., Nasrabadi N. M., et al. Joint sparse representation for robust multimodal biometrics recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 36, Issue 1, 2014, p. 113-126.
-
Zhang E., Zhang X., Liu H., et al. Fast multifeature joint sparse representation for hyperspectral image classification. IEEE Geoscience and Remote Sensing Letters, Vol. 12, Issue 7, 2015, p. 1397-1401.
-
Mo X., Monga V., Bala R., et al. Adaptive sparse representations for video anomaly detection. IEEE Transactions on Circuits and Systems for Video Technology, Vol. 24, Issue 4, 2014, p. 631-645.
-
Jeon C., Monga V., Srinivas U. A Greedy Pursuit Approach to Classification Using Multitask Multivariate Sparse Representations. Technical Report PSUEE-TR-0112, Pennsylvania State University, PA, USA, 2012.
-
Tropp J. A., Gilbert A. C., Strauss M. J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Processing, Vol. 86, Issue 3, 2006, p. 572-588.
-
Huang H., Makur A. Backtracking-based matching pursuit method for sparse signal reconstruction. IEEE Signal Processing Letters, Vol. 18, Issue 7, 2011, p. 391-394.
-
Donoho D. L. Compressed sensing. IEEE Transactions on Information Theory, Vol. 52, Issue 4, 2006, p. 1289-1306.
-
Candès E. J., Romberg J., Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, Vol. 52, Issue 2, 2006, p. 489-509.
-
Donoho D. L., Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization. Proceedings of the National Academy of Sciences, Vol. 100, Issue 5, 2003, p. 2197-2202.
-
Wright J., Ma Y., Mairal J., et al. Sparse representation for computer vision and pattern recognition. Proceedings of the IEEE, Vol. 98, Issue 6, 2010, p. 1031-1044.
-
Donoho D. L. For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution. Communications on Pure and Applied Mathematics, Vol. 59, Issue 6, 2006, p. 797-829.
-
Tropp J. A., Gilbert A. C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, Vol. 53, Issue 12, 2007, p. 4655-4666.
-
Donoho D. L., Tsaig Y., Drori I., et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Transactions on Information Theory, Vol. 58, Issue 2, 2012, p. 1094-1121.
-
Needell D., Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Foundations of Computational Mathematics, Vol. 9, Issue 3, 2009, p. 317-334.
-
Needell D., Tropp J. A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Applied and Computational Harmonic Analysis, Vol. 26, Issue 3, 2009, p. 301-321.
-
Chen S. S., Donoho D. L., Saunders M. A. Atomic decomposition by basis pursuit. SIAM Review, Vol. 43, Issue 1, 2001, p. 129-159.
-
Lu W., Vaswani N. Regularized modified BPDN for noisy sparse reconstruction with partial erroneous support and signal value knowledge. IEEE Transactions on Signal Processing, Vol. 60, Issue 1, 2012, p. 182-196.
-
Tropp J. A. Algorithms for simultaneous sparse approximation. Part II: Convex relaxation. Signal Processing, Vol. 86, Issue 3, 2006, p. 589-602.
-
Van Den Berg E., Friedlander M. P. Theoretical and empirical results for recovery from multiple measurements. IEEE Transactions on Information Theory, Vol. 56, Issue 5, 2010, p. 2516-2527.
About this article
Wei Peng performed the data analyses and wrote the manuscript. Jing Li contributed to the conception of the study and the submission. Weidong Liu and Han Li contributed significantly to analysis and manuscript preparation. Liping Shi helped perform the analysis with constructive discussions
