Abstract
The static compression test of metal rubber components was carried out by using the control variable method. Influences of technological parameters such as relative density and metal wire diameter as well as structural parameters such as height and bearing area on mechanical properties of metal rubber material were studied. Based on micro-element infinitesimal spring theory, one-dimensional (1D) constitutive model of metal rubber material bearing compressive load was established, and it was found by comparing with experimental data that the curve fitted well and the model was reliable, could accurately describe the mechanical behaviors of metal rubber component when bearing load. The model provides theoretical basis for further study of mechanical properties of metal rubber material. It also guides design and manufacture of metal rubber products as well as its engineering application.
1. Introduction
With the development of science and technology, a great number of mechanical equipment have been applied to all aspects of engineering practice, vibration problems become increasingly prominent. Metal rubber (MR), a new type of functional material, is made from fine wire through certain technologies, and its internal structures are interrelated and interlaced so as to form spatial net link structure similar to ordinary rubber materials [1]. When fine wire goes through deformation under external load, friction, slippage, deformation and extrusion happen between spiral wire tunes, the generated dry friction between metal wires dissipate a large quantity of energy and exert effects of vibration attenuation and buffering. Metal rubber material has favorable elasticity like ordinary rubber material, greater damping capacity and shock absorption capacity, besides, it is non-volatile in vacuum and not afraid of radiation environment, with high and low temperature resistance, corrosion resistance and long service life [2].
In recent years, scholars have carried out in-depth researches on metal rubber material properties and achieved certain results [3-7]. However, these achievements only focused on the influence of variables on metal rubber material properties rather than the relationship between the mechanical properties of metal rubber material with its structural parameters and technological parameters. Li Yuyan based on porous material theory, established a nonlinear constitutive relation of metal rubber materials [8, 9]. Li Yuming combined the equivalent viscous damping theory and experimental experiment to build a dynamic model of metal rubber material, and deduced a meso-mechanical model of metal rubber material stress-strain relationship [10]. Peng Wei et al, based on micro-spring combined deformation theory, analyzed deformation rules of micro springs along the axial and radial directions and built a meso-constitutive model of metal rubber material [11]. Cao Fengli imported cantilever curved beam related to length and deformation history to characterize the meso-structure of metal rubber material [12, 13]. These models can describe stress-strain relationship of metal rubber material under compressive load, but they have too many correction coefficients with indefinite physical significance. Therefore, deformation characteristics of metal rubber material need to be further explored, as well as the constitutive model with higher precision, which is significant value to engineering application of metal rubber materials in the future.
Through compression experiment, a study of nonlinear mechanical properties of metal rubber was carried out in this paper, and then control variable method was used to conduct an analytical comparison among influences of relative density, metal wire diameter, diameter of metal spiral coil and bearing area on its compressive mechanical properties. According to small curved beam stressing model, infinitesimal spring theory was combined to build an 1D constitutive relation of metal rubber materials and compare it with the experimental results.
2. Metal rubber samples and experimental equipment
2.1. Metal rubber materials for test
Raw materials in preparation of metal rubber samples generally use austenitic stainless steel wire. Austenitic stainless steel has high plasticity and tenacity under normal temperature or low temperature and its processing performance is far superior to other types of stainless steel. Samples in this experiment adopted 304 (6Cr19Ni10) stainless steel, a kind of Cr-Ni stainless steel with extensive application. Physical property parameters of 304 steel were as shown in Table 1.
Table 1Physical property parameters of 304 (06Cr19Ni10) stainless steel
Ultimate strength / MPa | Yield strength / MPa | Elongation rate / % | Percentage reduction of area / % | Hardness |
≥ 520 | ≥ 205 | ≥ 40 | ≥ 60 | ≥ 187HBS; ≥ 90HRB; ≥ 200HV |
2.2. Preparation of metal rubber samples
Semi-automatic spiral coils with mandrel were used to wind the equipment to fabricate metal wire spiral coils with needed diameter, and its principle was as shown in Fig. 1. Equal-pitch stretching was conducted on these fabricated metal wire spiral coils so as to ensure mutual hooking between the metal wire spiral coils and good structural stability, then they were winded on the mould to make workblank, and the mould should be specially designed according to the planned shape and size of metal rubber samples [14]. Finally. these samples were made by cold press molding. Cold press molding equipment was as shown in Fig. 2.
Fig. 1Winding principle of semi-automatic spiral coils with mandrel
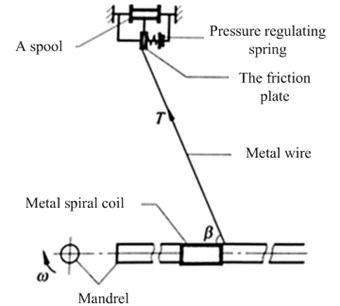
Fig. 2Cold press molding equipment

Basic dimensions of metal rubber samples required in this paper were: outer diameter 58.6 mm, inner diameter 41 mm and height 15 mm as shown in Fig. 3. All samples were circular annular shapes, schematic diagram of metal rubber samples was as shown in Fig. 4, where is outer diameter, is inner diameter and is height. Control variable method was adopted in this experiment to prepare samples with different relative densities, metal wire diameters, diameters of spiral coils and heights and bearing areas on the condition that basic dimension was consistent, and specific parameters were shown in Table 2.
Fig. 3Metal rubber samples

Fig. 4Schematic diagram of metal rubber samples
Table 2Parameters of metal rubber samples
Sample No. | Relative density | Wire diameter / mm | Diameter of spiral coil / mm | Dimension / mm (××) | Mass / g | Molding pressure / kN |
1 | 0.26 | 0.1 | 1.7 | 58.6×41×15 | 41.3 | 75 |
2 | 0.26 | 0.15 | 1.7 | 58.6×41×15 | 41.3 | 92 |
3 | 0.26 | 0.3 | 1.7 | 58.6×41×15 | 41.3 | 75 |
4 | 0.32 | 0.15 | 1.7 | 58.6×41×15 | 51.6 | 130 |
5 | 0.38 | 0.15 | 1.7 | 58.6×41×15 | 62.0 | 200 |
6 | 0.38 | 0.3 | 2.2 | 58.6×41×15 | 62.0 | 120 |
7 | 0.38 | 0.3 | 3.0 | 58.6×41×15 | 62.0 | 128 |
8 | 0.38 | 0.3 | 3.5 | 58.6×41×15 | 62.0 | 135 |
9 | 0.44 | 0.15 | 1.7 | 58.6×41×15 | 72.3 | 250 |
10 | 0.26 | 0.15 | 1.7 | 58.6×41×25 | 68.8 | 84 |
11 | 0.26 | 0.15 | 1.7 | 58.6×41×30 | 82.6 | 95 |
12 | 0.32 | 0.15 | 1.7 | 51×33×15 | 44.53 | 120 |
13 | 0.32 | 0.15 | 1.7 | 31×18×15 | 18.8 | 50 |
2.3. Testing equipment
The equipment used in this paper was WDW-T200 microprocessor control electronic universal testing machine manufactured by Jinan Tianchen as shown in Fig. 5 [15]. The equipment was used to test the mechanical properties of metallic or non-metallic materials under tension-compression or bending, maximum test force was 200 kN, displacement resolution was 0.001 mm and displacement deviation was not greater than ±0.5 % [16].
Constant-speed displacement control pattern was used in this experiment to conduct displacement loading, and according to the requirements of static test, loading velocity was set as 1mm/min, displacement 3mm and schematic diagram of testing unit was as shown in Fig. 6.
Fig. 5Universal testing machine

Fig. 6Schematic diagram of testing unit
3. Testing results and analysis
To ensure operating stability of static force loading device and data reliability, two samples were fabricated in each group, and each sample was tested for three times, and then the average values were used for analytical study.
3.1. Influence of relative density
Relative density of metal rubber is the main parameter influencing the mechanical properties of metal rubber materials during preparation process, and the relative density is defined as:
where is the density of metal rubber sample and is the density of metal wire.
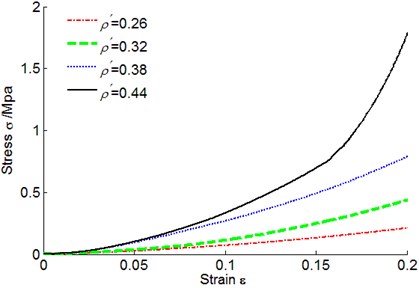
In order to make analytical study of the influence of relative density on nonlinear stiffness of metal rubber materials, under the circumstance that the other parameters were kept unchanged, samples with relative densities being 0.26, 0.32, 0.38 and 0.44 namely samples with sample No. being 2, 4, 5 and 9 in Table 2 were prepared, metal rubber samples were respectively conducted with static compression test on universal testing machine, and the metal rubber sample stress-strain curves under different densities were shown in Fig. 7.
It could be seen from the stress-strain curves that the compressive deformation of metal rubber materials was roughly divided into three phases: the first phase was the linear phase, this phase was shorter than other phases and it’s sometimes uneasy for it to appear in the image, when deformation was small, force presented linear growth trend as compressive displacement increased; the second phase was the soft characteristic phase also called the yield phase in which compressive load of metal rubber materials grew slowly and nonlinear characteristics became gradually obvious as the displacement increased; the third phase referred to the exponential hardening phase, when deformation reached a certain degree, compressive load presented exponential rising trend and its growth speed was continuously accelerated as deformation enlarged, because metal rubber was elastic porous material, when load was small, gap between metal wires was large, basically no relative slipping friction was generated between them, and stiffness roughly remained unchanged; when the applied load continued to be enlarged, metal wires contacted each other, thus gave rise to extrusion, extruding friction consumed energy, and consequently, damping increased; when extrusion between metal wires became more acute, stiffness continuously increased and accelerated speed increased, so stress-strain relation showed hardness characteristic.
Under the same deformation, the greater the relative density of metal rubber sample was, the greater the nonlinear elasticity modulus would be. Stiffness change rates of samples with different relative densities were also different. The sample with larger relative density, its stiffness increased faster and the hardness characteristic enhanced obviously, because on the condition that boundary dimensions were identical, the sample with larger relative density had smaller metal wire holes, closer arrangement of metal wires, more sufficient contact between them, more obvious extruding phenomenon, and the hardness characteristic effect was more prominent. Under the same load, as the relative density increased, the deformation quantity became smaller and smaller, and from a macroscopic view, bearing capacity of the sample with lager relative density was stronger.
Fig. 7Metal rubber stress-strain curves under different densities
3.2. Influence of metal wire diameter
Fig. 8 concerns the stress-strain curves of metal rubber components under different metal wire diameters which were respectively 0.1 mm, 0.15 mm and 0.3 mm, namely sample 1, 2 and 3 in Table 2. It could be seen from the figure that when the deformation changed little, samples with three different metal wire diameters had little difference in nonlinear elasticity modulus, being basically identical; however, when the deformation quantity exceeded a constant value, three samples started having a difference in nonlinear elasticity modulus, and under the same deformation, the greater the metal wire diameter of metal rubber samples, the smaller the corresponding load.
Fig. 8Metal rubber stress-strain curves under different diameters of metal wires
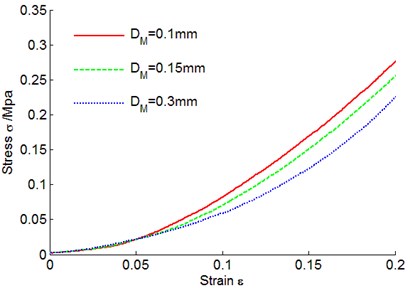
This phenomenon could be explained as: in initial deformation phase, metal wires inside metal rubber samples experienced contact-free deformation, so three samples has no obvious difference in stiffness; on the condition that other parameters were the same, as the deformation quantity increased, the component with smaller wire diameter had closer metal wire arrangement inside it, the greater the quantity of spiral coils, the stronger the extruding deformation, and the greater the stress change. Metal wire diameter mainly influenced stiffness of metal rubber materials in nonlinear phase, but had little effect on stiffness in linear phase. In engineering application, when the deformation of metal rubber component was in nonlinear phase, stress-bearing capacity could be improved by reducing metal wire diameter.
3.3. Influence of spiral coil diameter
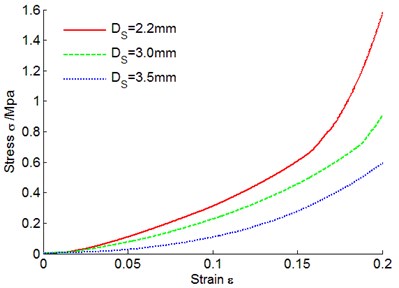
To study the influence of spiral coil diameter on nonlinear stiffness of metal rubber materials, sample 6, 7 and 8 were tested, and results were shown in Fig. 9.
It could be seen that similar to influence of metal wire diameter, the stiffness of samples with different spiral coil diameters had no obvious difference in initial deformation phase, as the deformation quantity increased, nonlinear elasticity modulus of metal rubber material reduced gradually. Because of enlargement of the spiral coil diameter, number of spiral coils inside a sample within unit volume reduced, so did their stiffness, and their hardness characteristics were not obvious. Hence, nonlinear elasticity modulus of metal rubber materials presented descending trend as spiral coil diameter increased, and its effect was mainly acted on the nonlinear phase.
Fig. 9Metal rubber stress-strain curves under different spiral coil diameters
3.4. Influence of sample height
Technological parameters of metal rubber samples 2, 10 and 11 were kept unchanged, inner and outer diameters as appearance parameters remained unchanged, only their heights were changed, and then their stress-strain curves were shown in Fig. 10. Under the same deformation, the sample with low height value bored greater stress, thus it could be seen that bearing capacity of metal rubber material was inversely proportional to its height. In engineering application, elevating bearing capacity of metal rubber product could appropriately reduce the height value of the component within the required scope.
3.5. Influence of bearing area
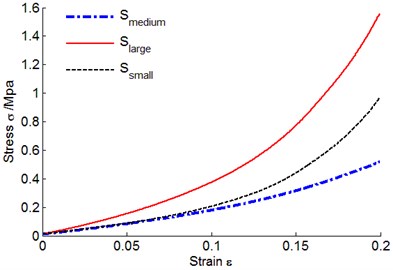
Samples with different bearing areas were compressed in the experiment, samples were numbered as 4, 12 and 13, and their stress-strain curves were shown in Fig. 11. Bearing capacity of metal rubber sample with larger bearing area was the best, followed by the intermediate model, and performance of sample with small bearing area was the poorest. Therefore, under the circumstance that other parameters were the same, increasing bearing area could improve bearing capacity of metal rubber sample and enhance vibration damping performance.
Fig. 10Metal rubber stress-strain curves under different heights
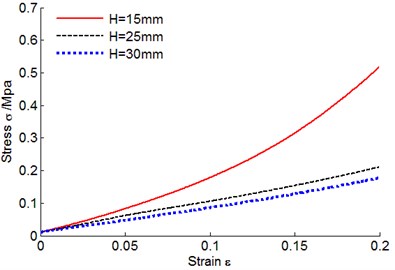
Fig. 11Metal rubber stress-strain curves under different bearing areas
4. Constitutive relation model of metal rubber material and its verification
4.1. Establishment of constitutive relation model of metal rubber under unidirectional compressive load
Metal rubber samples involved in this experiment were put under static compression test in their molding directions, so the studied constitutive model was established on this basis, and then stress-strain relations when they were compressed in molding directions were obtained. Metal rubber was made by stretching the winded metal spiral coils with equal thread pitch and then winding and pressing these coils, it could be basically deemed that metal wires were under parallel distribution on molding pressed surface. Model proposed in Literature [17]was established on the basis of small curved beam theory, relational expressions of basic parameters as needed in elasticity calculation of metal rubber materials were obtained to describe deformation of metal rubber materials. As shown in Fig. 12, direction was the molding pressed direction.
Fig. 12Stress-bearing graph of small curved beam inside metal Rubber
According to virtual work principle in mechanics of materials [18], energy needed by deformation of elastomer was equal to the work applied by the external force to it, namely:
where:
where is torque, is bending moment, is shear modulus, is polar moment of inertia.
According to small curved beam model, its bending moment and torque expressions were known and substituted into Eq. (3), and relationship between force and displacement could be obtained through Eq. (2):
was called stiffness coefficient of infinitesimal spring in pressing direction , where is the metal wire diameter, is the spiral coil diameter of metal wire, is the displacement in direction , is the elasticity modulus of metal wire, and is Poisson’s ratio. Infinitesimal model of metal rubber was shown in Fig. 13, it’s assumed that there were layers of springs on unit length and infinitesimal springs on unit area, and on each layer of infinitesimal springs, these springs were in parallel, and then total equivalent stiffness was:
Fig. 13Infinitesimal model of metal rubber
Mutual relations between springs from various layers were parallel, and then total equivalent stiffness is:
In fact, infinitesimal springs had different morphologies, so their stiffness coefficients were generally different, but from the perspective of statistics, there was certainly an intermediate average stiffness, and this intermediate average stiffness was regarded as stiffness coefficient of infinitesimal spring, then Eq. (5) and Eq. (6) were transformed into:
Then relational expression between force and displacement of metal rubber was:
Eq. (9) was constitutive relation of metal rubber within unit volume:
So, total number of spiral coils inside metal rubber with volume being was:
Number of spiral coils within unit volume was:
was the relative density mentioned above, and the following can be obtained through Eq. (12):
where , then:
Static compression experimental results of metal rubber samples indicated that their stress-strain relations presented nonlinear characteristics as strain (or deformation) increased, and as shown in results in section 2: infinitesimal springs of metal rubber were mutually winded and hooked, when deformation was small, deformation force was not enough to overcome static friction and presented effect of spring form, stress-strain curves were approximately linear, and when deformation gradually increased, relative slippage occurred between infinitesimal springs, which then reduced stiffness and gave rise to soft characteristics. When deformation quantity reached a certain degree, internal infinitesimal springs extruded each other, thus changing their original state and making them lose part of elasticity, and even some springs experienced failure, and they presented exponential characteristics on stress-strain curves. According to the test and above analysis, constitutive relational Eq. (14) of metal rubber materials was corrected: linear function of stress-strain of linear model was corrected into cubic curve of strain, namely:
where , and are constants and obtained through experiment.
Eq. (15) was the constitutive relation model of metal rubber materials bearing static compressive load which could directly reflect influences of basic parameters like metal wire diameter , relative density of metal rubber, spiral coil diameter and elasticity modulus of metal wire.
4.2. Testing verification of model
To verify correctness of the above constitutive relation model of metal rubber based on infinitesimal spring theory, data of sample 10 were taken to do model parameter identification, and the least squares method was used to fit coefficients of cubic polynomial. Obtained parameters through fitting were substituted into data of other samples for comparison. The comparison results between tested values and model theoretical calculating values were as shown in Fig. 14.
Fig. 14Comparison between model calculated value and tested value of mr samples
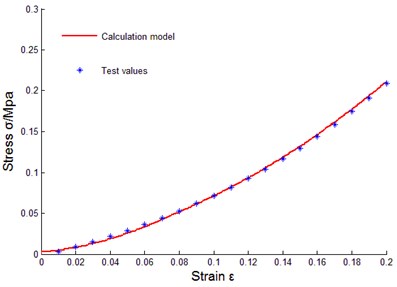
a) No. 1
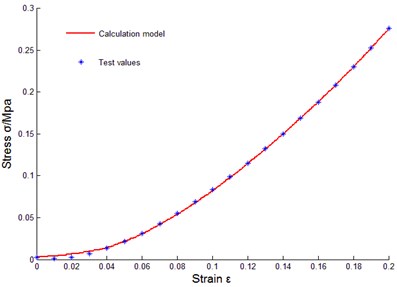
b) No. 2
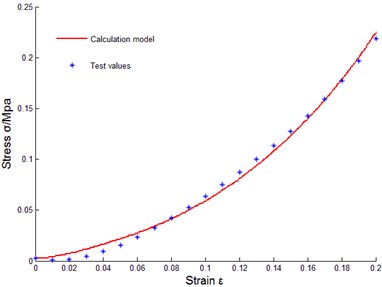
c) No. 3
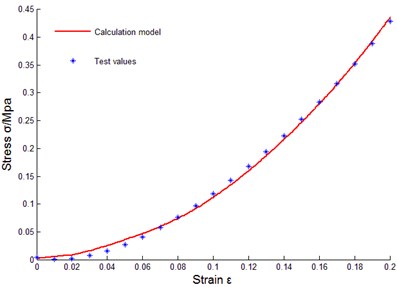
d) No. 4
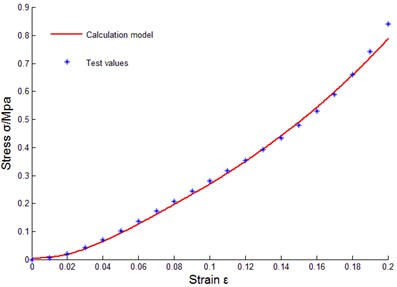
e) No. 5
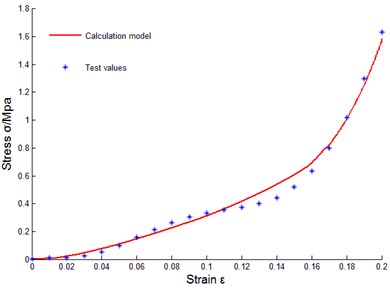
f) No. 6
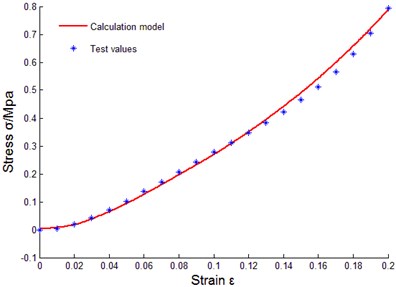
g) No. 7
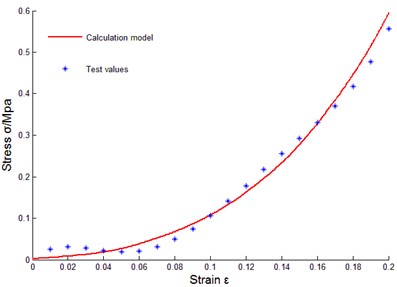
h) No. 8
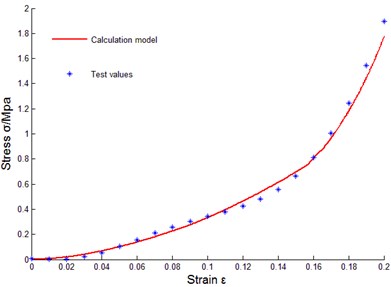
i) No. 9
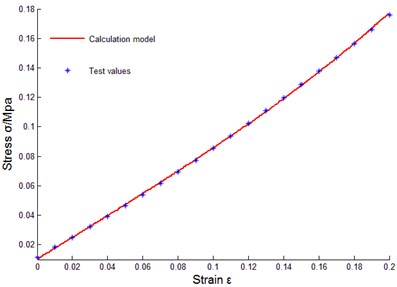
j) No. 11
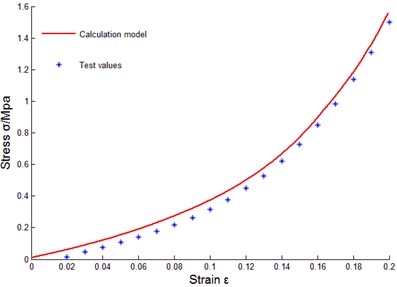
k) No. 12
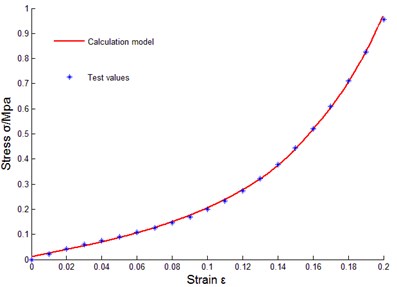
l) No. 13
Some curves did not match exactly, reasons for error were analyzed as: diameters of winded metal spiral coils could not be guaranteed as completely identical, and under cold press molding, uniformity of metal wire arrangement could not be ensured, in addition, initial conditions during testing process were not uniform, and therefore, certain errors existed between theoretical values and tested values of model of metal rubber component.
It could be seen that established constitutive relation model of metal rubber could describe variational relations between stress-strain under static load and relative density of metal rubber, metal wire diameter as well as spiral coil diameter very well, error between test curve and theoretical value was small, so the model could accurately describe the stiffness characteristic under static load. Therefore, improving various links in preparing process of metal rubber components in future work will be conductive to improving model accuracy and its engineering practicability.
5. Conclusions
Through static compression experiment on several groups of metal rubber samples, influences of relative density, metal wire diameter, spiral coil diameter, metal rubber sample height and bearing area on mechanical properties of metal rubber materials were compared, and results indicated that increasing relative density of metal rubber sample, reducing metal wire diameter, enlarging spiral coil diameter and reasonably selecting component height and bearing area could effectively improve the mechanical properties of metal rubber component. Constitutive relation model of metal rubber was established on the basis of infinitesimal spring theory, while curve fitting was implemented through the least squares method, and it was found by comparing with tested values that the adopted cubic polynomial could accurately describe mechanical behaviors of metal rubber samples under static compressive load and it described quantitative relationship between their stress-strain with technological parameters like relative density of metal rubber, metal wire diameter and spiral coil diameter and structural parameters like height and bearing area very well.
References
-
Chegodae D. The Design of Metallic Rubber Component. National Defence Industry Press, Beijing, 2000.
-
Bai Hongbai, Lu Chunhong, et al. Metal Rubber Material and Engineering Application. Science Press, Beijing, 2014.
-
Jiang Hongyuan, Yan Hui, Ao Hongrui, et al. Calculation of elastic damping characteristics of rotor support made of metal rubber material under variable load. Chinese Journal of Mechanical Engineering, Vol. 20, Issue 6, 2007, p. 33-37.
-
Ma Yanhong, Guo Baoting, Zhu Zigen Static characteristics of meter-rubber. Journal of Aerospace Power, Vol. 19, Issue 3, 2004, p. 326-331.
-
Li Shengbo, Yan Hui, Jiang Hongyuan, et al. Analysis of dynamic performance of metal rubber damping ring applied in high-speed rotor system. Acta Physica Sinica, Vol. 61, Issue 1, 2012, p. 10702-10702.
-
Li Yulong, He Zhongbo, Bai Hongbai, et al. Advances in research and application of metal rubber. Ordnance Material Science and Engineering, Vol. 1, 2011, p. 103-107, (in Chinese).
-
Fu Miguo, Liu Yuan, Cui Minliang, et al. Metal-rubber vibrator absorber for aerocraft. Optics and Precision Engineering, Vol. 21, Issue 5, 2013, p. 1174-1182.
-
Li Yuyan, Huang Xieqing Nonlinear stiffness of meta1-rubber. Acta Armamentarii, Vol. 29, Issue 7, 2008, p. 819-823.
-
Li Yuyan, Huang Xieqing Constitutive relation for metal-rubber with different density and shape factor. Acta Aeronautica et Astronautica Sinica, Vol. 29, Issue 4, 2008, p. 1084-1090, (in Chinese).
-
Li Yuming, Peng Wei, Bai Hongbai, et al. Mechanical model of metal rubber material in macro and micro level. Journal of Mechanical Engineering, Vol. 41, Issue 9, 2005, p. 38-41.
-
Peng Wei, Bai Hongbai, Zheng Jian, et al. A micromechanics constitutive model of the metal rubber materials based on the radial and axial combined deformation of the mircrosprings. Journal of Experimental Mechanics, Vol. 20, Issue 3, 2005, p. 455-462, (in Chinese).
-
Cao Fengli, Bai Hongbai, Ren Guoquan, et al. A constitutive model of metal rubber material based on curved cantilever beam of variable length. Journal of Mechanical Engineering, Vol. 48, Issue 24, 2012, p. 61-66.
-
Cao Fengli, Bai Hongbai, Li Dongwei, Al Research on Mechanical model of metal rubber for hysteresis characteristic in the non-forming direction. Journal of Mechanical Engineering, Vol. 51, Issue 2, 2015, p. 84-89.
-
Jiang Hongyuan, Ao Hongrui, Xia Yuhong, et al. Metal rubber molding technology research and its application. Mechanical Design and Manufacturing, Vol. 2, 2001, p. 85-86.
-
Wang Shulu The Design Theory and Experiment Research of Metal Rubber Vibration Isolator. Ordnance Engineering College, Shijiazhuang, 2016.
-
Li Dongwei The Reserach of Elasticity and Damping of Springy Coupling Based on Metal Rubber. Ordnance Engineering College, Shijiazhuang, 2003.
-
Deng Jianbo The Theoretical and Experimental Research on the Metal Rubber, A New kind of Structural Damping Materials. Beijing University of Aeronautics and Astonautics, Beijing, 1997.
-
Liu Hongwen Mechanics of Materials. Higher Education Press, Beijing, 2005.
